Capítulo 10 Introdução à distribuição das proporções amostrais e seus intervalos de confiança

A finalidade de uma amostra reside em obter uma estimativa do valor de um ou mais parâmetros associados a uma população. Verifica-se que, ao se extrair repetidamente valores amostrais de forma aleatória da mesma população, estes variam de uma amostra para outra, assim como em relação ao verdadeiro parâmetro dessa população. No entanto, é possível demonstrar que essa variabilidade pode ser caracterizada por meio de distribuições de probabilidade.

Quando utilizadas com esse propósito, essas distribuições de probabilidade são chamadas de distribuições amostrais. Elas permitem avaliar, para cada amostra, quão próximo está o valor da estatística amostral em relação ao verdadeiro parâmetro da população. A resposta a essa questão depende essencialmente de três fatores:

• A estatística específica que está sendo empregada: diferentes estatísticas demandam diferentes distribuições de probabilidade para modelar sua variabilidade.

• O tamanho da amostra, que exerce uma influência inversa na variabilidade entre os valores amostrais.

• A variabilidade intrínseca da população em estudo e do processo de amostragem.

10.1 Conceito elementar de uma proporção

O conceito básico de proporção remete à razão entre duas grandezas. Vejam os exemplos:

• segundo dados demográficos de 2012 (IBGE), a cidade de Recife possui proporcionalmente mais mulheres que homens;
  
• em 18 dias de campanha, somente 25,09% do público-alvo se vacinou contra gripe no País, segundo dados divulgados pelo Ministério da Saúde. De 17 de abril, quando a imunização foi iniciada, até 5 de maio, 13,6 milhões de brasileiros procuraram os postos de saúde para se vacinar.

Na primeira afirmação, a ideia de proporcionalidade advém do quociente do número habitantes do sexo feminino pelo numero total de habitantes naquele ano (\(\frac{827.885}{1.537.704}=0,5384\)). Já na segunda, a afirmação resulta do quociente do número de brasileiros vacinados pelo total da população-alvo (\(\frac{13.600.000}{54.200.000}=0,2509\)).

10.2 Distribuição das proporções amostrais

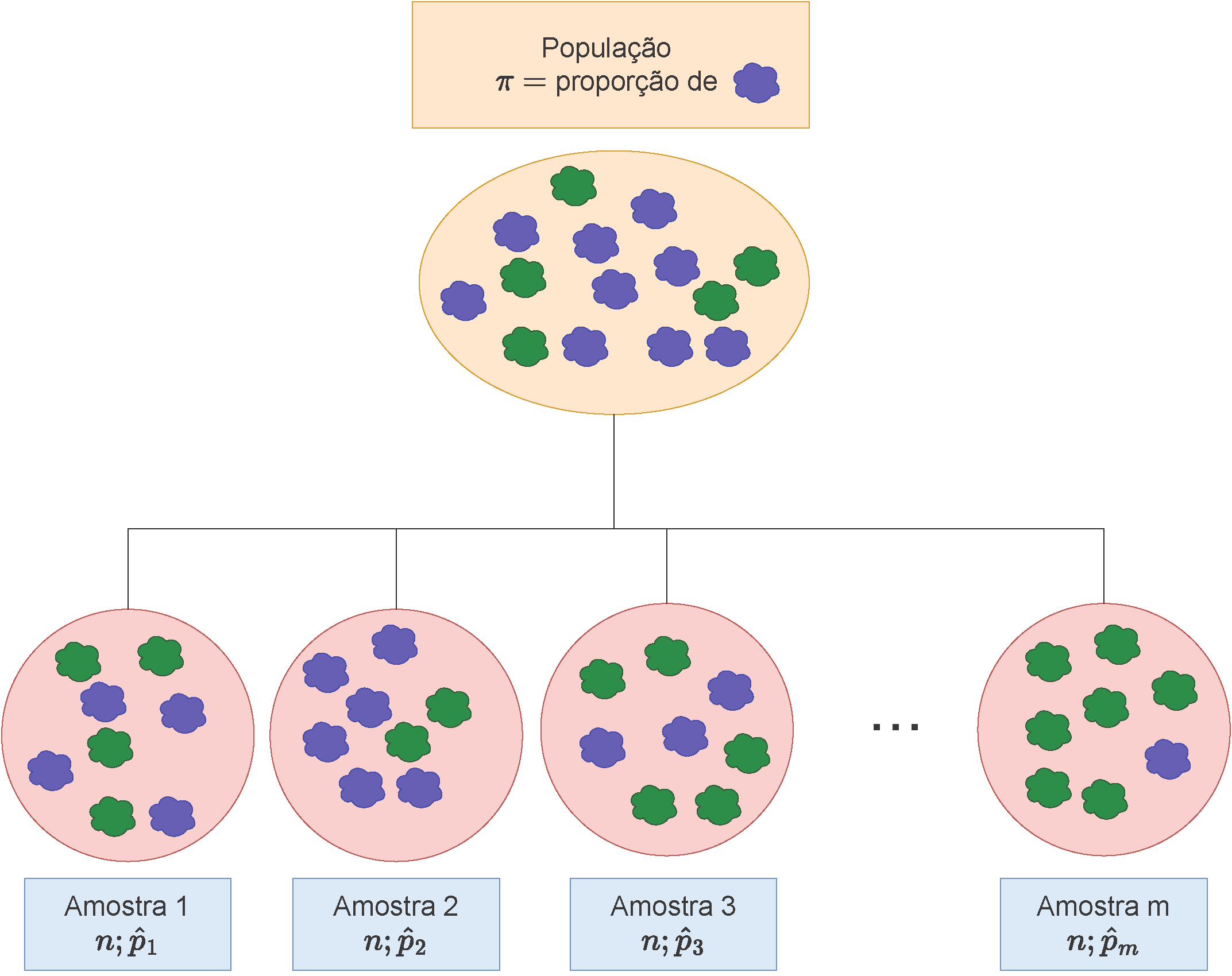
Figure 10.1: Ilustração de \(m\) amostras de mesmo tamanho (\(n\)) extraídas de uma mesma população onde a característica de interesse se manifesta sob uma proporção populacional \(\pi\)

Para estudarmos a distribuição das proporções amostrais (\(\hat{p}\)) considerem uma população apresentando uma determinada característica de interesse com proporção \(\pi\). Essa característica de interesse assume apenas duas possibilidades em cada elemento da população: ela pode ou não estar presente:

\[ X_{i}= \begin{cases} 1, \text{ se o i-ésimo elemento é portador da característica}\\ 0, \text{ se o i-ésimo elemento não é portador da característica}\\ \end{cases} \]

Assim, ao se escolher ao acaso um elemento da população, a probabilidade dessa característica estar presente pode ser estimada seguindo o modelo teórico de uma variável de Bernoulli e assim \(X_{i} \sim Ber(\pi)\) e, como tal, \(E(X)=\pi\) e \(Var(X)=\pi(1-\pi)\).

Repetindo-se essa ``extração’’ por \(n\) vezes podemos definir a variável aleatória \(Y_{n}\) como sendo o número de sucessos observados em \(n\) repetições de Bernoulli:

\[ Y_{n}= X_{1} + \dots + X_{n} \]

e assim, \(Y_{n} \sim Bin(n, \pi)\) e a proporção amostral observada de sucessos ao final das \(n\) repetições será a média:

\[ \hat{p}=\frac{Y}{n}=\frac{X_{1} + \dots + X_{n}}{n} \].

em que \(\hat{p}\) é uma estimativa amostral da proporção populacional \(\pi\).

Demonstra-se que para:

• um razoável número de repetições: \(n \ge 30\);
  
• de uma população onde a proporção \(\pi\) não é extrema: próximas a 0 ou 1; e tal que
• \((n \cdot \pi)\) e \((n \cdot (1-\pi))\) sejam maiores que 15 (alguns autores consideram limites mais brandos, iguais a 10 ou ainda a 5),

ao se repetir o experimento anotando-se as proporções amostrais \(\hat{p}\) obtida em cada uma das \(n\) repetições de Bernoulli , o perfil da curva de distribuição dessas proporções amostrais torna-se razoavelmente simétrico à medida que o número \(n\) de repetições de Bernoulli cresce, para qualquer que seja a proporção populacional, e oscila em torno de \(\pi\).

Pelo Teorema de DeMoivre e Laplace (anteriores ao Teorema do Limite Central), demonstra-se que, para um grande número de repetições (\(n\)), o valor esperado e a variância das proporções amostrais são:

\[\begin{align*} E(Y) & =n \cdot \pi \\ Var(Y) & =n \cdot \pi \cdot (1-\pi) \end{align*}\]

e a distribuição das proporções amostrais será aproximadamente Normal com parâmetros \(\mu=n.\pi\) e \(\sigma^{2}=n.\pi.(1-\pi)\):

\[ Y \sim N \left( n\cdot\pi ; n\cdot\pi\cdot(1-\pi) \right) \]

Uma vez que a proporção amostral está definida como: \(\hat{p} = \frac{Y_{n}}{n}\) segue-se que o valor esperado \(\hat{p}=\mu\):

\[\begin{align*} E(\hat{p}) & = E(\frac{Y}{n}) \\ & = \frac{1}{n} \cdot E(Y) \\ & = \frac{1}{n} \cdot n \cdot \pi \\ & = \pi \end{align*}\]

e a variância \(Var(\hat{p}=\frac{1}{n}.\pi.(1-\pi)\)):

\[\begin{align*} Var(\hat{p})& = Var(\frac{Y}{n}) \\ & = \frac{1}{n^{2}} \cdot Var(Y)\\ & = \frac{1}{n^{2}} \cdot n \cdot \pi \cdot (1-\pi)\\ & = \frac{1}{n} \cdot \pi \cdot (1-\pi ) \end{align*}\]

Assim, as proporções amostrais se distribuem de modo aproximadamente Normal sob uma média \(\mu=\pi\) e com uma variância \(\sigma^{2}=\frac{\pi \cdot (1- \pi)}{n}\):

\[ \hat{p} \sim N \left(\pi ; \frac{\pi \cdot (1- \pi) }{n} \right) \]

10.2.1 Simulações ilustrativas da aproximação da distribuição das proporções amostrais pela distribuição Normal

Para exemplificar considere o lançamento de um dado de seis faces,. A probabilidade de que uma certa face caia voltada para cima é de \(\frac{1}{6}=0,167\). Se lançarmos esse dado um número crescente de vezes e anotarmos a proporção delas em que a face escolhida caiu voltada para cima comprova-se que o valor esperado das proporções amostrais aproxima-se da proporção populacional.

As Figuras 10.2 (tamanho de cada amostra \(n=n_1\)) e 10.3 (tamanho de cada amostra \(n=n_2\)) mostram o perfil assumido pela distribuição de 100 proporções amostrais obtidas de uma população que apresenta uma proporção \(\pi=p_1\) da característica de interesse.

#############################################################################
# Considere uma população cuja característica de interesse (A) se manifesta de modo dicotômico:
# sim/não, sob uma probabilidade p_1 e (1-p_1).
# A probabilidade de se obter um elemento com a característica de interesse 
# - ao se sortear aleatoriamente um indivíduo qualquer - pode ser modelada como uma variável de Bernoulli.
# A probabilidade de se observar a característica de interesse ao se  
# repetir a amostragem (com reposição) por n_1 (n_2) vezes pode ser modelada como uma variável binomial (repetição de um experimento de Bernoulli n_1/n_2 vezes)   
# Repetindo-se esses experimentos binomiais por N vezes, as proporções amostrais de
# elementos com a característica de interesse (sucesso) nas N amostras obtidas será 
# dada pelo número de elementos de cada conjunto nas n_1 (n_2) repetições dividido por 
# n_1 (n_2).
# Desse modo, obtemos N proporções de amostras de tamanho n_1 (n_2)
#
#
# Selecionando-se aleatoriamente um elemento desta população 
# resulta em uma variável aleatória dicotômica/Bernoulli que assume 
# o valor 1 caso o elemento selecionado possua a propriedade A (sucesso)
# e assume o valor 0 caso não possua a propriedade A.
#
# A retirada (com reposição) de `n_1` elementos dessa população poderemos observar a frequência absoluta com que a propriedade A (sucesso) se manifesta na amostra, 
# a qual pode ser expressa  como uma variável aleatória (X) que segue o modelo teórico  Binomial de probabilidade. 
# 
# A frequência relativa, o quociente entre o número de sucessos por `n_1` expressa a 
# proporção com que a propriedade "A" foi observada na 'amostra' de tamanho `n_1` é também uma variável aleatória (p) com distribuição altamente relacionada à variável X  pois é a média de `n_1` ensaios (repetições) de Bernoulli.
#  
# Repetindo-se sucessivamente  `N` vezes extrações de tamanho `n_1` 
# a anotando-se a proporção de sucesso em cada uma dessas amostras poderemos analisar como eles se distribuem em relação à quantidade de elementos extraídos `n_1` (repetições de Bernoulli) 
# e à verdadeira proporção com que a propriedade A se manifesta na população (pi)  
#
# Demonstra-se que:
# para `n_1` suficientemente grande (repetições de Bernoulli com reposição);]
# n_1 * pi > 5 e 
# n_1*(1-pi) 5
# a distribuição de p pode ser aproximada pela distribuição Normal 
# tal que p ~N (mu,sigma)
# onde mu e sigma são aproximados por:
# mu = E(p) = pi
# sigma^2 = sigma^2*p >>>> sigma = sqrt[ p*(1-p)/(n_1)  ]
# 
#############################################################################

# Proporção escolhida para a manifestação da característica: sim/não (probabilidade de cada evento de Bernoulli)
p_1=round(1/6,2)

# Número de amostras
N=100             

# Tamanho escolhido para cada amostra: repetições de Bernoulli
n_1=10

# Vetor com o número de sucessos observados (a frequência absoluta) nas N amostras de n_1 elementos dicotômicos (repetições de Bernoulli, sob uma probabilidade individual de sucesso igual a p_1)

suc_10rep=rbinom(n=N, size = n_1, prob = p_1)
suc_10rep 

#  Vendo a proporção de sucessos (a frequência relativa) em cada uma das N_1 amostras de n_1 elementos dicotômicos
prop_10rep=suc_10rep/n_1
mean(prop_10rep) # ~ pi
sd(prop_10rep) # ~ sqrt(pi*(1-pi)/n_1)

# Dataframe com as N proporções amostrais sob n_1 
dados_10=as.data.frame(prop_10rep)

#############################################################################
# O mesmo procedimento, mas agora com amostras com um maior número de elementos em cada uma
#############################################################################

# Tamanho escolhido para cada amostra: repetições de Bernoulli
n_2=100

# Vetor com o número de sucessos observados (a frequência absoluta) nas N amostras de n_2 elementos dicotômicos (repetições de Bernoulli, sob uma probabilidade individual de sucesso igual a p_1)

suc_100rep=rbinom(n=N, size = n_2, prob = p_1)
suc_100rep 


#  Vendo a proporção de sucessos (a frequência relativa) em cada uma das N_1 amostras de n_1 elementos dicotômicos
prop_100rep=suc_100rep/n_2
mean(prop_100rep) # ~ pi
sd(prop_100rep) # ~ sqrt(pi*(1-pi)/n_2)

# Dataframe com as N proporções amostrais sob n_2 
dados_100=as.data.frame(prop_100rep)

meu_titulo1=paste("Distribuição de frequência das proporções de sucesso observadas em \n",N, "amostras de n=", n_1, "elementos dicotômicos extraídos (com reposição) da população","\n(proporção de sucesso na população \u03c0=", p_1,")")
meu_titulo2=paste("As proporções amostrais ~ \nN(\u03bc= \u03c0=",round(mean(dados_10$prop_10rep),3),";\u03c3 =sqrt(\u03c0*(1- \u03c0)/n)=",round(sd(dados_10$prop_10rep),3),")")


ggplot(dados_10, aes(x = prop_10rep)) + 
  geom_histogram(aes(y =..density..),
                 breaks = seq(0, 0.4, by = 0.05), 
                 colour = "black", 
                 fill = "lightblue") +
  stat_function(fun = dnorm, 
                args = list(mean = p_1, sd = sqrt(p_1*(1-p_1)/n_1)),
                 colour="red") +
  scale_y_continuous(name="",breaks = NULL) +
  scale_x_continuous(name="Valores das proporções amostrais") +
  #labs(title=meu_titulo1)+
  annotate(geom="text", x=mean(prop_10rep), y=max(dnorm(prop_10rep)),
           label=meu_titulo2, angle=0, vjust=0, hjust=0, color="blue",size=4)+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))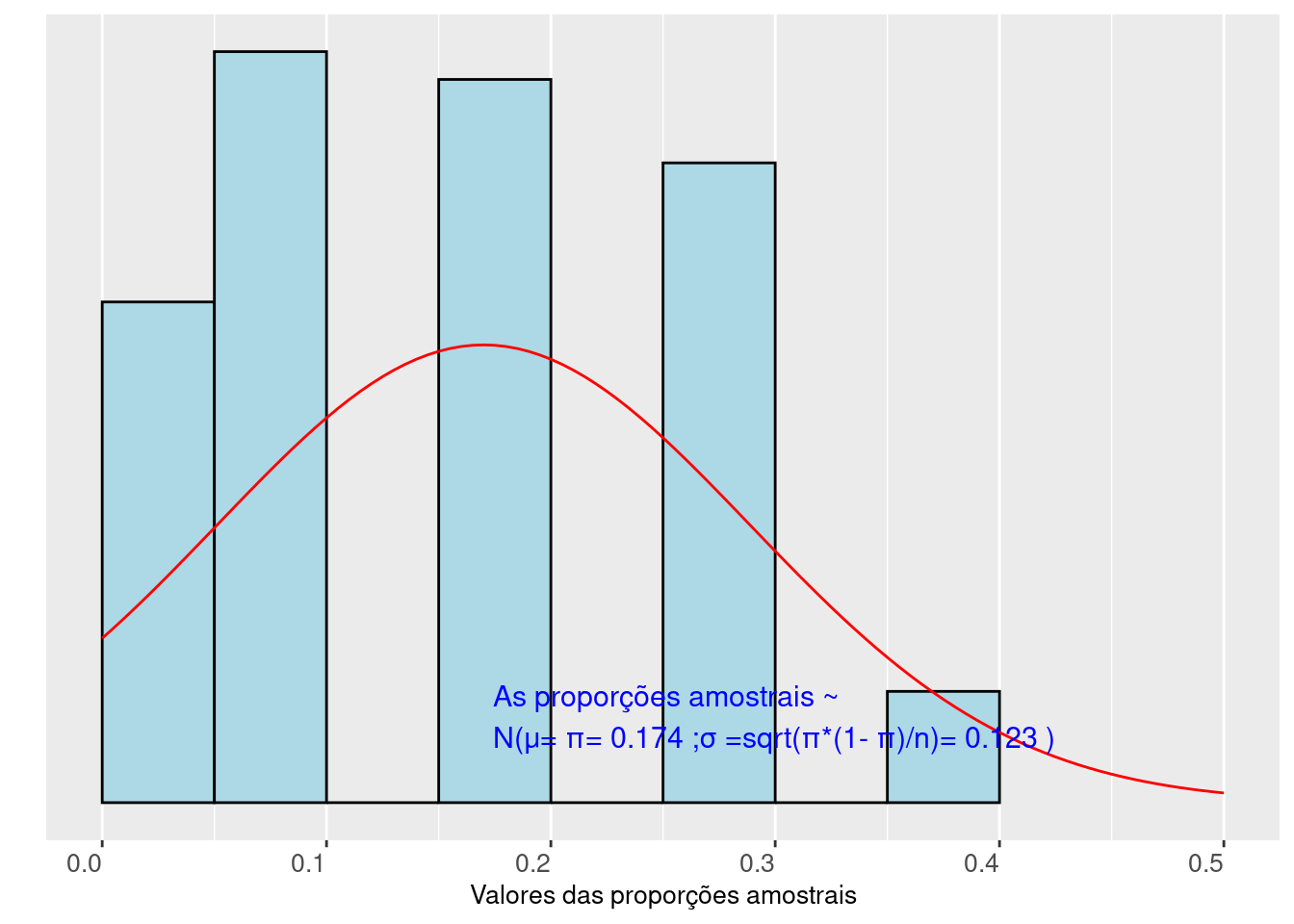

Figure 10.2: Distribuição das frequências das proporções de sucesso observadas em 100 amostras de tamanho n=10 elementos dicotômicos extraídos (com reposição) de uma população
(a proporção de sucesso na população é π=1/6)

meu_titulo1=paste("Distribuição de frequências das proporções de sucesso observadas em \n",N, "amostras de n=", n_2, "elementos dicotômicos extraídos (com reposição) da população","\n(proporção de sucesso na população \u03c0=", p_1,")")
meu_titulo2=paste("As proporções amostrais ~ \nN(\u03bc= \u03c0=",round(mean(dados_100$prop_100rep),3),";\u03c3=sqrt(\u03c0*(1- \u03c0)/n)=",round(sd(dados_100$prop_100rep),3),")")

ggplot(dados_100, aes(x = prop_100rep)) + 
  geom_histogram(aes(y =..density..),
                 breaks = seq(0, 0.4, by = 0.03), 
                 colour = "black", 
                 fill = "lightblue") +
  stat_function(fun = dnorm, 
                args = list(mean = p_1, 
                            sd = sqrt(p_1*(1-p_1)/n_2)), 
                colour="red") +
  scale_y_continuous(name="",breaks = NULL) +
  scale_x_continuous(name="Valores das proporções amostrais") +
  #labs(title=meu_titulo1)+
  annotate(geom="text", x=mean(prop_100rep), y=max(dnorm(prop_100rep)),
           label=meu_titulo2, angle=0, vjust=0, hjust=0, color="blue",size=4)+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))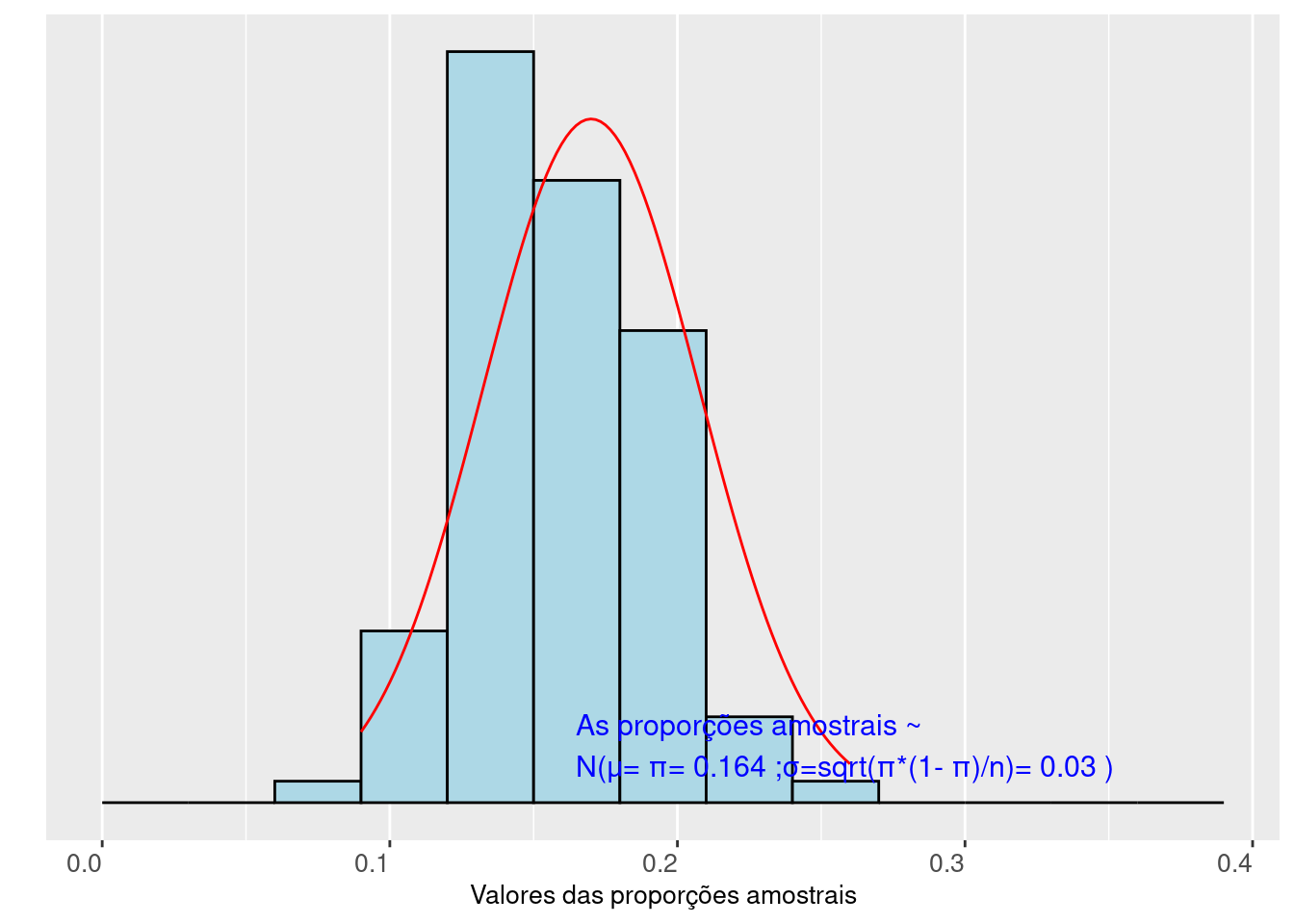

Figure 10.3: Distribuição das frequências das proporções de sucesso observadas em 100 amostras de tamanho n=100 elementos dicotômicos extraídos (com reposição) de uma população (a proporção de sucesso na população é π=1/6)

10.3 Pobabilidades associadas à observação de uma proporção amostral \(\hat{p}\)

Ao se definir a estatística \(Z\) como a simples padronização da variável \(\hat{p}\) vemos que esta seguirá uma distribuição normal com média \(0\) e desvio-padrão \(1\):

\[ Z=\frac{\hat{p}-\pi }{\sqrt{\frac{\pi \left(1-\pi \right)}{n}}} \sim N\left(0,1\right) \]

Essa aproximação da distribuição de uma variável binomial (proporções amostrais \(\hat{p}\)) pela distribuição Normal será tanto mais simétrica e com perfil de um sino quanto vier a atender (\(n\) grande e \(\pi\) não próximo de 0 ou 1) e nos permite determinar probabilidades associadas a proporções amostrais.

Exemplo: um sistema de produção opera de tal maneira que 10% das peças produzidas são defeituosas. Suponha que os itens sejam vendidos em caixas com 100 unidades e calcule as probabilidades de que em uma caixa: - tenha mais do que 10% de defeituosas? - tenha menos do que 15% de defeituosas?

Dados do problema: \(\pi=0,10\) e \(n=100\).

Considerando que a proporção populacional \(\pi\) não é extrema (próxima a 0 ou 1) e \((n \cdot \pi)\) e \((n \cdot (1-\pi))\) são maiores que 5, as proporções amostrais \(\hat{p}\) se distribuem, aproximadamente, do modo:

\[ \hat{p} \sim N \left(\mu: \pi ; \sigma^{2}: \frac{\pi \cdot (1- \pi) }{n} \right)\\ \hat{p} \sim N \left(0,10 ; \frac{0,10 \cdot (1- 0,10) }{100} \right)\\ \hat{p} \sim N (0,10; 0,0009) \]

Para se calcular as probabilidades de serem observadas proporções amostrais \(\hat{p}>0,10\) e \(\hat{p}<0,15\), basta-se mapear essas proporções amostrais à distribuição Normal padronizada. Assim, denotando-se uma variável aleatória (as proporções amostrais) \(X \sim n(\mu: 0,1; \sigma^{2}: 0,0009 (\sigma: 0,03))\) segue-se:

\[\begin{align*} P(\hat{p}> 0,10) & = P(X > 0,10 ) \\ & = P\left(\frac{X-0,10}{0,03} > \frac{0,10-0,10}{0,03}\right ) \\ & = P\left(Z >0 \right ) \\ & = 0,50 \end{align*}\]

e

\[\begin{align*} P(\hat{p} < 0,15) & = P(X < 0,15 ) \\ & = P\left(\frac{X-0,15}{0,03} < \frac{0,15-0,10}{0,03}\right ) \\ & = P\left(Z < 1,67\right ) \\ & = 0,9525 \end{align*}\]

10.4 A aleatoriedade das proporções amostrais e o tamanho amostral

No módulo ``Introdução ao planejamento de pesquisas’’ explicamos que quando não se dispõe de nenhuma informação a priori sobre a proporção populacional (\(\pi\)) a adoção do máximo valor possível ao produto: \(\pi.(1-\pi)=\frac{1}{4}\) assegura que o o tamanho de amostra obtido será suficiente para a estimação qualquer que seja a proporção populacional \(\pi\). Trazendo a variável \(Z\) antes definida:

\[ Z=\frac{\hat{p}-\pi }{\sqrt{\frac{\pi \left(1-\pi \right)}{n}}} \sim N\left(0,1\right) \]

podemos reescrevê-la de modo a se obter o dimensionamento amostral em função do nível de confiança e um erro máximo estabelecidos:

\[ z_{(1-\alpha)}=\frac{\hat{p}-\pi }{\sqrt{\frac{\pi \left(1-\pi \right)}{n}}} \\ z_{(1-\alpha)}.\sqrt{\frac{\pi \left(1-\pi \right)}{n}}=\hat{p}-\pi \\ \frac{\pi \left(1-\pi \right)}{n}=(\frac{\varepsilon}{z_{(1-\alpha)}})^{2}\\ n = \frac{z_{(1-\alpha)}^{2}}{\varepsilon^{2}} \cdot \pi \left(1-\pi \right)\\ \]

Deste modo podemos simular a flutuação dos valores das proporções obtidas em sucessivas amostras, ilustrando simultaneamente as proporções amostrais observadas e a proporção das amostras que apresentam um erro amostral (\(\varepsilon\)) superior ao estipulado pelo nível de confiança (\(1-\alpha\)).

Desconhecendo-se qualquer informação acerca da proporção populacional (\(\pi\)), a dimensão da amostra pode ser estipulada tomando-se o maior valor do produto \(\pi \left(1-\pi \right)\) como sendo igual a \(\frac{1}{4}\) pois:

p <- seq(0, 1, by = 0.01)
y <- p * (1 - p)
plot(p, y, type = "l", xlab = "\u03c0", ylab = "\u03c0*(1- \u03c0)", main = "Possíveis valores assumidos pelo produto: \u03c0*(1- \u03c0)")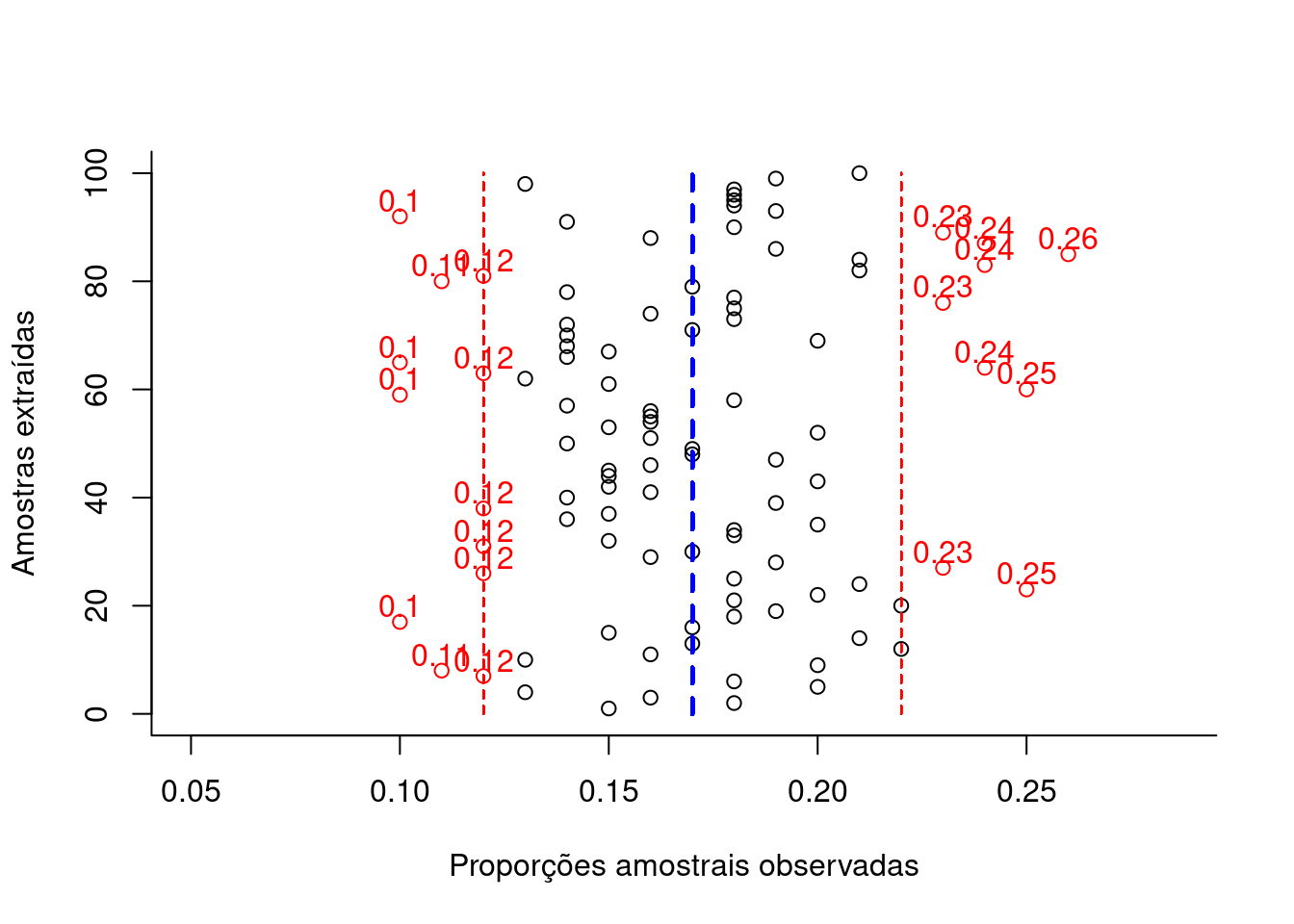

Figure 10.4: Possíveis valores assumidos pelo produto: π*(1- π)

Assim, a dimensão conservadora para a amostra será dada por:

\[ n = \frac{z_{(1-\alpha)}^{2}}{\varepsilon^{2}} \cdot \frac{1}{4}\\ \]

10.4.1 Simulações ilustrativas sobre as flutuações das proporções amostrais e o erro amostral fixado

As próximas figuras ilustram a flutuação das proporções amostrais obtidas de amostragens (com reposição) de elementos de uma população que apresentam a característica de interesse se manifestando de modo dicotômico, sob variados tamanhos amostrais (385, 210 e 100).

# Flutuação das proporções amostrais observadas

flut.N = function (N, n, p, conf, er) {
zc = qnorm(1-((1-conf)/2)) 
suc=rbinom(n=N, size = n, prob = p)
prop_suc=suc/n
dados=as.data.frame(prop_suc)
names=c("Proporção amostral")
colnames(dados)=names
row.names(dados)=NULL
meu_titulo01=paste0("Flutuação das proporções amostrais \n", N," amostras de tamanho ",n," (dimensionamento sob um nível de confiança (1-\u03b1)= ",conf," e um erro amostral \u03b5= ", er," \nAs linhas verticais mostram a propoção populacional em azul (\u03c0= ", p , ") \ne os valores limites estabelecidos pelo erro arbitrado em vermelho (\u03c0 +/-\u03b5= ",  p, "+/-", er ,")")   
meu_titulo02=paste0("Os valores das proporçoes amostrais seguem uma distribuição ~ N ( \u03bc, \u03c3) = (", round(mean(dados$`Proporção amostral`),4) ,", ", round(sqrt(p*(1-p)/n),4) ,")")


plot(0, 0, 
type="n", 
xlim=c( 0.5*min(dados$`Proporção amostral`) , 1.1*max(dados$`Proporção amostral`) ), 
ylim=c(0,N), 
bty="l",
xlab="Proporções amostrais observadas", 
ylab="Amostras extraídas", 
main="", #meu_titulo01  
sub="") #meu_titulo02

for (i in 1:N) {
prop_amostral=dados$`Proporção amostral`[i]
ploty = c(i,i)
if (prop_amostral > p+er || prop_amostral < p-er) 
     points(prop_amostral, i, col="red", cex=1)+text(y=i+3,x=prop_amostral, labels=round(prop_amostral,2), cex=1, col='red')
  else 
    points(prop_amostral, i, col="black", cex=1) 
segments(x0=p , y0=0, x1=p ,y1=N,col="blue", lwd=2, lty=2)
segments(x0=p-er , y0=0, x1=p-er ,y1=N,col="red", lwd=1, lty=2)
segments(x0=p+er , y0=0, x1=p+er ,y1=N,col="red", lwd=1, lty=2)
} 
}

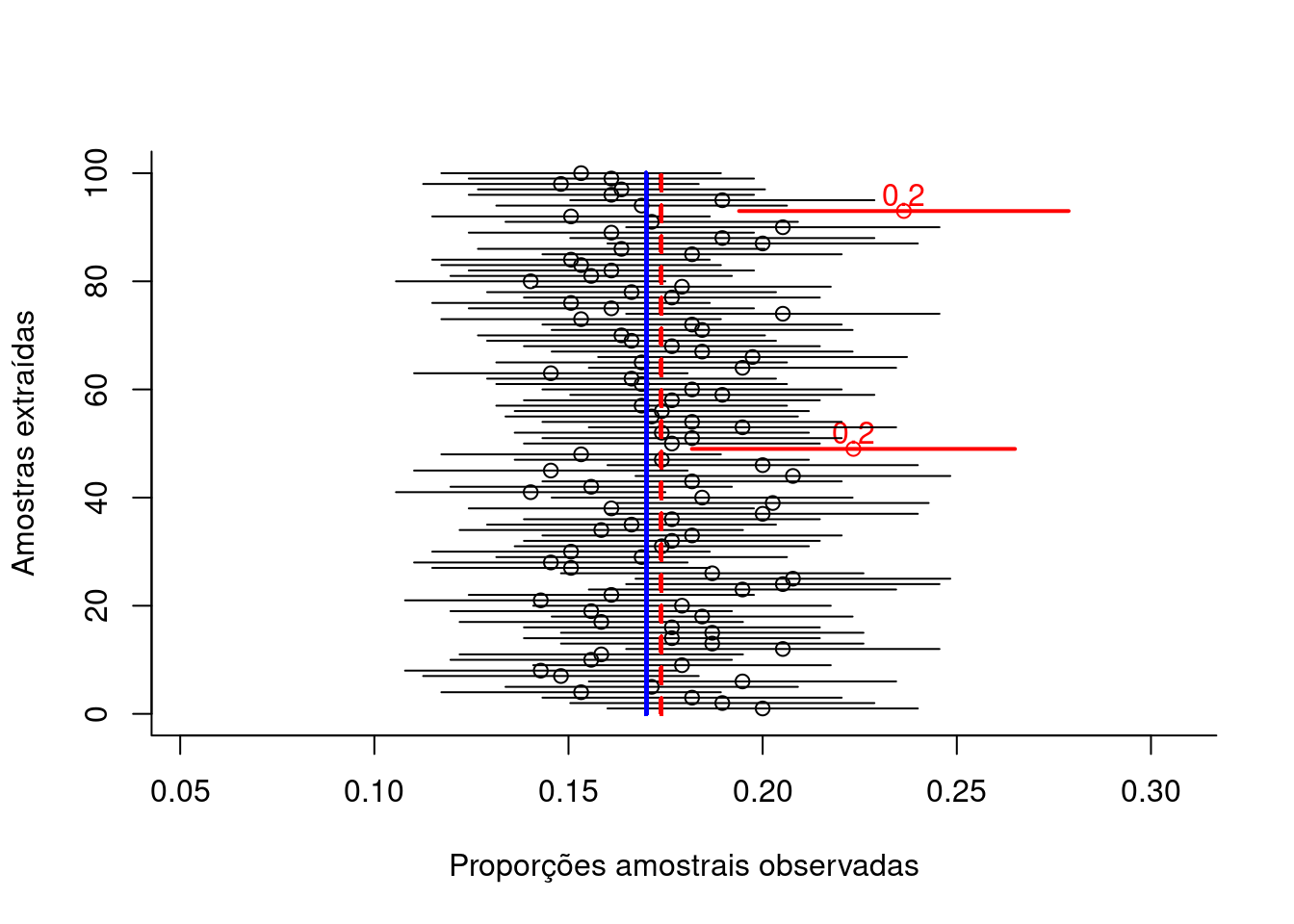
Figure 10.5: Flutuação das diversas proporções amostrais obtidas de amostragens cujo dimensionamento (385 elementos ) foi estimado ignorando-se o conhecimento da proporção populacional (π) para um nível de confiança (1-α)=0,95 e um erro amostral ε=0,05 (em preto as proporções amostrais dentro da tolerância fixada e, em vermelho, as que aleatoriamente ultrapassam a tolerância fixada em π +/-ε).

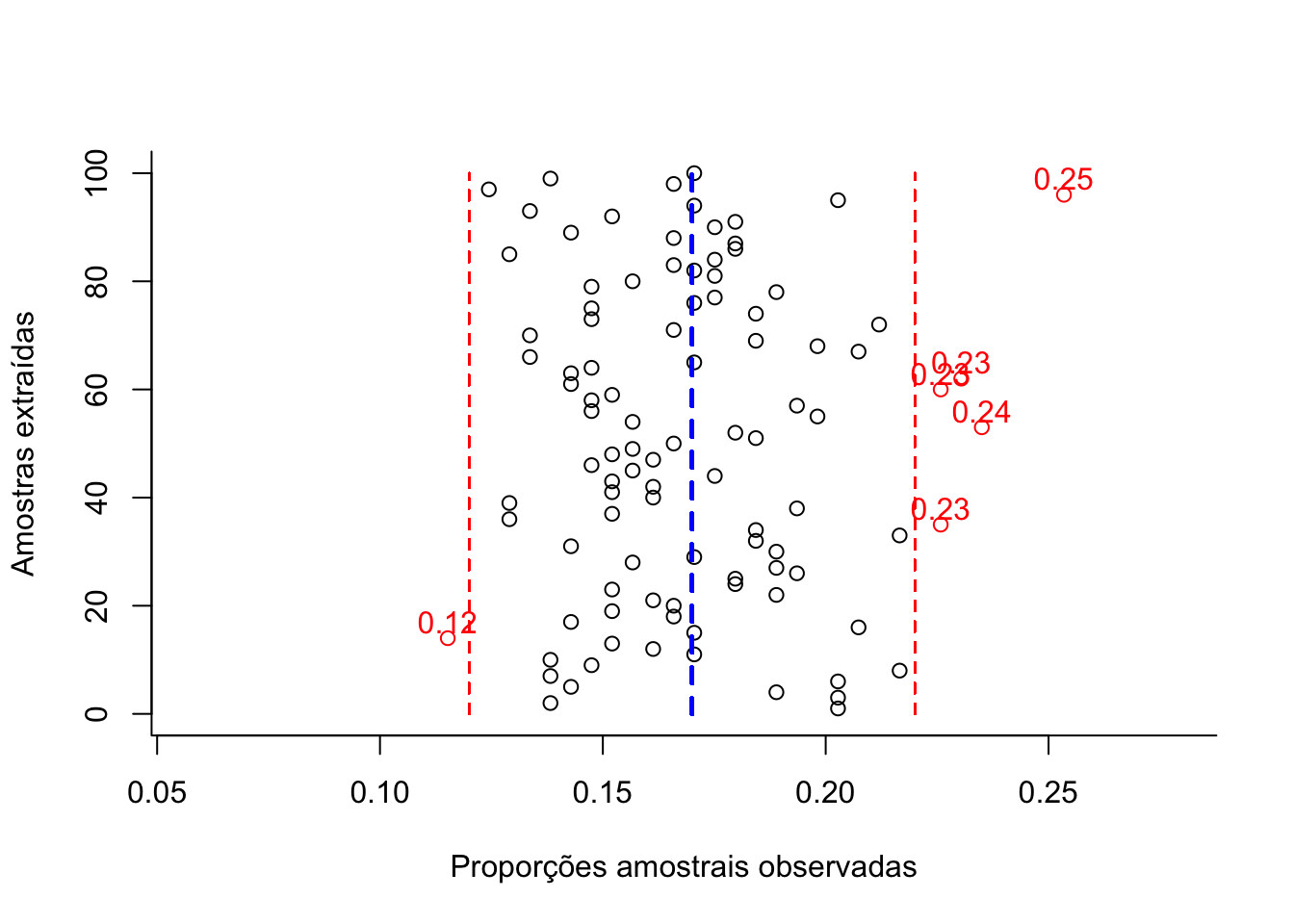
Figure 10.6: Flutuação das diversas proporções amostrais obtidas de amostragens cujo dimensionamento (217 elementos) foi estimado admitindo-se o conhecimento da proporção populacional (π) para um nível de confiança (1-α)=0,95 e um erro amostral ε=0,05 (em preto as proporções amostrais dentro da tolerância fixada e, em vermelho, as que aleatoriamente ultrapassam a tolerância fixada em π +/-ε).

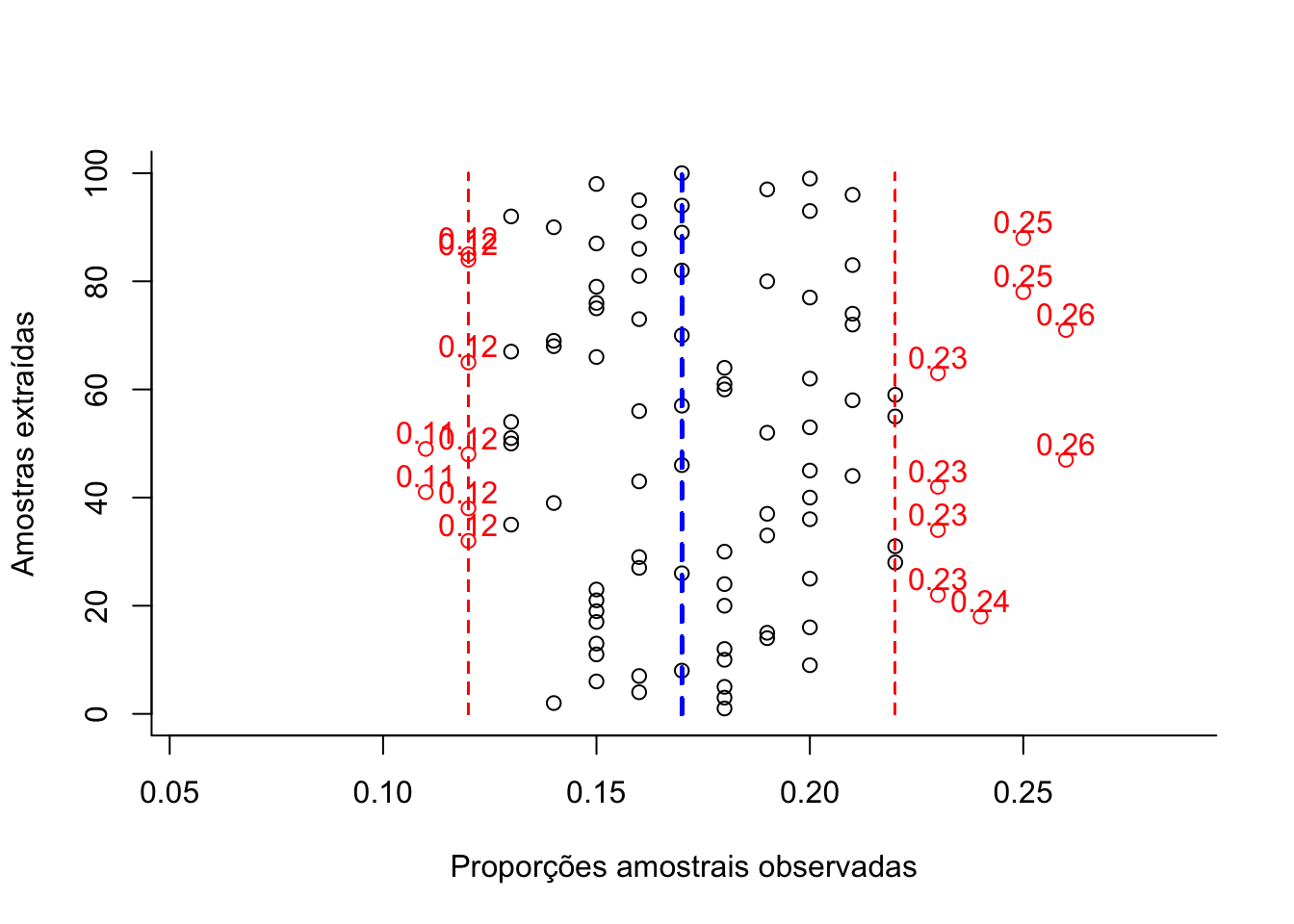
Figure 10.7: Flutuação das diversas proporções amostrais obtidas de amostragens cujo dimensionamento foi arbitrariamente fixado (100 elementos) para um nível de confiança (1-α)=0,95 e um erro amostral ε=0,05 (em preto as proporções amostrais dentro da tolerância fixada e, em vermelho, as que aleatoriamente ultrapassam a tolerância fixada em π +/-ε).

10.5 Intervalos de confiança para proporções amostrais

Podemos escrever o parâmetro (\(\pi\)) da proporção populacional em função da proporção amostral observada \(\hat{p}\) e de seu desvio padrão \(\sigma_{\hat{p}}\):

\[ Z=\frac{\hat{p}-\pi }{\sqrt{\frac{\pi \left(1-\pi \right)}{n}}} \sim N\left(0,1\right), \]

ou

\[ Z=\frac{\hat{p}-\pi }{{\sigma }_{\hat{p}}} \]

com \(Z \sim N\left(0,1\right)\).

Assim,

\[ \hat{p} - \pi = Z \cdot {\sigma }_{\hat{p}} \]

e

\[ \pi = \hat{p} + Z \cdot {\sigma }_{\hat{p}} \]

Observa-se, todavia, que a variância da distribuição Normal da aproximação da distribuição das proporções amostrais é expressa em termos do parâmetro da proporção populacional \(\pi\) que não é conhecido:

\[ \hat{p} \sim N [\pi ; \frac{\pi \cdot (1- \pi) }{n} ] \]

\[ {\sigma }_{\hat{p}}=\sqrt{\frac{\pi \left(1-\pi \right)}{n}}. \]

Demonstra-se que para:

• um razoável número de repetições: \(n \ge 30\);
  
• de uma população onde a proporção \(\pi\) não é extrema: próximas a 0 ou 1; e tal que
• \((n \cdot \pi)\) e \((n \cdot (1-\pi))\) sejam maiores que 15 (alguns autores consideram limites mais brandos, iguais a 10 ou ainda a 5),

Podemos tomar a proporção amostral \(\hat{p}\) como uma aproximação direta da proporção populacional \(\pi\) na expressão da variância da distribuição Normal que modela a distribuição das proporções amostrais sem que isso resulte em grande alteração na distribuição da variável \(Z\).

Ou ainda, alternativamente, fazendo-se antes uma aproximação com correção de continuidade, onde definimos uma nova estimativa amostral da proporção populacional \(\hat{p}_{c}\) corrigida:

\[ \hat{p}_{c} = \hat{p}+\frac{1}{2n} \]

se \(\hat{p} < 0,50\),

ou

\[ \hat{p}_{c} = \hat{p}- \frac{1}{2n} \]

se \(\hat{p} > 0,50\).

As probabilidades associadas aos valores assumidos pela variável \(Z \sim N\left(0,1\right)\): a área sob a curva, encontram-se tabelados e podem ser utilizados para construir intervalos de confiança para o parâmetro da proporção populacional \(\pi\) associados a probabilidades desejadas.

\[ P [ \hat{p} - Z \cdot {\sigma }_{\hat{p}} < \pi < \hat{p} + Z \cdot {\sigma }_{\hat{p}} ] = (1-\alpha) \]

Assim (com \(\hat{p}\) ou \(\hat{p}_{c}\)) podemos construir intervalos de confiança em torno da proporção populacional \(\pi\) associados a um nível de significância estabelecido:

Bilaterais: intervalo delimitado por dois valores: mínimo e máximo, para a proporção amostral, dentro do qual todos os valores possuem um mesmo nível de significância:

\[ P[\hat{p} - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} \hspace{0.1cm} \le \hspace{0.1cm} \pi \hspace{0.1cm} \le \hspace{0.1cm} \hat{p} + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1-\hat{p} \right)}{n}}] = (1-\alpha) \]

Unilaterais: intervalos delimitados apenas em um de seus lados nos quais todos os valores possuem um mesmo nível de significância:

• Valor máximo (limitando à direita):

\[ P[\pi \le \hat{p} + {z}_{\alpha} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} ] = (1- \alpha) \]

• Valor mínimo (limitando à esquerda):

\[ P [\pi \hspace{0.1cm} \ge \hat{p} - {z}_{\alpha} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} \hspace{0.1cm}] = (1-\alpha) \]

# Intervalos de confiança das proporções amostrais observadas

IC.N = function (N, n, p, conf, er) {
zc = qnorm(1-((1-conf)/2)) #Z=1,96  
suc=rbinom(n=N, size = n, prob = p)
prop_suc=suc/n
dados=as.data.frame(prop_suc)
dados$lim_sup=dados$prop_suc + zc*sqrt(dados$prop_suc*(1-dados$prop_suc)*(1/n))         
dados$lim_inf=dados$prop_suc - zc*sqrt(dados$prop_suc*(1-dados$prop_suc)*(1/n))   
names=c("Proporção amostral", "lim superior", "lim inferior")
colnames(dados)=names
row.names(dados)=NULL
meu_titulo001=paste0("Intervalos com iguais níveis de confiança fixados em ", 100*conf, "% \n(",N," amostras de tamanho ",n,") \nAs linhas verticais mostram a propoção populacional em azul (\u03c0: ", p , ") \ne a média das proporções amostrais em vermelho ( \u0070\u0302: ",round(mean(dados$`Proporção amostral`),4) , ").")
meu_titulo002=paste0("Parâmetros da distribuição da população Normal aproximada ( \u03bc, \u03c3) = (", round(mean(dados$`Proporção amostral`),4) ,", ", round(sqrt(p*(1-p)/n),4)     ,")")  



plot(0, 0, 
type="n", 
xlim=c( 0.5*min(dados$`lim inferior`) , 1.1*max(dados$`lim superior`) ), 
ylim=c(0,N), 
bty="l",
xlab="Proporções amostrais observadas", 
ylab="Amostras extraídas", 
main="", #meu_titulo001
sub="") #meu_titulo002

for (i in 1:N) {
prop_amostral=dados$`Proporção amostral`[i]
li = dados$`lim inferior`[i]
ls = dados$`lim superior`[i]
plotx = c(li,ls)
ploty = c(i,i)
if (li > p | ls < p) lines(plotx,ploty, col="red", lwd=2, lend=0)
  else lines(plotx,ploty, lend=0) 
    if (li > p | ls < p) points(prop_amostral, i, col="red", cex=1)+text(y=i+3,x=prop_amostral, labels=round(prop_amostral,1), cex=1, col='red')
      else points(prop_amostral, i, col="black", cex=1) 
segments(x0=mean(dados$`Proporção amostral`) , y0=0, x1=mean(dados$`Proporção amostral`) ,y1=N,col="red", lwd=2, lty=2)
segments(x0=p , y0=0, x1=p ,y1=N,col="blue", lwd=2, lty=1)
} 
}

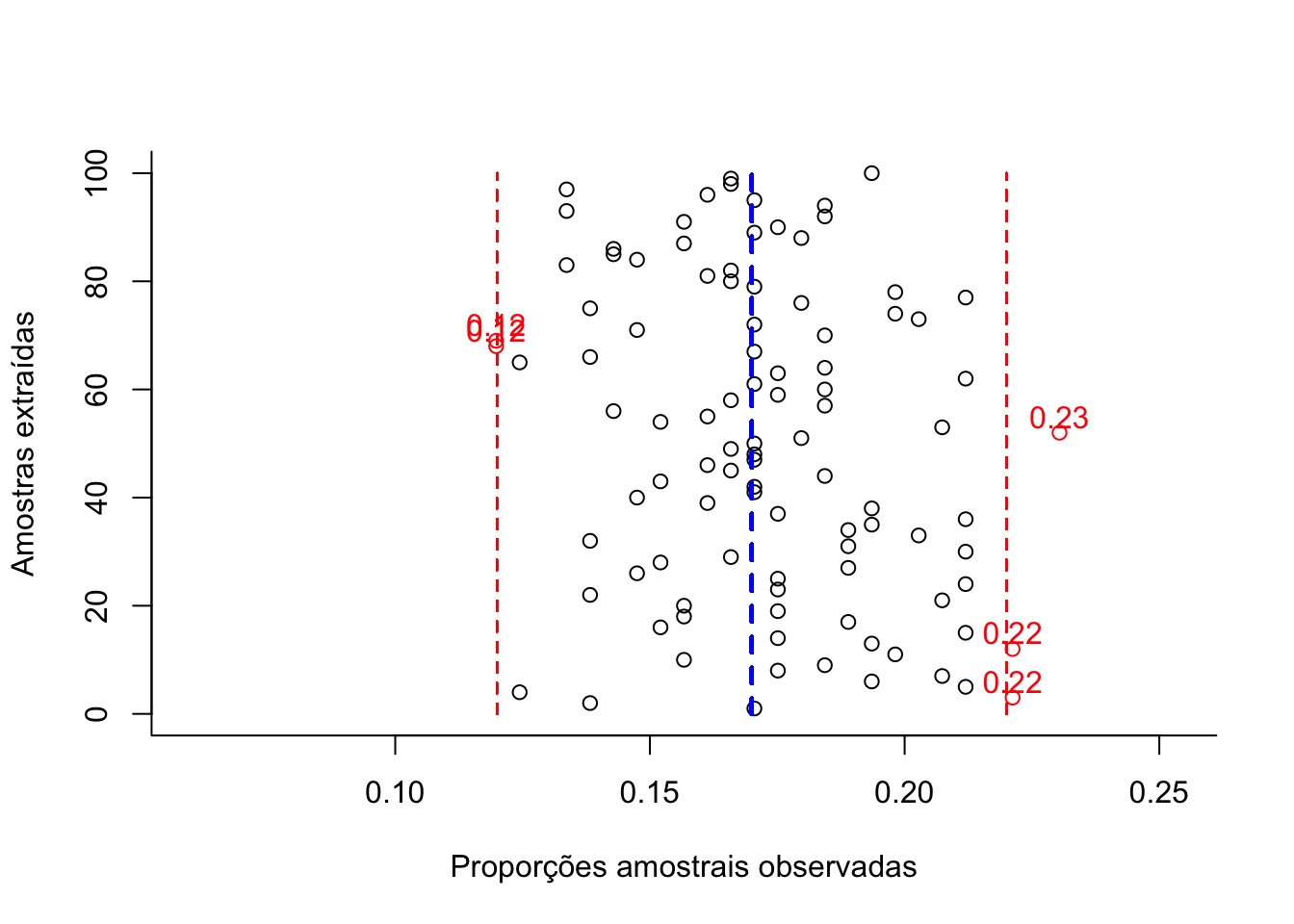
Figure 10.8: Intervalos de confiança construídos para as diversas proporções amostrais obtidas de amostragens (com reposição) de elementos de uma população que apresentam a característica de interesse se manifestando de modo dicotômico. O dimensionamento foi estimado ignorando-se o conhecimento da proporção populacional (π) para um nível de confiança (1-α) e um erro amostral (ε) estipulados: 385 elementos.

Exemplo: Em uma amostra aleatória, 136 pessoas de um grupo de 400 que receberam a vacina contra gripe, declararam haver sentido algum efeito colateral. Construa um intervalo com 95% de confiança para a verdadeira proporção populacional da ocorrência de efeitos colaterais vacinais .

Dados do problema:

• \(\hat{p}=\frac{136}{400}=0,34\) é a proporção amostral observada;
• o tamanho amostral (\(n=400\)) é grande e a proporção amostral (\(\hat{p}=0,34\)) não é extrema (próxima a zero ou um);
  
• \(\pi\) é a proporção populacional (desconhecida); e,
• para o nível de confiança solicitado (\((1-\alpha)=0,95\)) temos da tabela \({z}_{\left(\frac{\alpha }{2}\right)}= +/-1,96\).

Um intervalo bilateral (fechado) para a proporção populacional desconhecida (\(\pi\)) sob um nível de confiança (\(1-\alpha\)) de 0,95 estará delimitado:

\[\begin{align*} \hat{p} - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} \le & \pi \le \hat{p} + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1-\hat{p} \right)}{n}}\\ 0,34 - 1,96 \cdot \sqrt{ \frac{0,34 \cdot (1-0,34)}{400} } \le & \pi \le 0,34 + 1,96 \cdot \sqrt{ \frac{0,34 \cdot (1-0,34)}{n} }\\ 0,2936\le & \pi \le 0,3864 \end{align*}\]

Exemplo: Em uma amostra aleatória de 2000 eleitores do Brasil constatou-se uma intenção de voto de 43% para um candidato à presidência. Realizada a eleição, deseja-se inferir qual o intervalo de variação da proporção populacional a um nível de confiança de 99%.

Dados do problema:

• \(\hat{p}=0,43\) é a proporção amostral observada;
• o tamanho amostral (\(n=2000\)) é grande e a proporção amostral (\(\hat{p}=0,43\)) não é extrema (próxima a zero ou um);
  
• \(\pi\) é a proporção populacional (desconhecida); e,
• para o nível de confiança solicitado (\((1-\alpha)=0,99\)) temos da tabela \({z}_{\left(\frac{\alpha }{2}\right)}= +/-2,58\).

Um intervalo bilateral (fechado) para a proporção populacional desconhecida (\(\pi\)) sob um nível de confiança (\(1-\alpha\)) de 0,99 estará delimitado:

\[\begin{align*} \hat{p} - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} \le & \pi \le \hat{p} + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1-\hat{p} \right)}{n}}\\ 0,43 - 2,58 \cdot \sqrt{ \frac{0,43 \cdot (1-0,43)}{2000} } \le & \pi \le 0,43 + 2,58 \cdot \sqrt{ \frac{0,43 \cdot (1-0,43)}{2000} }\\ 0,4014\le & \pi \le 0,4586\\ \end{align*}\]

10.5.1 Intervalos de confiança para a diferença entre duas proporções amostrais

Para a construção de um intervalo de confiança para a diferença de duas proporções populacionais \(\pi_{X}\) e \(\pi_{Y}\) a partir das proporções obtidas em duas amostras de razoável tamanho (\(n_{X} \ge 30\) e \(n_{Y} \ge 30\)) e proporções amostrais \(\hat{p}_{X}\) e \(\hat{p}_{Y}\) não extremas (próximos a zero ou um) demosntra-se que a variável aleatória dessa diferença é tal que

\[ Z=\frac{(\hat{p}_{X}-\hat{p}_{Y} )- (\pi_{X}-\pi_{Y}) }{\sqrt{ \frac{\pi_{X}(1-\pi_{X})}{n_{X}}+ \frac{\pi_{Y}(1-\pi_{Y})}{n_{Y}}}} \sim N\left(0,1\right), \]

Sob as condições anunciadas, demostran-se que se pode tomar as proporções amostrais \(\hat{p}_{X}\) e \(\hat{p}_{Y}\) como aproximações diretas das proporções populacionais \(\pi_{X}\) e \(\pi_{Y}\) na expressão da variância da distribuição Normal que modela a distribuição das diferenças das proporções amostrais sem que isso resulte em grande alteração na distribuição da variável \(Z\).

\[ Z=\frac{(\hat{p}_{X}-\hat{p}_{Y} )- (\pi_{X}-\pi_{Y}) }{\sqrt{ \frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}} \sim N\left(0,1\right), \]

Assim podemos construir intervalos de confiança em torno da diferença das proporções populacionais \(\pi_{X}\) e \(\pi_{Y}\) associados a um nível de significância estabelecido:

Bilaterais: intervalo delimitado por dois valores: mínimo e máximo, para a proporção amostral, dentro do qual todos os valores possuem um mesmo nível de significância:

\[ P\left[(\hat{p}_{X}-\hat{p}_{Y}) - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{{\frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}} \\ \le \hspace{0.1cm} (\pi_{X}-\pi_{Y}) \hspace{0.1cm} \le \hspace{0.1cm} \\ (\hat{p}_{X}-\hat{p}_{Y}) + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{{\frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}}\right] = (1-\alpha) \]

Unilaterais: intervalos delimitados apenas em um de seus lados nos quais todos os valores possuem um mesmo nível de significância:

• Valor máximo (limitando à direita):

\[ P\left[(\pi_{X}-\pi_{Y}) \hspace{0.1cm} \le \hspace{0.1cm} (\hat{p}_{X}-\hat{p}_{Y}) + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{{\frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}}\right] = (1-\alpha) \]

• Valor mínimo (limitando à esquerda):

\[ P\left[(\pi_{X}-\pi_{Y}) \hspace{0.1cm} \ge \hspace{0.1cm} (\hat{p}_{X}-\hat{p}_{Y}) - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{{\frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}}\right] = (1-\alpha) \]