Capítulo 4 Introdução ao cálculo de probabilidades

Seria bom começar o capítulo sobre teoria das probabilidades, dando uma definição concisa, simples e intuitiva, todavia formalmente rigorosa. Infelizmente, isto não será possível.

Se por um lado, uma definição rigorosa de probabilidade requer um aparato matemático sofisticado e é bem pouco intuitiva; por outro lado as definições simples e frequentemente encontradas são tautológicas como:

Probabilidade é um número que quantifica, uma medida da informação disponível sobre a possibilidade de ocorrência de um determinado evento quando ainda não se sabe se ele ocorrerá ou não.

Essa definição é ``circular’’ ( definiendum = definien ) uma vez que se vale de um sinônimo de probabilidade (possibilidade) para se auto definir.

Todavia ela nos introduz dois conceitos que iremos usar como ponto de partida:

1. probabilidade refere-se a experimentos de resultado incerto (aleatórios);
2. que probabilidade é uma quantidade.

4.1 Introdução histórica

Os estudos de probabilidade surgiram no século XVII, motivados por questões práticas relacionadas a jogos de azar e decisões econômicas.

Uma das situações que estimulou essas discussões foi o problema apresentado pelo Cavaleiro de Méré (Chevalier de Méré), que envolvia jogos de azar com dados. Ele levantou duas questões principais sobre a probabilidade de certos resultados ao lançar dados, que acabaram influenciando o desenvolvimento da teoria probabilística.

A primeira questão envolvia o lançamento de um dado seis vezes, onde Méré acreditava que havia uma alta chance de obter pelo menos um “6”. Sua intuição estava correta: a probabilidade de não obter um “6” em seis lançamentos consecutivos é \((\frac{5}{6})^{6}\) , aproximadamente 33%, o que significa que a chance de obter pelo menos um “6” é de cerca de 67%.

O segundo problema que Méré trouxe era mais intrigante e envolvia o lançamento de dois dados 24 vezes. Ele acreditava que deveria obter pelo menos um duplo “6”, mas errou em sua previsão. A probabilidade de não obter um duplo “6” em 24 lançamentos consecutivos é \((\frac{35}{36})^{24}\), aproximadamente 51%, ou seja, a chance de obter um duplo “6” é apenas cerca de 49%, e não tão alta quanto ele esperava ao observar os resultados do jogo.

Essa discrepância entre intuição e realidade levou Méré a buscar ajuda com Pascal, e a subsequente troca de ideias com Fermat. Foi nessa correspondência entre Blaise Pascal e Pierre de Fermat em 1654, na qual discutiam problemas de divisão de apostas em jogos interrompidos, que se estabeleceu a base para o conceito de probabilidade esperada.

A formalização desses estudos avançou no século XVIII com a publicação da obra Ars Conjectandi (1713) de Jacob Bernoulli, que introduziu a lei dos grandes números. Essa lei estabelece que, com um número crescente de experimentos, a frequência observada de um evento tende a se aproximar de sua probabilidade verdadeira, fornecendo assim uma base teórica sólida para a análise de fenômenos aleatórios.

Outro avanço significativo veio com Abraham de Moivre, que em The Doctrine of Chances (1718) aplicou a teoria da probabilidade ao estudo de distribuições estatísticas, introduzindo a curva normal para modelar variáveis aleatórias. Ele também formalizou o conceito de esperança matemática, essencial para a análise de risco e a tomada de decisões em situações de incerteza.

No século XIX, Pierre-Simon Laplace sistematizou a teoria da probabilidade em sua obra Théorie Analytique des Probabilités (1812), onde ele introduziu a regra de Bayes, expandindo a aplicação da probabilidade para áreas como astronomia e ciências sociais. Sua abordagem permitiu que a probabilidade fosse utilizada para fazer inferências sobre eventos desconhecidos com base em informações prévias.

A evolução da teoria da probabilidade levou, no século XX, à sua formalização por meio da teoria da medida. Esta teoria, desenvolvida por matemáticos como Andrey Kolmogorov na década de 1930, deu à probabilidade um arcabouço rigoroso dentro da matemática, utilizando conceitos de medida para definir a probabilidade como uma função que mapeia eventos (subconjuntos de um espaço amostral) para valores numéricos entre 0 e 1. Esse formalismo ficou conhecido como modelo axiomático da probabilidade.

Esses axiomas são a base para o desenvolvimento de modelos probabilísticos consistentes e robustos, que hoje são amplamente utilizados em áreas como finanças, física, estatística e inteligência artificial.

Figure 4.1: Astralagus (um dos ossos que compõem o calcanhar, usado no Egito antigo como um dado rudimentar)

4.2 Conceitos essenciais

4.2.1 Experimentos determinísticos e experimentos aleatórios

Aleatório provem do latim: aleatorium: fato cujo desfecho depende de um acontecimento futuro e incerto, resultado da sorte ou acaso, acidental.

Probabilidade deriva do latim: probabilitas: qualidade do que se pode comprovar, de probabilis: o que pode passar por um teste, provável e de probare: provar, testar, examinar.

Ao contrário de um experimento determinístico, cujo resultado pode ser previamente determinado como :

• como a reação de dois átomos de hidrogênio com um átomo de oxigênio: \(2H_{2}+O_{2} \to 2H_{2}O\) e
• a distância \(S\) percorrida no vácuo sob velocidade constante \(V\) e sem atrito num intervalo de tempo \(t\): \(S = V \times t\)

o conceito de experimento aleatório é o que estabelece que seu resultado não pode ser previsto com certeza como em:

• o lançamento de um dado. O resultado pode ser qualquer número inteiro de 1 a 6 e
• a medição da altura de uma pessoa selecionada aleatoriamente.

Os resultados observados apresentam variações mesmo quando esses experimentos são repetidos indefinidamente e sob as mesmas condições; todavia, é possível estabelecer um conjunto cujos elementos compõem todos os possíveis resultados:

• qualquer número inteiro de 1 a 6: e o conjunto de possíveis resultados é finito e
• qualquer valor em um intervalo contínuo por exemplo, entre 1,50 m e 2,00 m (com infinitas possibilidades dentro desse intervalo).

4.2.2 O espaço amostral

A primeira coisa que fazemos quando começamos a pensar sobre a probabilidade de ocorrência de um certo resultado em um experimento aleatório é tentar listar todos os resultados com possibilidade de ocorrência.

Esses resultados formam um conjunto a que denominamos de espaço amostral que, usualmente, é representado pela letra grega maiúscula \(\Omega\).

Para que \(\Omega\) seja considerado o espaço amostral desse experimento aleatório ele precisa apresentar duas propriedades:

1. apenas um de seus elementos ocorre cada vez que realizamos o experimento aleatório; e,
2. pelo menos um dos possíveis resultados ocorre sempre que realizarmos o experimento aleatório.

Essas condições indicam que os elementos de \(\Omega\) são mutuamente exclusivos e exaustivos.

4.2.2.1 Espaços aleatórios discretos

• são finitos ou contáveis (infinito numerável)
• pode-se atribuir uma probabilidade para cada resultado

Exemplo 1:

• Experimento aleatório: lançar um dado e contar o número de pontos na face que ficar exposta para cima
• Espaço amostral finito: \(\Omega = \{1,2,3,4,5,6\}\)

Exemplo 2:

• Experimento aleatório: lançar dois dados e contar o número de pontos nas faces que ficarem expostas para cima
• Espaço amostral finito: \(\Omega = \{2,3,4,5,6,7,8,9,10,11,12\}\)

Exemplo 3:

• Experimento aleatório: lançar uma moeda e contar o número de lançamentos necessários até se obter uma “cara”
• Espaço amostral infinito contável: \(\Omega = \{1,2,3,4,5, \dots, k, \dots\}\)

Exemplo 4:

• Experimento aleatório: lançar um dado até se obter um “6”
• Espaço amostral infinito contável: \(\Omega = \{1,2,3,4,5, \dots, k, \dots\}\)

Um espaço amostral consiste então da enumeração (finita ou infinita contável) de todos os possíveis resultados de serem obtidos em um experimento aleatório.

Cada um dos possíveis resultados de um experimento aleatório é chamado de um elemento desse espaço amostral. Assim, para o espaço amostral \(\Omega\), seus elementos serão representados por letras gregas minúsculas \(\omega_{n}\)

\[ \Omega = \{\omega_{1}, \omega_{2}, \omega_{3}, ..., \omega_{n}, \dots \} \]

4.2.2.2 “Espaços” aleatórios contínuos

• não são contáveis: os resultados possíveis formam um intervalo contínuo de valores
• probabilidade de um resultado específico é zero: como existem infinitos resultados possíveis, a probabilidade de um valor específico é 0
• probabilidades são atribuídas a intervalos: a probabilidade de um evento é associada à extensão do intervalo (comprimento, área, volume, etc.) que o evento ocupa.

Exemplo 1:

• Experimento aleatório: a altura de uma pessoa aleatoriamente sorteada
• Intervalo amostral: \(\Omega = [1,5 ; 2,0 ]\) m

Exemplo 2:

• Experimento aleatório: o peso de uma pessoa aleatoriamente sorteada
• Intervalo amostral: \(\Omega = [10 ; 100 ]\) kg

Exemplo 3:

• Experimento aleatório: o teor de um minério por quuilo de uma amostra de solo extraída de um local aleatório
• Intervalo amostral: \(\Omega = [0,001 ; 0,01]\) gramas

4.2.2.3 Espaços amostrais equiprováveis e não equiprováveis

Se todos os elementos que compõem um espaço amostral finito de um experimento aleatório possuem a mesma probabilidade de ocorrência é dito que o espaço amostral desse experimento aleatório é equiprovável (com a mesma probabilidade para todos os seus elementos).

Exemplo 1

• Experimento aleatório: lançar um dado e contar o número de pontos na face que ficar exposta para cima
• Espaço amostral finito: \(\Omega = \{1,2,3,4,5,6\}\)
• Probabilidades: \(P(1)=\frac{1}{6},P(2)=\frac{1}{6},\\P(3)=\frac{1}{6},P(4)=\frac{1}{6},\\P(5)=\frac{1}{6},P(6)=\frac{1}{6}\)

> Exemplo 2

• Experimento aleatório: lançar dois dados e contar o número de pontos nas faces que ficarem expostas para cima
• Espaço amostral finito: \(\Omega = \{2,3,4,5,6,7,8,9,10,11,12\}\)
• Probabilidades: \(P(2)=\frac{1}{36},P(3)=\frac{2}{36},P(4)=\frac{3}{36},P(5)=\frac{4}{36},\\P(6)=\frac{5}{36},P(7)=\frac{6}{36}, P(8)=\frac{5}{36}, P(9)=\frac{4}{36},\\ P(10)=\frac{3}{36}, P(11)=\frac{2}{36}, P(12)=\frac{1}{36}\)

Cada um dos elementos que compõem o espaço amostral (a soma dos valores numéricos das faces no lançamento de um dado por duas vezes) poderá resultar de diferentes combinações de valores.

A Tabela 4.1 apresenta todas as combinações possíveis de serem obtidas, bem como as proporções em relação ao total para cada elemento do espaço amostral.

Table 4.1: Quadro dos possíveis resultados de um experimento aleatório: somas dos valores numéricos das faces no lançamento de um dado por duas vezes

Soma	Possíveis combinações de resultados nos lançamentos	Frequência \(n_{i}\)	Proporção \(f_{i}\)
	(primeiro,segundo)
2	(1,1)	1	\(\frac{1}{36}\)
3	(1,2); (2,1)	2	\(\frac{2}{36}\)
4	(1,3); (2,2); (3,1)	3	\(\frac{3}{36}\)
5	(1,4); (2,3); (3,2); (4,1)	4	\(\frac{4}{36}\)
6	(1,5); (2,4); (3,3); (4,2); (5,1)	5	\(\frac{5}{36}\)
7	(1,6); (2,5); (3,4); (4,3); (5,2); (6,1)	6	\(\frac{6}{36}\)
8	(2,6); (3,5); (4,4); (5,3); (6,2)	5	\(\frac{5}{36}\)
9	(3,6); (4,5); (5,4); (6,3)	4	\(\frac{4}{36}\)
10	(4,6); (5,5); (6,4)	3	\(\frac{3}{36}\)
11	(5,6); (6, 5)	2	\(\frac{2}{36}\)
12	(6,6)	1	\(\frac{1}{36}\)
Totais		36	\(1\)

As probabilidades de ocorrência de cada um os elementos desse espaço amostral são diferentes e, por essa razão é dito que o espaço amostral desse experimento aleatório tem elementos não equiprováveis.

4.2.3 Evento

Define-se como evento de interesse um subconjunto finito do espaço amostral, composto por um ou mais de seus elementos que satisfazem o enunciado estabelecido no experimento aleatório proposto.

A expressão evento de interesse (também chamado de sucesso) refere-se, no contexto do cálculo de probabilidades, à ocorrência de um resultado desejado durante a realização de um experimento aleatório.

Frequentemente, eventos de interesse são representados por letras maiúsculas do alfabeto romano e podem ser acompanhados de uma notação explicativa, como \(E(\dots)\).

Por exemplo, considere um experimento aleatório que consiste em lançar um dado uma única vez. Um possível evento de interesse pode ser: E(obtenção do número 2) (\(E(2)\)) e, nesse contexto pode ser a obtenção do número 2 como resultado.

Podemos ter variados tipos de eventos de interesse como:

1. simples ou compostos;
2. certos ou impossíveis;
3. dependentes ou independentes ;
4. mutuamente exclusivos ;
5. complementares;

4.2.3.1 Diagramas de Venn para representar o espaço amostral e eventos de interesse

Em muitos dos problemas de probabilidade, o evento de interesse pode se definido como associações de dois ou mais eventos formados, por sua vez, por um ou mais elementos do espaço amostral do experimento aleatório. Uniões, interseções e complementos são algumas dessas associações que, doravante, serão muito utilizados.

Por essa razão, a representação do espaço amostral e esses eventos por meio de Diagramas de Venn pode ajudar a compreensão de um problema de cálculo probabilidade.

Figure 4.2: John Venn, 1834–1923

4.2.3.1.1 União \(A \cup B\)

Sejam \(A\) e \(B\) dois eventos de interesse definidos sobre o espaço amostral \(\Omega=\{1,2,3,4,5,6\}\) (lançamento de um dado) tais que \(A=\{1,2,3\}\) e \(B=\{2,4,6\}\).

Um evento de interesse \(E\) expresso como a união desses dois outros, representado por \(E=(A \cup B)\), será o subconjunto do espaço amostral \(\Omega\) que contém os elementos que pertençam a \(A\), ou a \(B\) ou a ambos.

Desse modo, \(E=A \cup B=\{1,2,3,4,6\}\) e o Diagrama de Venn correspondente será:

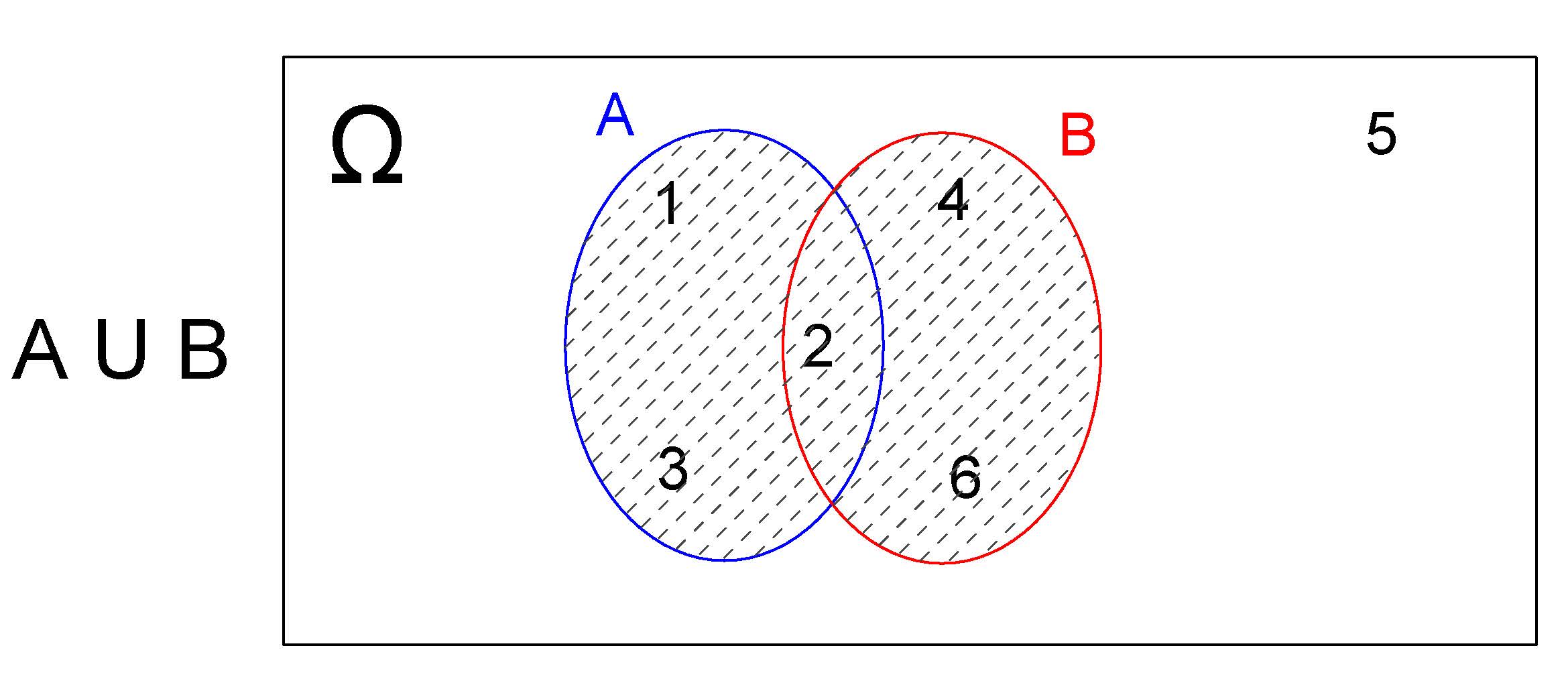
Figure 4.3: União: \(A \cup B\)

Na realização desse experimento aleatório (lançar um dado) o evento de ineteresse \(E\) ocorrerá quando qualquer um dos resultados for um elemento pertencente a \(A\), ou a \(B\) ou a ambos.

4.2.3.1.2 Interseção \(A \cap B\)

Um evento de interresse \(E\) definido como a interseção dos eventos \(A\) e \(B\) anteriormente definodos, representado por \(E=(A \cap B)\), será o subconjunto do espaço amostral \(\Omega\) que contém todos os elementos que pertençam a ambos os eventos A e B simultaneamente.

Desse modo, \(E=(A \cap B) =\{2\}\) e o Diagrama de Venn correspondente será:

Figure 4.4: Interseção: \(A \cap B\)

Na realização desse experimento aleatório (lançar um dado) o evento de interesse \(E\) ocorrerá apenas quando o resultado for um elemento simultaneamente pertencente a \(A\) e \(B\) .

Quando o evento de interesse é definido pela interseção de dois outros, todavia esssa interseção é vazia, representa-se \(E\) como

\[ E(A \cap B) = \varnothing \]

4.2.3.1.3 Complemmento \(A^{c}\)

Um evento de intersse pode também ser definido como o complemento de outros como, por exemplo, de \(A\), sendo representado representado por \(E=(A^{c})\) (ou \(E=(\stackrel{-}{A})\)).

Desse modo, \(E=(A^{c}) =\{4,5,6\}\) e o Diagrama de Venn correspondente será:

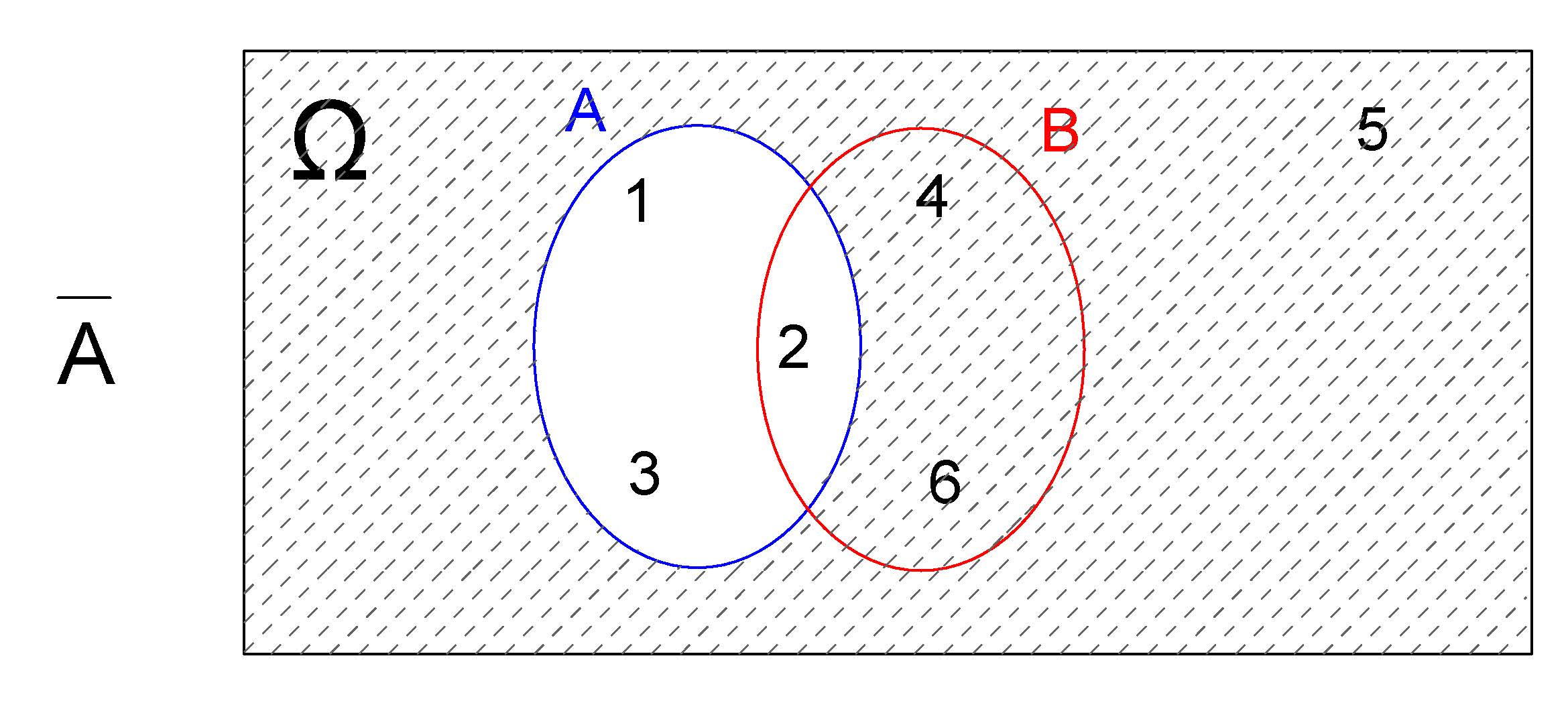
Figure 4.5: Complementar \(A^{c}\)

De modo análogo, para \(E=(B^{c})=\{1,3,5\}\) e o Diagrama de Venn correspondente será :

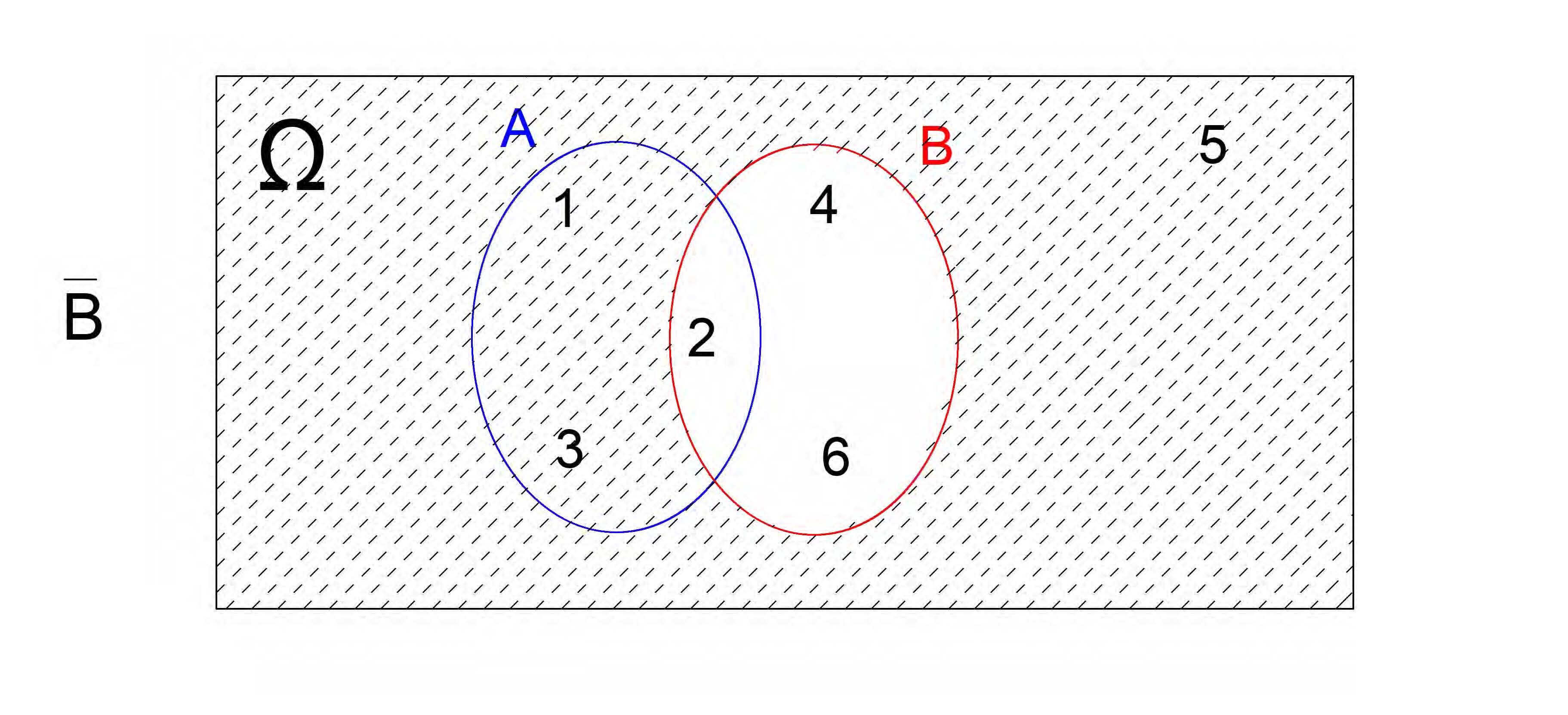
Figure 4.6: Complementar de B

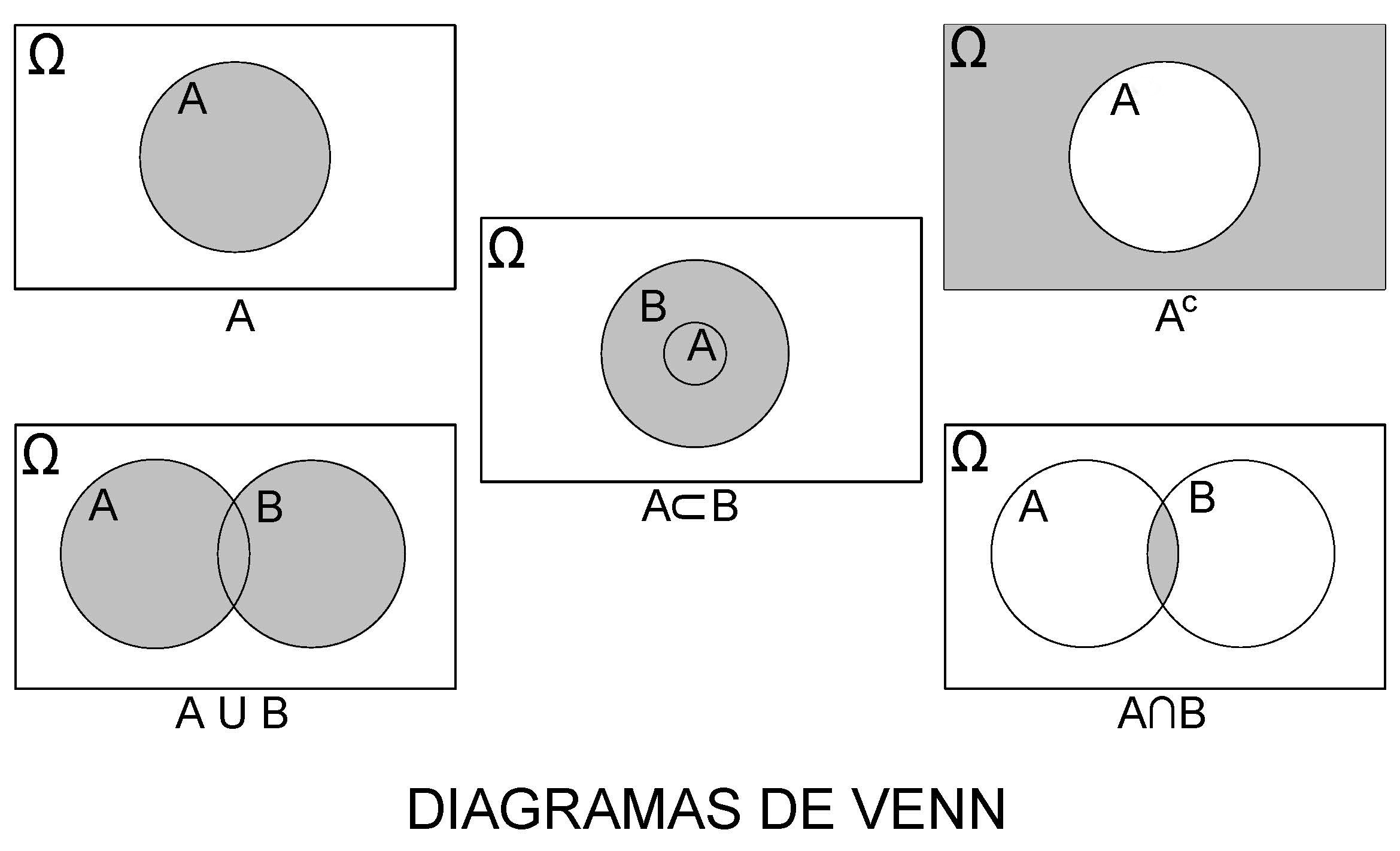
Figure 4.7: Diagramas de Venn

4.2.3.2 Eventos simples e eventos compostos

O evento de interesse (\(E(2)\)) definido no experimento aleatório anterior (obter o número 2) é formado por apenas um elemento do espaço amostral. Eventos formados por apenas um elemento do espaço amostral são denominados de evento simples.

\[ \Omega = \{1; 2; 3; 4; 5; 6\}\\ E(2) = \{2\} \]

Admita agora o mesmo experimento aleatório todavia definindo como evento de interesse (Eobter-se um número par. Um evento de interesse assim definido é um evento composto uma vez que é formado por mais de um elemento do espaço amostral:

\[ \Omega = \{1; 2; 3; 4; 5; 6\}\\ E(par) = \{2; 4; 6\} \]

Outro exemplo, a partir de um experimento aleatótrio que consiste em se lançar uma moeda duas vezes, cujo espaço amostral é representado por um conjunto composto por quatro elementos

\[ \Omega = \{(\text{Cara}, \text{Coroa}),(\text{Coroa}, \text{Cara}),(\text{Cara}, \text{Cara}), (\text{Coroa}, \text{Coroa})\} \]

Se definirmos como evento de interesse na realização desse experimento aleatório obter-se \(E=\{(Cara, Cara)\}\), o evento \(E\) será um evento simples pois é formado por apenas um elemento do espaço amostral.

Se, por outro lado, definimos como sucesso obter-se \(E_{1}=\{(Cara, Coroa) \text{ ou } (Coroa, Cara)\}\), o evento \(E_{1}\) será um evento composto pois é formado por dois elementos do espaço amostral.

Se codificarmos Cara=1 e Coroa=0, podemos representar num plano \(XY\) o espaço amostral \(\Omega\) desse experimento aleatório e o evento de sucesso \(E_{1}\)

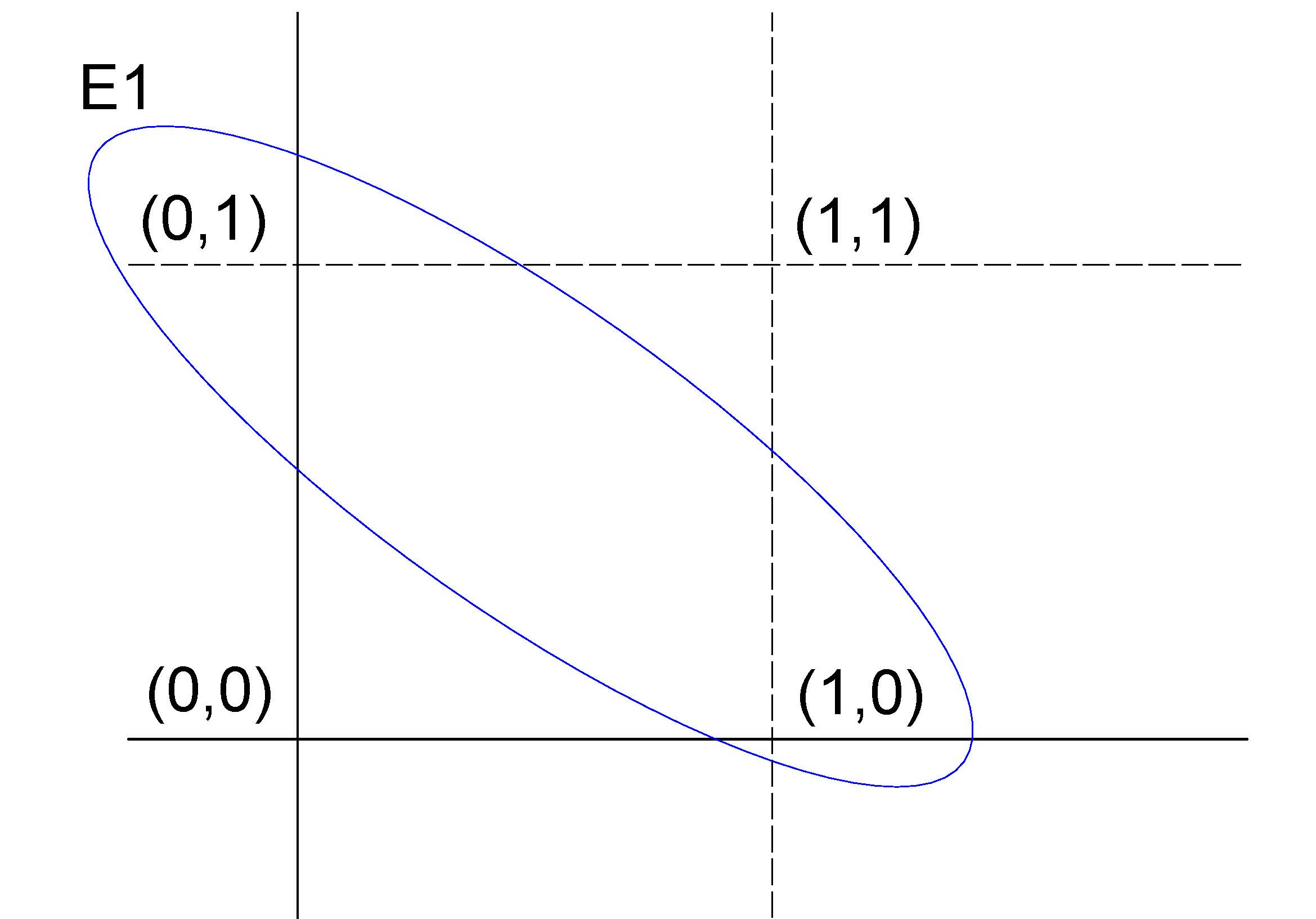
Figure 4.8: Representação gráfico do espaço amostral do experimento aleatório e do evento de interesse definido

4.2.3.3 Eventos certos e eventos impossíveis

Um evento de interesse \(G\), definido sobre o espaço amostral \(\Omega\), em que \(G = \Omega\), expressa que qualquer elemento de \(\Omega\) satisfaz o evento \(G\), ou seja, qualquer um dos possíveis resultados do experimento aleatório corresponde ao evento.

Um evento de interesse assim definido ocorrerá com certeza, razão pela qual tais eventos são denominados eventos certos.

Por outro lado, se definirmos um evento de interesse \(I\) que não contém resultados pertencentes a \(\Omega\) — o espaço amostral, ou seja, todos os resultados possíveis — como, por exemplo, obter o número 7 no lançamento de um dado de seis faces, esse evento será impossível de ocorrer.

Eventos assim definidos são chamados de eventos impossíveis.

4.2.3.4 Eventos independentes

Dois eventos são considerados independentes quando a probabilidade de ocorrência de um evento de interesse em um determinado experimento aleatório não é influenciada pelo resultado prévio de outro evento.

Em outras palavras, a ocorrência de um evento não altera a probabilidade do outro. Caso contrário, esses eventos são classificados como dependentes ou condicionados.

Este conceito será explorado em maior detalhe em seções posteriores.

4.2.3.5 Eventos mutuamente exclusivos

Dois eventos que nunca poderão ocorrer simultaneamente são ditos mutuamente exclusivos. No experimento do lançamento da moeda por uma vez, nunca observaremos, simultaneamente, dois eventos como \(E=\{(Cara)\}\) e \(F=\{(Coroa)\}\).

Um evento assim definido teria sua interseção vazia

\[ G=(E \cap F) = \varnothing \]

e, por essa razão, sua probabilidade será \(P(G)=P(E \cap F)=0\).

4.2.3.6 Eventos complementares

Definido um evento de interesse qualquer pode-se observar apenas dois resultados:

1. ocorrer;
2. não ocorrer o sucesso.

Ou seja, um ou outro deverá forçosamente ocorrer.

Chama-se de evento complementar (\(E^{c}\) ou \(\stackrel{-}{E}\)) a um evento (\(E\)) e sua probabilidade de sucesso será:

\[ P(E^{c}) = 1 - P(E) \]

Se a probabilidade de sucesso de que ele ocorra for \(P(E)=p\) e a de que ele não ocorra for \(P(E^{c}= q)\) vê-se que a soma dessas quantidades deverá ser \(p + q =1\), novamente antecipando um dos postulados do conceito axiomático de probabilidade.

4.2.4 Probabilidade

4.2.4.1 Conceito clássico ou a priori

Sob uma visão intuitiva, a probabilidade como uma medida da informação que temos sobre a possibilidade de ocorrência de um evento aleatório, pode ser definida como a medida numérica expressa em termos relativos (percentuais), obtida pela razão (proporção) entre o número de eventos favoráveis (sucessos) pelo número total de eventos prováveis no experimento (espaço amostral).

Esse conceito de probabilidade é denominado clássico ou a priori, baseado em um conhecimento prévio ou uma crença subjetiva sobre a probabilidade de um evento ocorrer.

Por exemplo, um jogador de cartas pode ter uma crença a priori de que a probabilidade de uma carta ser um ás é de 1 em 13, independentemente do número de baralhos no jogo

A distribuição de frequências é um instrumento importante para a análise da variabilidade de experimentos aleatórios e, em particular, as frequências relativas são estimativas das probabilidades.

\[ P(E)= \frac{\text{número de resultados de interesse (sucessos)}}{\text{número total de resultados possíveis no espaço amostral}} \]

Com o estabelecimento de suposições adequadas, um modelo teórico de probabilidade pode ser empregado sem a realização a priori do experimento aleatório, reproduzindo de modo razoável a distribuição das frequências quando o experimento é realizado.

Consideremos o exemplo do experimento que consiste em se lançar um dado e observar o valor numérico de sua face. As suposições que deveriam ser estabelecidas a priori são:

• só pode ocorrer uma das seis faces; e,
• o dado utilizado não possui viés algum (não favorece face alguma).

Como todos os \(N\) resultados do espaço amostral apresentam uma mesma probabilidade de ocorrência, então a proporção teórica de ocorrência de qualquer um desse resultados poderá ser apresentado na forma vista na na forma vista na Tabela 4.2.

\[ P(E)= \frac{1}{N} \]

Table 4.2: Distribuição das proporções teóricas do um experimento aleatório: lançamento de um dado

Face	1	2	3	4	5	6	Total
Proporção teórica	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	\(\frac{1}{6}\)	1

Sendo equiprováveis todos os elementos do espaço amostral, todos terão a mesma probabilidade de ocorrência que será:

\[\begin{align*} P(E) = & \frac{1}{N} \\ = & \frac{1}{6} \\ = & \frac{1}{6} \end{align*}\]

Por essa razão sabe-se, a priori a probabilidade de ocorrência de qualquer evento ao se realizar esse tipo de experimento aleatório uma única vez.

4.2.4.2 Conceito frequentista ou a posteriori

Todavia, se realizarmos o experimento aleatório anterior apenas algumas, tal regularidade poderá não ser comprovada: as frequências observadas (as quantidades obtidas para cada um dos valores numéricos das faces) apresentarão uma grande irregularidade diferindo das frequência teóricas definidas.

Observa-se que os resultados das frequências observadas irá se estabilizar, aproximando-se das frequências teóricas, à medida que se repete esse experimento um número suficientemente grande de vezes.

A definição frequencial (a posteriori):

1- refere-se à probabilidade empírica observada a posteriori; 2- tem por objetivo estabelecer um modelo adequado à interpretação de alguns tipos de experimentos aleatórios; e, 3- é a base para se formular um modelo teórico de distribuição de probabilidades como os que serão abordados mais adiante.

Ao se repetir o experimento aleatório um grande número de vezes ( \(n\) tendendo a infinitas vezes), a quantidade de vezes que um determinado resultado foi verificado dividida por o número de repetições realizadas (\(n\)) irá se aproximar de sua proporção teórica. É o que se denomina como regularidade estatística dos resultados por essa propriedade não mais se necessita que os eventos sejam equiprováveis.

Formalmente conhecida como Lei Fraca dos Grandes Números (um dos pilares da teoria da probabilidade, foi formalizada pelo matemático suíço Jakob Bernoulli em 1713) e estabelece uma convergência para a probabilidade: à medida que o número de ensaios independentes de um experimento aleatório aumenta, a frequência relativa dos sucessos observados tende a se aproximar da probabilidade teórica

\[ P\left(E\right)=\underset{n\to \infty }{lim}{\frac{F(E)}{n}} \]

onde:

• \(P(E)\) é a probabilidade de ocorrência do evento \(E\);
• \(F(E)\) é a frequência observada do evento \(E\) (o número de vezes que ele ocorre em n repetições); e,
• \(n\) é o número de repetições do experimento.

Jakob Bernoulli in 1713

4.2.4.2.1 Simulações

As simulações desempenham um papel fundamental no entendimento prático dos conceitos probabilísticos, permitindo a reprodução de experimentos aleatórios em larga escala.

Por meio de simulações, podemos verificar empiricamente a convergência das frequências observadas para as frequências teóricas discutidas nos conceitos anteriores.

Elas fornecem uma ferramenta poderosa para ilustrar a regularidade estatística dos resultados, especialmente em situações em que realizar o experimento real seria impraticável ou custoso.

Ao simular o lançamento de um dado, por exemplo, é possível observar como a frequência relativa de qualquer face começa a se aproximar da probabilidade teórica (\(P(\cdot)=\frac{1}{6}\)) à medida que aumentamos o número de repetições.

# Função para lançar o dado n vezes e calcular a frequência de uma face específica

lancar_dado <- function(n, face_escolhida) {
  # Definindo as faces do dado
  faces <- 1:6

  # Realizando n lançamentos
  lancamentos <- sample(faces, n, replace = TRUE)

  # Calculando a frequência observada da face escolhida
  frequencia <- sum(lancamentos == face_escolhida) / n * 100

  # Exibindo a frequência em percentual
  cat("A frequência observada da face", face_escolhida, "foi de", frequencia, "%\n")
}

lancar_dado(10, 3)

## A frequência observada da face 3 foi de 10 %

lancar_dado(10000, 3)

## A frequência observada da face 3 foi de 16.35 %

Ao simular o lançamento de um dado, por exemplo, é possível observar como as frequências relativas de todas as faces começam a se aproximar das probabilidades teóricas (\(P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=\frac{1}{6}\)) à medida que aumentamos o número de repetições.

library(ggplot2)

lanca_dado <- function(numero_de_lancamentos) {
  # Gere os lançamentos do dado
  lancamentos <- sample(1:6, numero_de_lancamentos, replace = TRUE)

  # Crie um data frame com os resultados
  dados <- data.frame(Face = lancamentos)

  # Contagem das ocorrências de cada face
  contagem <- table(dados$Face)

  # Crie um gráfico de barras com o número de lançamentos no título
  grafico <- ggplot(data = data.frame(Face = names(contagem), Contagem = as.numeric(contagem)),
                    aes(x = Face, y = Contagem)) +
    geom_bar(stat = "identity") +
    labs(x = "Face do Dado", y = "Contagem") +
    ggtitle(paste("Lançamento de um Dado por:", numero_de_lancamentos, "vezes")) +
    theme_minimal()

  # Exiba o gráfico
  print(grafico)
}

lanca_dado(10)

Figure 4.9: Histograma das frequências observadas em 10 lançamentos de um dado justo, evidenciando a variabilidade significativa nas frequências relativas, mesmo que todos os resultados sejam igualmente prováveis.

lanca_dado(10000)

Figure 4.10: Histograma das frequências observadas em 10.000 lançamentos de um dado justo, ilustrando a convergência assintótica das frequências relativas de cada resultado para sua probabilidade teórica, considerando que todos os resultados são igualmente prováveis.

Ao simular o lançamento de dois dados, por exemplo, é possível observar como as frequências relativas de todas as possíveis somas das faces começam a se aproximar das probabilidades teóricas:

\[ P(2) = P(12) = \frac{1}{36}, \\ P(3) = P(11) = \frac{2}{36}, \\ P(4) = P(10) = \frac{3}{36}, \\ P(5) = P(9) = \frac{4}{36}, \\ P(6) = P(8) = \frac{5}{36}, \\ P(7) = \frac{6}{36} \]

à medida que aumentamos o número de repetições.

library(ggplot2)

lanca_dois_dados <- function(numero_de_lancamentos) {
  # Gere os lançamentos dos dois dados
  dado1 <- sample(1:6, numero_de_lancamentos, replace = TRUE)
  dado2 <- sample(1:6, numero_de_lancamentos, replace = TRUE)

  # Calcule a soma dos dois dados
  somas <- dado1 + dado2

  # Crie um data frame com os resultados
  dados <- data.frame(Soma = somas)

  # Contagem das ocorrências de cada soma
  contagem <- table(dados$Soma)

  # Crie um data frame com a proporção de cada soma
  dados_grafico <- data.frame(
    Soma = as.numeric(names(contagem)),
    Contagem = as.numeric(contagem),
    Proporcao = as.numeric(contagem) / numero_de_lancamentos
  )

  # Probabilidades teóricas de cada soma
  prob_teoricas <- c(1/36, 2/36, 3/36, 4/36, 5/36, 6/36, 5/36, 4/36, 3/36, 2/36, 1/36)
  somas_teoricas <- 2:12
  prob_teoricas_formatadas <- paste0("(", round(prob_teoricas * 100, 2), "%)")

  # Adicione as probabilidades teóricas ao eixo x como rótulos
  labels_eixo_x <- paste(somas_teoricas, prob_teoricas_formatadas)

  # Crie o gráfico de barras com as frequências observadas e as probabilidades teóricas no eixo x
  grafico_somas <- ggplot(data = dados_grafico, aes(x = Soma, y = Proporcao)) +
    geom_bar(stat = "identity", fill = "steelblue") +
    geom_text(aes(label = scales::percent(Proporcao, accuracy = 0.1)), vjust = -0.5) +  # Exibe as proporções acima das barras
    scale_x_continuous(breaks = somas_teoricas, labels = labels_eixo_x) +  # Define os rótulos com soma e probabilidade
    scale_y_continuous(labels = scales::percent) + # Formata o eixo y como porcentagem
    labs(x = "Soma dos Dados (Probabilidade Teórica)", y = "Proporção das Observações (%)") +
    ggtitle(paste("Lançamento de Dois Dados por:", numero_de_lancamentos, "vezes")) +
    theme_minimal()

  # Exiba o gráfico
  print(grafico_somas)
}

lanca_dois_dados(10)

Figure 4.11: Histograma das frequências observadas em 10 lançamentos de dois dados justos, evidenciando a diferença significativa das frequências relativas observadas em relação às probabilidades teóricas de cada resultado possível.

lanca_dois_dados(10000)

Figure 4.12: Histograma das frequências observadas em 10.000 lançamentos de dois dados justos ilustrando a convergência assintótica das frequências relativas observadas para as probabilidades teóricas de cada resultado possível.

4.2.4.3 Conceito axiomático

Esta abordagem é baseada em um conjunto de axiomas matemáticos que definem as propriedades básicas de probabilidades. A probabilidade é definida como uma função de conjuntos que atribui a cada conjunto de eventos um número entre 0 e 1, satisfazendo os axiomas matemáticos de probabilidade. Essa abordagem permite que as probabilidades sejam definidas formalmente e usadas para cálculos matemáticos.

Um axioma é uma premissa considerada necessariamente evidente e verdadeira, fundamento de uma demonstração, porém ela mesma indemonstrável, originada, segundo a tradição racionalista, de princípios inatos da consciência ou, segundo os empiristas, de generalizações da observação empírica.

Admita \(P\) uma função que opera sobre o espaço \(\Omega\); isto é, uma função que associa uma quantidade \(P(\Omega)\) a cada elemento \(\omega\) \(\in\) \(\Omega\).

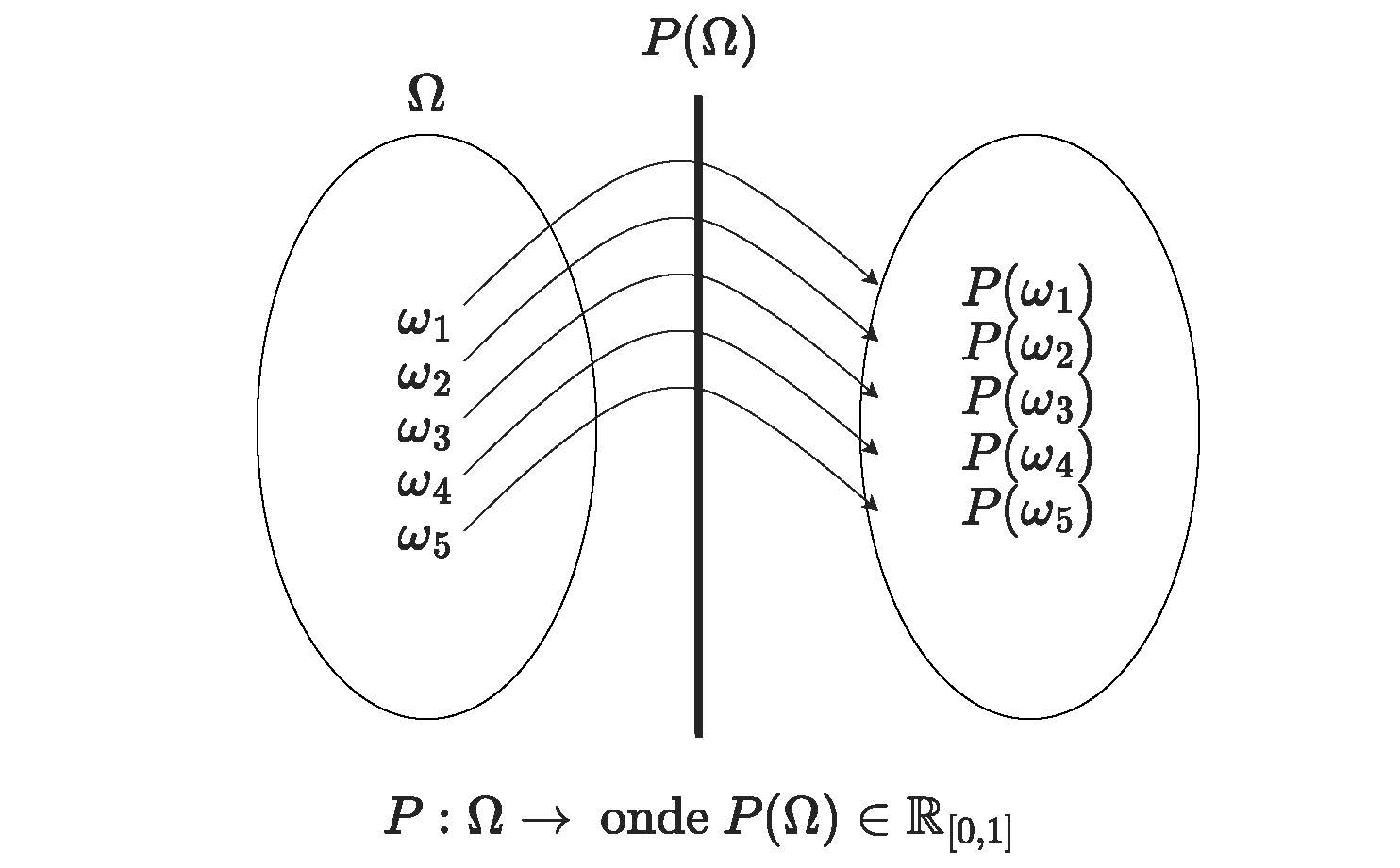
Figure 4.13: Representação gráfica da função \(P(\Omega)\)

Essa função \(P\) será uma função de probabilidade se, e somente se, satisfizer a três axiomas (postulados: conceitos iniciais necessários à construção ou aceitação de uma teoria) estabelecidos por Andrey Kolmogorov (1933).

Figure 4.14: Andrey Nikolaevich Kolmogorov (1903-1987)

Kolmogoroff afirmou que uma Teoria das probabilidades poderia ser desenvolvida a partir de axiomas, da mesma forma que a geometria e a álgebra, e a considerou como caso especial da Teoria da medida e integração desenvolvida por Lebesgue, Borel e Fréchet. Ele estabeleceu como postulados as propriedades comuns das noções de probabilidade clássica e frequentista que, desta forma, viraram casos particulares da definição axiomática.

4.2.4.3.1 Postulado do intervalo

A probabilidade de qualquer \(E\) é um número real entre 0 e 1 (pode-se entender isso como uma convenção, onde então se estabelece a medida da probabilidade é um número positivo e que qualquer evento pode ter probabilidade de, no máximo, 1). Esse postulado está plenamente de acordo com a interpretação frequentista de probabilidade.

\[ P(E) \ge 0 \text{ (não negatividade e,)}\\ \text{mais especificamente, }\\ 0 \hspace{0.5cm} \le P(E) \hspace{0.5cm} \le 1 \]

4.2.4.3.2 Postulado da certeza (normalização)

O segundo postulado refere-se à probabilidade do evento certo ser igua a 1. No que diz respeito à interpretação frequentista, uma probabilidade de 1 implica que o evento em questão ocorrerá 100% do tempo ou, em outras palavras, que é certo que ele ocorra (como, p. exemplo, um experimento aleatório de se lançar dois dados e somar o valor de suas faces o evento certo poderia ser definido como observar uym valor menor que 13 ou maior que 2)

\[ P(\Omega) = 1 \]

4.2.4.3.3 Postulado da aditividade para eventos mutuamente exclusivos (aditividade)

\[ P\left(\bigcup _{n=1}^{\infty }{\omega}_{n}\right)=\sum _{n=1}^{\infty }P\left({\omega}_{n}\right) \]

para qualquer sequência de eventos mutuamente exclusivos \(\{\omega_{1}, \omega_{2}, \omega_{3}, ..., \omega_{n}, ...\}\) (isto é, tal que \(\omega_{i} \cap \omega_{j} \varnothing\) se \(i \neq j\))

Tomando o terceiro postulado no caso mais simples, isto é, para dois eventos mutuamente exclusivos \(\omega_{1}\) e \(\omega_{2}\), pode ser facilmente visto que é satisfeito pela interpretação frequentista.

Se um evento ocorrer, digamos, 28% das vezes, outro evento ocorrerá 39%, e os dois eventos não podem ocorrer ao mesmo tempo (ou seja, são mutuamente exclusivos), então um ou outro evento} ocorrerão em 28 + 39 = 67% das vezes. Assim, o terceiro postulado é satisfeito, e o mesmo tipo de argumento se aplica quando há mais de dois eventos mutuamente exclusivos.

Recapitulando

1- foi definido o conceito de experimento aleatório como sendo aquele cujos resultados não podem ser determinados com certeza antes de sua realização;
2- foi definido o conceito de espaço amostral de um experimento aleatório como sendo o conjunto de todos os possíveis resultados que ele pode apresentar;
3- foi definido que um evento de interesse é um subconjunto do espaço amostral no qual estamos particularmente interessados;
4- foi definida uma função que tem como domínio o espaço amostral e associa uma quantidade (entre 0 e 1) a cada elemento do espaço amostral; e, por fim,
5- estabelecemos que se essa função atende a três postulados então ela será uma medida da probabilidade de ocorrẽncia de cada evento do espaço amostral em questão.

Assim, quando uma função \(P\) associa uma quantidade \(P(\Omega)\) a um evento \(\omega\) e \(P(\Omega)\) atende aos três axiomas anteriormente estabelecidos, diz-se que que ela é a função de probabilidade de \(\Omega\).

4.3 Probabilidade da união de eventos

Considerem o espaço amostral de um experimento que consiste no lançamento de um dado honesto: \(S=\{1,2,3,4,5,6\}\) e admitam alguns eventos constituídos sobre esse espaço mostral, abaixo descritos:

\[ E_{1}=\{par\},\\ E_{2}=\{ímpar\},\\ E_{3}=\{1,2,3\},\\ E_{4}=\{4,5,6\},\\ E_{5}=\{\ge4\},\\ E_{6}=\{\le5\}.\\ \]

A partir desses eventos podemos propros novos eventos de interesse a partir de uniões (conectivo \(\cup\)) de dois (ou mais) dos eventos originais como, por exemplo,

\[ H_{a}=E_{1} \cup E_{2},\\ H_{b}=E_{1} \cup E_{4},\\ H_{c}=E_{2} \cup E_{3},\\ H_{d}=E_{2} \cup E_{5},\\ H_{e}=E_{4} \cup E_{6},\\ H_{f}=E_{3} \cup E_{5}. \].

No experimento aleatório estabelecido:

• lembrando que a união de dois conjuntos é o conjunto formado pelos elementos que estão em um, no outro ou em ambos, e
  
• pensando em probabilidade como a razão do “número de resultados favoráveis” pelo “número de resultados possíveis” (conceito a priori)

podemos fcimente verificar que as probabilidades de ocorrência desses eventos são:

\[ P(H_{a})=1\\ P(H_{b})=P(H_{c})=P(H_{d})=P(H_{e})=\frac{1}{3}\\ P(H_{f})=0\\ \]

Considerem agora a Tabela 4.3, de dupla entrada, na qual vemos a distribuição dos alunos de uma escola conforme seu sexo e o curso:

Table 4.3: Distribuição da quantidade de alunos segundo seu sexo e curso escolhido

Curso	Sexo
	Masculino (M)	Feminino (F)	Total
Matemática pura (M)	70	40	110
Matemática aplicada (A)	15	15	30
Estatística (E)	10	20	30
Computação (C)	20	10	30
Total	115	85	200

Essa tabela nos possibilita calcular a probabilidade de ocorrência de diversos eventos de interesse que desejemos estabelecer.

Exemplo: seja o experimento aleatório de se escolher, aleatoriamente, um estudante qualquer desses quatro cursos. Assim, se definimos nosso evento de interesse \(M\) como sendo M:sexo masculino, a probabilidade de sucesso (que o indivíduo sorteado aleatoriamente seja do sexo masculino) será:

\[ P(M) = \frac{115}{200} \]

Exemplo: se nosso evento de interesse \(A\) como sendo \(A:\) curso de matemática aplicada , a probabilidade de sucesso (que o indivíduo sorteado aleatoriamente seja do curso de matemática aplicada será):

\[ P(A) = \frac{30}{200} \]

A partir dos eventos de interesse anteriormente estabelecidos, podemos definir outros eventos na forma de uniões (\(\cup\)) e interseções (\(\cap\)):

• uma união entre os dois eventos de interesse anteriores \(A\) e \(M\) é representada por \(A \cup M\) (alternativamente lê-se também ou) e representa um evento onde pelo menos um dos dois eventos básicos pode ocorrer: ou \(A\), ou \(M\) ou ambos; e,
  
• uma interseção dos dois eventos de interesse anteriores \(A\) e \(M\) é representada por \(A \cap M\) (alternativamente lê-se também e) e representa um evento onde os dois eventos básicos devem ocorrer: \(A\) e \(M\).

Exemplo: se definimos nosso evento de interesse (\(P(A \cap M)\)) como sendo sexo masculino e cursando matemática aplicada. Facilmente podemos visualizar na Tabela 4.3 que apenas 15 alunos do curso do evento de interesse (matemática aplicada) são do sexo do segundo evento de interesse (masculino), em relação a todo espaço amostral e assim:

\[ P(A \cap M) = \frac{15}{200} \].

Exemplo: consideremos agora o evento de interesse (\(P(A \cup M)\)) como sendo sexo masculino ou cursando matemática aplicada.

Na Tabela 4.3 temos as duas probabilidades marginais:

1. \(P(A)=\frac{30}{200}\) (curso: matemática aplicada); e, 2- \(P(M)=\frac{115}{200}\) (sexo masc).

Poderíamos intuir equivocadamente que:

\[ P(A \cup M) = P(A) + P(M) = \frac{30}{200} + \frac{115}{200} = \frac{145}{200} \]

Tal raciocínio é errado pois iria considerar por duas vezes os alunos do sexo masculino. Uma fração da quantidade global (115) de alunos do sexo masculino já considera aqueles que estão matriculados no curso de matemática aplicada (15). É preciso subtrair da soma das probabilidades marginais essa parcela em comum que é a interseção dos dois eventos básicos.

A resposta correta será:

\[ P(A \cup M) = P(A) + P(M) - P(A \cap M) = \frac{30}{200} + \frac{115}{200} -\frac{15}{200} = \frac{130}{200} \].

Portanto, para quaisquer eventos de intersse \(A\) e \(B\), podemos estabelecer uma regra geral da pobabilidade da união de dois eventos quaiquer como:

\[ P(A \cup B) = P(A) + P(B) - P(A \cap B) \]

Se \(A\) e \(B\) forem mutuamente exclusivos, a interseção entre eles será vazia (\(A \cap B =\varnothing\)) e, assim, essa probabiidade é zero. Nessa situação, a probabilidade de \(P(A \cup B)\) fica reduzida a uma regra particular para a adição de probabilidades de eventos mutuamente exclusivos:

\[ P(A \cup B) = P(A) + P(B) \]

Relembrando o que se denomina como regularidade estatística dos resultados :

\[ P\left(E\right)=\underset{n\to \infty }{lim}{\frac{F(E)}{n}} \]

# Função para simular uma população maior mantendo proporções
simPop <- function(tamanho_populacao) {
  # Proporções conforme a tabela
  prop <- data.frame(
    Curso = c("Matemática pura", "Matemática aplicada", "Estatística", "Computação"),
    Masculino = c(70, 15, 10, 20),
    Feminino = c(40, 15, 20, 10),
    Total = c(110, 30, 30, 30)
  )

  # Calculando as proporções relativas
  prop$propM <- prop$Masculino / prop$Total
  prop$propF <- prop$Feminino / prop$Total

  # Função para gerar amostra de acordo com as proporções
  gerar_amostra <- function(curso, propM, propF, total, tamanho_populacao) {
    n_curso <- round((total / sum(prop$Total)) * tamanho_populacao)
    sexo <- sample(c("M", "F"), n_curso, replace = TRUE, prob = c(propM, propF))
    data.frame(Curso = rep(curso, n_curso), Sexo = sexo)
  }

  # Gerando a população para cada curso
  populacao <- do.call(rbind, lapply(1:nrow(prop), function(i) {
    gerar_amostra(prop$Curso[i], prop$propM[i], prop$propF[i],
                  prop$Total[i], tamanho_populacao)
  }))

  return(populacao)
}

# Gerando uma população de 10.000 indivíduos
popSim <- simPop(100000)
table(popSim$Curso, popSim$Sexo)

##                      
##                           F     M
##   Computação           4905 10095
##   Estatística         10051  4949
##   Matemática aplicada  7564  7436
##   Matemática pura     19980 35020

# Selecionar uma amostra de 200 com reposição (simular a tabela)
ordem1=c("Matemática pura", "Matemática aplicada", "Estatística", "Computação")
ordem2=c("M", "F")
amostPop=popSim[sample(1:nrow(popSim), 200, replace = TRUE), ]
tab=table(factor(amostPop$Curso, levels = ordem1), factor(amostPop$Sexo, levels = ordem2))
tab=addmargins(tab)
colnames(tab)=c("M", "F", "Total")
rownames(tab)=c("Matemática pura (M)", "Matemática aplicada (A)","Estatística (E)","Computação (C)","Total")
tab

##                          
##                             M   F Total
##   Matemática pura (M)      68  48   116
##   Matemática aplicada (A)  13  12    25
##   Estatística (E)           8  20    28
##   Computação (C)           16  15    31
##   Total                   105  95   200

# Calcular a probabilidade de ser do sexo "Masculino" na amostra
pMasc<- mean(amostPop$Sexo == "M")
pMasc

## [1] 0.525

# Calcular a probabilidade de cursar "Matemática aplicada" na amostra
pMatAp <- mean(amostPop$Curso == "Matemática aplicada")
pMatAp

## [1] 0.125

# Calcular a probabilidade de cursar "Matemática aplicada" -E- ser do sexo "Masculino" na amostra
pMatAp_and_Masc <- mean(amostPop$Curso == "Matemática aplicada" & amostPop$Sexo == "M")
pMatAp_and_Masc

## [1] 0.065

# Calcular a probabilidade de cursar "Matemática aplicada" -OU- ser do sexo "Masculino" na amostra
pMatAp_or_Masc <- mean(amostPop$Curso == "Matemática aplicada" | amostPop$Sexo == "M")
pMatAp_or_Masc

## [1] 0.585

Exemplo: Uma população é composta por 20 pessoas que consomem o produto A, 30 pessoas que consomem o produto B e 50 pessoas que consomem o produto C . Um pesquisador de mercado seleciona aleatoriamente uma pessoa desta população. Sabendo que uma pessoa não consome mais de um produto ao mesmo tempo, qual a probabilidade de ter sido selecionada uma pessoa que consome os produtos A ou C?

Solução:

Definindo os eventos de interesse e as probabilidades associadas:

1- \(E_{A}=\text{consumidor do produto A}\): \(P(E_{A}=\frac{20}{100}\));
2- \(E_{B}=\text{consumidor do produto B}\): \(P(E_{B}=\frac{30}{100}\)); e,
3- \(E_{C}=\text{consumidor do produto C}\): \(P(E_{C}=\frac{50}{100}\)).

Pela regra geral da probabilidade da união de dois eventos quaiquer sabemos que:

\[ P(E_{A} \cup E_{C}) = P(E_{A}) + P(E_{C}) - P(E_{A} \cap E_{C}) \]

Como foi estabelecido no enunciado que uma pessoa não consome mais de um produto ao mesmo tempo (esses eventos são, portanto, mutuamente exclusivos: \(E_{A} \cap E_{C}=\varnothing\)) a probabilidade pedida será:

\[\begin{align*} P(E_{A} \cup E_{C}) & = P(E_{A}) + P(E_{C}) - P(E_{A} \cap E_{C}) \\ & = \frac{20}{10} + \frac{50}{100} - 0 \\ & = \frac{70}{100} \\ & = 0,70 \end{align*}\]

4.4 Probabilidade de eventos condicionados

Admita dois eventos definidos sobre o exprimento aleatório de se sortear uma carta de um baralho:

• \(A: \{A, 2,3,4,5,6,7,8,9,10,J,Q,K\}_{vermelho}\): cartas vermelhas (ouro e copas), e
• \(B: \{A, J, Q, K\}_{qualquer}\): cartas com figuras.

Se nosso interesse é agora determinar a probabilidade de um evento definido como uma vermelha e de figura ao mesmo tempo ou seja, uma carta que está simultaneamente nos conjuntos \(A\) e \(B\), estamos então interessados na probabilidade da interseção (conectivo \(\cap\)) desses dois eventos: \(P(A \cap B)\). Esse evento (interseção) acaba impondo restrições no espaço amostral inicial (todas as 52 cartas do baralho)

• Olhando-se por um prisma, podemos considerar que o espaço amostral agora é reduzido para \(A\): apenas as 26 cartas vermelhas: copas e ouro e, dentro desse novo espaço amostral, estamos interessados nos elementos \(B\): apenas as 4 cartas de figura: A, J, Q ou K.

A probabilidade do um evento \(B\) condicionada à ocorrência prévia do evento \(A\), pode ser entendida como a fração de \(B\) dentro de \(A\), ou seja:

\[ P(\text{foi sorteada uma carta vermelha, sortear-se uma figura})=\\ \frac{ \text{resultados favoráveis (número de cartas de figuras e vermelhas)}}{\text{resultados possíveis (número de cartas vermelhas)}}=\\ \frac{8}{26}=0,3076\\ \]

• Alternativamente, se olharmos por outro prisma, podemos considerar que o espaço amostral agora é reduzido para \(B\): apenas as 16 cartas de figuras e, dentro desse novo espaço amostral, estamos interessados nos elementos \(A\): apenas as 8 cartas vermelhas.

\[ P(\text{foi sorteada uma carta de figura, sortear-se uma carta vermelha})=\\ \frac{ \text{resultados favoráveis (número de cartas vermelhas e com figuras)}}{\text{resultados possíveis (número de cartas de figuras )}}=\\ \frac{8}{16}=0,50\\ \]

Dois eventos quaisquer \(A\) e \(B\) definidos sobre um experimento aleatório são ditos condicionados quando a ocorrência prévia de um deles impõe uma restrição no espaço amostral do segundo, alterando sua probabilidade original do outro. Ocorrência pode ser entendido alternativamente como uma informação adicional trazida a priori ao experimento, e que alterará a incerteza inicial que pairava sobre os possíveis resultados.

A probabilidade de um evento qualquer \(A\) condicionada a um segundo evento \(B\) é representada como \(P(A|B)\).

A barra vertical pode ser “lida” adotando-se termos correlatos que facilitam o entendimento da relação existente, tais como :

• probabilidade de \(A\) posto que ocorreu \(B\);
• probabilidade de \(A\) admitindo-se que ocorreu \(B\);
• probabilidade de \(A\) considerando-se que ocorreu \(B\),

Uma regra geral para o cálculo da probabilidade de dois eventos condicionados pode ser apresentada como:

\[\begin{align*} P(A|B) & = \frac{ P(A\cap B)}{ P(B)} \\ P(B|A) & = \frac{ P(B\cap A)}{ P(A)} \end{align*}\]

para \(P(B)>0\) e \(P(A)>0\) nas expressões acima.

Trazendo-se ao exemplo das cartas de baralho, as probabilidades marginais de aleatoriamente serem sorteadas cartas vermelhas, de figuras e vermelhas e de figuras são:

• uma carta vermelha: \(P(A)=26/52=0,50\)
• uma carta de figura é \(P(B)=16/52=0,3076\).
• uma carta vermelha e de figura é \(P(A \cap B) = 8/52=0,1538\)

\[ P(\text{foi sorteada uma carta vermelha, sortear-se uma figura}) -> P(B|A) =\\ \frac{ P(B\cap A)}{ P(A)}=\\ \frac{0,1538}{0,50}=\\ 0,3076\\ \]

A probabilidade marginal de se sortear uma carta de figura é 0,3076; todavia, com a informação a priori de que a carta sorteada foi uma carta vermelha, não se alterou.

\[ P(\text{foi sorteada uma carta de figura, sortear-se uma carta vermelha}) -> P(A|B) =\\ \frac{ P(A\cap B)}{ P(B)}=\\ \frac{0,1538}{0,3076}=\\ 0,50 \\ \]

Do mesmo modo, a probabilidade marginal de se sortear uma carta vermelha é 0,50; todavia, com a informação a priori de que a carta sorteada foi uma carta de figura, não se alterou.

Se P(B|A)=P(B) (naturalmente P(A|B)=P(A)) dizemos que os eventos A e B não são condicionados.

Exemplo: Consideremos a Tabela 4.3 que apresenta informações cruzadas do sexo dos alunos e seus respectivos cursos. Vamos definir os eventos Fem:sexo feminino e Est: cursar estatística. Como calcular a probabilidade condicionada de nosso evento de interesse P(Fem|Est) (a probabilidade de um aluno aleatoriamente escolhido ser do sexo feminino, dado que ele cursa estatística)?

\[\begin{align*} P(Fem|Est) & = \frac{ P(Fem \cap Est)}{ P(Est)} \\ & = \frac{20}{30} = \frac{2}{3} \end{align*}\]

Esse cálculo é facilmente entendido observando-se as celulas da distribuição de frequências na Tabela 4.3.

Exemplo: Considerem a Tabela 4.4 que relaciona a ida à praia de uma certa pessoa às condições climáticas do dia.

Table 4.4: Condicionamento de passeios à praia em relação às condições climáticas observadas

Dia	1	2	3	4	5	6	7	8	9	10
Foi à praia?	N	S	N	S	S	S	N	N	S	S
Fez sol?	N	S	N	S	N	S	S	N	S	S

Baseado nos dados coletados responda:

1- Qual a probabilidade dessa pessoa ir à praia?
2- Sabendo-se que fez Sol, qual a probabilidade dessa pessoa ir à praia?
3- Os eventos ir à praia e fazer Sol são independentes ou condicionados?

Da Tabela 4.4 extraímos as seguintes probabilidades:

\[\begin{align*} P(IP) & = \frac{6}{10}= 0,60 \\ P(FS) & = \frac{6}{10}= 0,60 \\ P(IP \cap FS) & = \frac{5}{10} \\ & = 0,50 \end{align*}\]

A partir delas podemos calcular a seguinte probabilidade condicionada:

\[\begin{align*} P(IP|FS) & = \frac{ P(IP \cap F)}{ P(FS)} \\ & = \frac{5}{6} \\ & = 0,83 \end{align*}\]

A probabilidade dessa pessoa ir à praia (\(P(IP)\)) é 0,60; mas quando faz Sol a probabilidade (\(P(IP|FS)\)) dela aumenta para 0,83.

Assim, os eventos \(IP\) e \(FS\) são condicionados: essa pessoa vai à praia 60% dos dias analisados; mas, quando faz sol, ela vai em 83% dos dias (a presença de Sol altera a probabilidade dela ir à praia).

Exemplo: Em uma cidade existem 15.000 usuários de telefonia, dos quais 10.000 possuem telefones fixos, 8.000 telefones móveis e 3.000 telefones fixos e móveis. Seja o experimento aleatório de uma operadora de telefone móvel selecionar uma pessoa dessa cidade para oferecer uma promoção do tipo “Fale Grátis de seu Móvel para seu Fixo”.

Responda:

1- Sorteando-se aleatoriamente um cliente dessa operadora, se soubermos antecipadamente que ele tem telefone móvel, qual a probabilidade de esse cliente tenha telefone fixo também?
2- Sabendo-se que ele tem telefone fixo, qual a probabilidade de ele tenha telefone móvel também?

O espaço amostral de todos esses possíveis eventos pode ser ilustrado pelo diagrama de Venn abaixo:

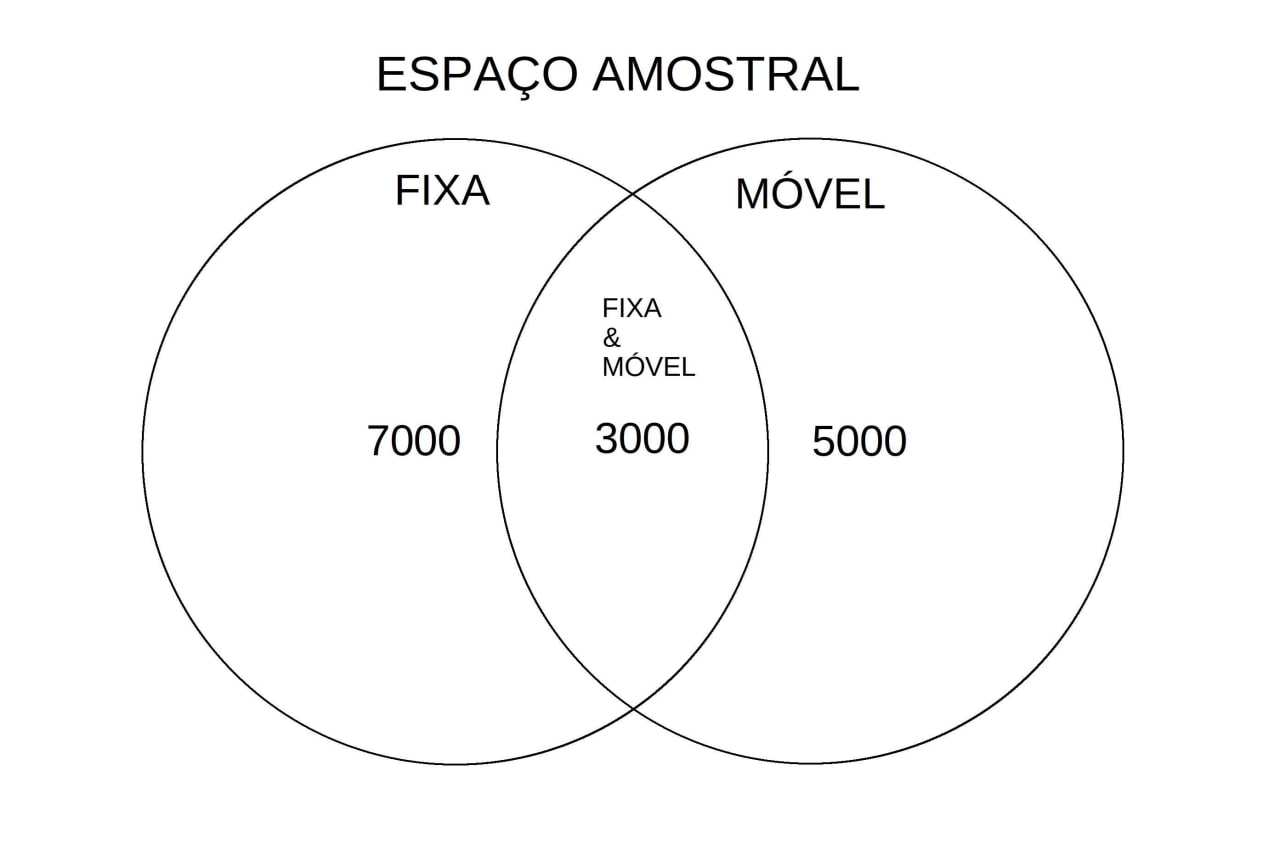
Figure 4.15: Diagrama de Venn do espaço amostral

Do diagrama apresentado na Figura4.15 podemos extrair imediatamente as probabilidades pedidas:

• \(P(F|M)\) (probabilidade de ter uma linha fixa sabendo que possui um telefone móvel); e,
• \(P(M|F)\) (probabilidade de ter uma linha móvel sabendo que possui um telefone fixo):

\[\begin{align*} P(F|M) & = \frac{n(MF)}{n(M)}\\ & =\frac{3000}{8000}\\ & = 0,375 \end{align*}\]

e

\[\begin{align*} P(M|F) & = \frac{n(MF)}{n(F)} \\ & =\frac{3000}{10000} \\ & = 0,300 \end{align*}\]

Mas também podemos calcular as probablidades do modo como explicado no começo desta sessão. Definindo-se os eventos \(F:\) telefone fixo e \(M:\) telefone móvel, a primeira pergunta pede \(P(F|M)\):probabilidade de ter um telefone fixo sabendo que ele tem um telefone móvel:

\[\begin{align*} P(F|M) & = \frac{P(F \cap M)}{P(M)} \\ & = \frac{ \frac{3000}{15000} }{\frac{8000}{15000} }\\ & = 0,375. \end{align*}\]

A segunda pede \(P(M|F)\): probabilidade de ter um telefone móvel sabendo que ele tem um telefone fixo:

\[\begin{align*} P(M|F) & = \frac{P(M \cap F)}{P(F)} \\ & = \frac{ \frac{3000}{15000} }{\frac{10000}{15000} } \\ & = 0,300 \end{align*}\]

Exemplo: Considere a Tabela 4.5 onde são expostos os resultados de uma pesquisa relacionada ao gosto pela prática de tênis entre alunos e alunas. Definindo-se os eventos \(A\):“gostar de tênis” e \(B\):“ser do sexo feminino”, calcule as probabilidade pedidas ao se sortear, aleatoriamente, uma das pessoas pesquisadas.

1- Qual a probabilidade de que goste de tênis (\(P(T)\))?
2- Qual probabilidade de que não goste de tênis (\(P(T^{c})\))?
3- Qual a probabilidade de que seja do sexo feminino ou goste de tênis: (\(P(F \cup T)\))?
4- Sabendo-se que foi sorteada uma aluna, qual a probabilidade de que goste de tênis (\(P(T|F))\)?
5- Verifique se os eventos \(T\): “gostar de tênis” e \(F\):“ser do sexo feminino” são condicionados ou independentes (\(P(T \cap F) \stackrel{?}{=} P(T) \times P(F)\)))

Table 4.5: Distribuição da quantidade de alunos segundo seu sexo e a preferência por tênis

	Sexo
Curso
	Masculino (M)	Feminino (F)	Total
Gostam de tênis (T)	400	200	600
Não gostam de tênis (NT)	50	50	100
Total	450	250	700

Exemplo: Imagine que um jogador está treinando cobranças de pênaltis. Historicamente a probabilidade de acertar uma cobrança, supondo que acertou a anterior é de 60%. Mas, se ele tiver errado a anterior a probabilidade de acertar cai para 30%. Construa a distribuição de probabilidades do número de acertos em 3 tentativas de cobrança.

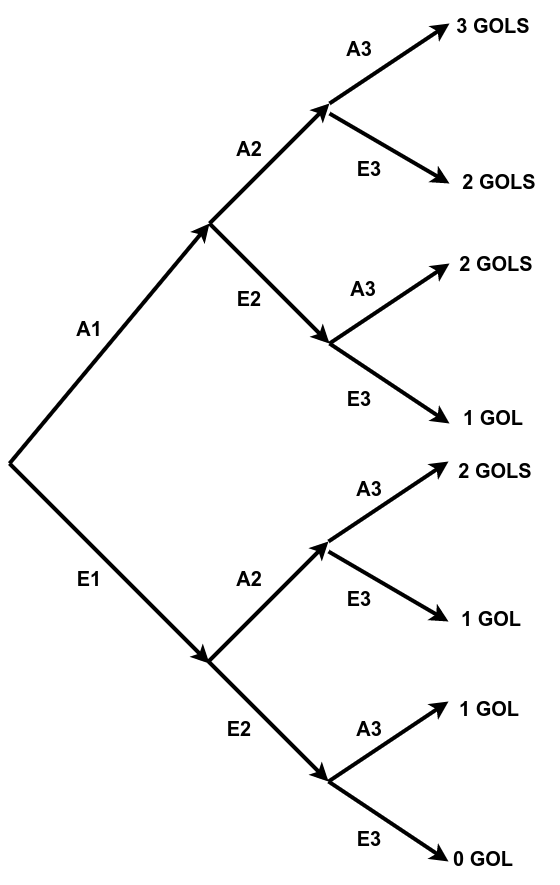
Figure 4.16: Diagrama em árvore das três repetições dependentes de um pênalti

A seguir vemos a cadeia de eventos necessária para que cada contagem de gols se verifique:

\[\begin{align*} \text{0 GOL} & = [E_{1} \cap E_{2} \cap E_{3}] \\ \text{1 GOL} & = \{ [A_{1} \cap E_{2} \cap E_{3}] \cup [E_{1} \cap A_{2} \cap E_{3}] \cup [E_{1} \cap E_{2} \cap A_{3}] \}\\ \text{2 GOLS} & = \{ [A_{1} \cap A_{2} \cap E_{3}] \cup [E_{1} \cap A_{2} \cap A_{3}] \cup [A_{1} \cap E_{2} \cap A_{3}] \}\\ \text{3 GOLS} & = [A_{1} \cap A_{2} \cap A_{3}] \\ \end{align*}\]

A probabilidade associada a cada contagem de gols será:

\[\begin{align*} P(\text{0 GOL}) & = P[E_{1} \cap E_{2} \cap E_{3}] \\ P(\text{1 GOL}) & = P\{ [A_{1} \cap E_{2} \cap E_{3}] \cup [E_{1} \cap A_{2} \cap E_{3}] \cup [E_{1} \cap E_{2} \cap A_{3}] \}\\ P(\text{2 GOLS}) & = P\{ [A_{1} \cap A_{2} \cap E_{3}] \cup [E_{1} \cap A_{2} \cap A_{3}] \cup [A_{1} \cap E_{2} \cap A_{3}] \}\\ P(\text{3 GOLS}) & = P[A_{1} \cap A_{2} \cap A_{3}] \\ \end{align*}\]

A partir do enunciado, podemos deduzir as probabilidades de cada um dos eventos:

\[\begin{align*} P(A_{1}) & = 0,50 \\ P(E_{1}) & = 0,50\\ P(A_{i+1}|A_{i}) & =0,60 \text{ logo, pelo complementar, } P(E_{i+1}|A_{i})=0,40\\ P(A_{i+1}|E_{i}) & =0,30 \text{ logo, pelo complementar } P(E_{i+1}|E_{i})=0,70\\ \end{align*}\]

\[\begin{align*} P(\text{0 GOL}) & = P[E_{1} \cap E_{2} \cap E_{3}] \\ P(\text{0 GOL}) & = P[E_{1}] \times P[E_{2}|E_{1}] \times P[E_{3}|E_{2}] \\ P(\text{0 GOL}) & = 0,50 \times 0,70 \times 0,70 \\ P(\text{0 GOL}) & = 0,245 \end{align*}\]

\[\begin{align*} P(\text{3 GOLS}) & = P[A_{1} \cap A_{2} \cap A_{3}] \\ P(\text{3 GOLS}) & = P[A_{1}] \times P[A_{2}|A_{1}] \times P[A_{3}|A_{2}] \\ P(\text{3 GOLS}) & = 0,50 \times 0,60 \times 0,60 \\ P(\text{3 GOLS}) & = 0,18 \end{align*}\]

\[\begin{align*} P(\text{1 GOL}) & = P\{ [A_{1} \cap E_{2} \cap E_{3}]\} + P\{ [E_{1} \cap A_{2} \cap E_{3}]\} + P\{[E_{1} \cap E_{2} \cap A_{3}]\}\\ P(\text{1 GOL}) & = P[A_{1}] \times P[E_{2}|A_{1}] \times P[E_{3}|E_{2}] +\\ & P[E_{1}] \times P[A_{2}|E_{1}] \times P[E_{3}|A_{2}] +\\ & P[E_{1}] \times P[E_{2}|E_{1}] \times P[A_{3}|E_{2}]\\ P(\text{1 GOL}) & = 0,50 \times 0,40 \times 0,70 +\\ & 0,50 \times 0,30 \times 0,40 +\\ & 0,50 \times 0,70 \times 0,30 \\ P(\text{1 GOL}) & =0,305 \end{align*}\]

\[\begin{align*} P(\text{2 GOLS}) & = P\{ [A_{1} \cap A_{2} \cap E_{3}]\} + P\{ [E_{1} \cap A_{2} \cap A_{3}]\} + P\{[A_{1} \cap E_{2} \cap A_{3}]\}\\ P(\text{2 GOLS}) & = P[A_{1}] \times P[A_{2}|A_{1}] \times P[E_{3}|A_{2}] +\\ & P[E_{1}] \times P[A_{2}|E_{1}] \times P[A_{3}|A_{2}] +\\ & P[A_{1}] \times P[E_{2}|A_{1}] \times P[A_{3}|E_{2}]\\ P(\text{2 GOLS}) & = 0,50 \times 0,60 \times 0,40 +\\ & 0,50 \times 0,30 \times 0,60 +\\ & 0,50 \times 0,40 \times 0,30 \\ P(\text{2 GOLS}) & =0,27 \end{align*}\]

4.5 Dependência e independência de eventos

Pela regra geral da probabilidade de dois eventos eventos condicionados:

\[\begin{align*} P(A|B) & = \frac{ P(A\cap B)}{ P(B)} \\ P(B|A) & = \frac{ P(B\cap A)}{ P(A)} \end{align*}\]

Como a probabilidade de interseção não se altera (\(P(A\cap B)=P(B\cap A)\)), podemos reescrever essas duas expressões:

\[\begin{align*} P(A \cap B) & = P(A|B) \times P(B) \\ P(A\cap B) & = P(B|A) \times P(A) \end{align*}\]

com \(P(B)>0\) e \(P(A)>0\) nas expressões acima.

Se os eventos \(A\) e \(B\) são guardam nenhuma relação de condicionamento eles são chamadas de eventos independentes. Equivale dizer que \(P(A|B)=P(A)\) (ou \(P(B|A)=P(B)\)), a probabilidade de \(A\) não se altera pela prévia ocorrência de \(B\) (ou a de \(B\) pelo de \(A\)).

Portanto, dois eventos são denominados independentes se, e somente se:

\[ P (A \cap B)= P(A) \times P(B) \]

Independência e correlação: se duas variáveis aleatórias são independentes não há associação de natureza alguma entre elas, inclusive a linear, um caso particular de correlação. Todavia uma correlação linear nula não implica em independência posto existirem várias outras formas outras de relacionamento (quadrática, cúbica, ).

Figure 4.17: Independência implica em ausência de qualquer tipo de associação (a recíproca não se aplica

4.5.1 Demonstração clássica de independência

Uma bolsa contém 5 bolas vermelhas e 5 azuis. Nós removemos uma bola aleatória da bolsa, registramos sua cor e a colocamos de volta na sacola. Em seguida, removemos outra bola aleatória da bolsa e registramos sua cor.

• Qual é a probabilidade de a primeira bola ser vermelha ?
  
• Qual é a probabilidade de a segunda bola ser azul?
  
• Qual é a probabilidade de a primeira bola ser vermelha e a segunda bola azul?
  
• A primeira bola retirada foi uma bola vermelha e a segunda bola azul; esses eventos foram independentes ?

Solução:

Probabilidade em se retirar uma bola vermelha em primeiro lugar:

Há 10 bolas das quais 5 são vermelhas . A probabilidade de se retirar uma bola vermelha será:

\[ P(1^{a} vermelha)= \frac{5}{10}= \frac{1}{2} \]

Probabilidade em se retirar uma bola azul em segundo lugar:

O enunciado do experimento assegura que após a retirada da primeira bola ela é devolvida ao sacola; por essa razão, ao se retirar a segunda bola, há novamente 10 bolas no total, das quais 5 são azuis. A probabilidade de se retirar uma bola azul será:

\[ P(2^{a} azul)= \frac{5}{10}= \frac{1}{2} \]

Probabilidade da primeira bola retirada ser vermelha e a segunda ser azul:

Ao se retirar duas bolas do sacola há quatro possíveis combinações de resultados. Nós podemos obter:

1- uma vermelha e depois outra vermelha;
2- uma vermelha e depois uma azul;
3- uma azul e depois uma vermelha; ou,
4- uma azul e depois outra azul;

Queremos saber a probabilidade do segundo resultado após termos obtido uma bola vermelha na primeira seleção.

Como existem 5 bolas vermelhas e 10 bolas no total, existem \(\frac{5}{10}\) possibilidades de obter uma bola vermelha primeiro.

Agora nós colocamos a primeira bola de volta, então há novamente 5 bolas vermelhas e 5 bolas azuis na sacola.

Portanto, há \(\frac{5}{10}\) possibilidades de obter uma segunda bola azul se a primeira bola for vermelha .

Isso significa que existem: \(\frac{5}{10} \times \frac{5}{10}= \frac{25}{100}\) possibilidades de se obter uma bola vermelha em primeiro lugar e uma bola azul em segundo.

Então, a probabilidade associada será de \(\frac{1}{4}\).

A primeira bola retirada foi uma bola vermelha e a segunda bola azul. Esses dois eventos são independentes?

Esses eventos serão independentes se, e somente se:

\[ P (A \cap B)= P(A) \times P(B) \]

\[\begin{align*} P(1^{a} vermelha) & = \frac{5}{10}= \frac{1}{2}\\ P(2^{a} azul) & = \frac{5}{10}= \frac{1}{2}\\ P(1^{a} vermelha,2^{a} azul) & = \frac{25}{100} = \frac{1}{4}\\ \end{align*}\]

Como \(\frac{1}{4}=\frac{1}{2} \times \frac{1}{2}\), os eventos são independentes.

Figure 4.18: Ilustração do experimento aleatório sob a condição de reposição

4.5.2 Demonstração clássica de dependência

E se, ao retirarmos a primeira bola, não a devolvêssemos ao sacola?

Admitamos agora que o enunciado de nosso problema passou a ser:

Uma bolsa contém 5 bolas vermelhas e 5 azuis. Nós removemos uma bola aleatória da bolsa, registramos sua cor e não a colocamos de volta na sacola. Em seguida, removemos outra bola aleatória da bolsa e registramos sua cor.

1- Qual é a probabilidade de a primeira bola ser vermelha ?
2- Qual é a probabilidade de a segunda bola ser azul?
3- Qual é a probabilidade de a primeira bola ser vermelha e a segunda bola azul?
4- A primeira bola retirada foi uma bola vermelha e a segunda bola azul; esses eventos foram independentes ?

Solução:

\(1^{a}\) Etapa: analisar todos os possíveis resultados

Probabilidade da primeira bola retirada ser vermelha e a segunda ser azul:

Ao se retirar duas bolas do sacola há quatro possíveis combinações de resultados. Nós podemos obter:

• uma vermelha e depois outra vermelha;
  
• uma vermelha e depois uma azul;
  
• uma azul e depois uma vermelha ; ou,
  
• uma azul e depois outra azul.

Queremos saber a probabilidade do segundo resultado após termos obtido uma bola vermelha na primeira seleção.

Como existem 5 bolas vermelhas e 10 bolas no total, existem \(\frac{5}{10}\) maneiras de obter uma bola vermelha primeiro.

Entretanto, nessa nova situação, nós não colocamos a primeira bola de volta, então haverá apenas 4 bolas vermelhas e 5 bolas azuis na sacola.

• Haverá \(\frac{4}{9}\) maneiras de obter uma segunda bola vermelha se a primeira bola for vermelha . Isso significa que existem: \(\frac{5}{10} \times \frac{4}{9}= \frac{20}{90}\) maneiras de se obter uma bola vermelha em primeiro lugar e uma bola vermelha em segundo. Então, a probabilidade associada será de \(\frac{2}{9}\);

• Haverá \(\frac{5}{9}\) maneiras de obter uma segunda bola azul se a primeira bola for vermelha . Isso significa que existem: \(\frac{5}{10} \times \frac{5}{9}= \frac{25}{90}\) maneiras de se obter uma bola vermelha em primeiro lugar e uma bola azul em segundo. Então, a probabilidade associada será de \(\frac{5}{18}\);

• Haverá \(\frac{5}{9}\) maneiras de obter uma segunda bola vermelha se a primeira bola for azul. Isso significa que existem: \(\frac{5}{10} \times \frac{5}{9}= \frac{25}{90}\) maneiras de se obter uma bola azul em primeiro lugar e uma bola vermelha em segundo. Então, a probabilidade associada será de \(\frac{5}{18}\).

• Haverá \(\frac{4}{9}\) maneiras de obter uma segunda bola azul se a primeira bola for azul. Isso significa que existem: \(\frac{5}{10} \times \frac{4}{9}= \frac{20}{90}\) maneiras de se obter uma bola azul em primeiro lugar e uma bola azul em segundo. Então, a probabilidade associada será de \(\frac{2}{9}\);

Resumo das probabilidades calculadas:

1 -uma vermelha e depois outra vermelha : \(\frac{2}{9}\);
2- uma vermelha e depois uma azul: \(\frac{5}{18}\);
3- uma azul e depois uma vermelha : \(\frac{5}{18}\); e,
4- uma azul e depois outra azul: \(\frac{2}{9}\).

\(2^{a}\) Etapa: analisar a possibilidade de se obter uma bola vermelha na primeira extração:

• uma vermelha e depois outra vermelha : \(\frac{2}{9}\);
  
• uma vermelha e depois uma azul: \(\frac{5}{18}\).

A probabilidade total de se obter uma bola vermelha na primeira extração será:

\[ P(1^{a} vermelha)= \frac{2}{9} + \frac{5}{18} = \frac{1}{2} \]

\(3^{a}\) Etapa: analisar a possibilidade de se obter uma bola azul na segunda extração:

• uma vermelha e depois uma azul: \(\frac{5}{18}\);
  
• uma azul e depois outra azul: \(\frac{2}{9}\).

A probabilidade total de se obter uma bola azul na segunda extração será:

\(P(2^{a} azul)= \frac{5}{18} + \frac{2}{9} = \frac{1}{2}\)

\(4^{a}\) Etapa: analisar a possibilidade de se obter uma bola vermelha e em seguida azul:

• uma vermelha e depois outra azul: \(\frac{5}{18}\);

\(5^{a}\) Etapa: Esses dois eventos são independentes?

Esses eventos serão independentes se, e somente se:

\[ P (A \cap B)= P(A) \times P(B) \]

\[\begin{align*} P(1^{a} vermelha) & = \frac{2}{9} + \frac{5}{18} = \frac{1}{2} \\ P(2^{a} azul) & = \frac{5}{18} + \frac{2}{9} = \frac{1}{2} \\ P(1^{a} vermelha,2^{a} azul) & = \frac{5}{18} \\ \end{align*}\]

Como \(\frac{5}{18} \neq \frac{1}{2} \times \frac{1}{2}\), os eventos não são independentes.

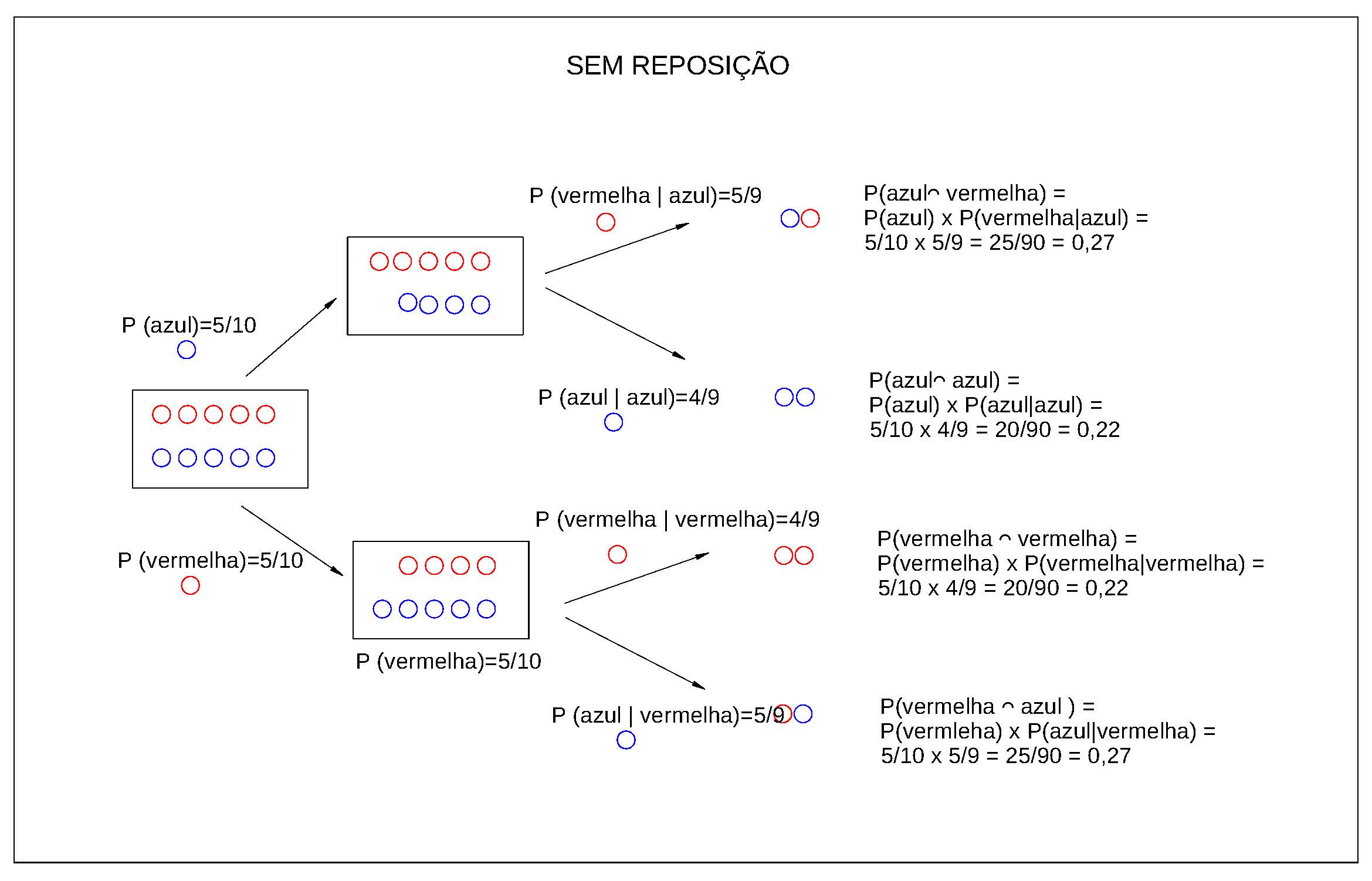
Figure 4.19: Ilustração do experimento aleatório sob a condição de não reposição

4.6 Probabilidade de eventos independentes (regra da cadeia)

Se \(E_{1}\), \(E_{2}\), …, \(E_{n}\) são eventos independentes entre si, então:

Para que isso se verifique, a independência entre cada um e todos os eventos deve se verificada. Numa situação de três eventos, por exemplo, teríamos que observar:

\[ P (E_{1} \cap E_{2})= P(E_{1}) \times P(E_{2}) \]

\[ P (E_{1} \cap E_{3})= P(E_{1}) \times P(E_{3}) \]

\[ P (E_{2} \cap E_{3})= P(E_{2}) \times P(E_{3}) \]

\[ P (E_{1} \cap E_{2} \cap E_{3} )= P(E_{1}) \times P(E_{2}) \times P(E_{3}) \]

Exemplo: considere o experimento aleatório de se lançar dois dados e obter o valor 1 no primeiro deles e 5 no segundo (defina os eventos \(E_{1}= \text{sair face 1}\) e \(E_{5}=\text{sair face 5}\)).

Solução:

Quando lançamos dois dados o resultado obtido em um deles (o valor numérico da face) não condiciona ou altera o resultado obtido no outro: os resultados são são independentes. Desse modo, sendo \(P(E_{1})=\frac{1}{6}\) e \(P(E_{5})=\frac{1}{6}\):

\[\begin{align*} P(E_{1} \cap E_{5}) & = \frac{1}{6} \times \frac{1}{6}\\ & = \frac{1}{36}. \end{align*}\]

Exemplo: Uma empresa que compra produtos de dois fabricantes diferentes (Fabricante 1 e Fabricante 2}) adquiriu 168 unidades do primeiro e 84 do segundo. Sabendo que 8 unidades fabricadas pelo primeiro fornecedor não atenderam às especificações e apenas 4 do segundo, verifique se o fato de uma amostra ter atendido às especificações independe de ter sido produzida pelo Fabricante 1.

Solução:

Para a primeira verificação pedida defina os eventos \(Fab1:\) ter sido produzida pelo Fabricante 1, \(Aprov:\) ter atendido às especificações e \(Fab2:\) ter sido produzida pelo Fabricante 2. Na sequência podemos calcular as seguintes probabilidades:

\[\begin{align*} P(Fab1) & = \frac{168}{252} \\ & = 0,6666 \\ P(Aprov) & = \frac{240}{252} \\ & = 0,9523 \\ P(Fab1 \cap Aprov) & = \frac{160}{252} \\ & = 0,6349 \end{align*}\]

Se o fato de uma amostra ter sido aprovada independe de ter sido produzida pelo Fabricante 1 então \(P(Aprov|Fab1) = P(Aprov)\):

\[\begin{align*} P(Aprov|Fab1) & = \frac{P(Aprov \cap Fab1)}{P(Fab1)} \\ & = \frac{0,6349}{0,6666} \\ & = 0,9523. \end{align*}\]

Como \(P(Aprov|Fab1) = P(Aprov)\), verifica-se que o fato de uma amostra aleatoriamente sorteada entre as peças do fabricante 1 não condiciona sua aprovação.

Exemplo: A probabilidade de um consumidor (\(C_{1}\)) ficar satisfeito com o desempenho de certa marca de produto é de 25%. A probabilidade de um outro consumidor (\(C_{2}\)) ficar satisfeito com a mesma marca é de 40%. Admitamos que os dois consumidores irão consumir o produto num mesmo momento e de forma independente (incomunicáveis). Qual a probabilidade de os dois consumidores ficarem satisfeitos simultaneamente?

Solução:

As probabilidades individuais dos consumidores 1 e 2 ficarem satisfeitos com o desempenho da marca do produto são:

\[\begin{align*} P(C_{1}) & = 0,25\\ P(C_{2}) & = 0,40 \end{align*}\]

A probabilidade de ambos ficarem satisfeitos, dado que o enunciado afirma que esses eventos são independente será:

\[\begin{align*} P(C_{1} \cap C_{2}) & = 0,25 \times 0,40\\ & = 0,10. \end{align*}\]

4.7 Teorema de Bayes

Figure 4.20: Thomas Bayes (1702 - 1761)

Admita o espaço amostral de um experimento baseado no sorteio aleatório de um estudante de uma escola, com dois possíveis resultados quanto ao sexo:

Figure 4.21: Espaço amostral

Considere agora um evento definido nesse espaço amostral como sendo ``ter um carro’’:

Figure 4.22: Espaço amostral

As interseções desse evento com os elementos do espaço amostral são:

Figure 4.23: Espaço amostral

Pela regra da probabilidade condicionada temos que

\[ P(C|F) = \frac{P(C \cap F)}{ P(F)}\\ P(C \cap F) = P(C|F) P(F) \]

e, de modo equivalente,

\[ P(C|M) = \frac{P(C \cap M)}{ P(M)}\\ P(C \cap M) = P(C|M) P(M) \]

A probabilidade de se ter um carro é dada pela regra da união de eventos que, nesse caso são disjuntos e assim:

\[ P(C) = P(C \cap M) \cup P(C \cap F)\\ P(C) = P(C|M) P(M) + P(C|F) P(F) \]

Sorteado aleatoriamente um estudante da escola verificou-se possuir um carro. Qual a probabilidade de que seja do sexo feminino (\(P(F|C)\))?

\[ P(F|C) = \frac{P(F \cap C)}{ P(C)}\\ P(F \cap C) = P(F|C) P(C) \\ \]

Pela igualdade \(P(C \cap F)=P(F \cap C)\):

\[ P(C \cap F) = P(C|F) P(F) \\ P(F \cap C) = P(F|C) P(C) \]

substituindo-se na expressão acima chega-se a:

\[\begin{align*} P(C \cap F) & =P(F \cap C)\\ P(C|F).P(F) & = P(F|C).P(C)\\ P(F|C) & = \frac{P(C|F)P(F)}{P(C)} \end{align*}\]

uma relação entre duas probabilidades inversamente condicionadas conhecida como Teorema de Bayes.

Adimita então serem dados:

• ``M’’: ser do sexo masculino: \(P(M)=0,65\);
• ``F’’: ser do sexo feminino: \(P(F)=0,35\).
• ``C’’: possuir um carro:
  • \(P(C|M)=0,30\)
  • \(P(C|F)=0,18\).

A probabilidade de se ter carro (\(P(C)\)) resulta de união de dois únicos e possíveis eventos condicionados ao sexo e disjuntos. Assim:

\[\begin{align*} P(C) & = P(C \cap M) \cup P(C \cap F)\\ P(C) & = [P(M).P(C|M)] \cup [P(F).P(C|F)] \\ P(C) & = [0,65 . 0,30] + [0,35 . 0,18] \\ P(C) & = 0,258\\ \end{align*}\]

e podemos calcular \(P(F|C)\):

\[\begin{align*} P(F|C) & = \frac{P(F).P(C|F)}{P(C)}\\ P(F|C) & = \frac{0,35 . 0,18 }{ 0,258}\\ P(F|C) & = 0,2442\\ \end{align*}\]

A probabilidade de que um estudante aleatoriamente sorteado nessa escola e sabendo-se a priori que possui um carro ser do sexo feminino é de 24,42%.

Para um espaço amostral mais amplo, de modo geral consideremos, inicialmente o diagrama da Figura 4.24 onde \(\Omega\) é o espaço amostral de um experimento aleatório qualquer:

Figure 4.24: Espaço amostral

Admita que \(E_{1}\), \(E_{2}\), \(E_{3}\) e \(E_{4}\) formem a partição do espaço amostral \(\Omega\) (seus elementos são mutuamente exclusivos) como exposto na Figura 4.25

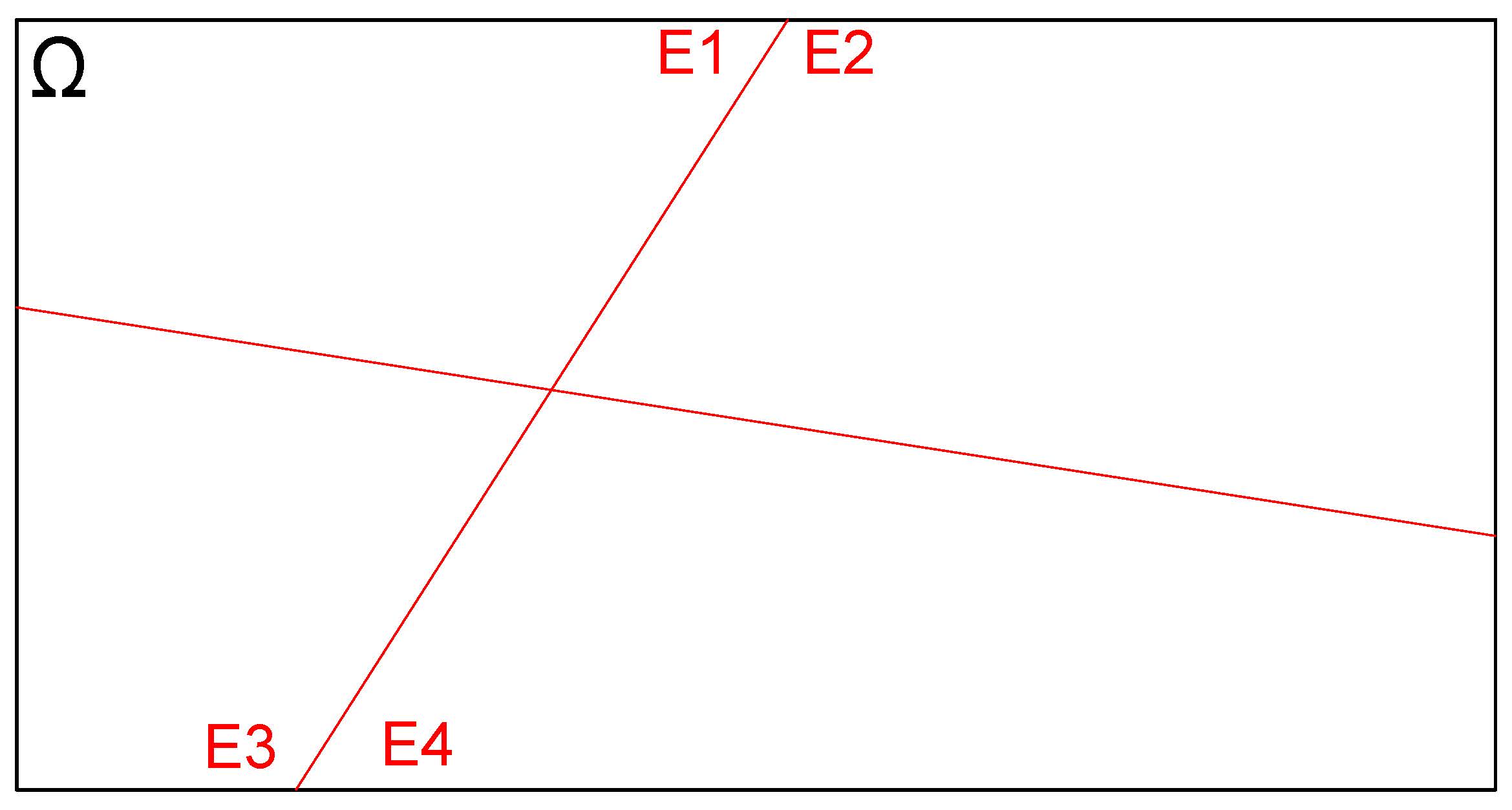
Figure 4.25: Espaço amostral e suas partições

E seja \(B\) um evento qualquer em \(\Omega\) como ilustrado na Figura 4.26

Figure 4.26: Evento definido sobre o espaço amostral

Delimitemos as interseções do evento \(B\) com as partições \(E_{1}\), \(E_{2}\), \(E_{3}\) e \(E_{4}\) do espaço amostral \(\Omega\), como ilustrado na Figura 4.27

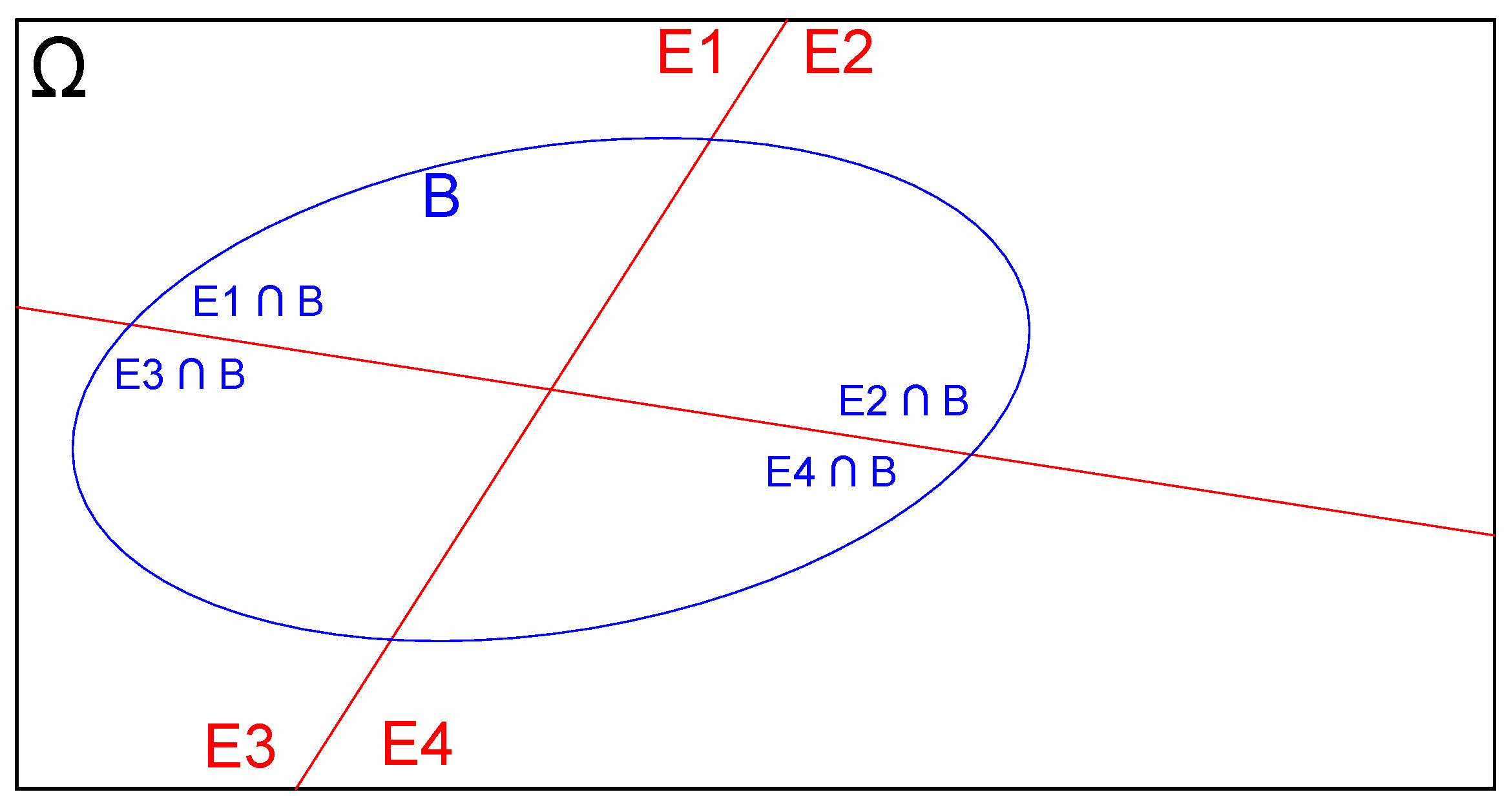
Figure 4.27: Interseções das partições do espaço amostral com o evento B

Isso pode ser estendido, em uma forma geral, para \(i=1, \dots, n\) partições como ilustrado na Figura 4.28

Figure 4.28: Interseções das n partições do espaço amostral com o evento B

Na representação esquemática da Figura 4.28 podemos identificar:

1- \(E_{1}\), \(E_{2}\), , \(E_{i}\), , \(E_{n}\) constituem-se em partições do espaço amostral \(\Omega\);
2- Todas as partições são mutuamente exclusivas: \(E_{i} \cap E_{j} = \varnothing\),\(\forall\) \(i \neq j\) (a interseção de quaisquer partições é vazia);
3- Sendo vazias as interseções entre quaisquer partições, o espaço amostral \(\Omega\) será a simples união de todas elas: \(\Omega = E_{1} \cup E_{2} \cup E_{3} \cup E_{4}\cup \dots \cup E_{i} \dots \cup E_{n}\); e,
4- B é um evento qualquer definido sobre as partições de \(\Omega\)

São conhecidas as probabilidades de ocorrência de cada um dos elementos do espaço amostral \(\Omega\):

\[ P(E_{1}); P(E_{2}); P(E_{3}); \dots;P(E_{i}); \dots; P(E_{n}) \]

e também as probabilidades do evento \(B\) condicionadas a cada elemento do espaço amostral:

\[ P(B|E_{1}); P(B|E_{2});\dots;P(B|E_{i});\dots; P(B|E_{n}) \]

A probabilidade de ocorrência do evento B é dada pela soma das probabilidades de cada uma de suas interseções com os elementos do espaço amostral \(\Omega\), uma vez que essas interseções são disjuntas entre si:

\[\begin{align*} P(B) & = P(E_{1} \cap B) \cup P(E_{2} \cap B) \cup \dots P(E_{i} \cap B) \cup \dots P(E_{n} \cap B) \\ P(B) & = \sum _{i=1}^{n}P\left({E}_{i}\cap B\right) \end{align*}\]

Pela Regra do produto de eventos condicionados, a probabilidade de ocorrência do evento B posto ter ocorrido um evento \(E_{i}\) é:

\[\begin{align*} P(B|E_{i}) & = \frac{P(E_{i}\cap B)}{P(E_{i})} \\ P(E_{i}\cap B) & = P(E_{i}) \times P(B|E_{i}) \end{align*}\]

com \(P(E) > 0\)

Aplicando-se na expressão anteriormente desenvolvida da probabilidade de ocorrência do evento B teremos:

\[\begin{align*} P(B) & = P(E_{1} \cap B) \cup P(E_{2} \cap B) \cup \dots \cup P(E_{i} \cap B) \cup \dots \cup P(E_{n} \cap B) \\ P(B) & = P(E_{1}) \times P(B|E_{1}) + P(E_{2}) \times P(B|E_{2}) + \\ & \dots +P(E_{i}) \times P(B|E_{i}) + \\ & \dots + P(E_{n}) \times P(B|E_{n}) \end{align*}\]

Portanto a probabilidade total do evento B em \(\Omega\) é dada pelo somatório:

\[ P(B) = \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\cdot P\left(B|{E}_{i}\right)\right] \]

Pela Regra do produto de eventos condicionados a probabilidade de ocorrência de um evento \(E_{i}\) posto ter ocorrido o evento \(B\) é:

\[\begin{align*} P(E_{i}|B) & = \frac{P(E_{i} \cap B)}{P(B)} \\ P(E_{i} \cap B) & = P(B) \times P(E_{k}|B) \\ P(B) & = \frac{P(E_{i}\cap B)}{P(E_{k}|B)} \end{align*}\]

com \(P(B) > 0\)

Pela igualdade dos dois modos de se expressar a probabilidade total do evento \(B\) desenvolvidos:

\[ P(B) = \frac{P(E_{i}\cap B)}{P(E_{i}|B)} \]

e

\[ P(B) = \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\cdot P\left(B|{E}_{i}\right)\right] \]

tem-se

\[ \frac{P(E_{i}\cap B)}{P(E_{i}|B)}=\sum _{i=1}^{n}\left[P\left({E}_{i}\right)\cdot P\left(B|{E}_{i}\right)\right] \]

Rearranjando-se em termos da expressão anterior para exprimir a probabilidade de ocorrência de um evento \(E_{i}\) posto ter ocorrido o evento \(B\) chegamos a:

\[ P(E_{i}|B) = \frac{P(E_{i}\cap B)}{\sum _{i=1}^{n}\left[P\left({E}_{i}\right)\cdot P\left(B|{E}_{i}\right)\right]} \]

Sendo

\[ P(E_{i} \cap B) = P(B) \times P(E_{i}|B) \]

a expressão anterior pode ser reescrita como:

\[ P(E_{i}|B) = \frac{ P(E_{i}) \times P(B|E{i}) }{ \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \]

uma forma mais geral do Teorema de Bayes.

O Teorema de Bayes é também chamado de Teorema da probabilidade a posteriori ao permitir que se calcule \(P(E_{i}|B)\) em termos da ocorrência \(P(B|E_{i})\)

É, de certo modo, uma conjugação do teorema na probabilidade total e da regra do produto de probabilidades.

O denominador:

\[ P(B)= \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] \]

é a denominada probabilidade marginal de ocorrência do evento \(B\) no espaço amostral \(\Omega\) composto por \(n\) elementos (partições).

Na expressão do Teorema de Bayes:

• \(P(E_{k}|B)\) é a denominada probabilidade a posteriori do evento \(E_{k}\) condicionada pela ocorrência anterior do evento B;
  
• \(P(E_{k})\) é a denominada probabilidade a priori do evento \(E_{k}\);
  
• \(P(B|E_{k})\) é a denominada probabilidade a posteriori do evento \(B\) condicionada pela ocorrência anterior do evento \(E_{k}\);
  
• \(P(E_{i})\) é a denominada probabilidade a priori de cada evento \(E_{i}\);
  
• \(P(B|E_{i})\) é a denominada probabilidade a posteriori do evento \(B\) condicionada pela ocorrência anterior de cada evento \(E_{i}\).

Exemplo: Constatou-se que o aumento nas vendas de um certo produto comercializado por uma empresa num mês pode ocorrer somente por uma das quatro causas mutuamente exclusivas a seguir:

1- ação de marketing;
2- propaganda;
3- flutuações na economia do país; ou,
4- efeitos sazonais.

A probabilidade de haver uma ação da empresa no mês focada para o marketing é de 40%; e para propaganda é de 30%; as probabilidades de ocorrerem flutuações na economia do país é de 20% e de efeitos sazonais é de 10%. Uma pesquisa mostrou que a probabilidade de haver um aumento nas vendas do produto devido a uma ação de marketing é de 7%; devido à publicidade, de 7,5%, por flutuações na economia do país, de 3% e por sazonalidade de 2%.

Em um determinado mês a empresa observou um considerável incremento nas vendas. Qual seria sua causa mais provável? Qual a probabilidade de incremento das vendas em um certo mês?

Inicialmente definimos um experimento aleatório como sendo “qual fato ocorreu no mês”.

Não sabemos qual fato ocorreu, mas sabemos que as possibilidades são apenas 4 (marketing, propaganda, flutuações na economia ou efeitos sazonais).

Podemos então conceber que esses fatos são elementos do espaço amostral do experimento aleatório: pois são eventos exaustivos e exclusivos: não pode ocorrer mais de um ao mesmo tempo e ao menos um ocorrerá.

Assim esse espaço amostral é composto pelos seguintes “elementos” e suas probabilidaes são tiradas do enunciado:

• \(E_{1}\) o elemento “Ação de marketing” \(\therefore \rightarrow\) \(P(E_{1})=0,40\);
  
• \(E_{2}\) o elemento “Ação de propaganda” \(\therefore \rightarrow\) \(P(E_{2})=0,30\);
  
• \(E_{3}\) o elemento “Flutuações na economia” \(\therefore \rightarrow\) \(P(E_{3})=0,20\); ou,
  
• \(E_{4}\) o elemento “Sazonalidade” \(\therefore \rightarrow\) \(P(E_{4})=0,10\).

Chamemos de \(B\) ao evento “ocorrer um incremento nas vendas”, um evento construído sobre os elementos do espeço amostral e que apresenta diferentes probabilidades a depender de qual elemento do espaço amostral ocorreu (a probabilidade de \(B\) está condicionada aos elementos do espaço amstral). Da leitura do enunciado extraímos as probabilidades de ocorrência de cada um dos eventos influenciadores:

As probabilidades condicionadas de ocorrer um incremento das vendas (\(B\)) pela ocorrência anterior de cada um dos elementos do espaço amostral (posto ter ocorrido o evento \(E_{i}\)) também são tiradas do enunciado:

• \(P(B|E_{1}) = 0,07\) ;
• \(P(B|E_{2}) = 0,075\);
  
• \(P(B|E_{3}) = 0,03\); e,
  
• \(P(B|E_{4}) = 0,02\).

Para responder à indagação do problema (“Qual a causa mais provável?”) podemos invertê-la e reformulá-la:

“Qual a probabilidade de ter ocorrido cada um dos quatro eventos (\(E_{1}\), \(E_{2}\), \(E_{3}\), \(E_{4}\)) posto (dado) ter ocorrido um incremento nas vendas?

Calculemos para cada um deles usando o Teorema de Bayes:

\[ P(E_{i}|B) = \frac{ P(E_{i}) \times P(B|E{i}) }{ \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \]

Probabilidade da empresa ter realizado uma ação de marketing, posto ter ocorrido um incremento nas vendas de seu produto:

\[\begin{align*} P(E_{1}|B) & = \frac{ P(E_{1}) \times P(B|E{1}) }{ \sum _{i=1}^{4}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \\ P(E_{1}|B) & = \frac{0,40 \times 0,07} { (0,40 \times 0,07) + (0,30 \times 0,075) +(0,20 \times 0,03) +(0,10 \times 0,02) } \\ P(E_{1}|B) & = 0,4786 \\ \end{align*}\]

Probabilidade da empresa ter realizado propaganda, posto ter ocorrido um incremento nas vendas de seu produto:

\[\begin{align*} P(E_{2}|B) & = \frac{ P(E_{2}) \times P(B|E{2}) }{ \sum _{i=1}^{4}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \\ P(E_{2}|B) & = \frac{0,30 \times 0,075} { (0,40 \times 0,07) + (0,30 \times 0,075) +(0,20 \times 0,03) +(0,10 \times 0,02) } \\ P(E_{2}|B) & = 0,3846 \end{align*}\]

Probabilidade da empresa ter ocorrido flutuações na economia, posto ter ocorrido um incremento nas vendas de seu produto:

\[\begin{align*} P(E_{3}|B) & = \frac{ P(E_{3}) \times P(B|E{3}) }{ \sum _{i=1}^{4}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \\ P(E_{3}|B) & = \frac{0,20 \times 0,03} { (0,40 \times 0,07) + (0,30 \times 0,075) +(0,20 \times 0,03) +(0,10 \times 0,02) } \\ P(E_{3}|B) & = 0,1026 \end{align*}\]

Probabilidade da empresa ter ocorrido efeitos sazonais, posto ter ocorrido um incremento nas vendas de seu produto:

\[\begin{align*} P(E_{4}|B) & = \frac{ P(E_{4}) \times P(B|E{4}) }{ \sum _{i=1}^{4}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \\ P(E_{4}|B) & = \frac{0,10 \times 0,02} { (0,40 \times 0,07) + (0,30 \times 0,075) +(0,20 \times 0,03) +(0,10 \times 0,02) } \\ P(E_{4}|B) & = 0,03419 \end{align*}\]

Respostas:

1- Os cálculos indicam que o evento mais provável pelo incremento das vendas observado naquele mês foi o de uma ação de marketing;
2- A probabilidade de incremento das vendas em um determinado mês como resultado dos quatro possíveis eventos indicados é o próprio denominador do Teorema de Bayes: 0,0585.

Exemplo: Considere 5 urnas, cada uma delas contendo 6 bolas. Duas dessas urnas (urnas tipo \(C_{1}\)) possuem 3 bolas brancas em seu interior. Duas outras (urnas tipo \(C_{2}\)) possuem 2 bolas brancas em seu interior e a última (urnas tipo \(C_{3}\)) possui 6 bolas brancas em seu interior (cf. Figura 4.29).

Figure 4.29: Cinco urnas cada uma com 6 bolas em cores de diferentes quantidades da cor branca

Escolhida aleatoriamente uma urna retira-se uma bola. Qual a probabilidade da urna escolhida ter sido a urna \(C_{3}\) sabendo-se que a bola retirada foi branca?

Desejamos determinar \(P(C_{3} | Branca)\)

Da leitura do enunciado extraímos as seguintes informações:

\[\begin{align*} P(C_{1}) & = \frac{2}{5} \\ P(C_{2}) & = \frac{2}{5} \\ P(C_{3}) & = \frac{1}{5} \\ P(Branca | C_{1}) & = \frac{1}{2} \\ P(Branca | C_{2}) & = \frac{1}{3} \\ P(Branca | C_{3}) & = 1 \end{align*}\]

\[\begin{align*} P(C_{3} | Branca) & = \frac{ P(C_{3}) \times P(Branca | C_{3}) }{ \sum_{i=1}^{3}\left[P\left({C}_{i}\right)\times P\left(Branca | {C}_{i}\right)\right] } \\ P(C_{3} | Branca) & = \frac{ 0,20 \times 1,00} { (0,40 \times 0,50 ) + (0,40 \times 0,33 ) +(0,20 \times 1,00)} \\ P(C_{3} | Branca) & = 0,375 \end{align*}\]

4.8 Teoremas da Teoria das probabilidades

4.8.1 Teorema 01

Se \(E\) é um evento num espaço discreto \(\Omega\), então \(P(E)\) é igual à soma das probabilidades de ocorrência de todos os elementos do espaço amostral que satisfazem ao evento de interesse \(E\) .

Sejam \(E_{1},E_{2},E_{3},\dots\) a sequência finita ou infinita de eventos que satisfazem ao evento de interesse \(E\). Assim, \(E = E_{1} \cup E_{2} \cup E_{3}...\). Como \(E_{1},E_{2},E_{3},\dots\) são eventos mutuamente exclusivos, pelo terceiro postulado das probabilidades teremos:

\[ P(E) = P(E_{1}) + P(E_{2}) + P(E_{3}) + ... \]

Exemplo: Lançamento de uma moeda duas vezes

Espaço amostral dos possíveis eventos (resultados): \(\Omega = \{(cara, cara), (cara, coroa), (coroa, cara), (coroa, coroa)\}\)

• Evento de interesse \(E\): obter ao menos uma cara
• Eventos que satisfazem: \(E_{1} =\{(cara, cara)\}\); \(E_{2} =\{(cara, coroa)\}\); \(E_{3} =\{(coroa, cara)\}\)

A probabilidade de \(E\) (\(P(E)\))será a soma das probabilidades dos eventos que o satisfazem:

\[ P(E) = P(E_{1}) + P(E_{2}) + P(E_{3}) = \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4} \]

4.8.2 Teorema 02

Se um experimento aleatório pode ter \(N\) resultados possíveis e equiprováveis e um evento \(E\) pode ter \(n\) resultados que o satisfazem, então \(P(E) = \frac{n}{N}\).

Sejam \(E_{1},E_{2},E_{3},\dots,E_{N}\) os resultados do espaço amostral \(\Omega\), cada um deles equiprovável (\(P(E_{i} =\frac{1}{N}\)). Se \(E\) é a união de \(n\) desses eventos mutuamente exclusivos, pelo terceiro postulado das probabilidades teremos:

\[\begin{align*} P(E) & = P(E_{1}) + P(E_{2}) + P(E_{3}) + ... P(E_{n}) \\ P(E) & = \frac{1}{N} + \frac{1}{N} +\frac{1}{N} +...+\frac{1}{N} \\ P(E) & = \frac{n}{N} \end{align*}\]

4.8.3 Teorema 03

Se \(E\) e \(E^{c}\) são eventos complementares no espaço amostra \(\Omega\) então \(P(E^{c}) = 1 - P(E)\).

Sendo os eventos \(E\) e \(E^{c}\) mutuamente exclusivos e também sendo \(E \cup E^{c} = \Omega\), considerando-se que \(P(\Omega) = 1\), pelos segundo e terceiro postulados tem-se:

\[\begin{align*} P(\Omega) & = 1 \\ 1 & = P(E \cup E^{c}) \\ 1 & = P(E) + P(E^{c}) \end{align*}\]

4.8.4 Teorema 04

\(P(\varnothing)=0\)

Sendo \(\Omega\) e \(\varnothing\) são mutuamente exclusivos e, como de acordo com a definição de um espaço vazio \(\Omega \cup \varnothing = \Omega\), pelo terceiro postulado tem-se:

\[\begin{align*} P(\Omega) & = P(\Omega \cup \varnothing)\\ P(\Omega) & = P(\Omega) + P(\varnothing)\\ P(\Omega) - P(\Omega) & = P(\varnothing)\\ P(\varnothing) & =0 \end{align*}\]

4.8.5 Teorema 05

Se \(A\) e \(B\) são eventos em um mesmo espaço amostral \(\Omega\) e \(A \subset B\) então \(P(A) \le P(B)\).

Se \(A \subset B\) então pode-se escrever: \(B = A \cup (A^{c} \cap B)\) (verifica-se pelo correspondente diagrama de Venn).

Como \(A\) e \(A^{c}\cap B\) são mutuamente exclusivos, pelo terceiro postulado tem-se:

\[\begin{align*} P(B) & = P(A) + P(A^{c}\cap B) \\ P(A) & = P(B) - P(A^{c}\cap B) \end{align*}\]

4.8.6 Teorema 06

A probabilidade de qualquer evento \(E\) em \(\Omega\) está compreendida entre \(0 \le P(E) \le 1\).

Estando \(\varnothing \subset E \subset \Omega\) e considerando-se o Teorema 5 tem-se:

\[ P(\varnothing) \le P(E) \le P(\Omega) \\ 0 \le P(E) \le 1 \]

4.8.7 Teorema 07

Para dois eventos quaisquer em \(\Omega\), \(A\) e \(B\) tem-se que: \(P( A \cup B ) = P(A) + P(B) - P(A \cap B)\).

Sejam as seguintes probabilidades para esses eventos mutuamente exclusivos:

• $P(A B) = a $;
  
• \(P(A \cap B^{c}) = b\); e,
  
• \(P(A^{c} \cap B) = c\).

\[\begin{align*} P ( A \cup B) & = a + b + c \\ P ( A \cup B) & = (a + b) + (c + d) - a \\ P ( A \cup B) & = P(A) + P(B) - P(A \cap B) \end{align*}\]

4.8.8 Teorema 08

Para três eventos quaisquer em \(\Omega\), \(A\), \(B\) e \(C\) tem-se que:

\[\begin{align*} P( A \cup B \cup C ) & = \\ & = P(A) + P(B) +P(C) - \\ & P(A \cap B) - P(A \cap C) - P(B \cap C) + \\ & P(A \cap B \cap C) \end{align*}\]

Escrevendo-se \(A \cup B \cup C\) como \(A \cup (B \cup C)\) e usando o Teorema 7 duas vezes (uma para \(P[A \cup (B \cup C)]\) e a outra para \(P( B \cup C)\) tem-se:

\[\begin{align*} P( A \cup B \cup C) & = P[ A \cup (B \cup C)] \\ P( A \cup B \cup C) & = P(A) + P( B \cup C) - P [A \cap (B \cup C)]\\ P( A \cup B \cup C) & = P(A) + P(B) + P(C) - P (B \cap C) - P [A \cap (B \cup C)] \end{align*}\]

Pela lei distributiva tem-se:

\[\begin{align*} P [A \cap (B \cup C)] & = P[ (A \cap B) \cup (A \cap C ) ]\\ P [A \cap (B \cup C)] & = P(A \cap B) + P(A \cap C) - P[ ( A \cap B) \cap (A \cap C)] \\ P [A \cap (B \cup C)] & = P(A \cap B) + P(A \cap C) - P( A \cap B \cap C) \end{align*}\]

Chega-se a :

\[\begin{align*} P( A \cup B \cup C ) & = \\ & P(A) + P(B) +P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) +\\ & P(A \cap B \cap C) \end{align*}\]