Capítulo 3 Introdução à estatística descritiva

Sobre o estudo da estatística por áreas nas quais, aparentemente, não se vislumbra sua utilidade trazemos o prefácio da tradução do livro de Jack Levin (Estatística aplicada às ciências humanas) por Sérgio Francisco Costa, ao dizer que o livro:

“[…] destina-se a um público muito específico: estudantes de Ciências Humanas, refúgio errôneo dos que fogem das equações e dos cálculos, pois que, embora humanas - e talvez por isso mesmo - não podemos prescindir das tão odiadas quantificações […]”

3.1 Análise exploratória

A análise exploratória de dados ( EDA: Exploratory Data Analisys , originalmente desenvolvida pelo matemático e estatístico norte-americano John Tukey na década de 1970) é usada para se investigar conjuntos de dados e resumir suas principais características, muitas vezes usando métodos de visualização de dados por gráficos e apresentação de tabelas.

Figure 3.1: John Tukey (1915-2000)

Habitualmente uma EDA envolve:

verificar quais são os tipos de variáveis presentes nos dados;
verificar os padrões de cada variável e eventuais associações entre duas ou mais delas; e,
apresentar os valores assumidos por cada uma das variáveis em formas resumidas como:
- resumos (sínteses) numéricos
- tabulares e
- gráficos.

3.2 Dados brutos, em rol, diagrama de ramos & folhas e de dispersão unidimensional

Consideremos os dados obtidos da medição das alturas em metros de 60 estudantes de uma determinada classe de um certo curso aqui na UEL:

alturas=c(1.63,1.67,1.47,1.64,1.66,1.73,2.00,1.62,1.65,1.56,1.65,1.85,1.73,
          1.78,1.82,1.68,1.67,1.83,1.72,1.71,1.73,1.67,1.66,1.95,1.76,1.73,
          1.77,1.68,1.65,1.64,1.66,1.68,1.61,1.73,1.72,1.83,1.69,1.84,1.66,
          1.78,1.54,1.74,1.56,1.66,1.56,1.62,1.55,1.86,1.44,1.67,1.76,1.79,
          1.75,1.41,1.65,1.58,1.93,1.57,1.71,1.58,0.1,3.68,0,NA)
alturas

##  [1] 1.63 1.67 1.47 1.64 1.66 1.73 2.00 1.62 1.65 1.56 1.65 1.85 1.73 1.78 1.82
## [16] 1.68 1.67 1.83 1.72 1.71 1.73 1.67 1.66 1.95 1.76 1.73 1.77 1.68 1.65 1.64
## [31] 1.66 1.68 1.61 1.73 1.72 1.83 1.69 1.84 1.66 1.78 1.54 1.74 1.56 1.66 1.56
## [46] 1.62 1.55 1.86 1.44 1.67 1.76 1.79 1.75 1.41 1.65 1.58 1.93 1.57 1.71 1.58
## [61] 0.10 3.68 0.00   NA

Garbage in, garbage out. Não são raras as vezes nas quais o relatório com os dados coletados em uma pesquisa apresentam uma série de erros. Não estamos a nos refeir aqui aos erros amostrais mas sim aos erros experimentais (não amostrais), aqueles decorrentes de dados coletados incorretamente, tais como aqueles resultantes de omissões na transcrição das informações, da leitura de instrumentos descalibrados ou de informações simplesmente não coletadas.

Denomina-se pré-processamento essa etapa de limpeza do conjunto de dados na qual busca-se corrigir de mdo extremamente criterioso esses problemas e, para tanto, um profundo conhecimento do objeto que está sendo pesquisado é necessário de modo a não serem liminarmente eliminados dados simplesmente por destoarem da alguma tendência (para essas tituações há ferramentas estatísticas apropriadas).

O conjunto original de dados ( dataset) refere-se a alturas de pessoas (estudantes ) e assim, tata-se de uma variável quantitativa e contínua e como tal será analisada. As omissões de informação “NA” ( not available) e as medidas transcritas com erros grosseiros (0 m; 0,10 m; 3,68 m) serão removidas.

Assim, o dataset será composto pelos dados abaixo:

alturas=c(1.63,1.67,1.47,1.64,1.66,1.73,2.00,1.62,1.65,1.56,1.65,1.85,1.73,
          1.78,1.82,1.68,1.67,1.83,1.72,1.71,1.73,1.67,1.66,1.95,1.76,1.73,
          1.77,1.68,1.65,1.64,1.66,1.68,1.61,1.73,1.72,1.83,1.69,1.84,1.66,
          1.78,1.54,1.74,1.56,1.66,1.56,1.62,1.55,1.86,1.44,1.67,1.76,1.79,
          1.75,1.41,1.65,1.58,1.93,1.57,1.71,1.58)
alturas

##  [1] 1.63 1.67 1.47 1.64 1.66 1.73 2.00 1.62 1.65 1.56 1.65 1.85 1.73 1.78 1.82
## [16] 1.68 1.67 1.83 1.72 1.71 1.73 1.67 1.66 1.95 1.76 1.73 1.77 1.68 1.65 1.64
## [31] 1.66 1.68 1.61 1.73 1.72 1.83 1.69 1.84 1.66 1.78 1.54 1.74 1.56 1.66 1.56
## [46] 1.62 1.55 1.86 1.44 1.67 1.76 1.79 1.75 1.41 1.65 1.58 1.93 1.57 1.71 1.58

Esse conjunto de dados certamente contém diversas informações acerca da altura dessas pessoas; todavia, da maneira como está apresentado a compreensão dessas informações fica bastante comprometida.

3.3 Apresentacao descritiva de dados na forma de resumos numericos

Esse modo de apresentação é chamado de dados brutos.

Com um pequeno refinamento, como pela simples ordenação desses dados (são medidas numéricas contínuas), algumas informações começam a se destacar:

sort(alturas)

##  [1] 1.41 1.44 1.47 1.54 1.55 1.56 1.56 1.56 1.57 1.58 1.58 1.61 1.62 1.62 1.63
## [16] 1.64 1.64 1.65 1.65 1.65 1.65 1.66 1.66 1.66 1.66 1.66 1.67 1.67 1.67 1.67
## [31] 1.68 1.68 1.68 1.69 1.71 1.71 1.72 1.72 1.73 1.73 1.73 1.73 1.73 1.74 1.75
## [46] 1.76 1.76 1.77 1.78 1.78 1.79 1.82 1.83 1.83 1.84 1.85 1.86 1.93 1.95 2.00

A interpretabilidade das informações trazidas por esses dados começa a ficar mais fácil como, por exemplo, as alturas:

mínima; e,
máxima dos estudantes.

A uma listagem de valores ordenada (de modo crescente ou decrescente) dá-se o nome de rol.

Além da apresentação elementar de algumas informações relacionadas aos dados brutos da amostra, tais como os valores mínimo e máximo observados, a estatística descritiva possui muitas outras ferramentas para condensar e expor a informação trazida pelos dados por meio resumos (sínteses) descritivos:

numéricos
tabulares
gráficos.

Resumos (sínteses) numéricos descritivos são quantidades que condensam variados aspectos relacionados aos valores dos dados.

As mais conhecidas sínteses numéricas podem ser agrupadas conforme o aspecto que expõem dos dados:

tendência central (posição): média (simples ou aritmética, geométrica, harmônica, anarmônica, quadrática, biquadrática), moda e mediana;
dispersão (variabilidade): absolutas (amplitude total, variância e desvio padrão) ou relativas (coeficiente de variação, unidades padronizadas); e,
subdivisão (separatrizes, quantis): mediana (50%), quartis (25%, 50%, 75%), decis (10%, ….90%) e percentis (1%….99%).

Uma medida de posição ou dispersão é dita resistente quando forem pouco afetadas pela alteração de uma pequena porção dos dados. A mediana é uma medida resistente, já a média e a variância não são.

3.3.1 Estimadores

Figure 3.2: Viés e variância

3.3.2 Medidas de tendência central (posição)

3.3.2.1 Média

Sejam $x_{1}, x_{2}, ..., x_{n}$ os $n$ valores assumidos pela variável $X$ (dados brutos). A média aritmética simples será dada por:

\[ \stackrel{-}{x}=\frac{\sum _{i=1}^{n}{x}_{i}}{n} \]

Algumas propriedades da média aritmética:

somando-se (ou subtraindo-se) cada um dos elementos do conjunto de dados por uma constante arbitrária qualquer $k$, a média aritmética ficará adicionada (ou subtraída) dessa essa constante $k$

alturas_ad=alturas+0.05

par(mfrow=c(1,2))

stripchart(alturas,method = "stack",  at=0.5, 
main="",pch = 20,
col="blue", cex=1, xlab="Alturas originais dos estudantes (m)", 
ylab="Quantidades observadas (un)")
abline(v=mean(alturas), col="red") 
text(mean(alturas)-0.2, 1, "Média=1,69 m", col = "red", srt=90) 

stripchart(alturas_ad,method = "stack",  at=0.5, 
main="",pch = 20,
col="blue", cex=1, xlab="Alt. dos estudantes (m) adic. de 5cm", 
ylab="Quantidades observadas (un)")
abline(v=mean(alturas_ad), col="red") 
text(mean(alturas_ad)-0.2, 1, "Média=1,74 m", col = "red", srt=90)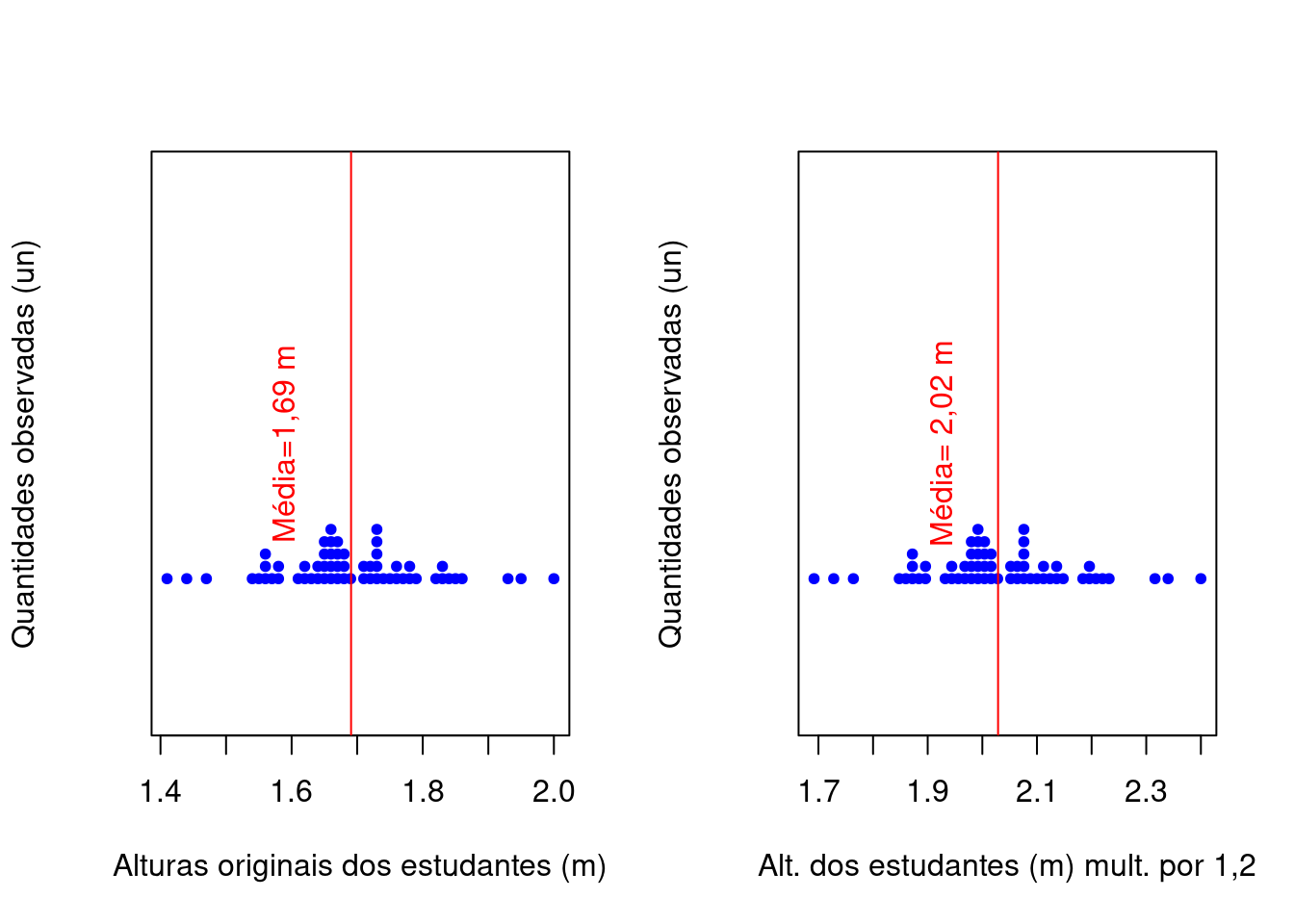

Figure 3.3: Mudanças na média pela adição (subtração) de uma constante $k=0.05$

multiplicando-se (ou dividindo-se) cada um dos elementos do conjunto de dados por uma constante arbitrária $k$, a média aritmética ficará multiplicada (ou dividida) por essa constante $k$

alturas_mult=alturas*1.2

par(mfrow=c(1,2))

stripchart(alturas,method = "stack",  at=0.5, 
main="",pch = 20,
col="blue",  xlab="Alturas originais dos estudantes (m)", 
ylab="Quantidades observadas (un)")
abline(v=mean(alturas), col="red") 
text(mean(alturas)-0.1, 1, "Média=1,69 m", col = "red", srt=90) 


stripchart(alturas_mult,method = "stack",  at=0.5, 
main="",pch = 20,
col="blue",  xlab="Alt. dos estudantes (m) mult. por 1,2", 
ylab="Quantidades observadas (un)")
abline(v=mean(alturas_mult), col="red") 
text(mean(alturas_mult)-0.1, 1, "Média= 2,02 m", col = "red", srt=90)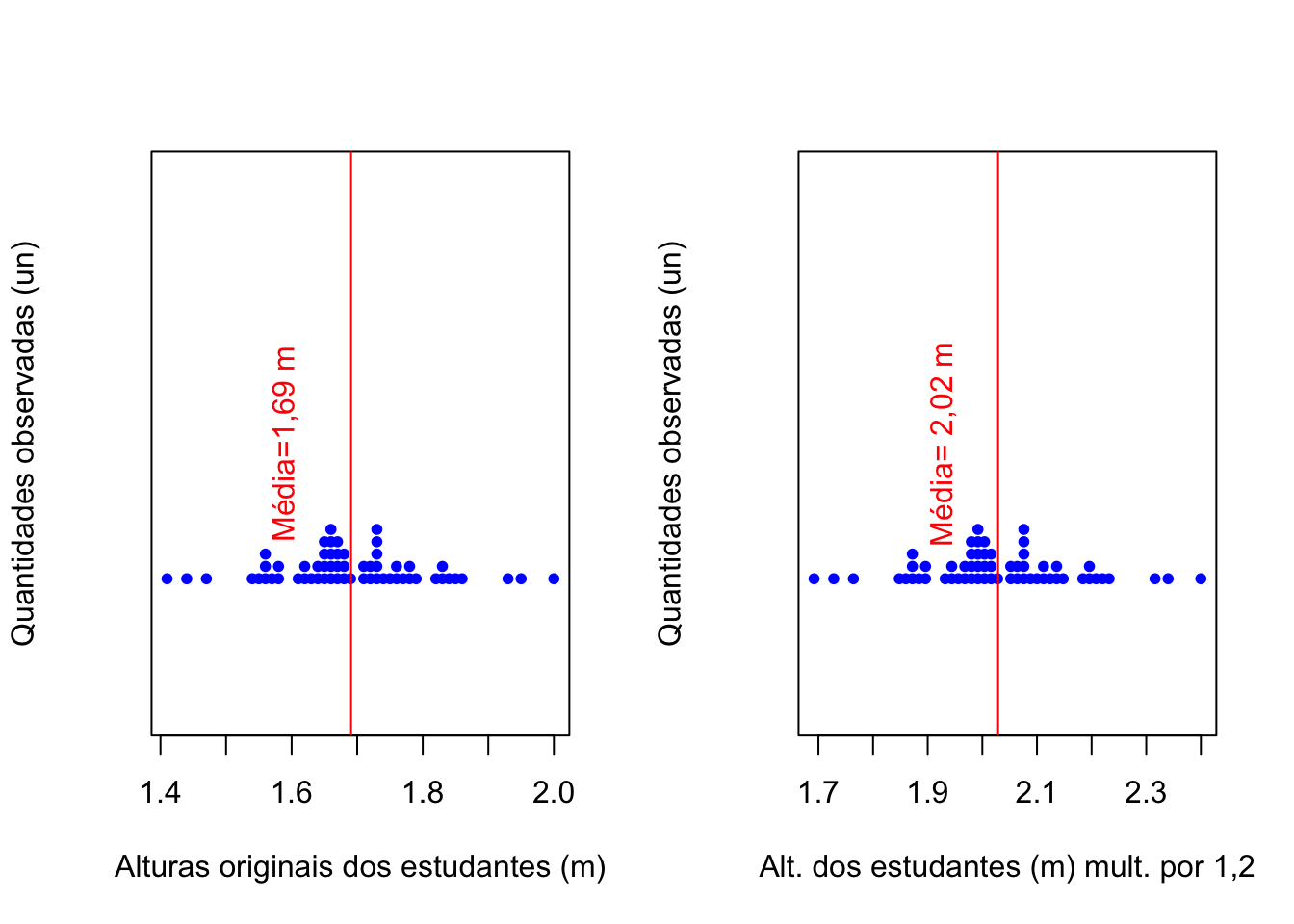

Figure 3.4: Mudanças na média pela multiplicação (divisão) de uma constante $k=1.2$

a soma dos desvios observados entre cada um dos valores assumidos pela variável $X$ e sua média $\stackrel{-}{x}$ é nula;
a soma dos quadrados dos desvios é mínima;
em uma distribuição de frequências, a soma dos produtos dos desvios entre a média o valor médio de cada uma das classes, pelas respectivas frequências é nula; e,
multiplicando-se (ou dividindo-se) todas as frequências de uma distribuição por uma constante arbitrária, a média aritmética não se altera.

Usando os dados das medidas das alturas dos 60 estudantes teremos o seguinte valor para a média:

round(mean(alturas),2)

## [1] 1.69

3.3.2.2 Moda

Moda é o valor que ocorre com maior frequência na amostra. Uma amostra pode se apresentar como:

unimodal;
bimodal;
plurimodal; ou,
amodal.

tab_alturas=table(alturas)

tab_alturas

## alturas
## 1.41 1.44 1.47 1.54 1.55 1.56 1.57 1.58 1.61 1.62 1.63 1.64 1.65 1.66 1.67 1.68 
##    1    1    1    1    1    3    1    2    1    2    1    2    4    5    4    3 
## 1.69 1.71 1.72 1.73 1.74 1.75 1.76 1.77 1.78 1.79 1.82 1.83 1.84 1.85 1.86 1.93 
##    1    2    2    5    1    1    2    1    2    1    1    2    1    1    1    1 
## 1.95    2 
##    1    1

barplot(tab_alturas,
        main="Valores observados da alturas dos estudantes",
        xlab="Altura (cm)",
        ylab="Quantidade observada (un)",
        ylim=c(0,6),
        col="blue",
        las=0, 
        hor="FALSE")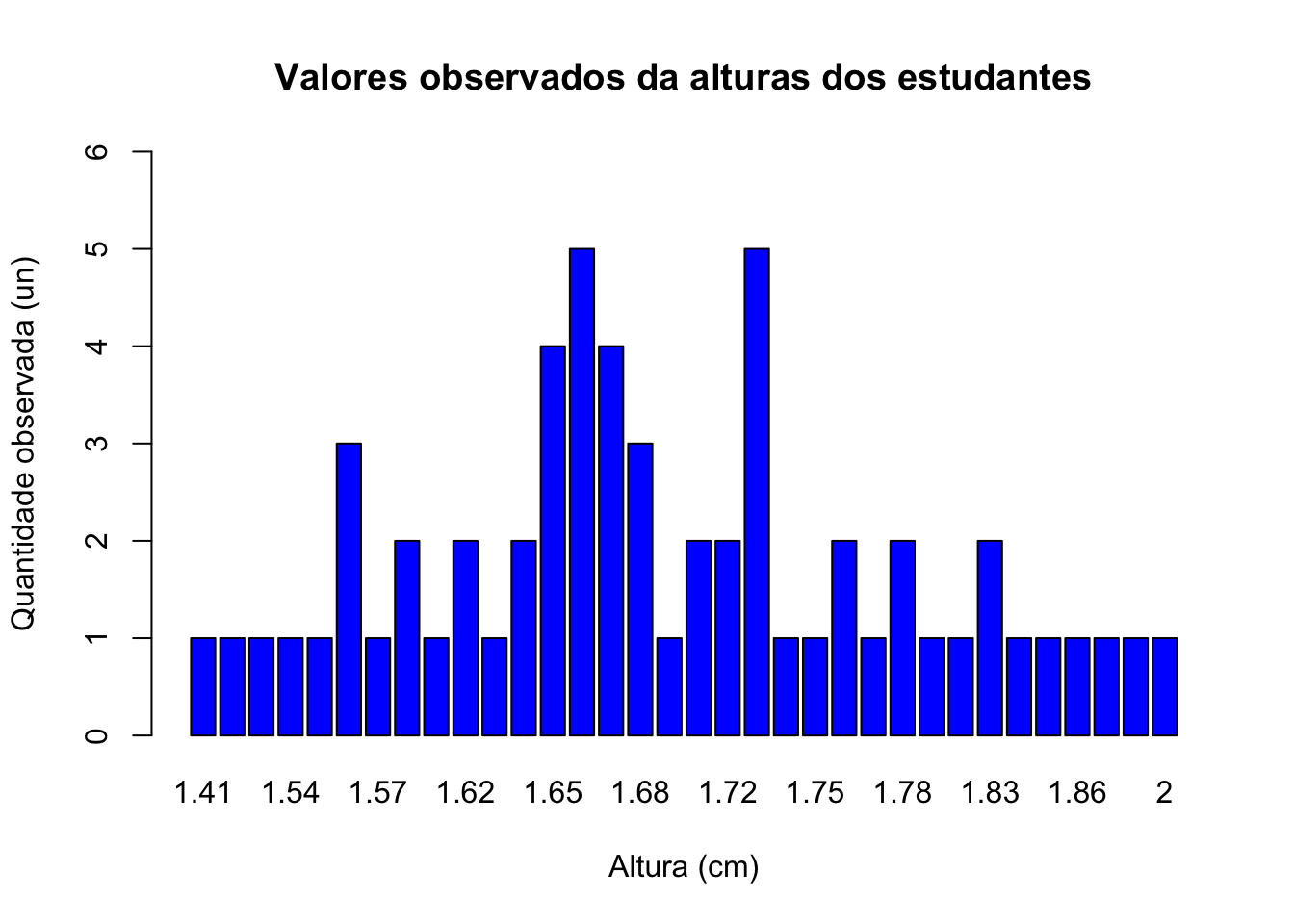

Figure 3.5: Bimodal: 1,66 m e 1,73 m

Usando os dados das medidas das alturas dos 60 estudantes teremos os seguintes valores para a moda:

# função em R para extrair a moda:

Modes <- function(x) {
  ux <- unique(x)
  tab <- tabulate(match(x, ux))
  ux[tab == max(tab)]
}

Modes(alturas)

## [1] 1.66 1.73

3.3.3 Medidas de dispersão (variabilidade)

O conhecimento de uma medida de tendência central nos provê uma informação útil mas incompleta. As medidas de dispersão nos ajudam a ter uma perspectiva melhor dos dados.

amplitude total dos dados;
desvio padrão (variância): é considerada a mais útil das medidas de dispersão;
coeficiente de variação; e,
unidades padronizadas.

Diferentes tipos quanto à dimensão (unidade):

medidas absolutas são aquelas expressas na mesma unidade de medida da variável do fenômeno estudado ($m;kg;\frac{R\$}{mês};\dots$);
medidas relativas são adimiensionais e assim podem ser usadas para se comparar a variabilidade de dois ou mais conjuntos de dados, mesmo quando as variáveis se refiram a diferentes fenômenos ou que sejam expressas, originalmente, em diferentes unidades.

3.3.3.1 Amplitude total dos dados

A amplitude total dos dados é a simples diferença entre o maior e o menor dos valores observados:

\[ A=x_{max} - x_{min} \]

3.3.3.2 Variância (e desvio padrão)

Sejam $x_{1}, x_{2}, ..., x_{n}$ os $n$ valores assumidos pela variável $X$. Dá-se o nome de desvios a contar da média as diferenças entre cada uma das observações e a média: $x_{i} - \stackrel{-}{x}$ com $i=1,2,...,n$.

Não é possível considerar a possibilidade de se adotar o valor médio desses desvios pois uma das propriedades da média é que a soma dos desvios em torno de si é nula.

\[ \stackrel{-}{d} = \frac{\sum _{i=1}^{n}\left(x_{i}-\stackrel{-}{x}\right)}{n} \] \[ \sum _{i=1}^{n}\left(x_{i}-\stackrel{-}{x}\right)=0 \]

constitui-se numa restrição linear dos desvios porque qualquer $n-1$ deles completamente determina o outro. Tampouco se considera a possibilidade de se adotar o valor médio desses desvios em módulo, pelas dificuldades teóricas em problemas de inferência.

\[ \stackrel{-}{d} = \frac{\sum _{i=1}^{n}\left|x_{i}-\stackrel{-}{x}\right|}{n} \]

Uma alternativa é adotar o valor médio do quadrado desses desvios.

\[ S^{2}=\frac{\sum _{i=1}^{n}\left(x_{i}-\stackrel{-}{x}\right)^{2}}{n-1} \]

ou,

\[ S^{2}=\frac{1}{(n-1)} \times \left[ \sum _{i=1}^{n} (x_{i}^{2}) - \frac{({\sum _{i=1}^{n}x_{i})}^{2} }{n}\right] \]

Diz-se que a variância amostral (variância ajustada) possui $(n-1)$ graus de liberdade, denotado pela letra grega $\nu$. A perda de um grau de liberdade deve-se à necessidade de se substituir a média populacional desconhecida ($\mu$) por sua estimativa amostral ($\stackrel{-}{x}$), deduzida a partir dos dados coletados.

Pode-se demonstrar que em razão dessa restrição a melhor estimativa para a variância populacional é obtida dividindo-se a soma dos quadrados dos desvios por $(n-1)$. Assim $S^{2}$ será um estimador não tendencioso para a variância amostral ao ser dividido por $(n-1)$.

IC.Na = function (N, n, mu, sigma) {
  dados=data.frame()
  plot(0, 0, 
       type="n", 
       xlim=c(sigma-0.1*sigma,sigma+0.1*sigma), 
       ylim=c(0,N), 
       bty="l",
       xlab="Desvio padrão", 
       ylab="Amostras extraídas", 
       main=paste0("Flutuação dos valores dos desvios padrão \nobtidos em ", N," amostras de tamanho ",n), 
       sub=paste0("A população de origem tem uma distribuição ~ N  (\u03bc:",mu," ; \u03c3:", sigma,")"))
  abline(v=sigma, col='darkgreen', lwd=2, lty=2)
for (i in 1:N) {
  x = rnorm(n, mu, sigma)
  media = mean(x)
  sd = sqrt(sum((x-mean(x))^2)/(n-1))
  sd_vies = sqrt(sum((x-mean(x))^2)/(n))
  temp=cbind(mu, media, sd, sd_vies)
  dados=rbind(dados, temp)
  plotx = c(sd)
  ploty = c(i,i)
  if ( sd < sigma) points(sd, i, col="blue",cex=1)+text(y=i+3,x=sd, labels=round(sd,3), cex=1, col='blue')
  else 
    points(sd, i, col="blue", cex=1)+text(y=i+3,x=sd, labels=round(sd,3), cex=1, col='blue') 
  plotx = c(sd_vies)
  ploty = c(i,i)
  if ( sd_vies < sigma) points(sd_vies, i, col="red",cex=1)+text(y=i+3,x=sd_vies, labels=round(sd_vies,3), cex=1, col='red')
  else 
    points(sd_vies, i, col="red", cex=1)+text(y=i+3,x=sd_vies, labels=round(sd_vies,3), cex=1, col='red') 
} 
abline(v=mean(dados$sd), col='blue', lwd=2, lty=2)
abline(v=mean(dados$sd_vies), col='red', lwd=2, lty=2)
}

IC.Na(N=100, n=15, mu=170, sigma=7)

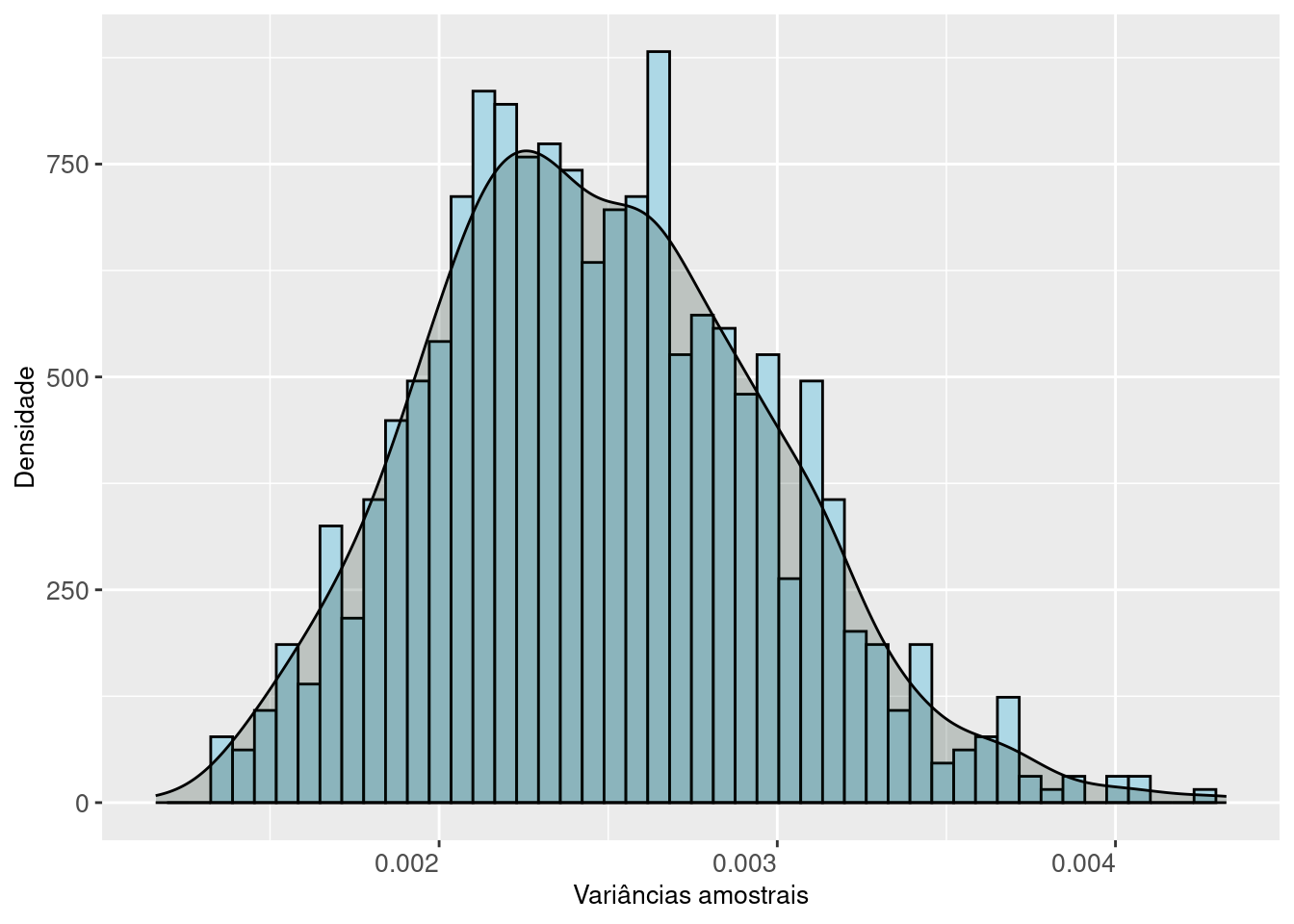
$Flutuação dos valores do desvio padrão obtidos pelo estimador não viesado (em azul) e pelo estimador viesado (em vermelho) para diversas amostras extraídas de uma mesma população distribuição $\sim N (\mu; \sigma)$ (em verde o desvio padrão populacional, em azul a média dos desvios padrão amostrais correta e em vermelho a estimada de modo viesado)$

Figure 3.6: Flutuação dos valores do desvio padrão obtidos pelo estimador não viesado (em azul) e pelo estimador viesado (em vermelho) para diversas amostras extraídas de uma mesma população distribuição $\sim N (\mu; \sigma)$ (em verde o desvio padrão populacional, em azul a média dos desvios padrão amostrais correta e em vermelho a estimada de modo viesado)

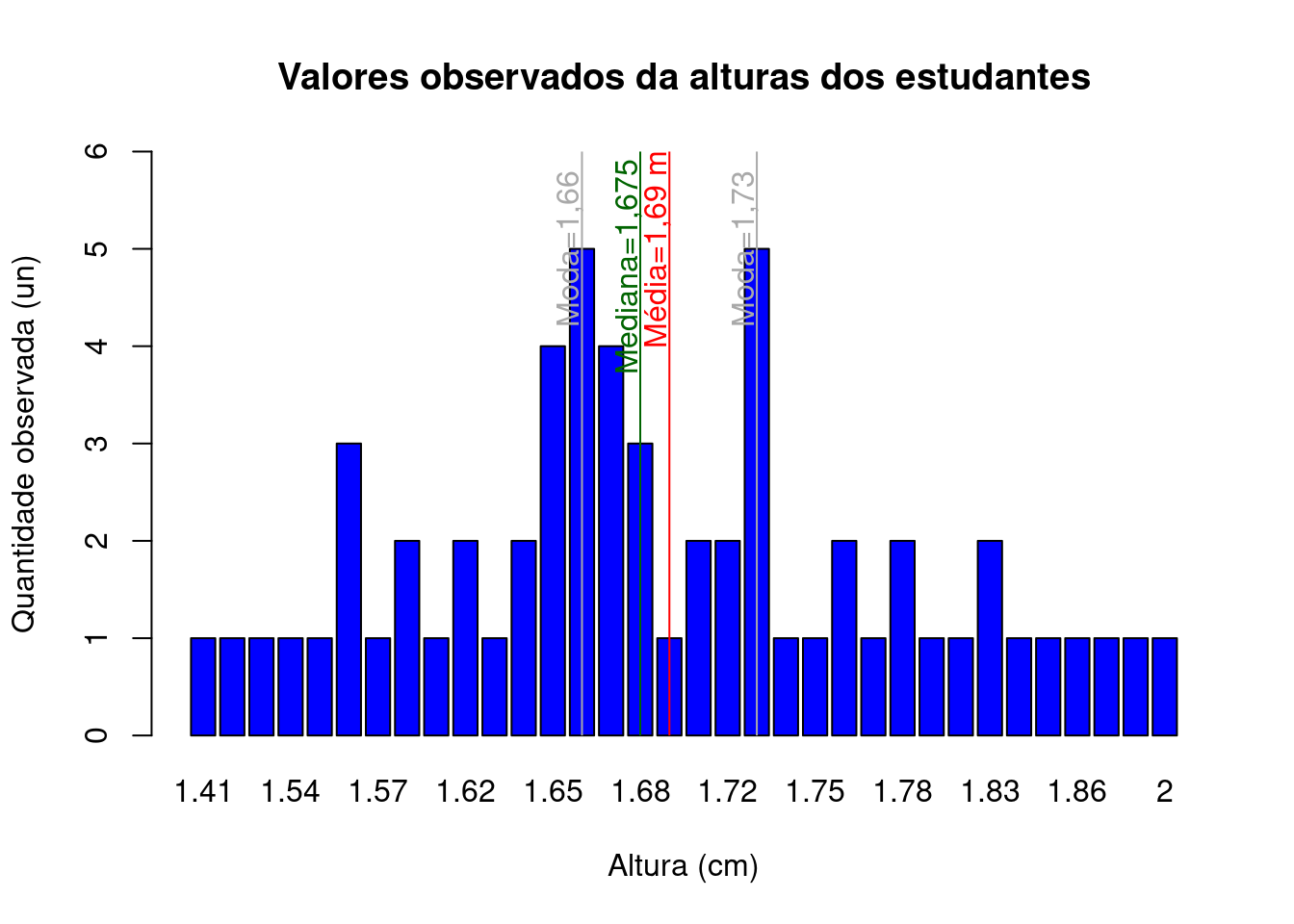
Figure 3.7: A distribuição das variâncias amostrais segue uma curva aproximada pela distribuição Qui-quadrado com (n-1) graus de liberdade

Uma medida de dispersão que apresenta a mesma unidade que a das observações originais é o desvio-padrão, definido como a raiz quadrada positiva da variância.

\[ S= \sqrt{\frac{\sum _{i=1}^{n}\left(x_{i}-\stackrel{-}{x}\right)^{2}}{n-1}} \]

Tanto a variância quanto o desvio padrão indicam, em média, qual será o erro (desvio) cometido ao tentar substituir cada observação pela medida resumo do conjunto de dados (média).

Usando os dados das medidas das alturas dos 60 estudantes teremos o seguinte valor para a variância (com unidade igual a $m^{2}$) e o desvio padrão (com unidade igual a $m$):

# Variãncia
var(alturas)

## [1] 0.0130809

# Desvio padrão
sd(alturas)

## [1] 0.1143718

Propriedades da variância:

somando-se (ou subtraindo-se) cada um dos elementos do conjunto de dados por uma constante arbitrária, a variância (e o desvio padrão) não se altera; e,
multiplicando-se (ou dividindo-se) cada um dos elementos do conjunto de dados por uma constante arbitrária, a variância ficará multiplicada (ou dividida) pelo quadrado dessa constante. O desvio padrão fica multiplicado (ou dividido) por essa constante

# Adicionando-se uma constante k=0.05
alturas_ad=alturas+0.05

# Variância não se altera
var_ad= var(alturas_ad)
var_ad

## [1] 0.0130809

# Multiplicando-se uma constante k=1.2
alturas_mult=alturas*1.2

# Variância fica multiplicada (dividida) pelo quadrado dessa constante)
var(alturas_mult)

## [1] 0.0188365

all.equal(var(alturas_mult), var(alturas)*(1.2^2))

## [1] TRUE

3.3.3.3 Coeficiente de variação.

O coeficiente de variação (uma medida adimensional) é dado pela razão do desvio padrão pela média:

\[ CV(\%)= 100\cdot(\frac{s}{\stackrel{-}{x}}) \]

Classificação da variabilidade a partir da medida do Coeficiente de variação
Classificação	Medida do Coeficiente de variação (CV %)
Baixo	CV ≤ 10%
Médio	10% ≤ CV ≤ 20%
Alto	20% ≤ CV ≤ 30%
Muito alto	CV ≥ 30%

3.3.4 Medidas de subdivisão (separatrizes)

Separatrizes (quantis) são medidas quantitativas que delimitam uma proporção de observações existentes em um conjunto de dados previamente ordenados com valores menores que ela.

Assim, se tomamrmos como exemplo a mediana, ela é dita uma separatriz (ou quantil) de 50% pois aproximadamente 50% dos dados de um conjunto possuem valores menores que ela.

Para se determinar qualquer separatriz necessitamos saber antes qual a posição que ela ocupa nos dados ordenados crescentemente: $x_{1}<x_{2}< \dots< x_{n}$:

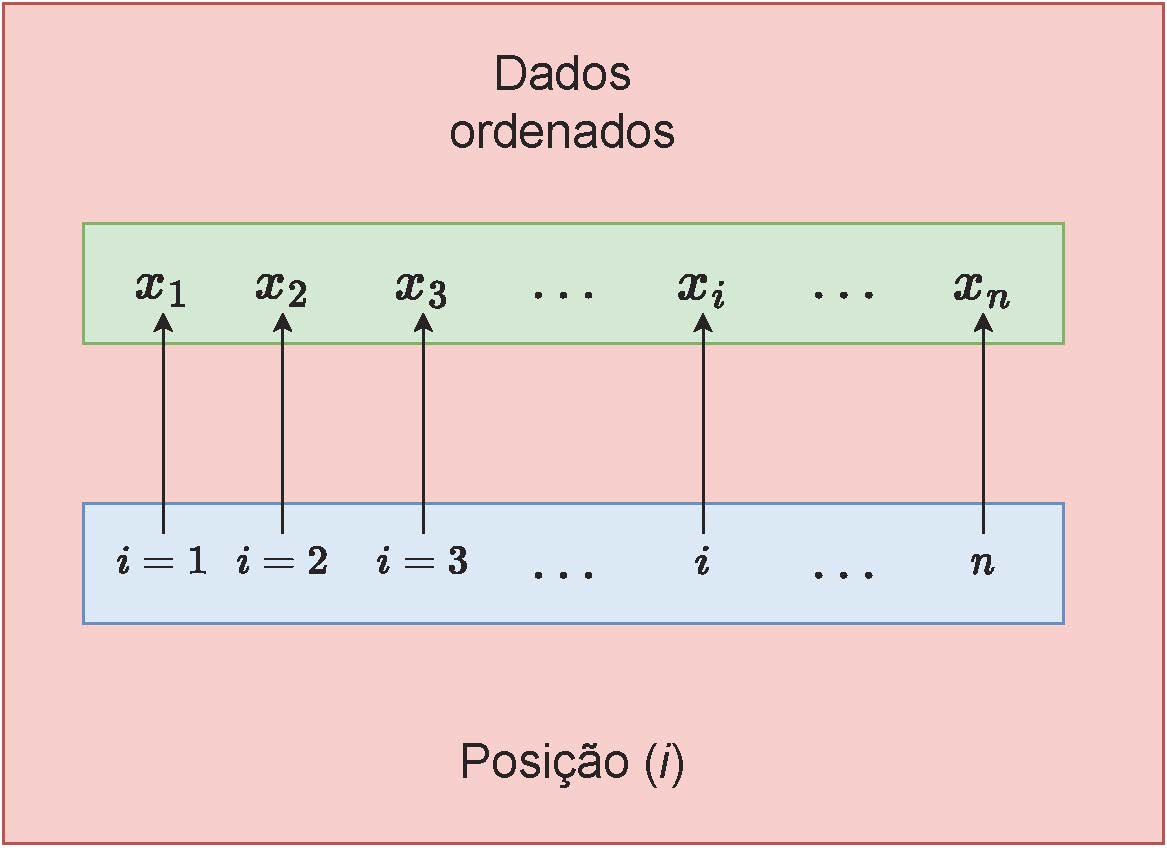
Figure 3.8: Entendendo a indexação de dados

De modo geral, um quantil de ordem $p$ (ou também $p-quantil$, indicado por $q_{p}$) é uma medida separatriz onde $p$ estabelece uma proporção qualquer (limitada no intervalo 0 < p < 1), tal que 100$p$% das observações sejam aproximadamente menores ou iguais que $q_{p}$. Desse modo, o valor $q_{p}$ de uma variável aleatória $X$ remete à medida da probabilidade:

\[ P(X=x | x\leq q_{p})=p \]

Para calcular o p-ésimo quantil de uma amostra de tamanho $n$, Hyndman e Fan (1996) estabeleceram:

\[j = (floor) [Np + m \rfloor]\],

em que:

$j$ = índice calculado
$N$ = tamanho da amostra
$p$ = percentil desejado (0 ≤ p ≤ 1)
$m$ = parâmetro específico do método

Tipo	Parâmetro m
1	0
2	0
3	-0.5
4	0
5	0.5
6	p
7	1 - p
8	(p+1)/3
9	p/4 + 3/8

Os quantis recebem diferentes nomes em função do modo como subdividem o conjunto de dados:

percentil (subdivisão em 100 partes): $p_{1}, \dots, p_{99}$
decis (subdivisão em 10 partes): $d_{10}, \dots, d_{90}$
quartis (subdivisão em 4 partes): $Q_{1}, \dots, Q_{3}$

Naturalmente que os valores de $p_{50}$, $d_{5}$ e $Q_{2}$ são os mesmos posto tratarem-se de separatrizes que subdividem os dados na mesma propoção (50%).

Os quantis mais informativos (e que por essa razão são usados para um importante gráfico que mais adiante será exposto em detalhes - Boxplot) são: \

1$^{o}$ Quartil ($q_{0,25}$): 25% dos dados possuem valores abaixo desse valor e 75% estão acima;
2$^{o}$ Quartil ou mediana ($q_{0,50}$): 50% dos dados possuem valores abaixo desse valor e 50% estão acima; e,
3$^{o}$ Quartil ($q_{0,75}$): 75% dos dados possuem valores abaixo desse valor e 25% estão acima.

Todavia a medicina utiliza para muitos propósitos os percentis como, por exemplo, as curvas de crescimento idade $versus$ altura.

De modo geral, para se calcular a posição L que um quantil qualquer de ordem p assume em um rol de dados há algumas regras empíricas:

\[ L_{p}=\frac{p}{100} \times (n)\\ L_{p}=\frac{p}{100} \times (n+1)\\ L_{p}=[\frac{p}{100} \times (n-1)]+1\\ \]

Onde:

p é a ordem do quantil em % (50% no caso mediana, por exemplo);
n é o número de dados do rol; e,
L é a posição do valor referente ao quantil desejado.

Os quartis calculados a partir das posições determinadas por essas regras aproximadamente subdividem o conjunto de dados em 25%, 50% e 75%.

Assim, para a determinação dos quartis pela primeira regra o valor de p seria:

para o primeiro quartil ($Q_{1}$): $L_{q_{0,25}}=\frac{25}{100} \times (n)$;
para o segundo quartil (a mediana ou $Q_{2}$): $L_{q_{0,50}}=\frac{50}{100} \times (n)$; ou,
para o terceiro quartil ($Q_{3}$): $L_{q_{0,75}}=\frac{75}{100} \times (n)$.

Novamente podemos nos deparar com duas situações possíveis para o valor calculado para a posição L qualquer que seja a regra:

se valor calculado da posição L for um inteiro, nessa posição encontraremos o valor referente ao quantil desejado;
se o valor calculado da posição L for fracionário, o valor desse quantil será determinado pela média entre os dois valores dos dados que estão nas posições imediatamente anterior e imediatamente posterior à posição L calculada.

Juntamente com as observações mínima ($x_{i}$) e máxima ($x_{n}$), o 1$^{o}$, 2$^{o}$ e 3$^{o}$ Quartis são importantes para se ter uma boa idéia da assimetria da distribuição dos dados.

Para uma distribuição simétrica (ou aproximadamente simétrica) deveremos observar (Distribuição Gaussiana):

a dispersão inferior: $q_{2} - x_{1} \approx x_{n} - q_{2}$ à dispersão superior ;
$q_{2} - q_{1} \approx q_{3} - q_{2}$; e,
$q_{1} - x_{1} \approx x_{n} - q_{3}$.

Para nosso conjunto de dados, segundo a regra empírica apresentada teremos as seguintes posições para determinação dos valores dos quartis:

para o primeiro quartil:

\[\begin{align*} L_{Q_{1}} & =\frac{p}{100} \times (n) \\ & =\frac{25}{100} \times (60) \\ & = 0,25*60 \\ & = 15 \end{align*}\]

para o segundo quartil:

\[\begin{align*} L_{Q_{2}} & =\frac{p}{100} \times (n) \\ & =\frac{50}{100} \times (60) \\ & = 0,5*60 \\ & = 30 \end{align*}\]

- para o terceiro quartil:

\[\begin{align*} L_{Q_{3}} & =\frac{p}{100} \times (n) \\ & =\frac{75}{100} \times (60) \\ & = 0,75*60 \\ & = 45 \end{align*}\]

E os quartis serão:

-$Q_{1}$=1,63
-$Q_{2}$=1,67
-$Q_{3}$=1,75

Em razão das variadas proposições existentes na literatura para se estabelecer os quantis o R apresenta 9 modos diferentes:

q <- c(0.25, 0.50, 0.75)
types <- c("1", "2", "3", "4", "5", "6", "7", "8", "9")

for(i in 1:9) {
  estimates <- quantile(alturas, q, type=i)
  cat(sprintf("Estimativas dos quartis segundo o método type %-2s => Q1: %.5f, Q2: %.5f, Q3: %.5f\n", 
              types[i], estimates[1], estimates[2], estimates[3]))
}

## Estimativas dos quartis segundo o método type 1  => Q1: 1.63000, Q2: 1.67000, Q3: 1.75000
## Estimativas dos quartis segundo o método type 2  => Q1: 1.63500, Q2: 1.67500, Q3: 1.75500
## Estimativas dos quartis segundo o método type 3  => Q1: 1.63000, Q2: 1.67000, Q3: 1.75000
## Estimativas dos quartis segundo o método type 4  => Q1: 1.63000, Q2: 1.67000, Q3: 1.75000
## Estimativas dos quartis segundo o método type 5  => Q1: 1.63500, Q2: 1.67500, Q3: 1.75500
## Estimativas dos quartis segundo o método type 6  => Q1: 1.63250, Q2: 1.67500, Q3: 1.75750
## Estimativas dos quartis segundo o método type 7  => Q1: 1.63750, Q2: 1.67500, Q3: 1.75250
## Estimativas dos quartis segundo o método type 8  => Q1: 1.63417, Q2: 1.67500, Q3: 1.75583
## Estimativas dos quartis segundo o método type 9  => Q1: 1.63437, Q2: 1.67500, Q3: 1.75562


import numpy as np

methods = [
   'inverted_cdf',
   'averaged_inverted_cdf',
   'closest_observation',
   'interpolated_inverted_cdf',
   'hazen',
   'weibull',
   'linear',
   'median_unbiased',
   'normal_unbiased',
   'nearest',
   'lower',
   'higher',
   'midpoint',
]
alpha = [0.25, 0.5, 0.75]
for m in methods:
   estimates = np.quantile(r.alturas, alpha, method=m)
   print(f"Estimativas dos quartis segundo o método {m:<25} => Q1: {estimates[0]:.4f}, Q2: {estimates[1]:.4f}, Q3: {estimates[2]:.4f}")

## Estimativas dos quartis segundo o método inverted_cdf              => Q1: 1.6300, Q2: 1.6700, Q3: 1.7500
## Estimativas dos quartis segundo o método averaged_inverted_cdf     => Q1: 1.6350, Q2: 1.6750, Q3: 1.7550
## Estimativas dos quartis segundo o método closest_observation       => Q1: 1.6300, Q2: 1.6700, Q3: 1.7500
## Estimativas dos quartis segundo o método interpolated_inverted_cdf => Q1: 1.6300, Q2: 1.6700, Q3: 1.7500
## Estimativas dos quartis segundo o método hazen                     => Q1: 1.6350, Q2: 1.6750, Q3: 1.7550
## Estimativas dos quartis segundo o método weibull                   => Q1: 1.6325, Q2: 1.6750, Q3: 1.7575
## Estimativas dos quartis segundo o método linear                    => Q1: 1.6375, Q2: 1.6750, Q3: 1.7525
## Estimativas dos quartis segundo o método median_unbiased           => Q1: 1.6342, Q2: 1.6750, Q3: 1.7558
## Estimativas dos quartis segundo o método normal_unbiased           => Q1: 1.6344, Q2: 1.6750, Q3: 1.7556
## Estimativas dos quartis segundo o método nearest                   => Q1: 1.6400, Q2: 1.6800, Q3: 1.7500
## Estimativas dos quartis segundo o método lower                     => Q1: 1.6300, Q2: 1.6700, Q3: 1.7500
## Estimativas dos quartis segundo o método higher                    => Q1: 1.6400, Q2: 1.6800, Q3: 1.7600
## Estimativas dos quartis segundo o método midpoint                  => Q1: 1.6350, Q2: 1.6750, Q3: 1.7550

Para grandes conjuntos de dados a diferença entre os quantis determinados sob esses diferentes modos será desprezível.

3.4 Padronizacao de dados (z-scores)

À conversão do valor assumido por uma variável em unidades de desvio padrão acima (ou abaixo) do valor médio de sua distribuição é dado o nome de padronização. Essa métrica permite comparações com outras, procedentes de outros fenômenos.

Para padronizar (achar o seu z-score Z) o valor de uma variável procede-se segundo a fórmula:

\[ Z=\frac{x_{i} - \stackrel{-}{x}}{s} \]

O valor $Z$ expressa quantos desvios esse dado está acima (ou abaixo) da média da distribuição.

Pelo Teorema de Tchebichev pode-se estimar a probabilidade mínima dos dados situados a certa distância de $k$ desvios da média dessa distribuição:

\[ P(|X-\mu|\ge k\sigma) \leq 1 - \frac{1}{k^{2}} \]

Assim, se $k=2$ ao menos 75% das observações devem estar entre a média e dois desvios padrões acima ou abaixo da média.

med=round(mean(alturas),2)
desv= round(sd(alturas),2)

No exemplo das alturas dos estudantes temos a média de 1.69 m e um desvio padrão de 0.11 m. Assim, ao menos 75% das alturas deverão estar entre 1.47 m e 1.91 m.

sort(alturas)

##  [1] 1.41 1.44 1.47 1.54 1.55 1.56 1.56 1.56 1.57 1.58 1.58 1.61 1.62 1.62 1.63
## [16] 1.64 1.64 1.65 1.65 1.65 1.65 1.66 1.66 1.66 1.66 1.66 1.67 1.67 1.67 1.67
## [31] 1.68 1.68 1.68 1.69 1.71 1.71 1.72 1.72 1.73 1.73 1.73 1.73 1.73 1.74 1.75
## [46] 1.76 1.76 1.77 1.78 1.78 1.79 1.82 1.83 1.83 1.84 1.85 1.86 1.93 1.95 2.00

# Duas observações menores que 1,47m e trẽs maiores que 1,91m.
# Assim, 54 observações dentro do intervalo, equivalendo a 91,66% do total.

3.5 Medidas de forma (assimetria & curtose)

Quando analisamos o histograma (a representação gráfica da distribuição das frequências dos valores agrupados em classes) de uma determinada variável, não é muito comum que ele se mostre simétrico tal como seria se os dados fossem distribuídos de modo exatamente Normal.

Ao observarmos que a cauda se mostra mais alongada para a direita (indicativo da existência de uma quantidade maior de dados com grandes valores, arrastando a média para a direita: moda $<$ mediana $<$ média) diz-se que a distribuição é assimétrica à direita. Na situação oposta (moda $>$ mediana $>$ média) diz-se que ela é assimétrica à esquerda.

a=rbeta(10000,5,2)
c=rbeta(10000,5,5)
b=rbeta(10000,2,5)

par(mfrow=c(1,3))
hist(a, 
     xlab="Valores",col = 'lightblue',
     ylab="Frequência",
     main="Assimetria à esq.")
hist(c, 
     xlab="Valores",col = 'lightblue',
     ylab="Frequência",
     main="Relativa simetria")
hist(b, 
     xlab="Valores",col = 'lightblue',
     ylab="Frequência",
     main="Assimetria à dir.")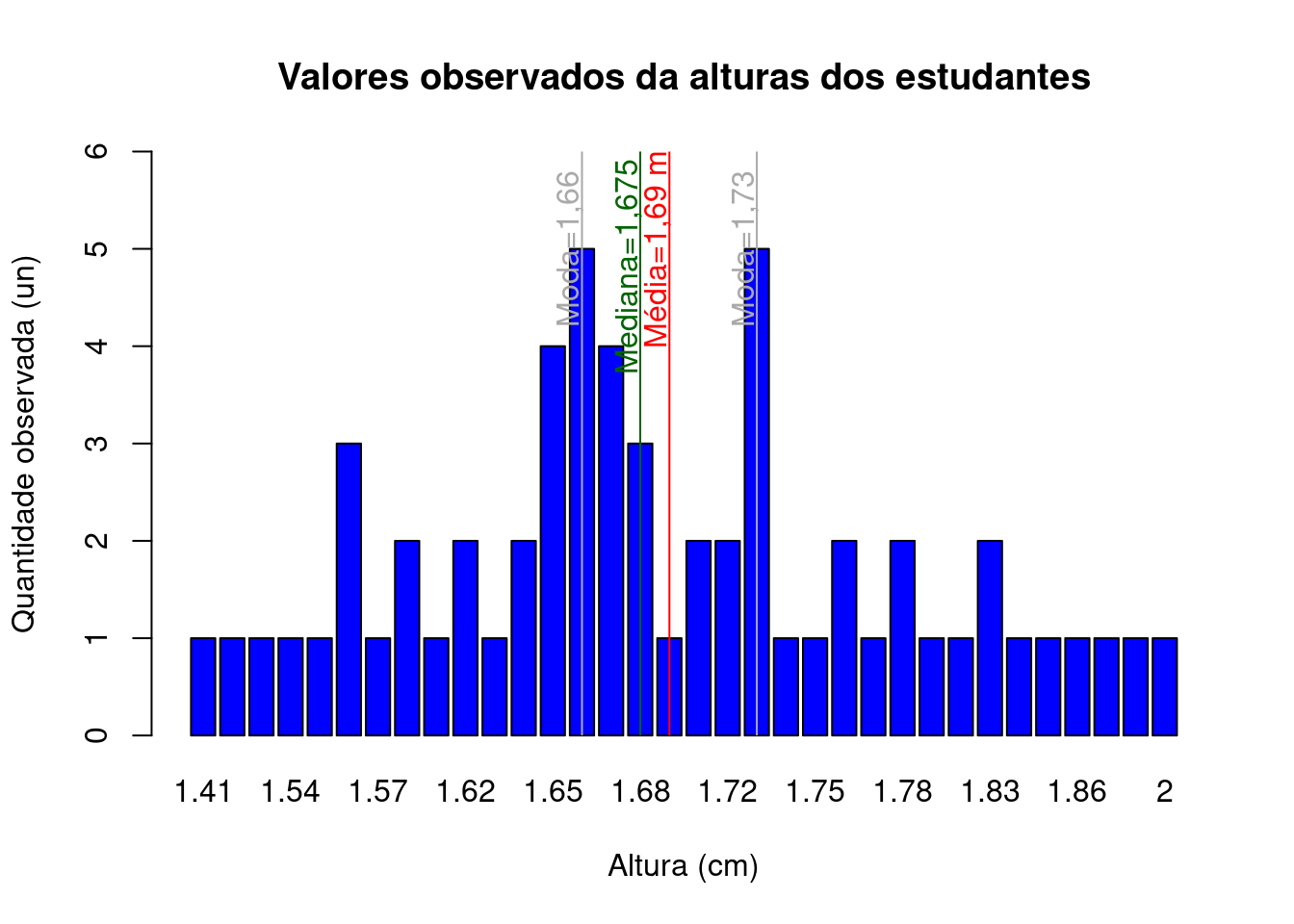

Figure 3.9: Diferentes formas na distribuição dos dados

De modo assemelhado, o histograma pode denotar uma forma mais plana ou menos aguda, onde um cume mostra-se mais destacado.

Nesse aspecto da forma, uma variável com distribuição Gaussiana apresentaria uma curva a que denominamos mesocúrtica. Distribuições com um aspecto mais plano são denominadas de platicúrticas e as com um cume agudo são denominadas leptocúrticas.

A curtose é uma medida da agudeza da distribuição dos dados em relação à distribuição Gaussiana.

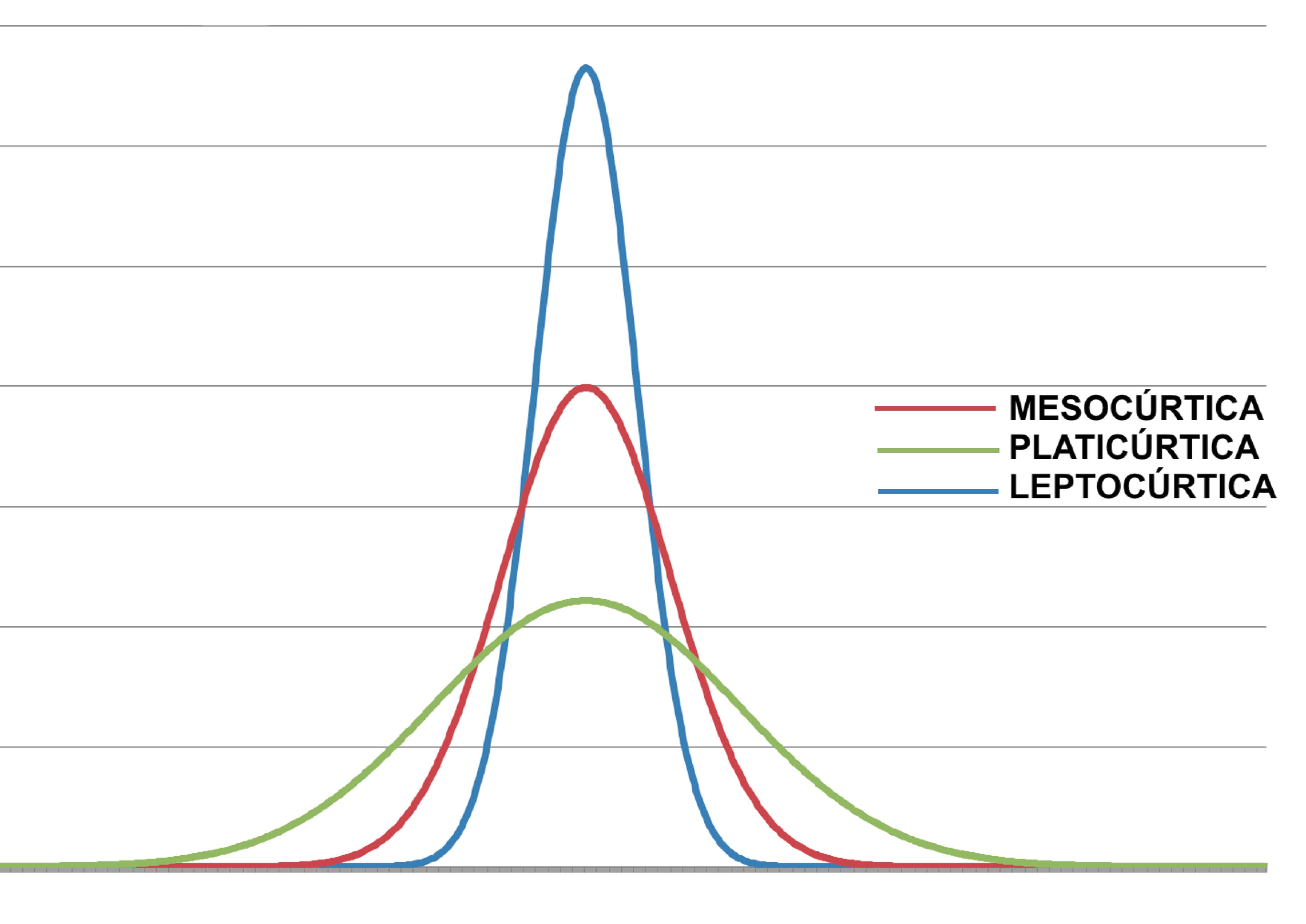
Figure 3.10: Diferentes aspectos de uma distribuição quanto à sua inclinação

Essas possíveis variações na forma de uma distribuição podem ser numericamente quantificadas através dos coeficientes de assimetria e curtose.

Uma das medidas do coeficiente de assimetria é através do primeiro ou segundo coeficientes de Pearson, dados pelas seguintes relações:

Primeiro coeficiente de assimetria de Pearson: $AS= \frac{ \stackrel{-}{x} - M_{o} }{ s }$
Segundo coeficiente de assimetria de Pearson: $AS = \frac{ 3 ( \stackrel{-}{x} - Q_{2}) } { s }$

Onde:

$\stackrel{-}{x}$ é a média;
$M_{o}$ é a moda;
$S$ é o desvio padrão; e,
$Q_{2}$ é o segundo quartil (mediana).

A assimetria é classificada do modo seguinte:

$-1 \leq AS \leq 1%=$ : distribuição simétrica;
$AS<-1$: distribuição com assimetria negativa; e,
$AS>1$: distribuição com assimetria positiva.

Uma das medidas do coeficiente de curtose é através da seguinte relação entre quartis e percentis:

\[ K = \frac{Q_{3} - Q_{1}} {2 \times(P_{90} - P_{10})} \]

Onde:

$Q_{3}$ = $3^{o}$ quartil;
$Q_{1}$ = $1^{o}$ quartil;
$P_{90}$ = $90^{o}$ percentil; e,
$P_{10}$ = $10^{o}$ percentil.

O coeficiente de curtose é classificado do modo seguinte:

k = 0,263: distribuição mesocúrtica;
k < 0,263: distribuição leptocúrtica; e,
k > 0,263: distribuição platicúrtica.

3.6 Diferentes posições da média, moda e mediana (2$^{o}$ quartil)

Essas três medidas podem se apresentar com valores em posições alternadas quando as comparamos:

quando a moda=mediana=média temos uma distribuição de frequências razoavelmente simétrica;
quando a moda $\leq$ mediana $\leq$ média (há uma quantidade maior de dados com grandes valores, arrastando a média para a direita, para cima) temos uma distribuição de frequências positivamente assimétrica, ; e,
quando a moda $\geq$ mediana $\geq$ média (há uma quantidade maior de dados com pequenos valores, arrastando a média para a esquerda, para baixo) temos uma distribuição de frequências negativamente assimétrica.

barplot(tab_alturas,
        main="Valores observados da alturas dos estudantes",
        xlab="Altura (cm)",
        ylab="Quantidade observada (un)",
        ylim=c(0,6),
        col="blue",
        las=0, 
        hor="FALSE")
abline(v=mean(19.9, 21.1), col="red")
text( mean(19.9, 21.1)-0.5, 5, "Média=1,69 m", col = "red", srt=90)
abline(v=median(18.7 , 19.9), col="darkgreen") 
text(median(18.7 , 19.9)-0.5, 5, "Mediana=1,675 m", col = "darkgreen", srt=90)
abline(v=c(16.3, 23.5), col="darkgrey") 
text(c(16.3-0.5, 23.5-0.5), 5, c("Moda=1,66","Moda=1,73"), col = "darkgray", srt=90)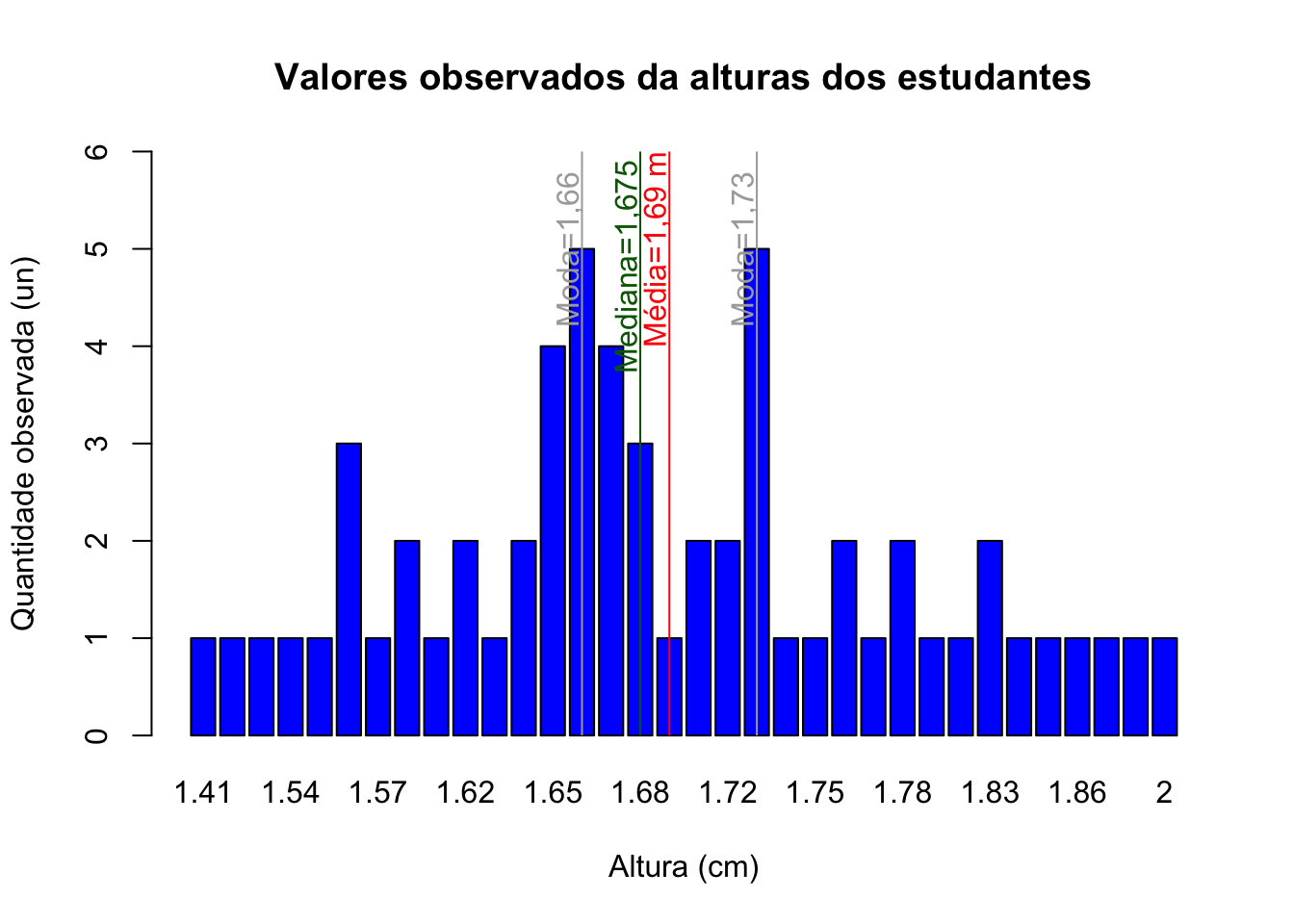

Figure 3.11: Valores observados das alturas dos estudantes e as posições da média, moda e mediana

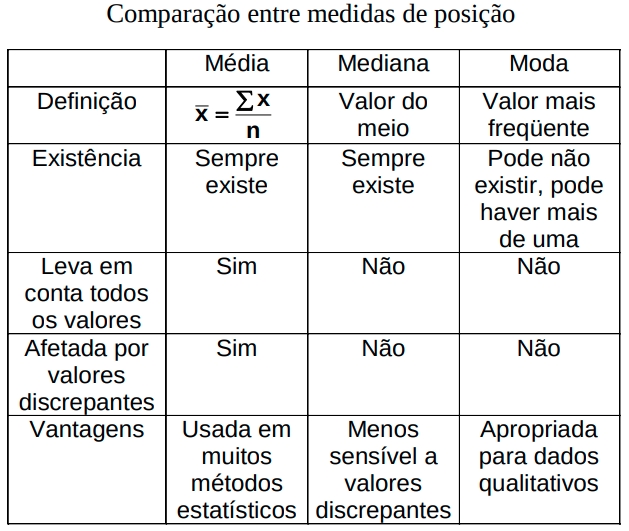
Figure 3.12: Quadro comparativo entre as medidas de tendência central (posição)

3.7 Apresentacao descritiva de dados na forma tabular

As sínteses numéricas expostas condensam ao máximo a informação trazida pelos dados na forma de estatísticas associadas à:

posição: média, moda, mediana;
dispersão: amplitude total dos dados, variância (esvio padrão), coeficiente de variação;
separatrizes (repartição): como por exemplo os quartis ($Q_{1}$; $Q_{2}$/mediana e $Q_{3}$).

A correta exposição dos dados na forma de tabelas e gráficos auxilia o entendimento de muitas outras características relacionadas aos dados trabalhados por parte do leitor com grande riqueza visual.

Ao se lidar com grandes conjuntos de dados a visualização da informação contida nos dados fica comprometida se eles forem simplesmente apresentados como uma listagem, mesmo que depurados de eventuais inconsistências e ordenados como a lista abaixo:

sort(alturas)

##  [1] 1.41 1.44 1.47 1.54 1.55 1.56 1.56 1.56 1.57 1.58 1.58 1.61 1.62 1.62 1.63
## [16] 1.64 1.64 1.65 1.65 1.65 1.65 1.66 1.66 1.66 1.66 1.66 1.67 1.67 1.67 1.67
## [31] 1.68 1.68 1.68 1.69 1.71 1.71 1.72 1.72 1.73 1.73 1.73 1.73 1.73 1.74 1.75
## [46] 1.76 1.76 1.77 1.78 1.78 1.79 1.82 1.83 1.83 1.84 1.85 1.86 1.93 1.95 2.00

Um dos modos de se lidar com isso é condensando a informação dos dados brutos em tabelas.

Uma tabela é uma forma não discursiva de apresentar informações nas quais o dado numérico se destaca como informação central. Uma tabela se diferencia de um quadro por este ter todos os seus campos delimitados por linhas e conter apenas informações de natureza qualitativa.

Uma tabela deve conter algumas informações essenciais, fora daquela estritamente relacionada aos dados, para que a compreensão do leitor acerca dos dados expostos seja a mais imediata possível:

título que explique o que a tabela contém, local, data;
cabeçalho nas colunas e linhas com a explicação, ainda que resumis, a que se referem as quantidades expostas no corpo;
corpo formado pelos dados referentes às variáveis;
fonte dos dados;
uniformidade no número de casas decimais apresentadas no corpo;
todas as casas devem apresentar valores ou símbolos que expliquem a ausência da informação (NI, NE, ou 0-zero).

Trabalhos de natureza acadêmica ou científica deveriam obrigatoriamente seguir, quando publicados no Brasil, a norma vigente publicada pela ABNT: Associação Brasileira de Normas Técnicas e algumas punlicações do IBGE: Instituto Brasileiro de Geografia e Estatística (como em link).

Observa-se frequentemente, todavia, que as publicações seguem normas particulares das instituições de ensino (para trabalhos de conclusão de curso, monografias, dissertações e teses) ou das editoras (artigos), muitas vezes mescladas com recomendações da ABNT. Na Universidade Estadual de Londrina o portal da biblioteca possui uma ligação para a seção “Normas para trabalhos” (link).

3.7.1 Apresentacao tabular de dados qualitativos

3.7.1.1 Dados qualitativos em entrada única

Para alguns tipos de dados, a apresentação tabular é bastante imediata.

Admita que tenha sido realizada uma pesquisa junto a um terminal de desembarque internacional em algum aeroporto sobre o continente de procedência do passageiro, num determinado período de um certo dia, tendo sido anotados os seguintes valores: AM, AM, A, A, A, AM, EU, EU, EU, EU, AM, AS, AS, AS, OC, AS, EU, AM, onde os continente anotados são assim identificados: americano (AM); africano (A), europeu (EU); asiático (AS) e da oceania (OC). Uma tabela para a apresentação dos resultados poderia ser:

Desembarques no terminal internacional A em Cumbica (SP, Brasil)
(10/10/2021: 8 h 00min às 12 h 00 min)
Continente de procedência	Desembarques
América	5
África	3
Europa	5
Ásia	4
Oceania	1
Total	18

Fonte: Próprio autor

Outro exemplo de apresentação tabular onde são apresentadas as proporções relativas observadas de cada nível da variável estudada (“tipo de família”, com quatro níveis diferentes), de um levantamento amostral feito pela Agência do Censo dos Estados Unidos em 2005.

Estrutura domiciliar dos Estados Unidos
Estrutura domiciliar	Número (milhões)	Freq. rel.	Freq. rel. (%)
Casal com filhos	24,1	0,22	22
Casal sem filhos	31,1	0,28	28
Solteiro, sem parceiro	19,1	0,17	17
Morando sozinho	30,1	0,27	27
Outros domicílios	6,7	0,06	6
Total	111.1	1,00	100%

Fonte: Censo dos EUA (2005)

3.7.1.2 Dados qualitativos em entrada dupla

Outros tipos de dados são provenientes de pesquisas que têm por base respostas de natureza binária como, por exemplo:

sim ou não;
gosto ou não gosto;
voto em “A” ou voto em “B”; ou,
concordo ou não concordo.

Como resultado final, são obtidas contagens que expressam as frequências absolutas observadas para cada uma das variáveis (ou seus níveis) como na apresentação tabular de dados qualitativos por Tabelas de Contingência.

As tabelas de contingência são usadas para associar duas ou mais variáveis qualitativas (ou seus níveis) às contagens das respostas obtidas, na forma das frequências absoluta e relativa observadas em cada uma dessas variáveis (ou seus níveis).

O uso desse tipo de tabela é comum quando se pretende investigar se as variáveis estudadas têm alguma associação por meio de testes não paramétricos. Esse tipo de apresentação facilita a extração de informações relacionadas às probabilidades marginais ou condicionadas de cada uma variáveis ou seus níveis.

Admita agora que a pesquisa anterior junto ao terminal de desembarque internacional tenha também apontado o sexo do passageiro em seu desembarque. Uma tabela de dupla entrada com aqueles dados assumiria a forma:

Desembarques no terminal internacional A em Cumbica (SP, Brasil)
(10/10/2021: 8 h 00min às 12 h 00 min)
Desembarques no terminal internacional A em Cumbica (SP, Brasil)	Sexo do passageiro		Total
	M	F	Total
América	3	2	5
África	3	0	3
Europa	1	4	5
Ásia	2	2	4
Oceania	0	1	1
Total	9	9	18

Fonte: Próprio autor

Um outro exemplo, usando dados da incidência de baixo peso ao nascer em recém-nascidos de Pelotas (RS) segundo o hábito tabágico da mãe durante a gravidez (1982):

Incidência de baixo peso ao nascer em recém-nascidos de Pelotas, RS, segundo o hábito tabágico da mãe durante a gravidez (1982)
Classificação da mãe	Baixo peso ao nascer		Total
Classificação da mãe	Sim	Não	Total
Fumante	275	2.144	2.419
Não fumante	311	4.496	4.807
Total	586	6.640	7.226

Fonte: Próprio autor

Ou ainda neste outro estudo que analisa a inclinação partidária de dois tipos de núcleos familiares em relação à presença de filhos:

Inclinação partidária (frequências absolutas)
Estrutura domiciliar	Democrata	Republicano	Totais
Casal com filho(s)	762	468	1230
Casal sem filhos	484	477	961
Totais	1246	945	2191

Fonte: Próprio autor

A partir das contagens obtidas na pesquisa (as frequências absolutas), uma tabela com as frequências relativas pode ser construída, passando a apresentar as proporções relativas de cada categoria em relação aos níveis pesquisados:

Inclinação partidária (frequências relativas)
Estrutura domiciliar	Democrata (%)	Republicano (%)	Totais (%)
Casal com filho(s)	34,78	21,36	56,14
Casal sem filhos	22,09	21,77	43,86
Totais (%)	56,87	43,13	100

Fonte: Próprio autor

3.7.2 Apresentacao tabular de dados quantitativos

Todavia, para grandes quatidades de observações de dados quantitativos, a apresentação na forma de tabelas deve ser precedida do agrupamento dos valores observados em classes. O procedimento estatístico de agrupar os dados em classes ou categorias envolve construir uma tabela de distribuição de frequências.

Uma tabela de distribuição de frequências associa cada classe (intervalo) de valores da variável estudada ao número de ocorrências observadas. Como regra prática, a repartição dos dados brutos em classes deve sempre observar para que não haja um número excessivo de classes (diminuição da finalidade de resumir os dados, criação de classes sem nenhuma observação) nem tampouco poucas (que não possibilitem a visualização da distribuição e promovam perda da informação original).

A construção de uma distribuição de frequências consiste essencialmente em:

escolher as classes ou intervalos (dados quantitativos) ou categorias (dados qualitativos);
separar ou enquadrar os dados nessas classes ou categorias; e,
contar o número de dados de cada classe ou categoria.

A literatura propõe vários modos para se determinar o número k de classes:

Crítério	Tamanho da amostra (n)	Fórmula
	n $\leq$ 25	k=5
Raiz quadrada	25 $\leq$ n $\leq$ 220	k=$\sqrt{n}$
Raiz quadrada	25 $\leq$ n $\leq$ 220	$2^{k} > n$
Herbert Sturges	135 $\leq$ 572237	k=1+3,22.log(n)$^{(1)}$
Giuseppe Milone	20 $\leq 36315$	k=-1+2.ln(n) $^{(2)}$

$^{(1)}$: logarítmo na base 10; e
$^{(2)}$: logarítmo na base e.

Ao se escolher um número ($k$) de classes deve-se ponderar para que:

os intervalos das classes tenham, geralmente, a mesma amplitude (raramente se necessita dispor de classes com amplitudes diferentes);
os intervalos, a faixa de variação que vai do limite inferior da primeira classe ao limite superior da **última classe*, devem conter todos os valores possíveis da variável;
cada valor observado deve pertencer apenas a uma classe;
nenhuma classe deverá estar vazia (sem observação alguma);
não adotar um número muito elevado de classes (de modo que cada classe possua poucas observações) e nem muito reduzido (de modo a esconder a variabilidade dos dados ao se reunir todas as observações em poucas faixas de valores);
alguns autores recomendam um número mínimo de 5 classes e um máximo de 15;
podemos considerar a amplitude de cada classe com uma casa decimal a mais que os dados de modo a facilitar a incorporação do último valor (mais elevado) na última classe.

Em nosso exemplo das alturas dos estudantes, a determinação do número de classes pelo critério da raiz quadrada ( n=60) sugere 8 classes (outros critérios: pelo menor inteiro tq. $2^{k}>n; k=6$, pelo critério de Sturges $k=6,86 \sim 7$, de Giuseppe Milone $k=8,18 \sim 9)$).

\[\begin{align*} k & =\sqrt{n} \\ & = 7,74 \\ \end{align*}\]

Arredondar para mais: $k=8$.

A amplitude total (A) dos valores observados é a simples diferença entre o valor máximo (2,00 m) e o valor mínimo (1,41 m):

\[\begin{align*} A & =2,00-1,41 \\ & =0,59 m \end{align*}\]

A amplitude de cada uma das classes ( $\Delta$) será dada pelo quociente da amplitude total ( A) pelo número de classes ( k).

\[\begin{align*} \Delta & = \frac{A}{k} \\ & = \frac{0,59}{8}\\ & = 0,07375 m \end{align*}\]

Arredondar para mais: $\Delta=0,075 m$.

As classes são então assim construídas:

Limite inferior da $1^{a}$ classe ($L_{inf_1}$): valor mínimo observado; e,
Limite superior da $1^{a}$ classe ($L_{sup_1}$): $L_{inf_1}$ + $\Delta$.

e assim sucessivamente atá a última classe.

Símbolos gráficos para intervalos:

Os símbolos abaixo indicam que o valor situado à sua esquerda está incluído no intervalo e o da direita não está:

\[ \vdash \\ {\bullet}-{\circ} \]

Os símbolos abaixo indicam que o valor situado à sua esquerda não está incluído no intervalo e o da direita **está incluído*:

\[ \dashv \\ {\circ}-{\bullet} \]

As tabelas que serão apresentadas a seguir estão sem os requisitos essenciais expostos anteriormente uma vez que o propósito é explicar a construção e cálculo dos valores de suas células.

Com $\Delta=0,075m$ as 8 classes ficam assim estabelecidas, tendo-se como ponto de partida o valor mínimo observado: 1,41 m - 1,485 m; 1,485 m - 1,56 m; 1,56 m - 1,635 m; 1,635 m - 1,71 m; 1,71 m - 1,785 m; 1,785 m - 1,86 m; 1,86 m - 1,935m; 1,935 - 2,01 m.

Ordenando-se os dados (para facilitar a identificação das observações) e atribuíndo cada elemento a uma única classe:

{ 1,41 ; 1,44 ; 1,47 ; 1,54 ; 1,55 ; 1,56 ; 1,56 ; 1,56; 1,57 ; 1,58 ; 1,58 ; 1,61 ; 1,62 ; 1,62 ; 1,63; 1,64 ;1,64 ; 1,65 ; 1,65 ; 1,65 ; 1,65 ; 1,66 ; 1,66 ; 1,66 ; 1,66 ; 1,66 ; 1,67 ; 1,67 ; 1,67 ; 1,67 ; 1,68 ; 1,68 ;1,68 ; 1,69 ; 1,71 ; 1,71 ; 1,72 ; 1,72 ; 1,73 ; 1,73 ; 1,73 ; 1,73 ; 1,73 ; 1,74 ; 1,75 ; 1,76 ; 1,76 ; 1,77 ; 1,78 ; 1,78; 1,79 1,82 ; 1,83 ; 1,83 ; 1,84 ; 1,85 ; 1,86 ; 1,93; 1,95 ; 2,00}

A tabela de distribuição de frequências com 8 classes, cada uma com amplitude 0,075 m, assume a forma:

Classe	Frequência absoluta ($f_{i}$)
1,41 m $\vdash$ 1,485 m	3
1,485 m $\vdash$ 1,56 m	2
1,56 m $\vdash$ 1,635 m	10
1,635 m $\vdash$ 1,71 m	19
1,71 m $\vdash$ 1,785 m	16
1,785 m $\vdash$ 1,86 m	6
1,86 m $\vdash$ 1,935 m	2
1,935m $\vdash$ 2,01 m	2
Total	60

Alternativamente, caso adotássemos como ponto de partida (um pouco abaixo do valor mínimo observado) o valor de 1,40 m e com amplitude de classe 0,08 m, uma tabela alternativa de distribuição de frequẽncias teria como classes : 1,40 m - 1,48 m; 1,48 m - 1,56 m; 1,56 m - 1,64 m; 1,64 m - 1,72 m; 1,72 m - 1,80 m; 1,80 m - 1,88 m; 1,88 m - 2,06 m.

Ordenando-se os dados (para facilitar a identificação das observações) e atribuíndo cada elemento a uma única classe:

{ 1,41 ; 1,44 ; 1,47 ; 1,54 ; 1,55 ; 1,56 ; 1,56 ; 1,56 ; 1,57 ; 1,58 ; 1,58 ; 1,61 ; 1,62 ; 1,62 ; 1,63 ; 1,64 ;1,64 ; 1,65 ; 1,65 ; 1,65 ; 1,65 ; 1,66 ; 1,66 ; 1,66 ; 1,66 ; 1,66 ; 1,67 ; 1,67 ; 1,67 ; 1,67 ; 1,68 ; 1,68 ;1,68 ; 1,69 ; 1,71 ; 1,71 ; 1,72 ; 1,72 ; 1,73 ; 1,73 ; 1,73 ; 1,73 ; 1,73 ; 1,74 ; 1,75 ; 1,76 ; 1,76 ; 1,77 ; 1,78 ; 1,78 ;1,79; 1,82 ; 1,83 ; 1,83 ; 1,84 ; 1,85 ; 1,86 ; 1,93 ; 1,95 ; 2,00; }

A tabela de distribuição de frequências com 7 classes, cada uma com amplitude 0,08 m, assume a forma:

Classe	Frequência absoluta ($f_{i}$)
1,40 m $\vdash$ 1,48 m	3
1,48 m $\vdash$ 1,56 m	2
1,56 m $\vdash$ 1,64 m	10
1,64 m $\vdash$ 1,72 m	21
1,72 m $\vdash$ 1,80 m	15
1,80 m $\vdash$ 1,88 m	6
1,88 m $\vdash$ 2,06 m	3
Total	60

Também podemos cogitar adotar alternativamente um intervalo de classe $\Delta=0,10$ m, com a primeira classe começando (um pouco abaixo do valor mínimo observado) na altura de 1,40 m; todavia, a última classe não iria contemplar o valor máximo observado (2,00 m) e necessitaíamos abrir mais uma classe apenas para incluí-lo.

Mas começando-se no valor mínimo obseravado (1,41 m) estaríamos assegurando que o limite superior da última classe incluiria o valor máximo observado (2,00 m). Assim, essas seriam as classes sob uma amplitude de 0,10 m: 1,41 m - 1,51 m; 1,51 m - 1,61 m; 1,61 m - 1,71 m; 1,71 m - 1,81 m; 1,81 m - 1,91 m; 1,91 m - 2,01 m. O total de 6 classes (1,41 m a 2,01 m) cobre toda faixa de variação dos valores dos dados (de 1,41 m a 2,00 m ) e é de rápida assimilação pelo leitor.

Ordenando-se os dados (para facilitar a identificação das observações) e atribuíndo cada elemento a uma única classe:

{1,41 ; 1,44 ; 1,47 ; 1,54 ; 1,55 ; 1,56 ; 1,56 ; 1,56 ; 1,57 ; 1,58 ; 1,58 ; 1,61 ; 1,62 ; 1,62 ; 1,63 ; 1,64 ;1,64 ; 1,65 ; 1,65 ; 1,65 ; 1,65 ; 1,66 ; 1,66 ; 1,66 ; 1,66 ; 1,66 ; 1,67 ; 1,67 ; 1,67 ; 1,67 ; 1,68 ; 1,68 ;1,68 ; 1,69 ; 1,71 ; 1,71 ; 1,72 ; 1,72 ; 1,73 ; 1,73 ; 1,73 ; 1,73 ; 1,73 ; 1,74 ; 1,75 ; 1,76 ; 1,76 ; 1,77 ; 1,78 ; 1,78 ; 1,79 ; 1,82 ; 1,83 ; 1,83 ; 1,84 ; 1,85 ; 1,86 ; 1,93 ; 1,95 ; 2,00}

A tabela de distribuição de frequências com 6 classes, cada uma com amplitude 0,10 m, assume a forma:

Classe	Frequência absoluta ($f_{i}$)
1,41 m $\vdash$ 1,51 m	3
1,51 m $\vdash$ 1,61 m	8
1,61 m $\vdash$ 1,71 m	23
1,71 m $\vdash$ 1,81 m	17
1,81 m $\vdash$ 1,91 m	6
1,91 m $\vdash$ 2,01 m	3
Total	60

Tabelas de distribuição de frequências mais completas podem montadas agregando muitas informações adicionais em novas colunas, mediante simples operações aritméticas.

Essas informações servem para tornar a visualização mais imediata e muitas delas são obtidas com operações matemáticas elementares:

Classe i: é a simples identificação de cada classe;
Amplitude ($\Delta_{i}$) da classe $i$: a diferença entre o valor do limite superior e o do inferior de cada classe;
Intervalo de valores da classe $i$ (onde seu limite inferior está contido e o limite superior não está contido);
Valor médio ($\stackrel{-}{x}_{i}$) de cada classe $i$: o valor de seu limite inferior mais a metade da amplitude da classe;
Frequência absoluta ($f_{i}$) da classe $i$: o número de observações contidas no intervalo da classe considerada;
Frequência relativa ($fr_{i}= \frac{f_{i}}{n}$) da classe $i$ (ou frequência relativa percentual, se assim apresentada): o quociente do número de observações $n_{i}$ contidas no intervalo da classe $f_{i}$, pelo número total de observações ($n$);
Frequência acumulada ($F_{i}$) da classe $i$ (ou frequência acumulada percentual, se assim apresentada): o número de observações com medidas contidas na classe $i$ e nas anteriores a ela;
Densidade absoluta ($\delta_{i}=\frac{f_{i}}{\Delta_{i}}$): o quociente do número de observações da classe ($f_{i}$) pela sua amplitude ($\Delta_{i}$);
Densidade relativa $\delta_{r_i}=\frac{fr_{i}}{\Delta_{i}}$: o quociente da frequência relativa ($fr_{i}$) pela amplitude ($\Delta_{i}$) da classe.

Vejo como exemplo as tabelas abaixo:

Classe	Int. de valores	Alt. média	Freq. abs.	Freq. rel.	Freq. rel. (%)	Freq. acumulada	Freq. acum. (%)
		($\stackrel{-}{x}_{i}$)	($f_{i}$)	($fr_{i}$)	($fr_{i\%}$)	($F_{i}$)	($F_{i\%}$)
1	1,41 $\vdash$ 1,51	1,46	3	0,05	5	3	5,00
2	1,51 $\vdash$ 1,61	1,56	8	0,13	13,33	11	18,33
3	1,61 $\vdash$ 1,71	1,66	23	0,38	38,33	34	56,66
4	1,71 $\vdash$ 1,81	1,76	17	0,28	28,34	51	85,00
5	1,81 $\vdash$ 1,91	1,86	6	0,10	10	57	95,00
6	1,91 $\vdash$ 2,01	1,96	3	0,05	5	60	100,00
Totais	-		60	1,00	100,00	-	-

Classe	Int. de valores	Freq. abs.	Amplitude	Dens. abs	Freq. rel.	Dens. rel.
		($f_{i}$)	($\Delta_{i}$)	($\delta_{i}$)	($fr_{i}$)	($\delta_{r_i}$)
1	1,41 $\vdash$ 1,51	3	0,10	30	0,05	0,5
2	1,51 $\vdash$ 1,61	8	0,10	80	0,13	1,33
3	1,61 $\vdash$ 1,71	23	0,10	230	0,39	3,83
4	1,71 $\vdash$ 1,81	17	0,10	170	0,28	2,83
5	1,81 $\vdash$ 1,91	6	0,10	60	0,10	1
6	1,91 $\vdash$ 2,01	3	0,10	30	0,05	0,5
Totais	-	60	-	-	1,00	-

3.7.3 Média

Nas tabelas de distribuições de frequências os resultados estão agrupados em intervalos de classes ($i$). Por essa razão, os dados perdem sua identidade individual e passam a se representados pelo valor médio de cada intervalo ($\stackrel{-}{x}_{i}$).

A média será então dada pelo produto deste valor médio de cada intervalo ($\stackrel{-}{x}_{i}$) pela frequência absoluta que ele apresentou (${n}_{i}$), dividido pela quantidade de dados ($n$).

Sejam $n_{1}, n_{2}, ..., n_{n}$ as frequências apresentadas para cada intervalo $i$ dos valores assumidos pela variável $X$ para o total $n$ de observações. Assim a média aritmética simples para dados agrupados será dada por:

\[ \stackrel{-}{x}=\frac{\sum _{i=1}^{k}{f}_{i}\cdot{\stackrel{-}{x}}_{i}}{n} \]

onde:

$\stackrel{-}{x}_{i}$: o valor médio do intervalo da classe $i$;
$f_{i}$: a frequência absoluta da classe $i$;
$k$ é o número de classes da tabela de distribuição de frequências;
$n$ é o número de dados da tabela (eventualmente, os dados podem se referir a toda a população sob estudo) .

3.7.4 Moda

Moda para dados apresentados na forma de uma distribuição de frequências:

\[ Mo = l_{inf} + (\frac{\Delta_{1}}{\Delta_{1} + \Delta_{2}}) \times \Delta_{i} \]

Primeiramente identificamos a(s) classe(s) modal(is): a(s) classe(s) com maior(es) frequência(s) absoluta $f_{i}$. Os demais elementos da expressão são:

$l_{inf}$: limite inferior da classe modal;
$\Delta_{1}$ frequência absoluta da classe modal menos a frequência absoluta da classe anterior à classe modal;
$\Delta_{2}$ frequência absoluta da classe modal menos a frequência absoluta da classe posterior à classe modal; e,
$\Delta_{i}$ é o intervalo da classe modal.

3.7.5 Mediana ($=Q_{2}=D_{5}=P_{50}$)

Mediana para dados apresentados na forma de uma distribuição de frequências:

\[ Md = l_{inf} + \left[ \frac{\frac{\sum_{i}^{k} f_{i}}{2} - F_{(md-1)}}{f_{md}} \right] \times \Delta_{i} \]

Primeiramente identificamos a classe mediana: a classe que contem o elemento de posição $\frac{n}{2}$ (basta observar a coluna da frequência absoluta acumulada: $F_{i}$, percorrendo-a até a classe $i$ que tenha valor $>\frac{n}{2}$. Os demais elementos da expressão da mediana são:

$l_{inf}$: limite inferior da classe mediana;
$F_{{(md-1)}}$: é a frequência absoluta acumulada até a classe anterior à classe mediana;
$f_{md}$: é a frequência absoluta da classe mediana; e,
$\Delta_{i}$: é o intervalo da classe mediana.

3.7.6 Variância

Variância para dados agrupados:

\[ S^{2}= \frac{1}{n-1} \times \left[ \sum _{i=1}^{k}{(\stackrel{-}{x}}_{i})^{2} \cdot {f}_{i} - \frac{{\left(\sum _{i=1}^{k}{\stackrel{-}{x}}_{i} \cdot {f}_{i}\right)}^{2} }{n}\right] \]

em que:

$\stackrel{-}{x}_{i}$: o valor médio do intervalo de cada classe $i$ ($lim_{sup_i}-lim_{inf_i}$);
$f_{i}$: a frequência absoluta de cada classe $i$;
$k$ é o número de classes da tabela de distribuição de frequências;
$n$ é o número de dados da tabela (eventualmente, os dados podem se referir a toda a população sob estudo) .

3.7.7 Quartis

Quartis para dados agrupados:

\[ Q_{i}= l_{inf_{Q_{i}}} + \Delta_{i} \frac{L_{Q_{i}} - f_{ac_{Q_{i-1}}}}{f_{Q_{i}}} \]

em que:

$n$ é o número de dados;
$Q_{i}$ é o quartil desejado: $i=1, 2, 3$;
$L_{Q_{i}}$ é posição do quartil desejado tal que:
- $L_{Q_{1}}=0.25n$
- $L_{Q_{2}}=0.5n$
- $L_{Q_{3}}=0.75n$
classe quartílica é a classe onde a posição do quartil desejado ( $L_{Q_{i}}$) se localiza;
$l_{inf_{Q_{i}}}$ é o limite inferior da classe quartílica;
$f_{{Q_{i-1}}}$ é a frequência acumulada da classe imediatamente anterior à classe quartílica;
$f_{Q_{i}}$ é a frequência absoluta de classe quartílica;
$\Delta_{i}$ é a amplitude da classe quartílica (frequentemente igual para todas).

3.8 Apresentacao descritiva de dados na forma grafica

Uma apresentação na forma gráfica torna ainda mais fácil a visualização das informações contidas nos dados. Há uma gama enorme de gráficos para a representação de dados a depender de sua natureza (qualitativa ou quantitativa).

3.8.1 Gráficos para uma variável qualitativa

ranking: barras;
parte em relação ao todo: setores;

3.8.1.1 Colunas

A partir das tabelas mostradas na seção 3.5.1.1 Dados qualitativos em entrada única, podemos elaborar a apresentação gráfica na forma de Gráficos de colunas:

desembarque=c('AM','AM','A','A','A','AM','EU','EU','EU','EU','AM','AS','AS','AS','OC','AS','EU','AM')
tab_desembarque=table(desembarque)

barplot(tab_desembarque,
        main="Desembarques no terminal internacional A em Cumbica \n(10/10/2021: 8 h 00min às 12 h 00 min)",
        sub= "Continente de procedência: América: AM; África: A; Europa: EU; Ásia: AS; Oceania: OC \nfonte: próprio autor",
        xlab="",
        ylab="Quantidade observada (un)",
        ylim=c(0,6),
        col="blue",
        las=0, 
        hor="FALSE")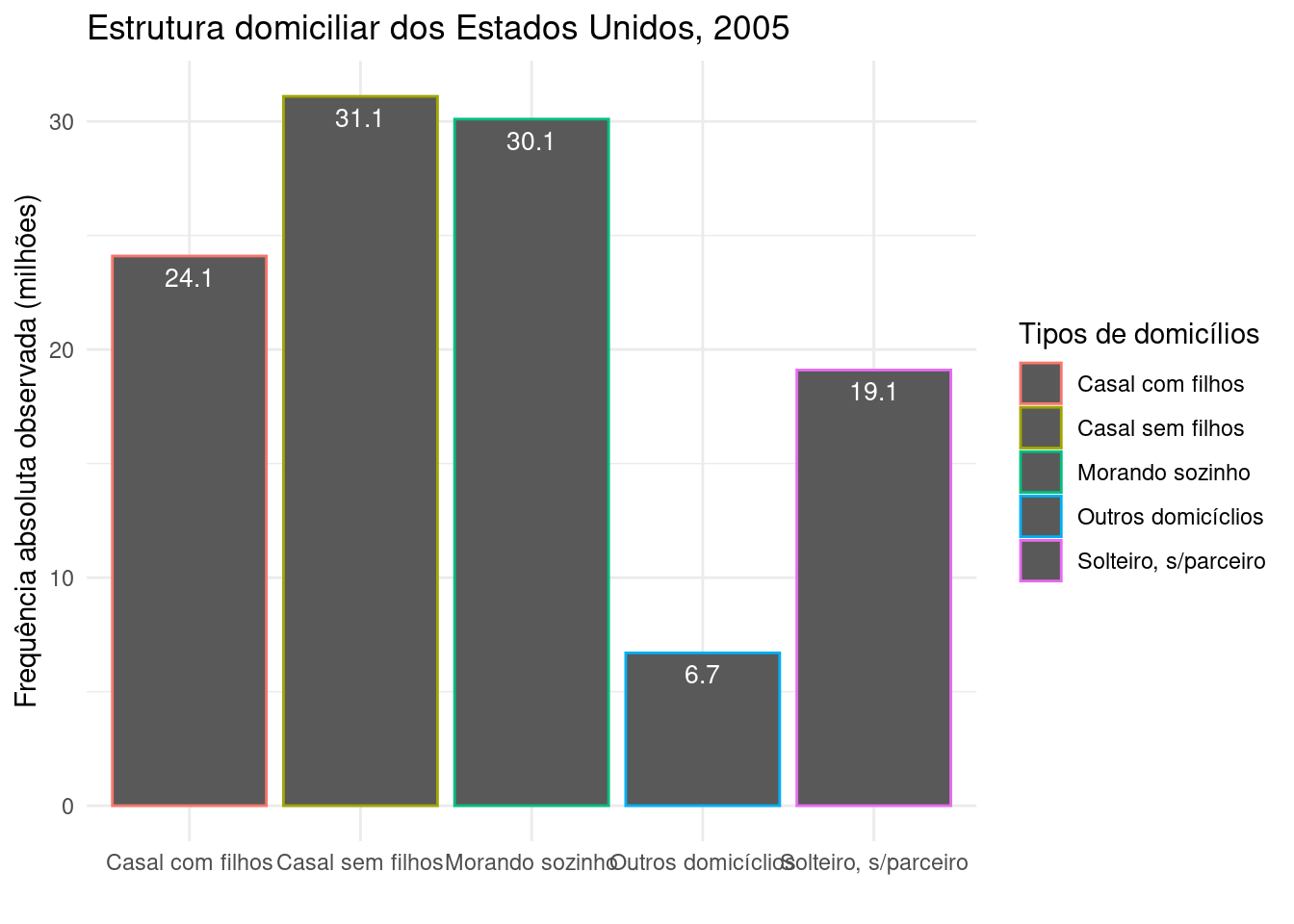

Figure 3.13: Gráfico de barras dos dados observados no terminal de desembarque internacional do aeroporto

library(ggplot2)
dados=data.frame(tipo=c("Casal com filhos",
                          "Casal sem filhos",
                          "Solteiro, s/parceiro",
                          "Morando sozinho",
                          "Outros domicíclios"),
                 quant=c(24.1, 31.1, 
                       19.1, 30.1,
                       6.7))

ggplot(dados, aes(x=tipo, y=quant, color=tipo)) +
geom_bar(stat="identity", position=position_dodge())+
ggtitle("Estrutura domiciliar dos Estados Unidos, 2005") +
theme(legend.position="bottom")+
geom_text(aes(label=quant), vjust=1.6, color="white", position = position_dodge(0.9), size=3.5)+
scale_fill_brewer(palette="Paired")+
theme_minimal()+
xlab("")  +
ylab("Frequência absoluta observada (milhões)")+
labs(colour = "Tipos de domicílios")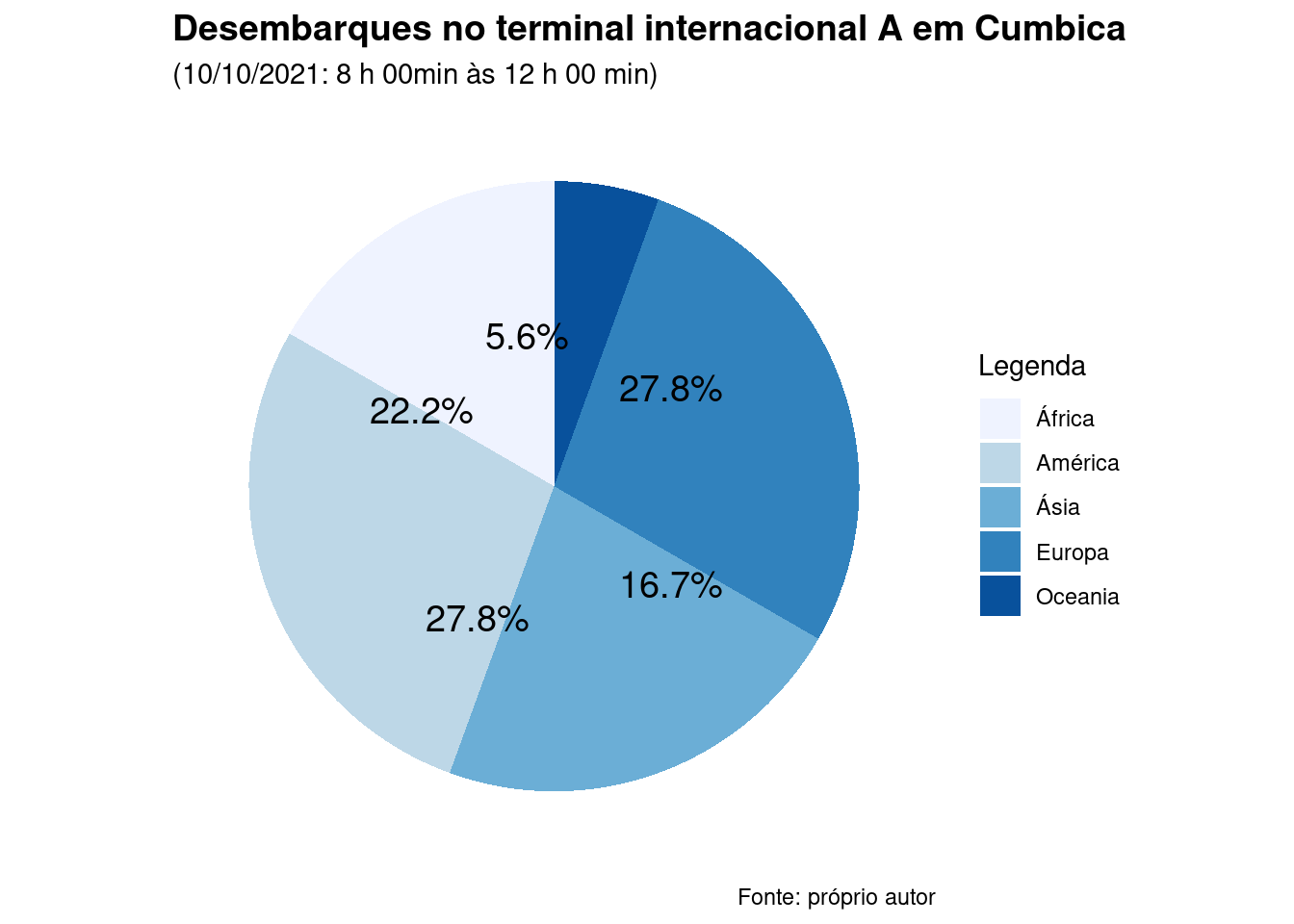

Figure 3.14: Gráfico de barras da estrutura domiciliar dos Estados Unidos

3.8.1.2 Setores

Em um Gráfico de setores a representação das quantidades está associada a uma fração do comprimento de um círculo. Para sua confecção considera-se a proporção da quantidade observada específica da quantidade total de dados, expressa na forma de fração do ângulo de um setor circular em relação ao ângulo interno total de um círculo (360^o).

library(scales)

## 
## Attaching package: 'scales'

## The following objects are masked from 'package:formattable':
## 
##     comma, percent, scientific

library(ggplot2)

desembarques_classes=data.frame(
  group = c("América","África","Europa","Ásia","Oceania"),
  value = c(5,3,5,4,1))


blank_theme=theme_minimal()+
  theme(
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    panel.border = element_blank(),
    panel.grid=element_blank(),
    axis.ticks = element_blank(),
    plot.title=element_text(size=14, face="bold")
  )

ggplot(desembarques_classes, aes(x="", y=value, fill=group)) +
  blank_theme +
  scale_fill_brewer("Blues")+
  labs(title="Desembarques no terminal internacional A em Cumbica", 
          subtitle="(10/10/2021: 8 h 00min às 12 h 00 min)",
           caption = "Fonte: próprio autor") +
  theme(axis.text.x=element_blank()) +
  geom_bar(width = 1, stat = "identity") +
  coord_polar("y", start=0) +
  geom_text(aes(y = value/2 + c(0, cumsum(value)[-length(value)]),
                label = percent(value/18 )), size=5)+
  guides(fill = guide_legend(title = "Legenda",
                             label.position = "right",
                             title.position = "top", title.vjust = 1))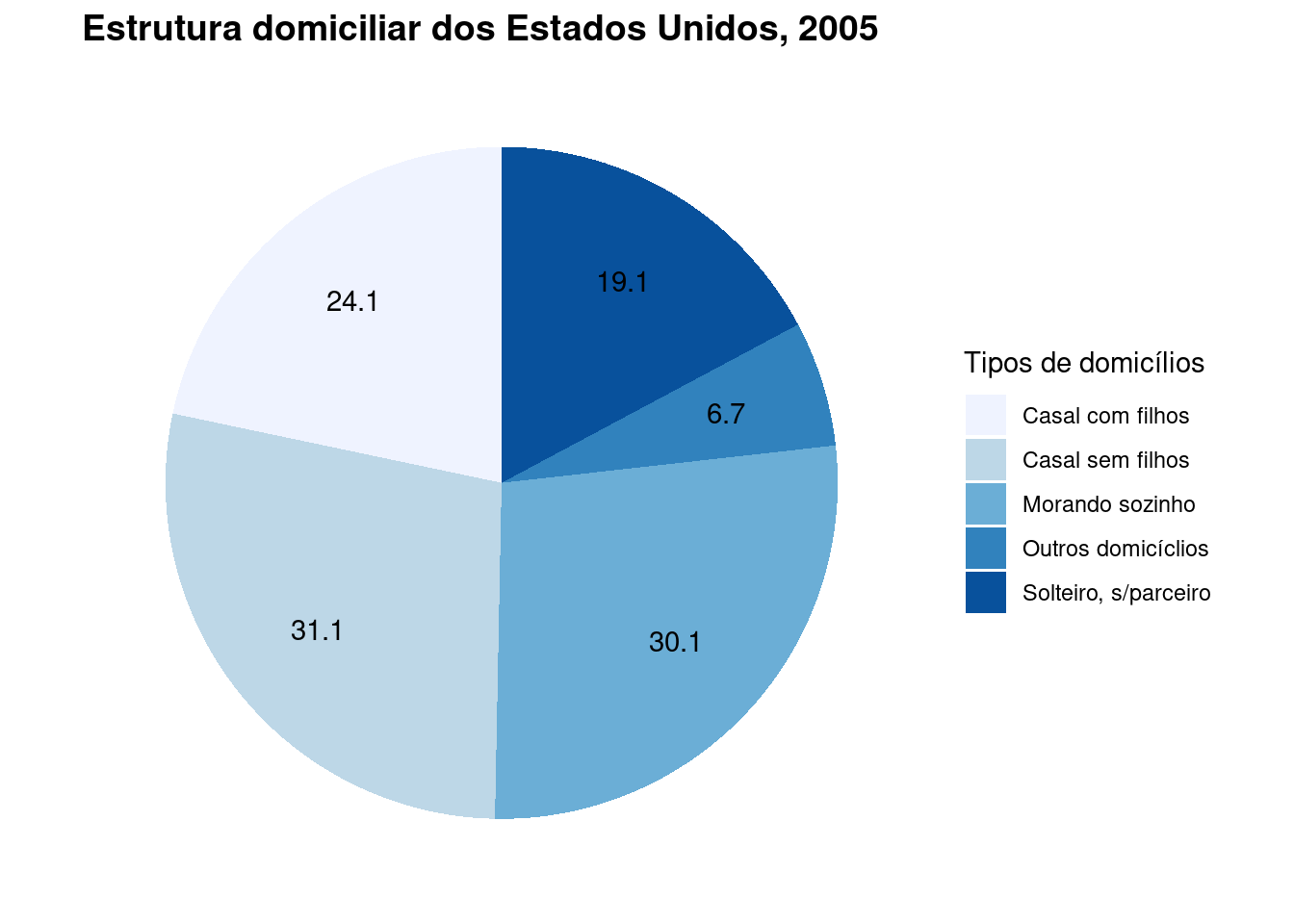

Figure 3.15: Gráfico de setores dos desembarques observados no terminal de desembarque internacional do aeroporto

library(ggplot2)
library(scales)

blank_theme=theme_minimal()+
  theme(
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    panel.border = element_blank(),
    panel.grid=element_blank(),
    axis.ticks = element_blank(),
    plot.title=element_text(size=14, face="bold")
  )

bp=ggplot(dados, aes(x="", y=quant, fill=tipo))+
  geom_bar(width = 1, stat = "identity")
pie=bp + coord_polar("y", start=0)
pie + 
  scale_fill_brewer("Blues")+
  blank_theme +
  theme(axis.text.x=element_blank()) +
  geom_text(aes(x =  1.2,label = quant), position = position_stack(vjust = 0.5)) +
  ggtitle("Estrutura domiciliar dos Estados Unidos, 2005") +
  theme(legend.position = "right", legend.justification = "center", legend.direction = "vertical",
        legend.spacing.x = unit(0.5, 'cm'),legend.spacing.y = unit(0.5, 'cm'))+
  guides(fill = guide_legend(title = "Tipos de domicílios",
                             label.position = "right",
                             title.position = "top", title.vjust = 1))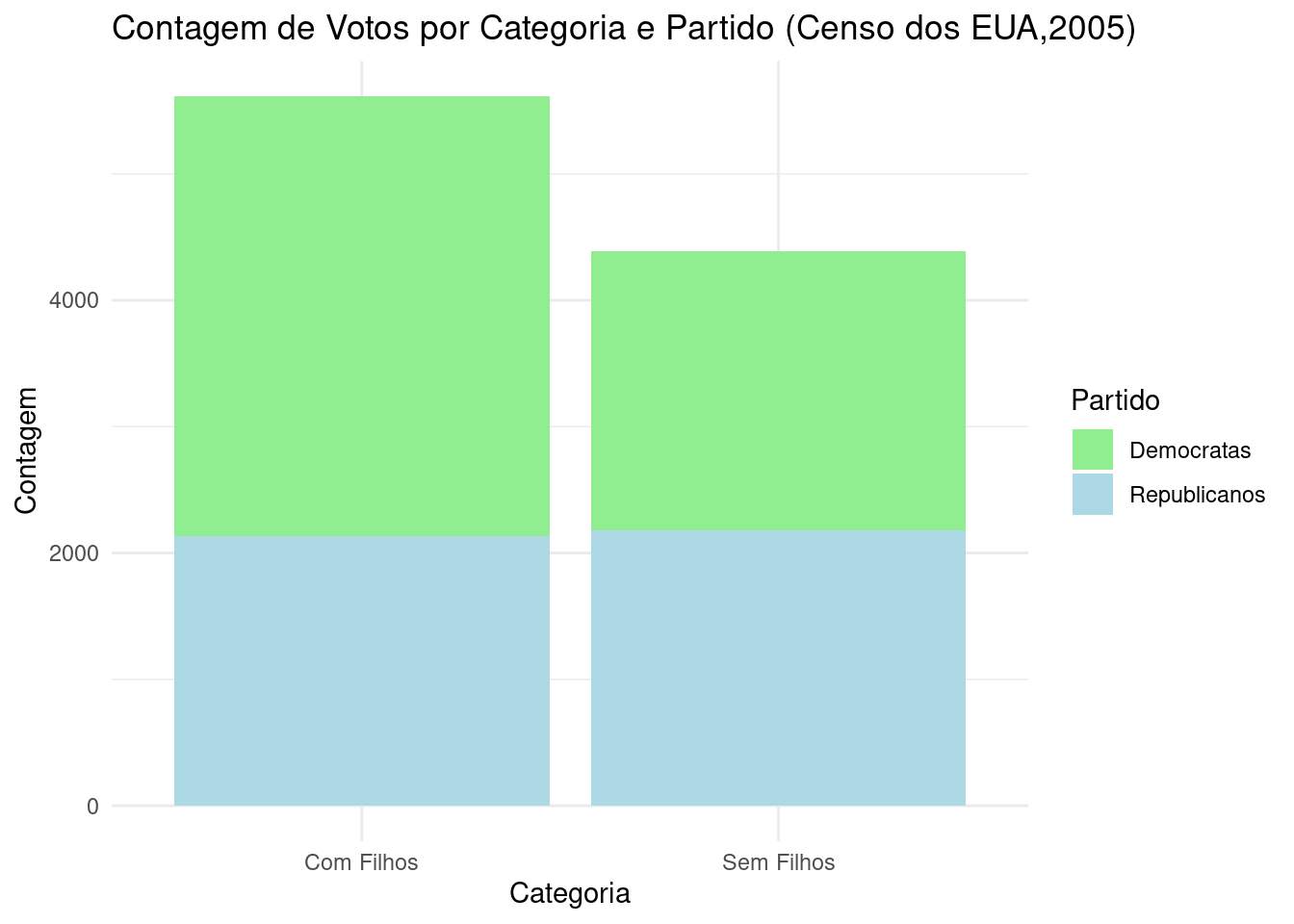

Figure 3.16: Gráfico de setores da estrutura domiciliar dos Estados Unidos

3.8.1.3 Colunas para dados em uma tabela de dupla entrada

library(ggplot2)             # Carrega a biblioteca ggplot2

# Dados fornecidos
casal_com_filho_democratas <- 3478
casal_com_filho_republicano <- 2136
casal_sem_filho_democratas <- 2209
casal_sem_filho_republicano <- 2177

# Criar um dataframe com os dados
dados <- data.frame(
  Categoria = c("Com Filhos", "Com Filhos", "Sem Filhos", "Sem Filhos"),
  Partido = c("Democratas", "Republicanos", "Democratas", "Republicanos"),
  Contagem = c(casal_com_filho_democratas, casal_com_filho_republicano,
               casal_sem_filho_democratas, casal_sem_filho_republicano)
)

# Criar o gráfico de barras empilhadas
ggplot(dados, aes(x = Categoria, y = Contagem, fill = Partido)) +
  geom_bar(stat = "identity") +
  labs(title = "Contagem de Votos por Categoria e Partido (Censo dos EUA,2005)",
       x = "Categoria",
       y = "Contagem") +
  scale_fill_manual(values = c("Democratas" = "lightgreen", "Republicanos" = "lightblue")) +
  theme_minimal()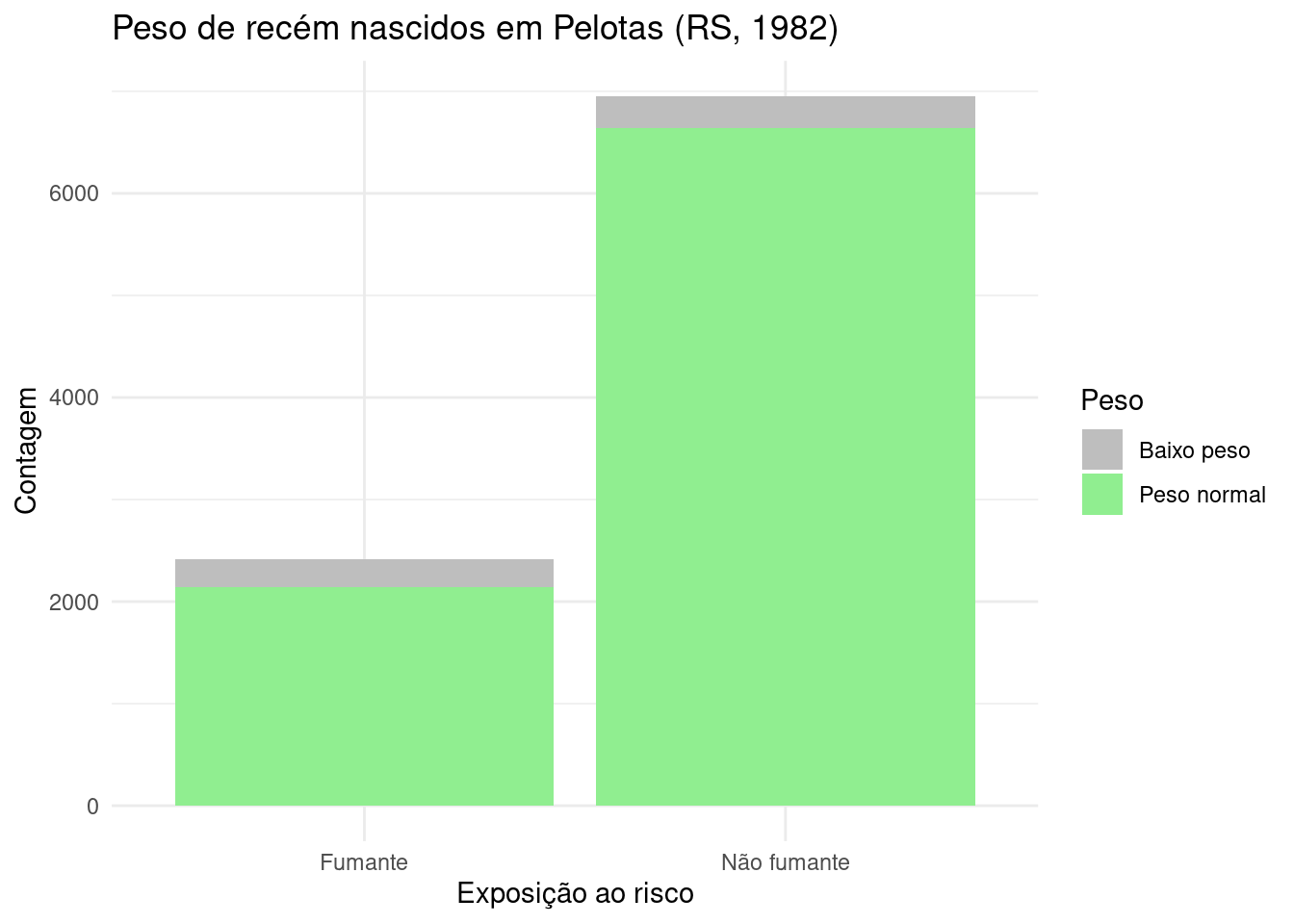

Figure 3.17: Gráfico de barras da estrutura familiar em relação à inclinação partidária nos Estados Unidos

library(ggplot2)             # Carrega a biblioteca ggplot2

# Dados fornecidos
fumantes_filho_bp = 275
fumantes_filho_pn = 2144
n_fumantes_filho_bp = 311
n_fumantes_filho_pn = 6640

# Criar um dataframe com os dados
dados <- data.frame(
  Risco = c("Fumante", "Fumante", "Não fumante", "Não fumante"),
  Peso = c("Baixo peso", "Peso normal", "Baixo peso", "Peso normal"),
  Contagem = c(fumantes_filho_bp, fumantes_filho_pn,
               n_fumantes_filho_bp, n_fumantes_filho_pn)
)

# Criar o gráfico de barras empilhadas
ggplot(dados, aes(x = Risco, y = Contagem, fill = Peso)) +
  geom_bar(stat = "identity") +
  labs(title = "Peso de recém nascidos em Pelotas (RS, 1982)",
       x = "Exposição ao risco",
       y = "Contagem") +
  scale_fill_manual(values = c("Baixo peso" = "gray", "Peso normal" = "lightgreen")) +
  theme_minimal()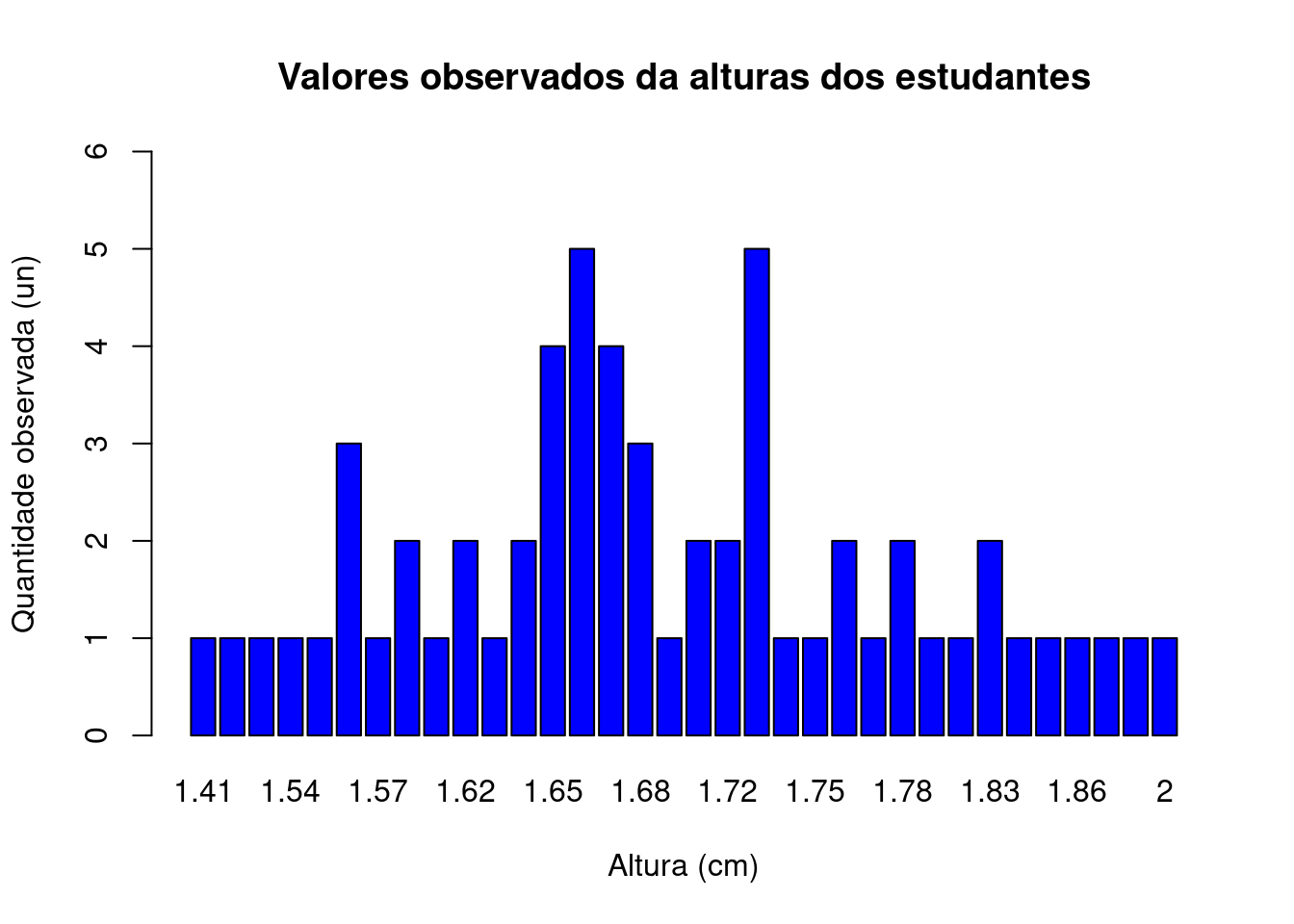

Figure 3.18: Gráfico de barras da exposição ao fator de risco e o efeito

3.8.2 Gráficos para uma variável quantitativa

diagrama de ramos e folhas;
dispersão unidimensional; e
barras;
histograma; e,
setores;
box plot.

3.8.2.1 Ramos e Folhas

Diagrama de Ramos e Folhas é uma apresentação híbrida pois ao mesmo tempo que espelha a quantidade de medidas observadas para cada altura, mantém as informações da listagem.

stem(alturas)

## 
##   The decimal point is 1 digit(s) to the left of the |
## 
##   14 | 147
##   15 | 45666788
##   16 | 12234455556666677778889
##   17 | 11223333345667889
##   18 | 233456
##   19 | 35
##   20 | 0

À esquerda do traço vertical (os ramos) são apresentadas frações das medidas das alturas (no caso, decímetros) e à direita (as folhas) são apresentadas os complementos dessas medidas (os centímetros) de tal modo que cada um dos dados da amostral original possa ter sua medida resgatada fazendo-se a leitura dos valores à esquerda com cada um deles à direita.

Essa apresentação também oferece uma apreciação visual a respeito de como os valores se distribuem.

3.8.2.2 Gráficos de dispersão unidimensional

Um Gráfico de dispersão unidimensional (stripchart) expressa visualmente duas informações: a localização de cada uma das medidas e a dispersão dos dados.

stripchart(alturas, method = "stack", offset=1,
           pch=20, at=0.5,
           main="Gráfico de dispersão unidimensional",
           col="blue",cex=1,
           xlab="Alturas dos estudantes (m)",
           ylab="Quantidades observadas (un)")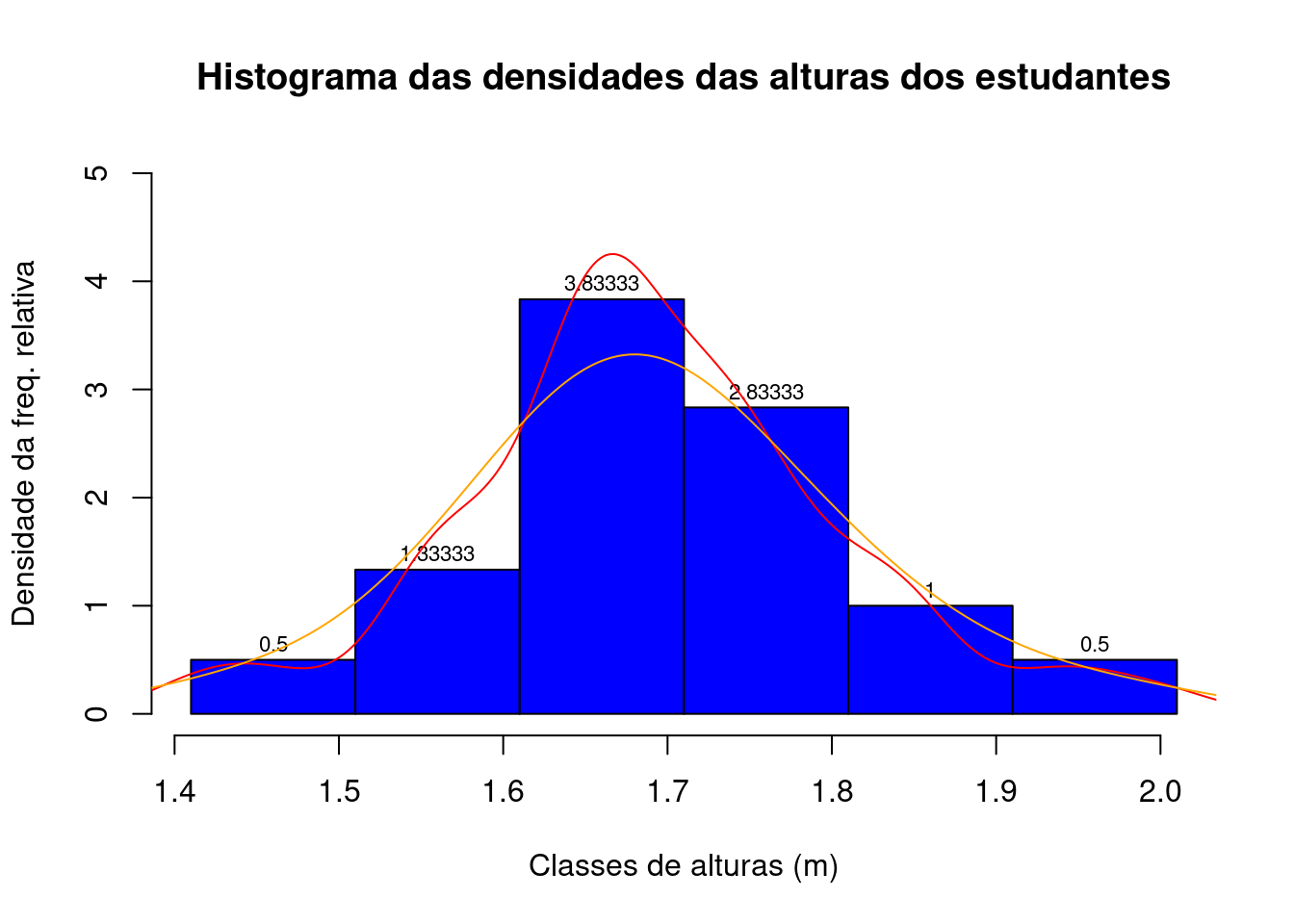

Figure 3.19: Gráfico de dispersão unidimensional (stripchart)

3.8.2.3 Barras

Se modificarmos o diagrama de ramos e folhas dos comprimentos e quantidades observadas, representando cada uma das alturas medidas por um retângulo cujas alturas sejam proporcionais à quantidade contada de cada uma dessas alturas teremos um Gráfico de barras.

tab_alturas=table(alturas)

barplot(tab_alturas,
        main="Valores observados da alturas dos estudantes",
        xlab="Altura (cm)",
        ylab="Quantidade observada (un)",
        ylim=c(0,6),
        col="blue",
        las=0, 
        hor="FALSE")

Figure 3.20: Gráfico de barras dos dados brutos: uma barra para cada observação e sua altura expressando o número de observações com esse valor

3.8.2.4 Histograma

Para dados quantitativos, o agrupamento dos valores brutos observados em classes (cada uma com um valor mínimo e máximo fixado) permite a geração de um Histograma, um tipo diferente de Gráfico de barras onde cada coluna está unida às colunas imediatamente adjacentes (indicando a continuidade de valores das medidas) e sua altura expressa a quantidade de observações contidas nessa classe.

Para as classes estabelecias na seção anterior o histograma das alturas dos estudantes terá esse aspecto:

h1=hist(alturas, breaks=seq(1.41 , 2.01 , 0.1),  include.lowest = TRUE, right = FALSE, main= "Histograma das alturas dos estudantes", col="blue", 
xlab="Classes de alturas (m)", ylab="Frequência absoluta observada (un)" , cex=0.7, ylim=c(0,30))
text(h1$mids,h1$counts,labels=h1$counts, adj=c(0.5, -0.5))
abline(v=mean(alturas), col="red") 
text(mean(alturas)-0.01, 28, "Média=1,69 m", col = "red", srt=90)
abline(v=median(alturas), col="darkgreen") 
text(median(alturas)-0.01, 27.2, "Mediana=1,675 m", col = "darkgreen", srt=90)
abline(v=Modes(alturas), col="darkgrey") 
text(Modes(alturas)+c(-0.01, -0.01), 27, c("Moda=1,66","Moda=1,73"), col = "darkgray", srt=90)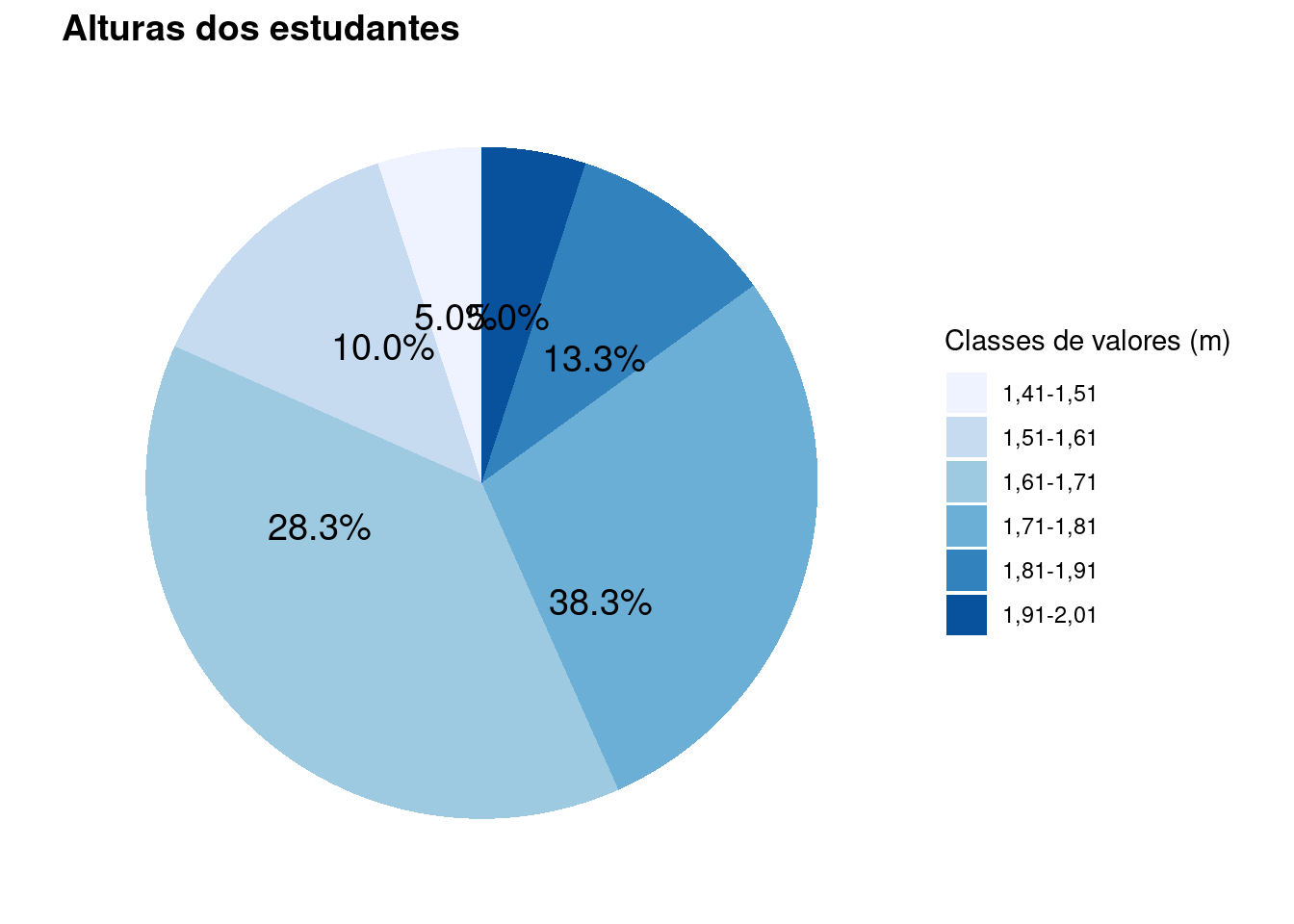

Figure 3.21: Histograma das alturas dos estudantes com as posições da média, moda e mediana

Um histograma é a representação gráfica de uma tabela de distribuição de frequências em colunas (retângulos).

A base de cada retângulo representa o intervalo de cada classe e a altura, a quantidade ou a frequência absoluta com que aquele valor da classe ocorre no conjunto de dados.

O termo histograma foi cunhado por Karl Pearson (c. 1891) e vem da composição em grego de istos (mastro) com gramma (escrita), convertida em inglês para historical diagram: histogram.

Como elemento gráfico, seu uso é anterior à sua denominação (maiores detalhes em: (link) ).

Num histograma de densidade, a altura de cada retângulo representa uma densidade relacionada à frequência relativa no intervalo de cada classe.

h2=hist(alturas,breaks=seq(1.41 , 2.01 , 0.10),  include.lowest = TRUE, right = FALSE, main= "Histograma das densidades das alturas dos estudantes", col="blue", 
xlab="Classes de alturas (m)", ylab="Densidade da freq. relativa", prob="TRUE", ylim=c(0,5))
text(h2$mids,h2$density,labels=round(h2$density, 5), adj=c(0.5, -0.5), cex=0.7)
lines(density(alturas), col="red")             
lines(density(alturas, adjust=2), col="orange")

A linha vermelha é uma aproximação da Função de Densidade da frequência relativa de observação (a linha preta é a curva da função densidade de uma distribuição Normal com média e variâncias dadas pelos dados

Figure 3.22: A linha vermelha é uma aproximação da Função de Densidade da frequência relativa de observação (a linha preta é a curva da função densidade de uma distribuição Normal com média e variâncias dadas pelos dados

Uma aproximação para a área sob a curva da Função de Densidade pode ser a soma das áreas das colunas, pois a área de cada retângulo é igual à proporção ($fr_{i}$) da classe ($i$) com:

Base = $\Delta_{i}$; e,
Altura =$\delta_{r_i}=\frac{fr_{i}}{\Delta_{i}}$.

cuja soma resultará em:

(0.10*0.5)+(0.10*1.333)+(0.10*3.833)+(0.10*2.833)+(0.10*1)+(0.10*0.50)

## [1] 0.9999

Alternativamente, determinadas as densidades relativas da cada classe, uma poligonal pode ser traçada e as áreas formadas por ela e a base desse gráfico podem ser igualmente determinadas a partir dos valores de $\Delta_{i}$ e $\delta_{r_i}$, cuja soma resultará aproximadamente 1.

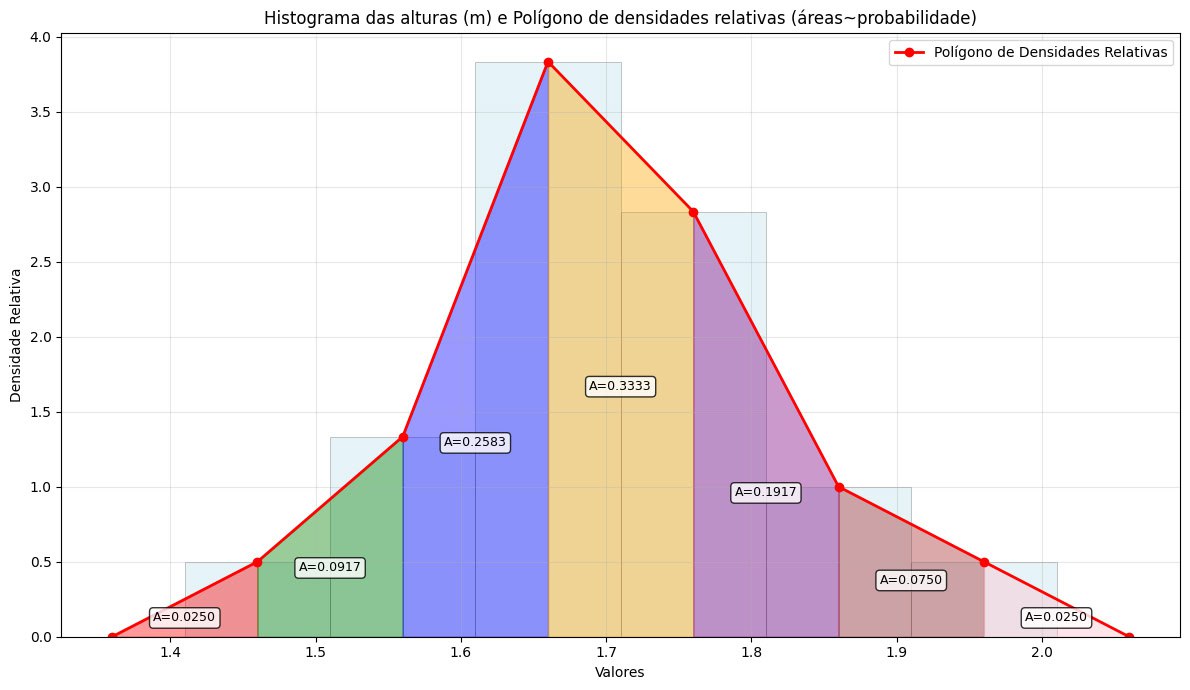
Figure 3.23: Polígono de densidades relativas como uma densidade empírica de probabilidade

A área da curva da Função de Densidade delimitada por dois valores quaisquer é uma analogia para a probabilidade de que um determinado valor de altura de um estudante (amostrado aleatoriamente dentre todos os 60 estudantes) esteja contida nesse intervalo.

Equivale dizer que, amostrando-se aleatoriamente um estudante dentre todos os 60 alunos, a probabilidade de que a altura desse estudante estaje contida entre os valores mínimo e máximo da amostra é, naturalmente, igual a 1 (100%)

3.8.2.5 Setores

library(scales)
library(ggplot2)

alturas_classes=data.frame(
  group = c("1,41-1,51",
            "1,51-1,61",
            "1,61-1,71",
            "1,71-1,81",
            "1,81-1,91",
            "1,91-2,01"),
  value = c(3,8,23,17,6,3))

blank_theme=theme_minimal()+
  theme(
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    panel.border = element_blank(),
    panel.grid=element_blank(),
    axis.ticks = element_blank(),
    plot.title=element_text(size=14, face="bold")
  )

ggplot(alturas_classes, aes(x="", y=value, fill=group)) +
  blank_theme +
  scale_fill_brewer("Blues")+
  ggtitle("Alturas dos estudantes") +
  theme(axis.text.x=element_blank()) +
  geom_bar(width = 1, stat = "identity") +
  coord_polar("y", start=0) +
  geom_text(aes(y = value/2 + c(0, cumsum(value)[-length(value)]),
                label = percent(value/60 )), size=5)+
  guides(fill = guide_legend("Classes de valores (m)",
                             label.position = "right",
                             title.position = "top", title.vjust = 1))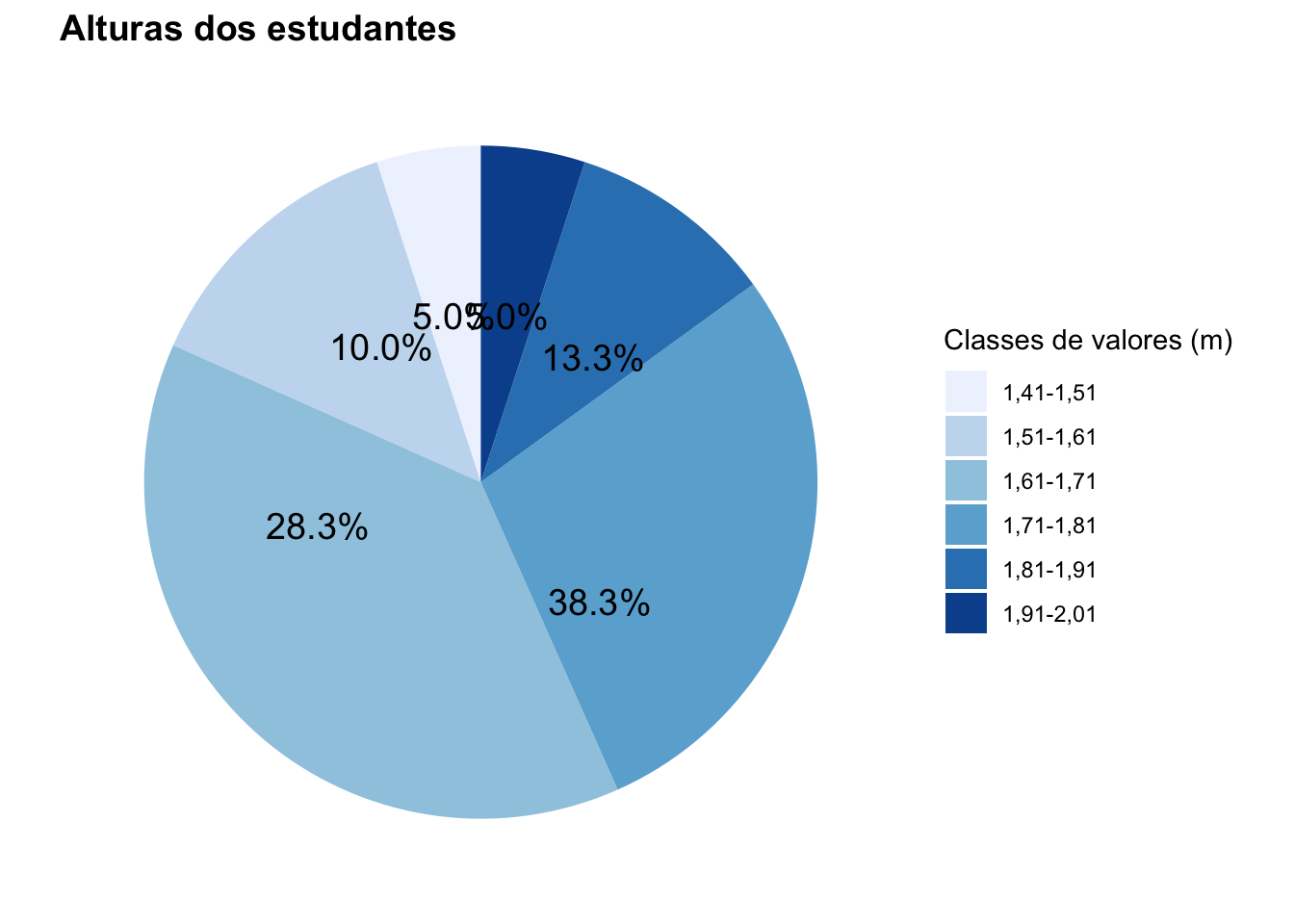

Figure 3.24: Gráfico de setores das alturas dos estudantes

3.8.2.6 Box-plot (gráfico de caixas)

O gráfico Box-plot ( box and whisker plot ): esse gráfico apresenta de modo conjunto, informações sobre a posição, dispersão, assimetria e dados discrepantes do conjunto analisado:

o segundo quartil (mediana): $Q_{2}$);
os valores mínimo: $x_{1}$ e máximo: $x_{n}$ (dados ordenados);
o 1$^{o}$ e 3$^{o}$ quartis;
a dispersão (intervalo interquartílico: $d_{q}=(Q_{3} - Q_{1})$);
um limite superior: $LS=Q_{3} + 1,50.d_{q}$;
um limite inferior: $LI=Q_{1} - 1,50.d_{q}$;
os valores mínimo e máximo observados (caso não existam valores superiores aos limites LI e LS); ou
as observações mais extremas, situadas fora dos limites LI e LS (são rotuladas como outliers).

Um outlier é uma observação que merece atenção do pesquisador. Pode tanto representar um dado realmente observado (pouco provável de sê-lo, mas que na pesquisa o foi), quanto um erro não amostral.

Roteiro para o Box-Plot cf. John Tukey ( Exploratory Data Analysis, 1977)

ordenar os valores (menor para o maior);
determinar os quartis;
calcular o intervalo (distância interquartílica);
calcular os limites superior e inferior;
traçar a caixa tendo por base os valores dos quartis;
traçar os limites inferior e superior;
analisar os valores dos dados pelo lado inferior (menores valores) e superior (maiores valores) e comparar com os limites
as hastes se estendem da caixa (primeiro quartil para baixo e terceiro quartil para cima) até a observação mais adjacente aos limites e que não os superam
as observações que superaram os limites ( outliers ) são identificadas com seus valores e permanecem no gráfico
remover o tracejado dos limites

min=min(alturas)
q1=1.635
q2=1.675
med=mean(alturas)
q3=1.755
max=max(alturas)
iq=q3-q1
ls=q3+1.5*iq
li=q1-1.5*iq
head(sort(alturas,TRUE)) #2.00 1.95 >>1.93<< 1.86 1.85 1.84

## [1] 2.00 1.95 1.93 1.86 1.85 1.84

tail(sort(alturas,TRUE)) # 1.56 1.55 1.54 1.47 1.44 >>1.41<<

## [1] 1.56 1.55 1.54 1.47 1.44 1.41

boxplot(alturas, 
        main="Boxplot do conjunto de dados de alturas",
        ylim=c(1.2, 2.1))

lines( y=c(1.47, 1.47), x=c(0.6,1), col="blue") 
text(x=0.60, y=1.47-0.05, "Delimitador inferior do bigode=1,47", col = "blue", srt=0)

lines( y=c(1.93,1.93), x=c(0.6,1), col="blue") 
text(x=0.60, y=1.93+0.05, "Delimitador superior do bigode=1,93", col = "blue", srt=0)

lines(y=c(med, med),  x=c(1,1.4), col="blue") 
text(x=1.4 , y= med+0.05 , "Média=1,6907", col = "blue", srt=0)

lines(y=c(q1, q1), x=c(1, 1.4), col="blue") 
text(x=1.4, y=q1 -0.05, "Primeiro quartil: Q1=1,635", col = "blue", srt=0)

lines(y=c(q2, q2),  x=c(0.6,1), col="blue") 
text(x=0.60 , y= q2 - 0.05, "Mediana: Q2=1,675", col = "blue", srt=0)

lines(y=c(q3, q3), x=c(1, 1.4), col="blue") 
text(x= 1.4 , y=q3 + 0.05, "Terceiro quartil: Q3=1,755", col = "blue", srt=0)

lines(y=c(li,li) , x=c(1.01,1.4) , col="red", lty=2) 
text(x=1.2, y=q1-1.5*iq-0.05 , "Limite inferior teórico: LI=1,455) ", col = "red", srt=0)

lines(y=c(ls,ls) , x=c(1.01,1.4) , col="red", lty=2) 
text(x=1.2, y=q3+1.5*iq +0.05 , "Limite superior teórico: LS=1,935", col = "red", srt=0)

points (y=1.47, x=1 , col="green", cex=1, lwd=5) 
text(x=1, y=1.47-0.05 , "Última observação dentro do LI: h=1,47 ", col = "green", srt=0)

points (y=1.93, x=1 , col="green", cex=1, lwd=5) 
text(x=1, y=1.93+0.05 , "Última observação dentro do LS: h=1,93 ", col = "green", srt=0)

Figure 3.25: Box-plot de um rol de valores com Distribuição Normal (média 20 e variãncia 5

Crítério	Tamanho da amostra (n)	Fórmula
	n \(\leq\) 25	k=5
Raiz quadrada	25 \(\leq\) n \(\leq\) 220	k=\(\sqrt{n}\)
Raiz quadrada	25 \(\leq\) n \(\leq\) 220	\(2^{k} > n\)
Herbert Sturges	135 \(\leq\) 572237	k=1+3,22.log(n)\(^{(1)}\)
Giuseppe Milone	20 \(\leq 36315\)	k=-1+2.ln(n) \(^{(2)}\)

Classe	Frequência absoluta (\(f_{i}\))
1,41 m \(\vdash\) 1,485 m	3
1,485 m \(\vdash\) 1,56 m	2
1,56 m \(\vdash\) 1,635 m	10
1,635 m \(\vdash\) 1,71 m	19
1,71 m \(\vdash\) 1,785 m	16
1,785 m \(\vdash\) 1,86 m	6
1,86 m \(\vdash\) 1,935 m	2
1,935m \(\vdash\) 2,01 m	2
Total	60

Classe	Frequência absoluta (\(f_{i}\))
1,40 m \(\vdash\) 1,48 m	3
1,48 m \(\vdash\) 1,56 m	2
1,56 m \(\vdash\) 1,64 m	10
1,64 m \(\vdash\) 1,72 m	21
1,72 m \(\vdash\) 1,80 m	15
1,80 m \(\vdash\) 1,88 m	6
1,88 m \(\vdash\) 2,06 m	3
Total	60

Classe	Frequência absoluta (\(f_{i}\))
1,41 m \(\vdash\) 1,51 m	3
1,51 m \(\vdash\) 1,61 m	8
1,61 m \(\vdash\) 1,71 m	23
1,71 m \(\vdash\) 1,81 m	17
1,81 m \(\vdash\) 1,91 m	6
1,91 m \(\vdash\) 2,01 m	3
Total	60

UNIVERSIDADE ESTADUAL DE LONDRINA
CCE - Centro de Ciências Exatas
DSTA - Departamento de Estatística (sala 11)
Prof. M.e Eng.\(^{o}\) Felinto Junior Da Costa
fjcosta@uel.br

Capítulo 3 Introdução à estatística descritiva

3.1 Análise exploratória

3.2 Dados brutos, em rol, diagrama de ramos & folhas e de dispersão unidimensional

3.3 Apresentacao descritiva de dados na forma de resumos numericos

3.3.1 Estimadores

3.3.2 Medidas de tendência central (posição)

3.3.2.1 Média

3.3.2.2 Moda

3.3.3 Medidas de dispersão (variabilidade)

3.3.3.1 Amplitude total dos dados

3.3.3.2 Variância (e desvio padrão)

3.3.3.3 Coeficiente de variação.

3.3.4 Medidas de subdivisão (separatrizes)

3.4 Padronizacao de dados (z-scores)

3.5 Medidas de forma (assimetria & curtose)

3.6 Diferentes posições da média, moda e mediana (2\(^{o}\) quartil)

3.7 Apresentacao descritiva de dados na forma tabular

3.7.1 Apresentacao tabular de dados qualitativos

3.7.1.1 Dados qualitativos em entrada única

3.7.1.2 Dados qualitativos em entrada dupla

3.7.2 Apresentacao tabular de dados quantitativos

3.7.3 Média

3.7.4 Moda

3.7.5 Mediana (\(=Q_{2}=D_{5}=P_{50}\))

3.7.6 Variância

3.7.7 Quartis

3.8 Apresentacao descritiva de dados na forma grafica

3.8.1 Gráficos para uma variável qualitativa

3.8.1.1 Colunas

3.8.1.2 Setores

3.8.1.3 Colunas para dados em uma tabela de dupla entrada

3.8.2 Gráficos para uma variável quantitativa

3.8.2.1 Ramos e Folhas

3.8.2.2 Gráficos de dispersão unidimensional

3.8.2.3 Barras

3.8.2.4 Histograma

3.8.2.5 Setores

3.8.2.6 Box-plot (gráfico de caixas)

Classe	Int. de valores	Alt. média	Freq. abs.	Freq. rel.	Freq. rel. (%)	Freq. acumulada	Freq. acum. (%)
		(\(\stackrel{-}{x}_{i}\))	(\(f_{i}\))	(\(fr_{i}\))	(\(fr_{i\%}\))	(\(F_{i}\))	(\(F_{i\%}\))
1	1,41 \(\vdash\) 1,51	1,46	3	0,05	5	3	5,00
2	1,51 \(\vdash\) 1,61	1,56	8	0,13	13,33	11	18,33
3	1,61 \(\vdash\) 1,71	1,66	23	0,38	38,33	34	56,66
4	1,71 \(\vdash\) 1,81	1,76	17	0,28	28,34	51	85,00
5	1,81 \(\vdash\) 1,91	1,86	6	0,10	10	57	95,00
6	1,91 \(\vdash\) 2,01	1,96	3	0,05	5	60	100,00
Totais	-		60	1,00	100,00	-	-

Classe	Int. de valores	Freq. abs.	Amplitude	Dens. abs	Freq. rel.	Dens. rel.
		(\(f_{i}\))	(\(\Delta_{i}\))	(\(\delta_{i}\))	(\(fr_{i}\))	(\(\delta_{r_i}\))
1	1,41 \(\vdash\) 1,51	3	0,10	30	0,05	0,5
2	1,51 \(\vdash\) 1,61	8	0,10	80	0,13	1,33
3	1,61 \(\vdash\) 1,71	23	0,10	230	0,39	3,83
4	1,71 \(\vdash\) 1,81	17	0,10	170	0,28	2,83
5	1,81 \(\vdash\) 1,91	6	0,10	60	0,10	1
6	1,91 \(\vdash\) 2,01	3	0,10	30	0,05	0,5
Totais	-	60	-	-	1,00	-