10.4 A aleatoriedade das proporções amostrais e o tamanho amostral

No módulo ``Introdução ao planejamento de pesquisas’’ explicamos que quando não se dispõe de nenhuma informação a priori sobre a proporção populacional (\(\pi\)) a adoção do máximo valor possível ao produto: \(\pi.(1-\pi)=\frac{1}{4}\) assegura que o o tamanho de amostra obtido será suficiente para a estimação qualquer que seja a proporção populacional \(\pi\). Trazendo a variável \(Z\) antes definida:

\[ Z=\frac{\hat{p}-\pi }{\sqrt{\frac{\pi \left(1-\pi \right)}{n}}} \sim N\left(0,1\right) \]

podemos reescrevê-la de modo a se obter o dimensionamento amostral em função do nível de confiança e um erro máximo estabelecidos:

\[ z_{(1-\alpha)}=\frac{\hat{p}-\pi }{\sqrt{\frac{\pi \left(1-\pi \right)}{n}}} \\ z_{(1-\alpha)}.\sqrt{\frac{\pi \left(1-\pi \right)}{n}}=\hat{p}-\pi \\ \frac{\pi \left(1-\pi \right)}{n}=(\frac{\varepsilon}{z_{(1-\alpha)}})^{2}\\ n = \frac{z_{(1-\alpha)}^{2}}{\varepsilon^{2}} \cdot \pi \left(1-\pi \right)\\ \]

Deste modo podemos simular a flutuação dos valores das proporções obtidas em sucessivas amostras, ilustrando simultaneamente as proporções amostrais observadas e a proporção das amostras que apresentam um erro amostral (\(\varepsilon\)) superior ao estipulado pelo nível de confiança (\(1-\alpha\)).

Desconhecendo-se qualquer informação acerca da proporção populacional (\(\pi\)), a dimensão da amostra pode ser estipulada tomando-se o maior valor do produto \(\pi \left(1-\pi \right)\) como sendo igual a \(\frac{1}{4}\) pois:

p <- seq(0, 1, by = 0.01)
y <- p * (1 - p)
plot(p, y, type = "l", xlab = "\u03c0", ylab = "\u03c0*(1- \u03c0)", main = "Possíveis valores assumidos pelo produto: \u03c0*(1- \u03c0)")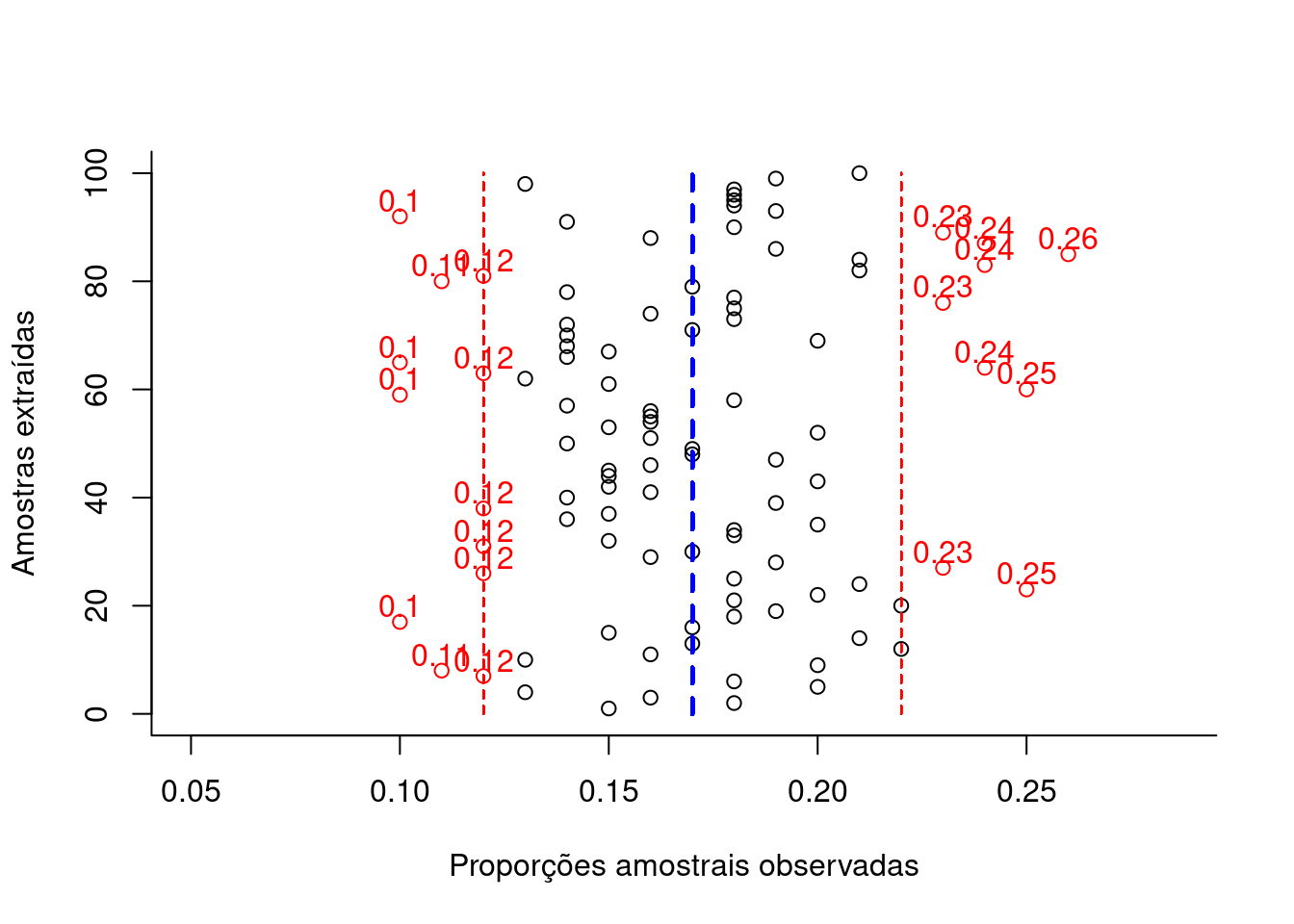

Figure 10.4: Possíveis valores assumidos pelo produto: π*(1- π)

Assim, a dimensão conservadora para a amostra será dada por:

\[ n = \frac{z_{(1-\alpha)}^{2}}{\varepsilon^{2}} \cdot \frac{1}{4}\\ \]

10.4.1 Simulações ilustrativas sobre as flutuações das proporções amostrais e o erro amostral fixado

As próximas figuras ilustram a flutuação das proporções amostrais obtidas de amostragens (com reposição) de elementos de uma população que apresentam a característica de interesse se manifestando de modo dicotômico, sob variados tamanhos amostrais (385, 210 e 100).

# Flutuação das proporções amostrais observadas

flut.N = function (N, n, p, conf, er) {
zc = qnorm(1-((1-conf)/2)) 
suc=rbinom(n=N, size = n, prob = p)
prop_suc=suc/n
dados=as.data.frame(prop_suc)
names=c("Proporção amostral")
colnames(dados)=names
row.names(dados)=NULL
meu_titulo01=paste0("Flutuação das proporções amostrais \n", N," amostras de tamanho ",n," (dimensionamento sob um nível de confiança (1-\u03b1)= ",conf," e um erro amostral \u03b5= ", er," \nAs linhas verticais mostram a propoção populacional em azul (\u03c0= ", p , ") \ne os valores limites estabelecidos pelo erro arbitrado em vermelho (\u03c0 +/-\u03b5= ",  p, "+/-", er ,")")   
meu_titulo02=paste0("Os valores das proporçoes amostrais seguem uma distribuição ~ N ( \u03bc, \u03c3) = (", round(mean(dados$`Proporção amostral`),4) ,", ", round(sqrt(p*(1-p)/n),4) ,")")


plot(0, 0, 
type="n", 
xlim=c( 0.5*min(dados$`Proporção amostral`) , 1.1*max(dados$`Proporção amostral`) ), 
ylim=c(0,N), 
bty="l",
xlab="Proporções amostrais observadas", 
ylab="Amostras extraídas", 
main="", #meu_titulo01  
sub="") #meu_titulo02

for (i in 1:N) {
prop_amostral=dados$`Proporção amostral`[i]
ploty = c(i,i)
if (prop_amostral > p+er || prop_amostral < p-er) 
     points(prop_amostral, i, col="red", cex=1)+text(y=i+3,x=prop_amostral, labels=round(prop_amostral,2), cex=1, col='red')
  else 
    points(prop_amostral, i, col="black", cex=1) 
segments(x0=p , y0=0, x1=p ,y1=N,col="blue", lwd=2, lty=2)
segments(x0=p-er , y0=0, x1=p-er ,y1=N,col="red", lwd=1, lty=2)
segments(x0=p+er , y0=0, x1=p+er ,y1=N,col="red", lwd=1, lty=2)
} 
}

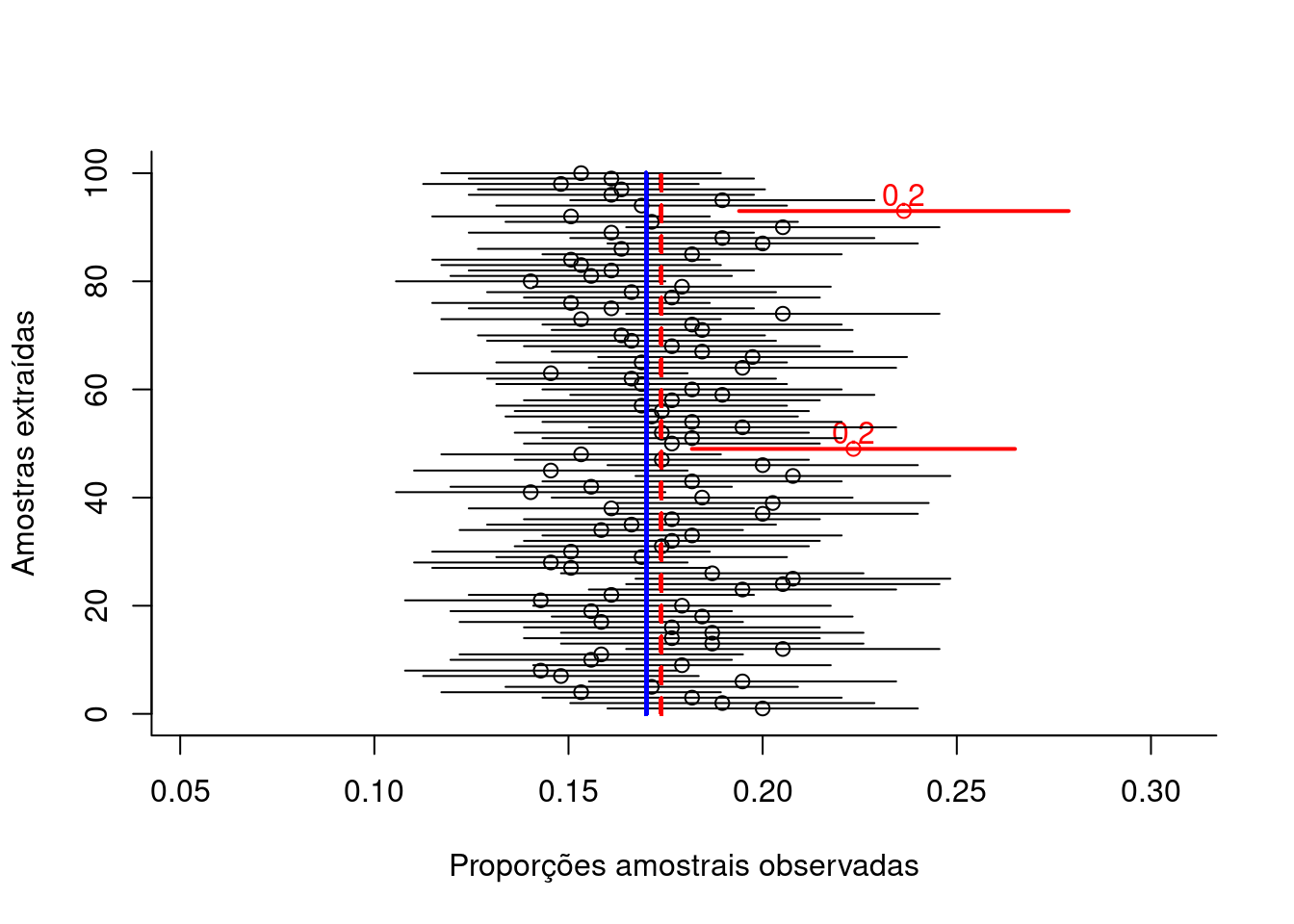
Figure 10.5: Flutuação das diversas proporções amostrais obtidas de amostragens cujo dimensionamento (385 elementos ) foi estimado ignorando-se o conhecimento da proporção populacional (π) para um nível de confiança (1-α)=0,95 e um erro amostral ε=0,05 (em preto as proporções amostrais dentro da tolerância fixada e, em vermelho, as que aleatoriamente ultrapassam a tolerância fixada em π +/-ε).

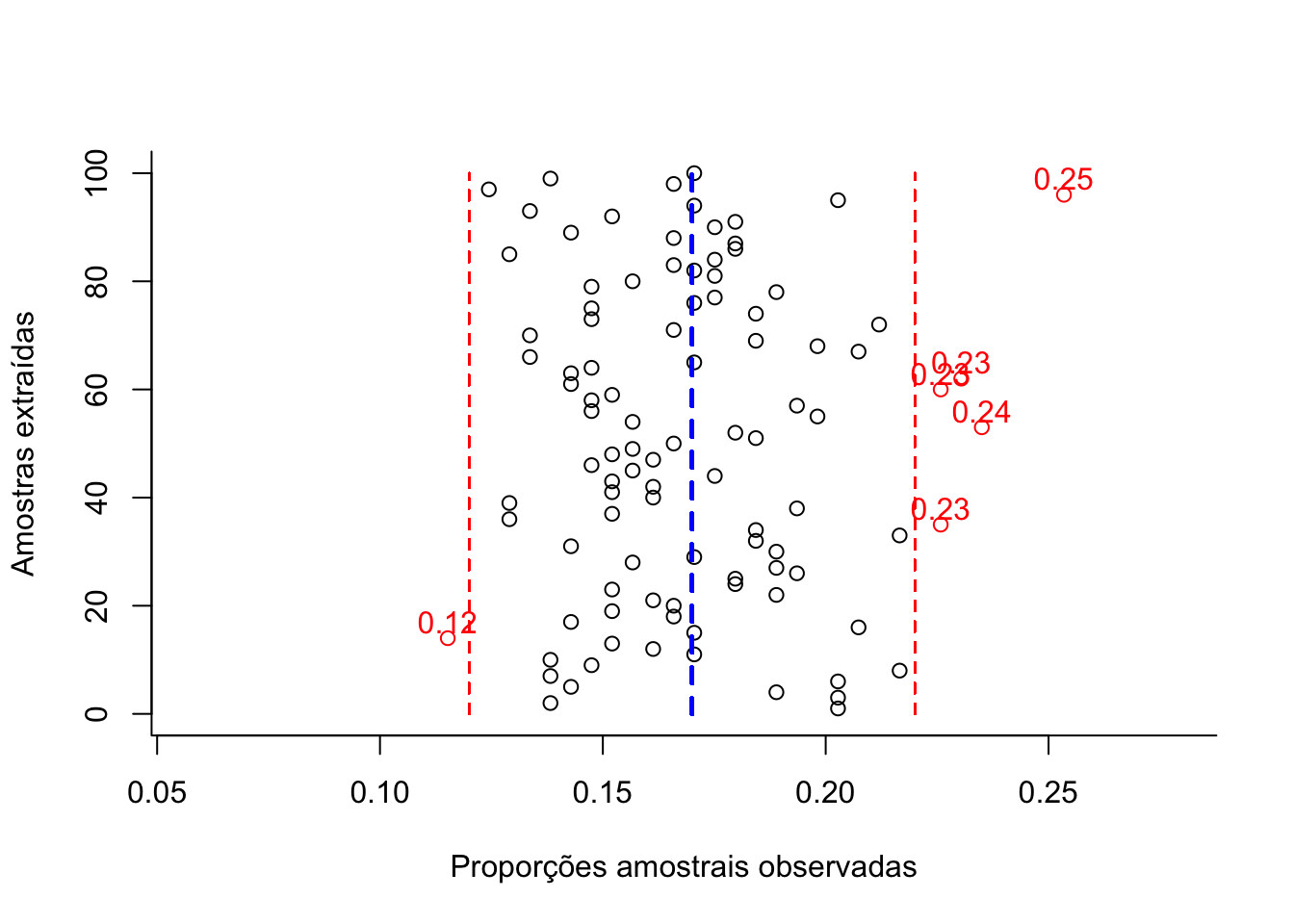
Figure 10.6: Flutuação das diversas proporções amostrais obtidas de amostragens cujo dimensionamento (217 elementos) foi estimado admitindo-se o conhecimento da proporção populacional (π) para um nível de confiança (1-α)=0,95 e um erro amostral ε=0,05 (em preto as proporções amostrais dentro da tolerância fixada e, em vermelho, as que aleatoriamente ultrapassam a tolerância fixada em π +/-ε).

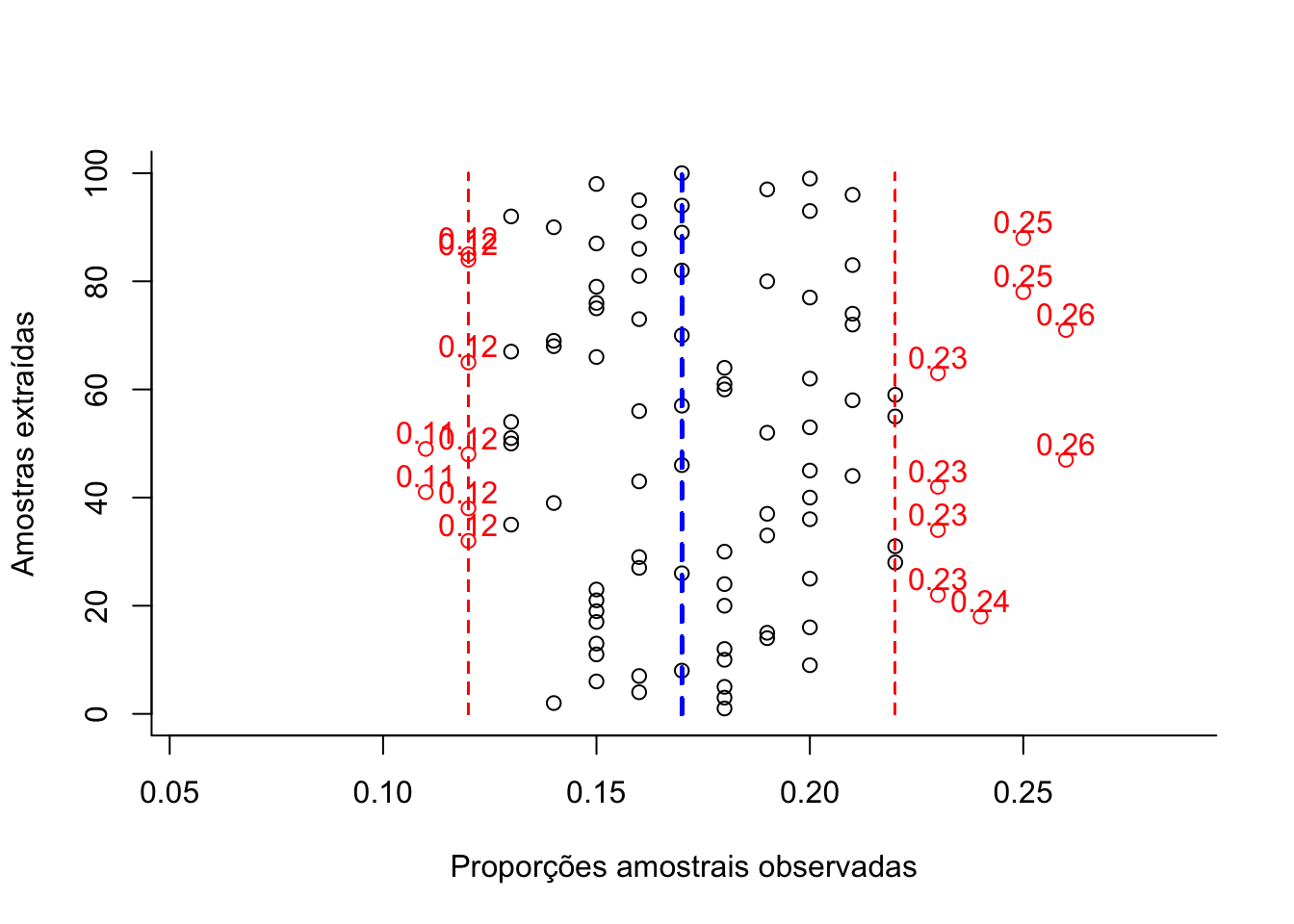
Figure 10.7: Flutuação das diversas proporções amostrais obtidas de amostragens cujo dimensionamento foi arbitrariamente fixado (100 elementos) para um nível de confiança (1-α)=0,95 e um erro amostral ε=0,05 (em preto as proporções amostrais dentro da tolerância fixada e, em vermelho, as que aleatoriamente ultrapassam a tolerância fixada em π +/-ε).