12.1 Contexto histórico

Sir Francis Galton (1822-1911), antropólogo e meteorologista inglês, propôs no artigo escrito em conjunto com J. D. Hamilton Dickson (Family Likeness in Stature) apresentado à Royal Society of London em 21 de janeiro de 1886, expressar por uma função uma relação que observou entre estaturas de pais e seus filhos e descendentes.
Nesse artigo, Galton verificou que, embora houvesse uma tendência de que pais mais altos tivessem filhos altos (e pais mais baixos, filhos mais baixos), a estatura média de crianças nascidas de pais com dada altura tendia a regredir à altura média da população como um todo. Nas palavras de Galton isso seria uma regressão à mediocridade: pais mais altos que a estatura média têm filhos mais baixos que eles
“Each peculiarity in a man is shared by his kinsman but, on the average, in a less degree[…]”
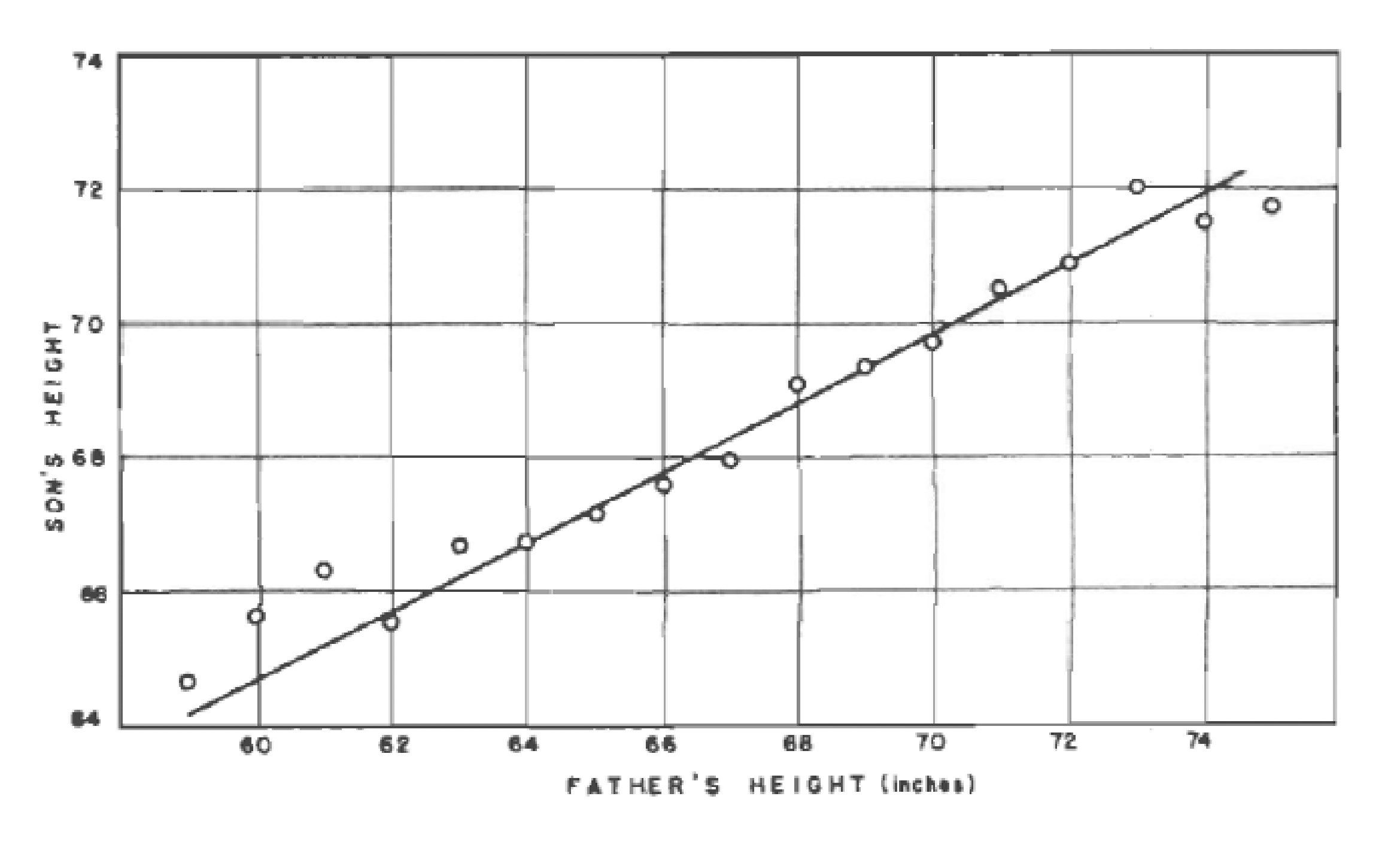
A Lei da Regressão de Galton foi referendada por Karl Pearson (On the Laws of Inheritance, 1903) poucos anos depois, quando analisou os dados de milhares de registros de estatura, tamanho do antebraço e da palma.
Em latim o prefixo co remete ao significado colaboração , união ou até simultaneidade. Correlação significa, portanto, uma relação mútua entre dois termos, uma correspondência.
Em Correlations and their Measurement, chiefly from Anthropometric Data, apresentado à Royal Society of London em dezembro de 1888, ele observou aquilo que viria a conceituar como co-relação ou correlação de estrutura.
Galton afirmou ao analisar o tamanho do braço com o da perna de um indivíduo que que dois órgãos são ditos serem correlacionados quando a variação de um é acompanhada, na média, pela variação para mais ou menos do outro:
- se a correlação fosse alta, uma pessoa com um braço longo teria também uma perna longa;
- se a correlação fosse moderada, o comprimento da perna não seria tão longo e,
- se não houvesse correlação, o comprimento de sua perna seria o comprimento médio desse membro na população.
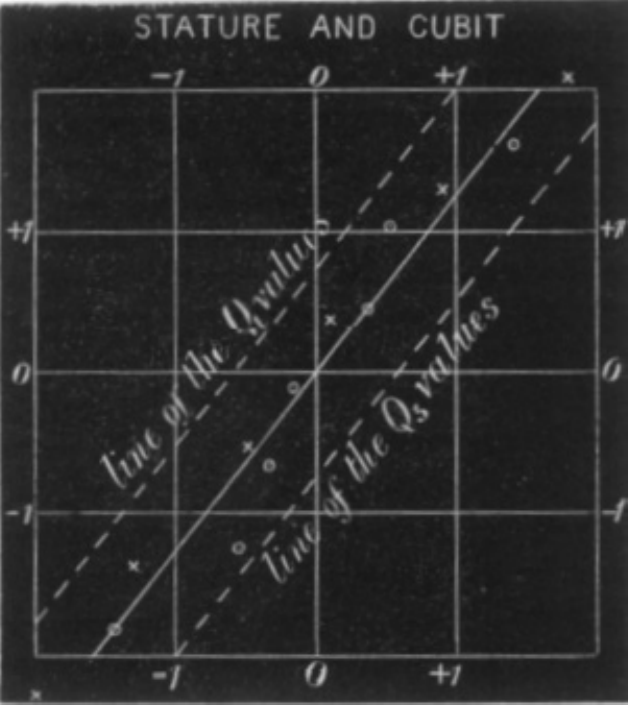
“…Assim, ele naturalmente atingiu uma linha de regressão reta com variabilidade constante para todas as matrizes de um caractere para um dado caractere de um segundo. Talvez fosse melhor para o progresso do cálculo correlacional que este simples caso especial fosse exposto primeiro: é tão facilmente compreendido pelo iniciante[…]”

Houve um momento que Johann Carl Friedrich Gauss considerou sua descoberta (1795) da regressão estatística como “trivial”. O método dos mínimos quadrados parecia tão óbvio para Carl Friedrich Gauss que ele imaginou não ter sido o primeiro a usá-lo. Ele não declarou publicamente sua descoberta até alguns anos depois ( Theoria motus corporum coelestium in sectionibus conicis solem ambientium, 1809), quando seu contemporâneo Adrien-Marie Legendre ( Nouvelles méthodes pour la détermination des orbites des comètes, 1805) publicou o método. Quando Gauss sugeriu que ele o havia usado antes deu-se partida a uma das mais famosas disputas de antecedência na história da ciência. Gauss acabaria recebendo a maior parte do crédito como fundador da regressão, mas não sem uma briga.