9.2 Intervalos de confiança
Um intervalo de confiança (\(IC\)) pode ser entendido com a faixa de valores delimitada por um mínimo e um máximo, calculados como função direta de um nível de confiança e da variabilidade e inversa da tamanho amostral.
\[ \text{estimativa amostral} \pm confiança.\sqrt\frac{variabilidade}{n} \]
Raramente se dispõe de informação a respeito da variabilidade (\(\sigma^{2}\)) da população estudada. Assim, a variabilidade populacional será frequentemente incorporado na expressão acima, com ligeiras modificações, na forma de sua estimativa amostral (\(S^{2}\)).
De certo modo, um intervalo de confiança reflete uma estimativa objetiva da (im)precisão e do tamanho da amostra de determinada pesquisa e, assim, podemos considerá-lo como uma medida da qualidade da amostra e da pesquisa.
O nível de confiança é designado pela quantidade \((1-\alpha)\) na qual \(\alpha\) é denominado de nível de significância, uma medida da probabilidade de erro.
Dependendo do nível de confiança que escolhemos os limites superior e inferior do intervalo mudam para uma mesma estimativa amostral. Os intervalos de confiança mais utilizados na literatura são os de 90%, 95%, 99% e menos de 99,9%.
O intervalo de confiança de 95% é tradicionalmente o intervalo mais utilizado na literatura e isso está relacionado ao nível de significância estatística (\(P<0,05\)) geralmente mais aceito.
Quanto menor for a amplitude de um intervalo, maior será a precisão da estimativa. Todavia, somente estudos com amostras razoavelmente grandes resultarão em um intervalo de confiança estreito, indicando simultaneamentente com alta precisão e alto grau de confianla a estimativa do parâmetro.
Intervalos de confiança podem ser construídos a quase todas as quantidades estatísticas e suas diferenças (quando se procura estudar se há ou não diferenças entre os parâmetros de duas populaçoes) como, por exemplo:
- médias;
- proporções; e,
- variâncias.
Um intervalo de confiança estabelecido sob certa probabilidade não deve ser interpretado como sendo a faixa de valores, delimitada por um mínimo e máximo, entre os quais o parâmetro da população (o qual se estima ou sobre o qual se infere) se insere.
Mas sim que, extraíndo-se um grande número de amostras de igual tamanho e da mesma população, e construindo-se para cada uma dessas amostras um intervalo de confiança de um mesmo nível de significância (\(\alpha\)), observaremos que uma determinada proporção desses intervalos, chamada de nível de confiança (\(1-\alpha\)) irá, de fato, conter o parâmetro sobre o qual se estima ou sobre o qual se infere. Por conseguinte, uma proporção desses intervalos chamada de nível de significância (\(\alpha\)) não irá conter o verdadeiro valor do parâmetro populacional.
Assim, \((1-\alpha)\) traduz o grau de confiança que se tem que um intervalo de confiança, calculado sobre uma estatística advinda de uma particular amostra de tamanho \(n\) da variável aleatória \(X\), inclua o verdadeiro valor do parâmetro da população:
IC.N = function (N, n, mu, sigma, conf) {
dados=data.frame()
plot(0, 0,
type="n",
xlim=c(mu-0.4*mu,mu+0.4*mu),
ylim=c(0,N),
bty="l",
xlab="Escala de valores da variável",
ylab="Intervalos amostrais construídos",
main=paste0("Intervalos com iguais níveis de confiança fixados em ", 100*conf, "% \n(",N," amostras de tamanho ",n,")") ,
sub=paste0("Parâmetros da distribuição da população Normal ( \u03bc, \u03c3) = (",mu,", ", sigma,")"))
abline(v=mu, col='red', lwd=2, lty=2)
#axis(1, at = c(mu-1*mu, mu, mu+1*mu))
zc = qnorm(1-((1-conf)/2))
#sigma.xbarra = sigma/sqrt(n)
for (i in 1:N) {
x = rnorm(n, mu, sigma)
media = mean(x)
erro= media-mu
sd = sd(x)
li = media - zc * sd/(sqrt(n))
ls = media + zc * sd/(sqrt(n))
temp=cbind(mu, media, erro, li, ls)
dados=rbind(dados, temp)
plotx = c(li,ls)
ploty = c(i,i)
if (li > mu | ls < mu) lines(plotx,ploty, col="red", lwd=2, lend=0)
else lines(plotx,ploty, lend=0)
if (li > mu | ls < mu) points(media, i, col="red", cex=1)+text(y=i+3,x=media, labels=round(media,1), cex=1, col='red')
else points(media, i, col="black", cex=1)
}
colnames(dados)=c("mu", "media", "erro", "li", "ls")
return(dados)
}
## mu media erro li ls
## 1 9.421 9.306 -0.115482 8.397 10.214
## 2 9.421 9.440 0.018528 8.482 10.397
## 3 9.421 10.269 0.848258 9.336 11.202
## 4 9.421 9.592 0.170963 8.521 10.663
## 5 9.421 9.216 -0.205314 8.390 10.042
## 6 9.421 9.339 -0.082497 8.299 10.378
## 7 9.421 9.488 0.066721 8.354 10.622
## 8 9.421 9.796 0.374945 8.832 10.760
## 9 9.421 9.698 0.276784 8.644 10.751
## 10 9.421 9.226 -0.194658 8.280 10.173
## 11 9.421 9.466 0.044820 8.292 10.639
## 12 9.421 9.294 -0.127016 8.290 10.298
## 13 9.421 8.485 -0.936184 7.410 9.560
## 14 9.421 9.643 0.222152 8.482 10.804
## 15 9.421 9.043 -0.377630 8.081 10.005
## 16 9.421 8.615 -0.805604 7.724 9.507
## 17 9.421 8.994 -0.426640 8.038 9.951
## 18 9.421 9.796 0.375491 8.614 10.979
## 19 9.421 9.405 -0.016151 8.380 10.429
## 20 9.421 9.273 -0.147927 8.258 10.288
## 21 9.421 9.415 -0.005602 8.378 10.453
## 22 9.421 10.644 1.223441 9.645 11.644
## 23 9.421 9.532 0.111373 8.466 10.599
## 24 9.421 9.767 0.346391 8.818 10.716
## 25 9.421 9.389 -0.032318 8.233 10.544
## 26 9.421 9.440 0.019190 8.292 10.589
## 27 9.421 10.308 0.886625 9.255 11.361
## 28 9.421 9.781 0.360236 8.756 10.806
## 29 9.421 8.334 -1.086862 7.277 9.391
## 30 9.421 10.207 0.785654 9.103 11.310
## 31 9.421 9.509 0.088400 8.618 10.401
## 32 9.421 9.463 0.042001 8.318 10.608
## 33 9.421 8.357 -1.063607 7.296 9.418
## 34 9.421 9.666 0.245322 8.454 10.879
## 35 9.421 9.794 0.372599 8.729 10.858
## 36 9.421 10.378 0.957009 9.456 11.300
## 37 9.421 9.815 0.394352 8.828 10.803
## 38 9.421 8.718 -0.702531 7.773 9.664
## 39 9.421 9.385 -0.036470 8.385 10.384
## 40 9.421 9.198 -0.223468 8.128 10.267
## 41 9.421 9.798 0.377167 8.878 10.718
## 42 9.421 10.452 1.031037 9.364 11.540
## 43 9.421 9.271 -0.149725 8.276 10.266
## 44 9.421 8.865 -0.556286 7.760 9.970
## 45 9.421 9.937 0.515732 8.984 10.889
## 46 9.421 10.296 0.875422 9.346 11.247
## 47 9.421 10.022 0.601456 9.169 10.876
## 48 9.421 10.125 0.704221 9.243 11.007
## 49 9.421 8.864 -0.556548 7.790 9.939
## 50 9.421 9.907 0.485984 8.924 10.890
## 51 9.421 8.601 -0.820189 7.631 9.571
## 52 9.421 8.877 -0.543852 7.882 9.872
## 53 9.421 8.868 -0.552976 7.885 9.851
## 54 9.421 9.587 0.165913 8.861 10.313
## 55 9.421 9.120 -0.301051 8.094 10.146
## 56 9.421 8.264 -1.156911 7.119 9.409
## 57 9.421 10.365 0.943503 9.478 11.251
## 58 9.421 9.704 0.283043 8.576 10.832
## 59 9.421 8.819 -0.602045 7.785 9.853
## 60 9.421 10.081 0.660230 9.100 11.062
## 61 9.421 9.182 -0.238955 8.055 10.310
## 62 9.421 10.050 0.629488 9.065 11.036
## 63 9.421 8.709 -0.711512 7.634 9.785
## 64 9.421 10.362 0.940970 9.304 11.420
## 65 9.421 10.031 0.609546 9.132 10.929
## 66 9.421 9.209 -0.212332 8.253 10.164
## 67 9.421 9.360 -0.060828 8.380 10.341
## 68 9.421 9.640 0.218875 8.669 10.611
## 69 9.421 10.075 0.653853 8.970 11.180
## 70 9.421 9.106 -0.315456 8.062 10.149
## 71 9.421 9.209 -0.211971 8.220 10.198
## 72 9.421 9.056 -0.365493 7.969 10.142
## 73 9.421 8.929 -0.492221 7.875 9.983
## 74 9.421 9.693 0.271661 8.791 10.595
## 75 9.421 8.701 -0.720118 7.702 9.699
## 76 9.421 10.060 0.638863 9.116 11.003
## 77 9.421 9.301 -0.120325 8.271 10.331
## 78 9.421 8.868 -0.553380 7.767 9.968
## 79 9.421 9.696 0.275151 8.607 10.785
## 80 9.421 9.778 0.357038 8.743 10.813
## 81 9.421 9.036 -0.384507 8.019 10.054
## 82 9.421 9.737 0.315514 8.908 10.565
## 83 9.421 8.249 -1.172126 7.281 9.216
## 84 9.421 9.121 -0.300296 8.058 10.183
## 85 9.421 10.544 1.123322 9.496 11.593
## 86 9.421 9.254 -0.166649 8.370 10.139
## 87 9.421 10.583 1.161816 9.603 11.562
## 88 9.421 8.706 -0.715343 7.734 9.678
## 89 9.421 10.224 0.803220 9.318 11.130
## 90 9.421 8.561 -0.859514 7.637 9.486
## 91 9.421 9.827 0.406058 8.864 10.790
## 92 9.421 9.317 -0.104483 8.058 10.575
## 93 9.421 9.812 0.391441 8.870 10.755
## 94 9.421 9.134 -0.287109 8.146 10.122
## 95 9.421 9.286 -0.134997 8.406 10.166
## 96 9.421 9.331 -0.089595 8.449 10.214
## 97 9.421 9.662 0.240512 8.752 10.571
## 98 9.421 9.157 -0.263947 8.168 10.147
## 99 9.421 9.542 0.121038 8.502 10.582
## 100 9.421 9.306 -0.115343 8.169 10.442
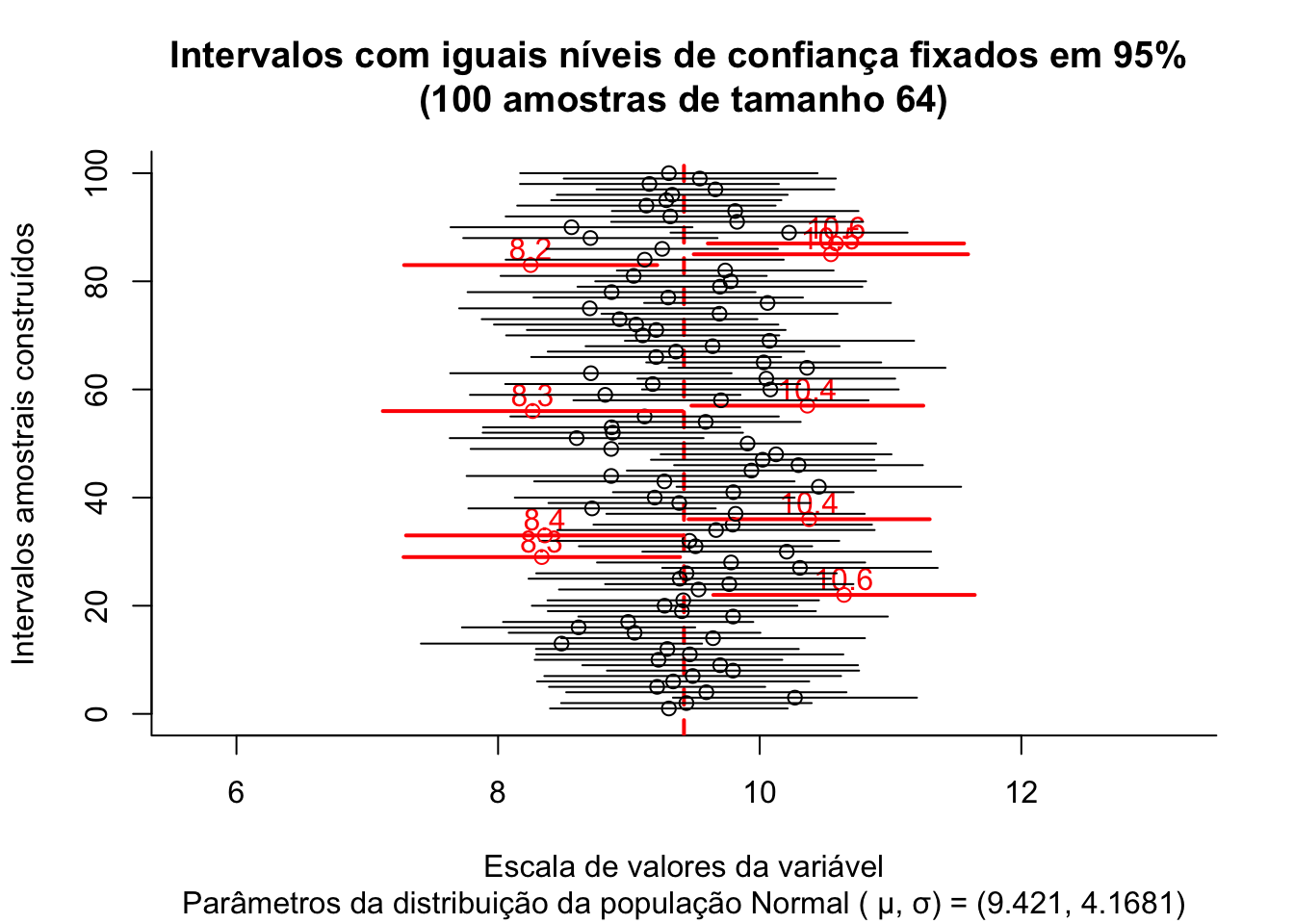
O gráfico acima expõe os intervalos de confiança: \((1-\alpha)\)=95% produzidos para as 100 médias de amostras de tamanho 64 extraídas de uma população com parâmetros \(\mu:\) 9.421 e \(\sigma:\) 4.1681.
A proporção de intervalos amostrais que não contém o verdadeiro valor do parâmetro populacional pode ser visualmente inspecionada pelas linhas em vermelho.
Intervalos de confiança bilaterais: intervalos delimitados por dois valores: mínimo e máximo, para a proporção amostral, dentro do qual todos os valores possuem um mesmo nível de confiança de ocorrência.
Intervalos de confiança unilaterais: intervalos delimitados apenas em um de seus lados, nos quais todos os valores possuem um mesmo nível de confiança. Podem ser limitados à direita por um valor máximo ou limitados à esquerda por um valor mínimo.