11.7 Estruturas das hipóteses

11.7.1 Interpretação gráfica dos níveis de significância/confiança

O delineamento de um teste de hipóteses inclui regras de decisão para se rejeitar ou não a hipótese nula.

Essas regras de decisão passam pela comparação dos valores calculados de uma estatística apropriada para o teste em curso com seus valores extremos, frequentemente obtidos em tabelas, os quais estão associados ao complemento de uma probabilidade (o nível de confiança) de ocorrência condizente ao nível de significância estabelecido na pesquisa.

Essa comparação é por demais facilitada se visualizada no gráfico da densidade de probabilidade da distribuição da estatística do teste, onde regiões (baseadas no nível de significância estabelecido) podem ser estabelecidas:

testes bilaterais ( hipótese alternativa do tipo: diferente de ): a região é fechada, delimitada à esquerda e à direita por valores críticos de estatística do teste;
testes unilaterais à direita ( hipótese alternativa do tipo: maior que ): a região é fecfada à esquerda, delimitada por um valor crítico da estatística do teste e aberta à direita (ao $\to \infty$); e,
testes unilaterais à esquerda ( hipótese alternativa do tipo: menor que ): a região é fechada à direita, delimitada por um valor crítico da estatística do teste e aberta à esquerda ($\to -\infty$).

No gráfico de densidade de probabilidade da estatística do teste temos uma primeira região frequentemente denominada de região de não rejeição: um intervalo de valores dentro do qual, se o valor calculado para a estatística de teste estiver contido, a hipótese nula não será rejeitada.

O intervalo de valores que delimitam a região de não rejeição é tal que a probabilidade dessa região é igual ao nível de confiança $(1-\alpha)$.

Se a estatística calculada para o teste estiver fora da faixa de valores delimitada na região de não rejeição a hipótese nula poderá ser rejeitada sob o nível de significância $\alpha$ estabelecido; ou seja, a probabilidade de se incorrer em um erro Tipo I: rejeitar a hipótese nula quando ela é verdadeira é igual a $\alpha$.

Com a popularização dos programas estatísticos computacionais, a probabilidade exata associada ao valor calculado da estatística do teste passou ser neles apresentada de modo default, nominada pela expressão valor p ( p-Value ) que expressa uma probabilidade.

Para melhor entender o valor-p ( p-value) suponha que o valor da estatística do teste seja igual a $\zeta$. O valor p é o quantil associado (a probabiliadde exata) a $\zeta$ na distribuição de probabilidade usada como referência. Se o valor p for menor que o nível de significância ($\alpha$) estipulado pelo pesquisador, rejeita-se a hipótese nula sob esse nível de significância de cometimento de um erro do tipo I.

11.7.2 Teste de hipóteses Bilateral

Nesse tipo de teste a hipótese aternativa é proposta como a dizer que o valor em teste é diferente daquele afirmado pela hipótese nula (conservadora):

\[ \begin{cases} H_{0}: \mu = \mu_{0}\\ H_{1}: \mu \ne \mu_{0}\\ \end{cases} \]

em que $\mu$ é o valor conservador do parâmetro que se deseja testar frente ao valor alternativo $\mu_{0}$.

alfa=0.05

prob_desejada1=alfa/2
z_desejado1=round(qnorm(prob_desejada1),4)
d_desejada1=dnorm(z_desejado1, 0, 1)

prob_desejada2=1-alfa/2
z_desejado2=round(qnorm(prob_desejada2),4)
d_desejada2=dnorm(z_desejado2, 0, 1)



ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores da estatística calculada para o teste")  +
  labs(title= 
         "Regiões críticas sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P((-val. crítc), (val. crít.))=(1-\u03b1) em cinza (nível de confiança) \nP(-\U221e; (-val. crític.))= P((val.crítc.); \U221e)= \u03b1/2 em vermelho ")+
  geom_segment(aes(x = z_desejado1, y = 0, xend = z_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = z_desejado2, y = 0, xend = z_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_desejado1-0.1, y=d_desejada1, label="-(valor crítico)", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.3, y=d_desejada2, label="(valor crítico)", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1-2, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.5, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Região de não rejeição da hipótese nula \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()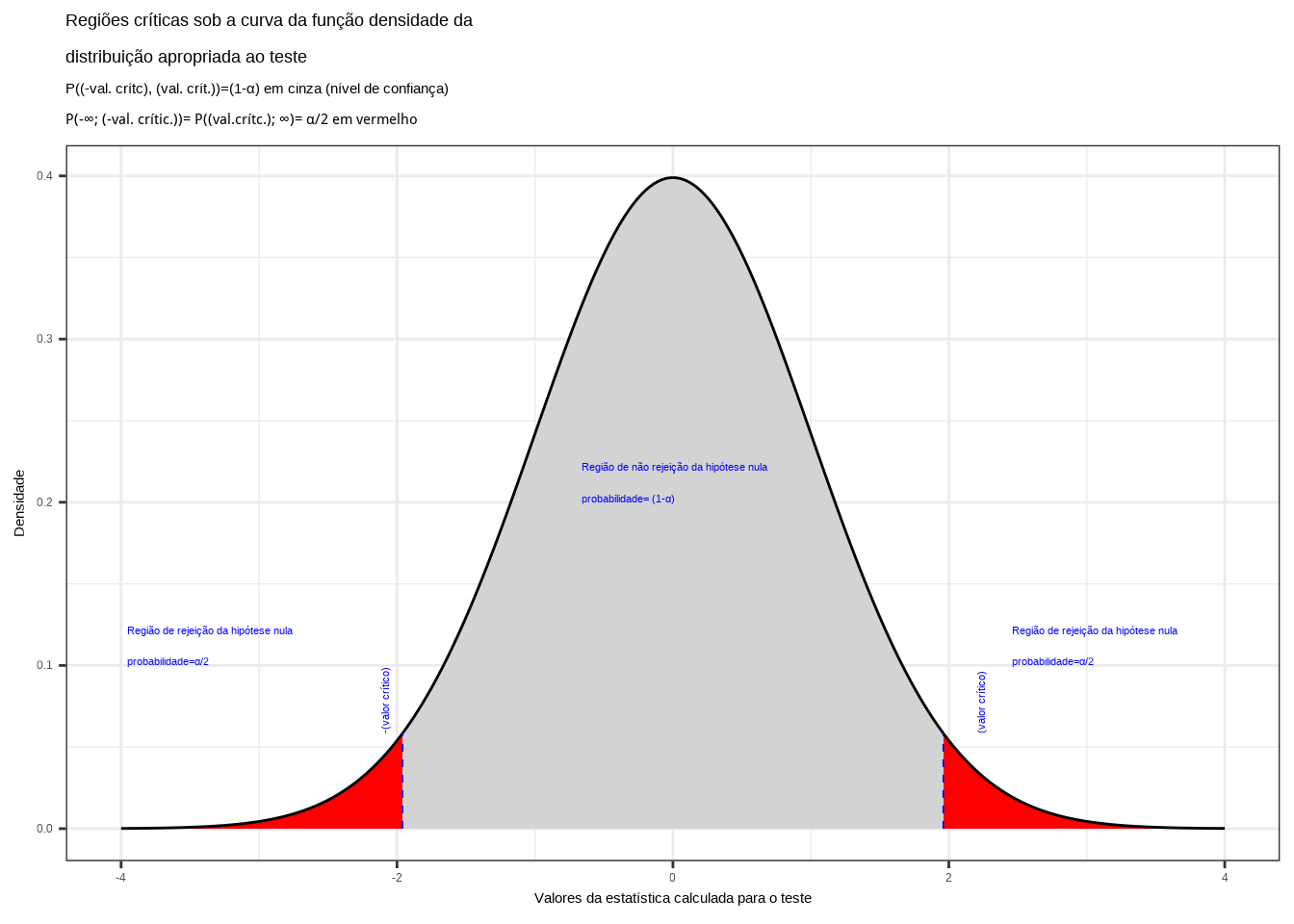

$Regiões críticas, aquém e além das quais, a probabilidade associada aos valores amostrais observados é inferior a $\frac{\alpha}{2}$, estabelecendo assim um intervalo com nível de confiança igual a $(1-\alpha)$$

Figure 11.8: Regiões críticas, aquém e além das quais, a probabilidade associada aos valores amostrais observados é inferior a $\frac{\alpha}{2}$, estabelecendo assim um intervalo com nível de confiança igual a $(1-\alpha)$

Na Figura 11.8 observa-se:

as regiões de rejeição da hipótese nula (subdivididas nos dois lados) sob a curva da função densidade de probabilidade da distribuição adequada ao teste com probabilidades iguais ao nível de significância $\alpha$ ;
a região de não rejeição da hipótese nula (delimitada à esquerda e à direita) com probabilidade igual ao nível de confiança $(1-\alpha)$; e,
os valores críticos da estatística do teste.

11.7.3 Teste de hipóteses Unilateral à esquerda

Nesse tipo de teste a hipótese aternativa é proposta como a dizer que o valor em teste não apenas é diferente, mas é menor do que aquele afirmado pela hipótese nula (conservadora):

\[ \begin{cases} H_{0}: \mu \ge \mu_{0}\\ H_{1}: \mu < \mu_{0}\\ \end{cases} \]

em que $\mu$ é o valor conservador do parâmetro que se deseja testar frente ao valor alternativo $\mu_{0}$.

alfa=0.05
prob_desejada=alfa
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)





ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores da estatística calculada para o teste")  +
  labs(title= 
         "Região crítica sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P( (-val. crít.),\U221e,)=(1-\u03b1) em cinza (nível de confiança) \nP(-\U221e; (-val. crític.))=\u03b1 em vermelho ")+
geom_segment(aes(x = z_desejado, y = 0, xend = z_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
annotate(geom="text", x=z_desejado-0.1, y=d_desejada, label="-(valor crítico)", angle=90, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado-2, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1", angle=0, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado+1.3, y=0.2, label="Região de não rejeição da hipótese nula  \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
theme_bw()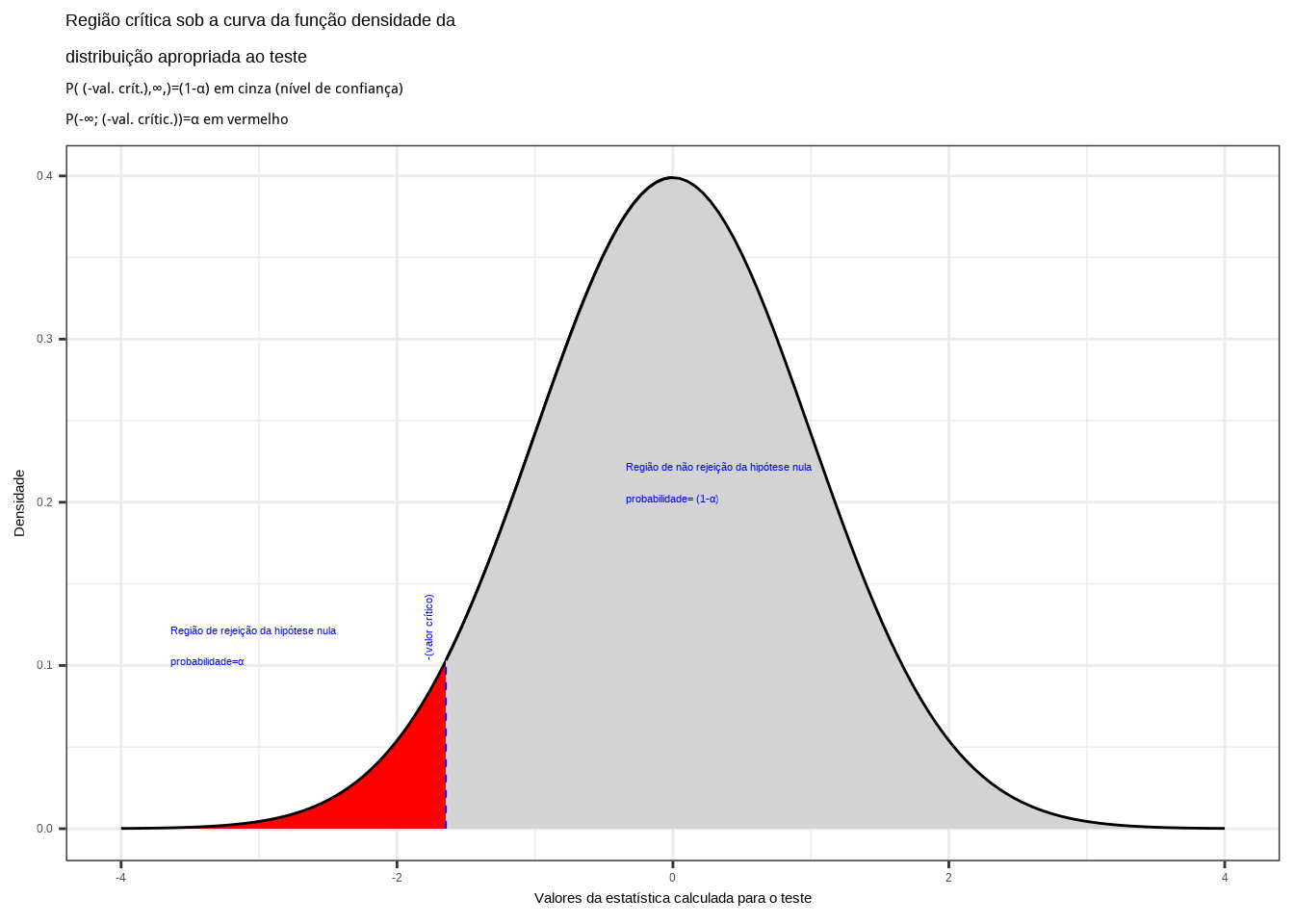

$Região crítica aquém da qual a probabilidade associada aos valores amostrais observados é inferior a $\alpha$, estabelecendo assim um intervalo com nível de confiança igual a $(1-\alpha)$$

Figure 11.9: Região crítica aquém da qual a probabilidade associada aos valores amostrais observados é inferior a $\alpha$, estabelecendo assim um intervalo com nível de confiança igual a $(1-\alpha)$

Na Figura 11.9 observa-se:

a região de rejeição da hipótese nula delimitada sob a curva da função densidade de probabilidade da distribuição adequada ao teste com probabilidade igual ao nível de significância $\alpha$ ;
a região de não rejeição da hipótese nula (delimitada à esquerda) com probabilidade igual ao nível de confiança $(1-\alpha)$; e,
os valores críticos da estatística do teste.

11.7.4 Teste de hipóteses Unilateral à direita

Nesse tipo de teste a hipótese aternativa é proposta como a dizer que o valor em teste não apenas é diferente, mas é maior do que aquele afirmado pela hipótese nula (conservadora):

\[ \begin{cases} H_{0}: \mu \le \mu_{0}\\ H_{1}: \mu > \mu_{0}\\ \end{cases} \]

em que $\mu$ é o valor conservador do parâmetro que se deseja testar frente ao valor alternativo $\mu_{0}$.

alfa=0.95
prob_desejada=alfa
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)




ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(-4, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores da estatística calculada para o teste")  +
  labs(title= 
         "Região crítica sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P(-\U221e, (val. crít.))=(1-\u03b1) em cinza (nível de confiança) \nP((val.crítc.); \U221e)= \u03b1 em vermelho ")+
geom_segment(aes(x = z_desejado, y = 0, xend = z_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
annotate(geom="text", x=z_desejado+0.3, y=d_desejada, label="(valor crítico)", angle=90, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado+0.5, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado-2.5, y=0.2, label="Região de não rejeição da hipótese nula \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()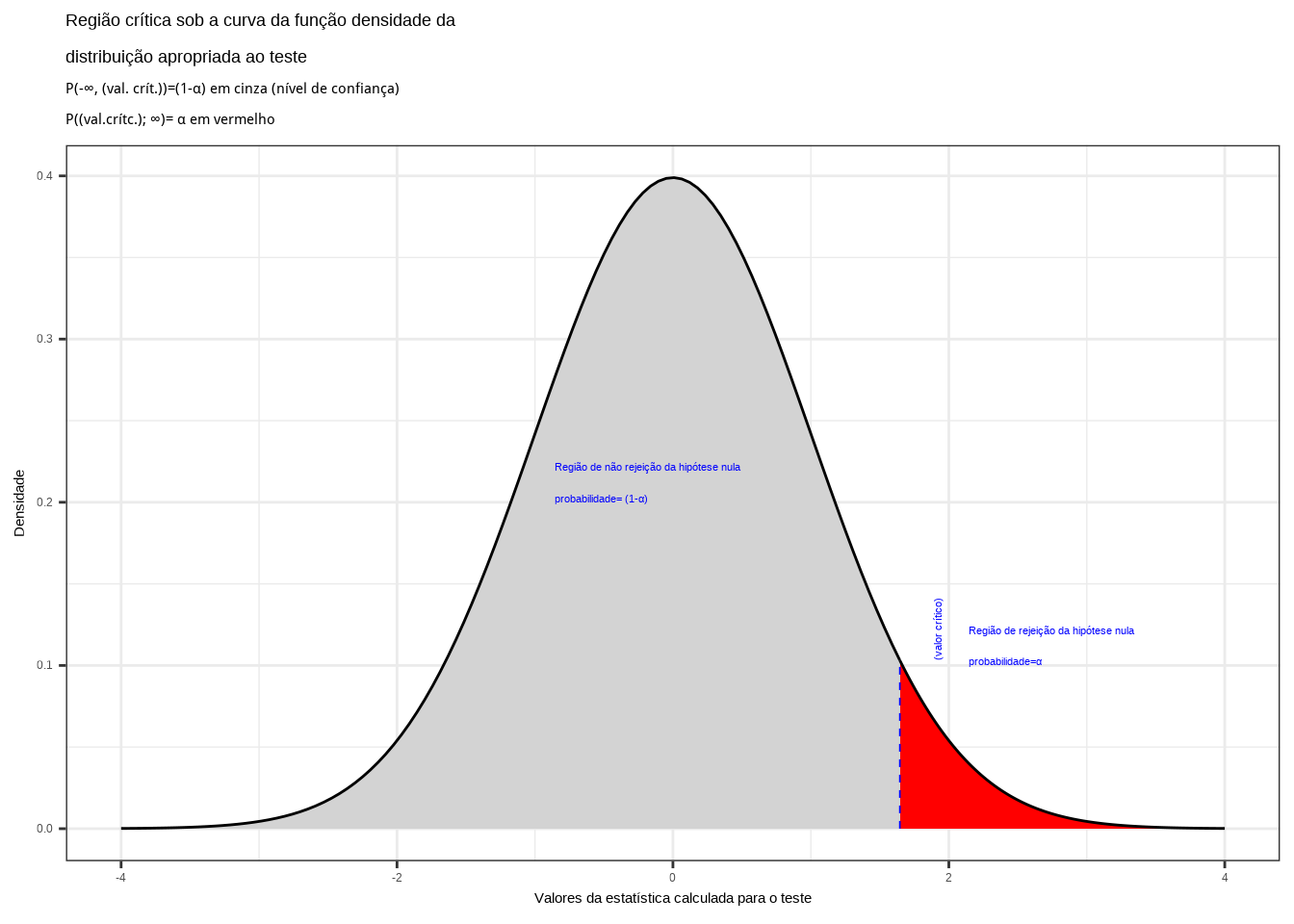

$Região crítica além da qual a probabilidade associada aos valores amostrais observados é inferior a $\alpha$, estabelecendo assim um intervalo com nível de confiança igual a $(1-\alpha)$$

Figure 11.10: Região crítica além da qual a probabilidade associada aos valores amostrais observados é inferior a $\alpha$, estabelecendo assim um intervalo com nível de confiança igual a $(1-\alpha)$

Na Figura 11.10 observa-se:

a região de rejeição da hipótese nula delimitada sob a curva da função densidade de probabilidade da distribuição adequada ao teste com probabilidade igual ao nível de significância $\alpha$ ;
a região de não rejeição da hipótese nula (delimitada à direita) com probabilidade igual ao nível de confiança $(1-\alpha)$; e,
os valores críticos da estatística do teste.