9.4 Distribuição das diferenças de médias amostrais independentes e seus intervalos de confiança

Consideremos duas populações \(X\) e \(Y\) com médias \(\mu_{1}\) e \(\mu_{2}\) e variâncias \(\sigma_{1}^{2}\) e \(\sigma_{2}^{2}\), respectivamente.

 

Conforme seções anteriores, as médias amostrais \(\stackrel{-}{X}\) e \(\stackrel{-}{Y}\) são duas variáveis aleatórias tais que:

\[\begin{align*} \stackrel{-}{X} & \sim N(\mu_{1}, \frac{\sigma^{2}_{1}}{n_{1}} )\\ \stackrel{-}{Y} & \sim N(\mu_{2}, \frac{\sigma^{2}_{2}}{n_{2}} ) \end{align*}\]

Pode-se demonstrar, pelas propriedades da esperança e da variância, que a média e a variância de uma variável aleatória (população) que resulta da soma ou diferença de duas outras, \(X\) e \(Y\), é:

\[\begin{align*} \mu_{(X \pm Y)} & = \mu_{1} \pm \mu_{2}\\ \sigma^{2}_{(X \pm Y)} & = \sigma_{1}^{2} + \sigma_{2}^{2} \end{align*}\]

E a média e variância da soma ou diferença das distribuições amostrais das médias de \(X\) e \(Y\) é:

\[\begin{align*} \mu_{(\stackrel{-}{X} \pm \stackrel{-}{Y})} & = \mu_{1} \pm \mu_{2} \\ \sigma^{2}_{(\stackrel{-}{X} \pm \stackrel{-}{Y})} & = \frac{\sigma_{1}^{2}}{n_{1}} + \frac{\sigma_{2}^{2}}{n_{2}} \end{align*}\]

9.4.1 Intervalos de confiança para a diferença entre duas médias amostrais com variância populacionais conhecidas

Se \((X_{1}, X_{2},...,X{n_{1}})\) e \((Y_{1}, Y_{2},...,Y{n_{2}})\) forem amostras aleatórias simples das populações \(X\) e \(Y\) com médias \(\mu_{1}\) e \(\mu_{2}\), e variâncias \(\sigma_{1}^{2}\) e \(\sigma_{2}^{2}\) conhecidas, e \(\stackrel{-}{X}=\frac{(X_{1}+X_{2}+...+X{n_{1}})}{n}\) e \(\stackrel{-}{Y}=\frac{(Y_{1}+Y_{2}+...+Y{n_{2}})}{n_{2}}\), então:

\[\begin{align*} {X} & \sim N( \mu_{1} , \frac{\sigma_{1}}{\sqrt{n_{1}}} ) \\ {Y} & \sim N( \mu_{2} , \frac{\sigma_{2}}{\sqrt{n_{2}}} ) \end{align*}\]

Demonstra-se que a diferença entre \(\stackrel{-}{X} e \stackrel{-}{Y}\) é tal que:

\[ \stackrel{-}{X} - \stackrel{-}{Y} \sim N((\mu_{1}-\mu_{2}) , \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } ) \]

Demonstra-se que a estatística \(Z\) pode ser assim definida, bem como sua correspondente distribuição (cf.Figura 9.20):

\[ Z = \frac{ (\stackrel{-}{X}-\stackrel{-}{Y}) - (\mu_{1}-\mu_{2})}{ \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } } \sim N(0 ,1) \]

em que:

• \(\stackrel{-}{X}\)e \(\stackrel{-}{Y}\) são as médias amostrais;
  
• \(\mu_{1}\) e \(\mu_{2}\) são as médias populacionais;
  
• \(\sigma_{1}^{2}\) e \(\sigma_{2}^{2}\) são as variâncias populacionais; e,
• \(n_{1}\) e \(n_{2}\) são os tamanhos das amostras

alfa=0.05

prob_desejada1=alfa/2
z_desejado1=round(qnorm(prob_desejada1),4)
d_desejada1=dnorm(z_desejado1, 0, 1)

prob_desejada2=1-alfa/2
z_desejado2=round(qnorm(prob_desejada2),4)
d_desejada2=dnorm(z_desejado2, 0, 1)




ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``z'' da distribuição Normal padrão")  +
  labs(title= 
         "Curva da função densidade \nDistribuição Normal Padrão", 
       subtitle = "P(-z; z)=(1-\u03b1) em cinza (nível de confiança) \nP(-\U221e; -z)= P(z; \U221e)= \u03b1/2 em vermelho")+
  geom_segment(aes(x = z_desejado1, y = 0, xend = z_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = z_desejado2, y = 0, xend = z_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_desejado1-0.1, y=d_desejada1, label="-z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado2+0.3, y=d_desejada2, label="z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado1-1.8, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.5, y=0.1, label="Intervalo aberto à dir. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Intervalo fechado \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()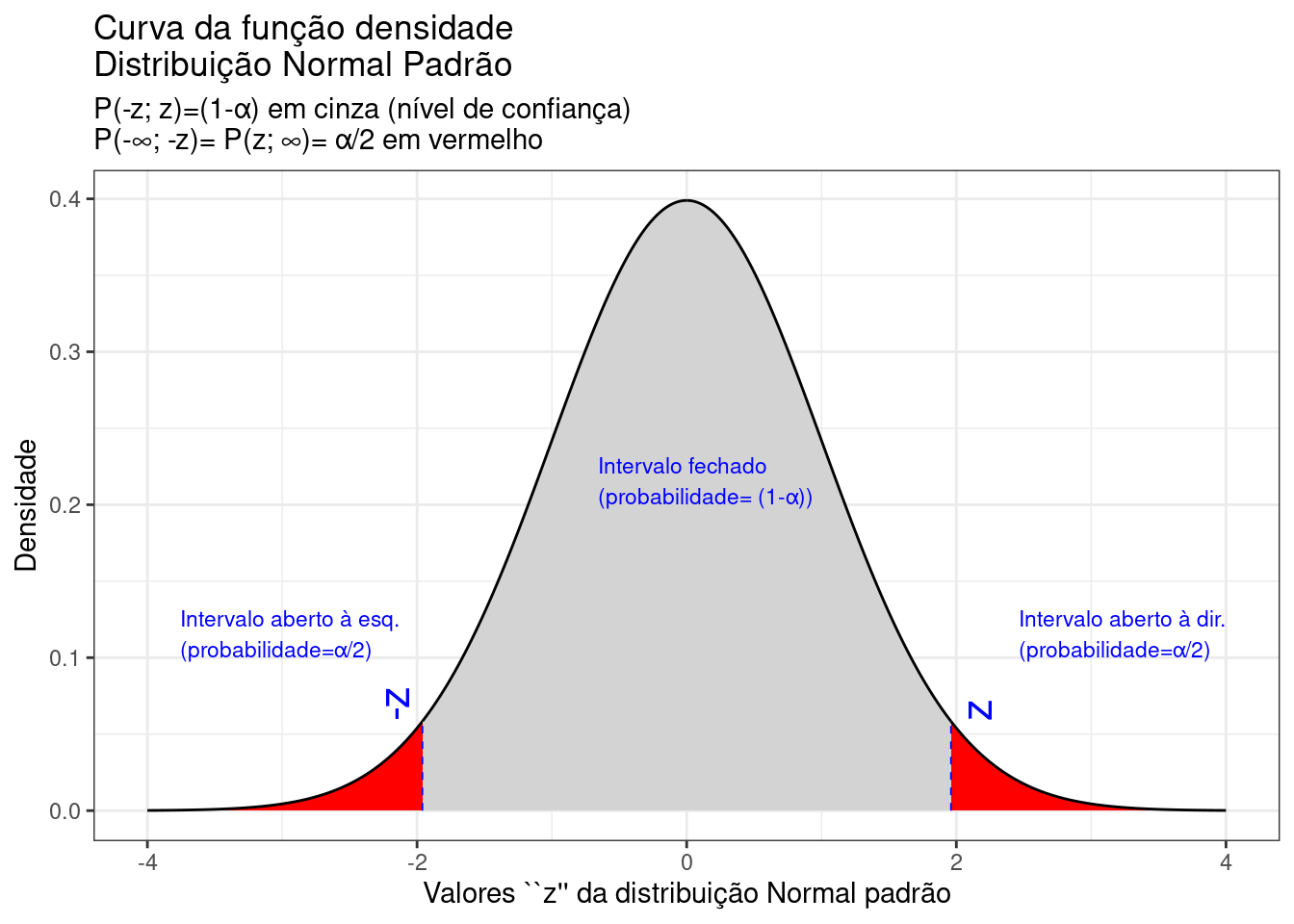

Figure 9.20: Regiões críticas, aquém e além das quais, a probabilidade associada aos valores da estatística \(Z\) é inferior a \(\frac{\alpha}{2}\), estabelecendo assim um intervalo com nível de confiança igual a \((1-\alpha)\)

Na Figura 9.20 observa-se:

 

• o nível de significância \(\alpha\);
  
• o nível de confiança \((1-\alpha)\); e,
  
• o valor tabelado da estatística \(Z(z)\) para o nível de confiança fixado.

Assim,

\[\begin{align*} P\left[-{Z}_{(1-\frac{\alpha }{2})}\le Z \le {Z }_{(1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P\left[-{z}_{(1-\frac{\alpha }{2})}\le \frac{ (\stackrel{-}{x}-\stackrel{-}{y}) - (\mu_{1}-\mu_{2})}{ \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } } \le {z}_{(1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P[(\stackrel{-}{x}-\stackrel{-}{y} ) - ({z}_{(1-\frac{\alpha }{2})} \cdot \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } ) \le (\mu_{1}-\mu_{2}) \le (\stackrel{-}{x}-\stackrel{-}{y}) +({z}_{(1-\frac{\alpha }{2})} \cdot \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } ) ] & = (1-\alpha) \end{align*}\]

 

\[ IC(\mu_{1}-\mu_{2})_{(1-\alpha)}=[ (\stackrel{-}{x}-\stackrel{-}{y} ) \pm {z}_{c} \cdot \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } ] \]

Exemplo: Uma empresa possui duas filiais (A e B). Uma amostra das vendas de 20 dias forneceu uma venda média diária de 40 unidades dessa peça a filial A e de 30 unidades da mesma peça para a filial B. Os desvios padrão das vendas diárias dessa peça são de 5 e 3, respectivamente. Admitindo que a distribuição diária das vendas dessa peça siga uma distribuição Normal, qual o intervalo de confiança para a diferença de médias das vendas nas duas filiais com um nível de confiança de 95%?

Dados do problema:

• \(\stackrel{-}{X}=40\) e \(\stackrel{-}{Y}=30\) são as médias amostrais (vendas médias diárias nas filiais A e B, respectivamente);
  
• \(\sigma_{1}^{2}=25\) e \(\sigma_{2}^{2}=9\) são as variâncias populacionais;
  
• \(n_{1} = n_{2}=20\) são os tamanhos das amostras; e,
• valor extraído da tabela \(z=1,96\) correspondente ao nível de confiança estipulado \((1-\alpha)=95\%\).

\[\begin{align*} P[(\stackrel{-}{x}-\stackrel{-}{y} ) - ({z}_{(1-\frac{\alpha }{2})} \cdot \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } ) \le (\mu_{1}-\mu_{2}) \le (\stackrel{-}{x}-\stackrel{-}{y}) +({z}_{(1-\frac{\alpha }{2})} \cdot \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } ) ] & =(1-\alpha) \\ P[(\stackrel{-}{x}-\stackrel{-}{y} ) - ({z}_{(1-\frac{\alpha }{2})} \cdot \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } ) \le (\mu_{1}-\mu_{2}) \le (\stackrel{-}{x}-\stackrel{-}{y}) +({z}_{(1-\frac{\alpha }{2})} \cdot \sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}} } ) ] & = (1-\alpha) \\ P[10 - ( 1,96 \cdot \sqrt{\frac{25}{20} + \frac{9}{20}} ) \le (\mu_{1}-\mu_{2}) \le ( 10 + ( 1,96 \cdot \sqrt{\frac{25}{20} + \frac{9}{20} } ) ] & = 0,95 \\ P[10 - (1,96 \times 1,3038) \le (\mu_{1}-\mu_{2}) \le 10 + (1,96 \times 1,3038) ] & = 0,95 \end{align*}\]

 

\[ IC (\mu_{1} - \mu_{2})_{0,95} = [7; 13] \]

Se quisermos ser rigorosos na interpretação do intervalo de confiança calculado podemos explicar que, se extrairmos um grande número de amostras dessas mesmas dimensões das vendas dessa peça nas duas empresas, e para cada uma delas calcularmos suas médias e as diferenças entre elas, e calcularmos os intervalos de confiança como o acima definido, a proporção desses intervalos onde podemos encontrar a diferença das médias de vendas dessa peça da filial A para a filial B será de 0,95 (95 intervalos em 100).

De uma forma mais sintética podemos afirmar que, o anterior intervalo aleatório [7 ; 13], é um intervalo de confiança a 95% para a diferença das médias de vendas dessa peça nas duas empresa

De uma forma mais corrente, embora menos correta em termos teóricos, é usual afirmar que, com 95% de confiança a diferença das médias de vendas dessa peça da filial A para a filial B se situa entre os valores 7 e 13.

Uma segunda observação se faz pertinente e se refere à natureza dos dados analisados e a forma de apresentação do resultado. Por serem dados discretos, o intervalo de confiança deverá ser apresentado em igual forma, sem ultrapassar os limites estabelecidos. Isto posto: \(IC (\mu_{1} - \mu_{2})_{0,95} = [7; 13]\) .

9.4.2 Intervalos de confiança para a diferença entre duas médias amostrais com variâncias populacionais desconhecidas mas admitidas iguais

Se \((X_{1}, X_{2},...,X{n_{1}})\) e \((Y_{1}, Y_{2},...,Y{n_{2}})\) forem amostras aleatórias simples das populações \(X\) e \(Y\) com médias \(\mu_{1}\) e \(\mu_{2}\), e variâncias \(\sigma_{1}^{2}\) e \(\sigma_{2}^{2}\) desconhecidas porém iguais (\(\sigma_{1}^{2}=\sigma_{2}^{2}=\sigma^{2}\)), e \(\stackrel{-}{X}=\frac{(X_{1}+X_{2}+...+X{n_{1}})}{n}\) e \(\stackrel{-}{Y}=\frac{(Y_{1}+Y_{2}+...+Y{n_{2}})}{n_{2}}\), então:

 

\[\begin{align*} {X} & \sim N( \mu_{1} , \frac{\sigma}{\sqrt{n_{1}}} )\\ {Y} & \sim N( \mu_{2} , \frac{\sigma}{\sqrt{n_{2}}} ) \end{align*}\]

Demonstra-se que a estatística \(T\) pode ser assim definida, bem como sua correspondente distribuição (cf. Figura \(\ref{fig62}\)):

\[ T = \frac{ (\stackrel{-}{X}-\stackrel{-}{Y}) - (\mu_{1}-\mu_{2})}{S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } } \sim t(n_{1}+n_{2}-2) \]

em que:

• \(\stackrel{-}{X}\)e \(\stackrel{-}{Y}\) são as médias amostrais;
  
• \(S_{1}^{2}\) e \(S_{2}^{2}\) são as variâncias amostrais;
  
• \(\mu_{1}\) e \(\mu_{2}\) são as médias populacionais;
  
• \(S_{p}\) é um desvio padrão amostral ponderado para as duas amostras;
  
• \(n_{1}\) e \(n_{2}\) são os tamanhos das amostras;

O desvio padrão ponderado \(S_{p}\) é dado por:

\[ S_{p} = \sqrt{\frac{(n_{1}-1)\cdot S^{2}_{1} + (n_{2}-1)\cdot S^{2}_{2}}{n_{1}+n_{2}-2}} \]

alfa=0.05

prob_desejada1=alfa/2
df=20
t_desejado1=round(qt(prob_desejada1,df ),4)
d_desejada1=dt(t_desejado1,df)

prob_desejada2=1-alfa/2
df=20
t_desejado2=round(qt(prob_desejada2, df),4)
d_desejada2=dt(t_desejado2,df)



ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dt,
            args=list(df), 
            fill = "red", 
            xlim = c(-4, t_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(t_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(0, t_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "red", 
            xlim = c(t_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``t'' da distribuição de Student")  +
  labs(title= "Curva da função densidade \nDistribuição t (df=20)", 
       subtitle = "P(-t; t)=(1-\u03b1) em cinza (nível de confiança) \nP(-\U221e; -t)= P(t; \U221e)= \u03b1/2 em vermelho ")+
  geom_segment(aes(x = t_desejado1, y = 0, xend = t_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = t_desejado2, y = 0, xend = t_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=t_desejado1-0.1, y=d_desejada1, label="-t", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=t_desejado2+0.3, y=d_desejada2, label="t", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=t_desejado1-1.8, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado2+0.5, y=0.1, label="Intervalo aberto à dir. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado1+1.3, y=0.2, label="Intervalo fechado \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+  theme_bw()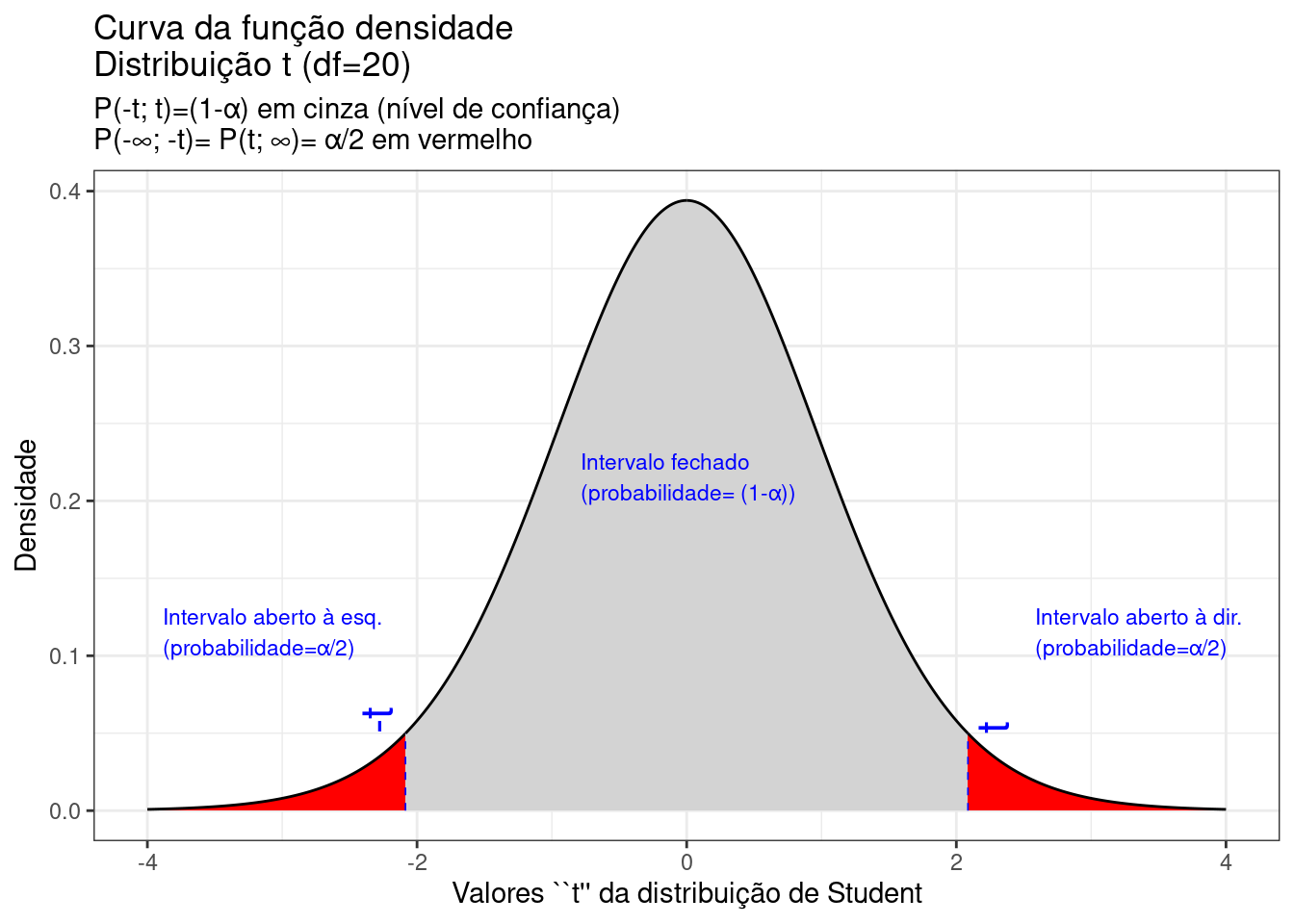

Figure 9.21: Regiões críticas, aquém e além das quais, a probabilidade associada aos valores da estatística \(T\) (\((n-1)\) graus de liberdade) é inferior a \(\frac{\alpha}{2}\), estabelecendo assim um intervalo com nível de confiança igual a \((1-\alpha)\)

Na Figura 9.21 observa-se:

 

• o nível de significância \(\alpha\);
  
• o nível de confiança \((1-\alpha)\); e,
  
• o valor tabelado da estatística \(T(t)\) sob \((n_{1}+n_{2}-2)\) graus de liberdade para o nível de confiança fixado.

 

Assim,

 

\[\begin{align*} P\left[-{T}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})}\le T \le {T}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P\left[-{t}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})}\le \frac{ (\stackrel{-}{x}-\stackrel{-}{y}) - (\mu_{1}-\mu_{2})}{S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } } \le {t}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})}\right] & =(1-\alpha) \\ P[(\stackrel{-}{x}-\stackrel{-}{y} ) - ({t}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})} \cdot S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } ) \le (\mu_{1}-\mu_{2}) \le (\stackrel{-}{x}-\stackrel{-}{y}) +({t}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})} \cdot S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } ) ] & =(1-\alpha) \end{align*}\]

\[ IC(\mu_{1}-\mu_{2})_{(1-\alpha)}=[ (\stackrel{-}{x}-\stackrel{-}{y} ) \pm {t}_{c(n_{1}+n_{2}-2)} \cdot S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } ] \]

Exemplo: De uma grande turma extraiu-se uma pequena amostra de quatro notas de uma prova: 64, 66, 89, 77. De uma outra turma, extraiu-se uma outra amostra, independente, de três notas: 56, 71, 53. Se for razoável admitir que as variâncias das duas turmas (\(\sigma^{2}_{1}\) e \(\sigma^{2}_{2}\)) sejam iguais, qual seria o intervalo de confiança para a diferença observada entre essas médias, a um nível de confiança de 95%?

Dados do problema:

 

• \(\stackrel{-}{X}=74\) e \(\stackrel{-}{Y}=60\) são as médias calculadas sobre as duas amostras (notas nas turmas);
  
• \(S_{1}^{2}=132,67\) e \(S_{2}^{2}=93\) são as variâncias calculadas sobre as duas amostras;
• \(n_{1} = 4\) e \(n_{2}=3\) são os tamanhos das amostras;
  
• \(n_{1}+ n_{2}-2=5\) são os graus de liberdade; e,
• \(t=2,57\) o valor tabelado da estatística para um nível de significância \(\alpha=5\%\) e graus de liberdade \(gl=5\).

\[\begin{align*} P[(\stackrel{-}{x}-\stackrel{-}{y} ) - ({t}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})} \cdot S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } ) \le (\mu_{1}-\mu_{2}) \le (\stackrel{-}{x}-\stackrel{-}{y}) +({t}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})} \cdot S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } ) ]=(1-\alpha) \end{align*}\]

O desvio padrão ponderado \(S_{p}\) é dado por:

\[\begin{align*} S_{p} & = \sqrt{\frac{(n_{1}-1)\cdot S^{2}_{1} + (n_{2}-1)\cdot S^{2}_{2}}{n_{1}+n_{2}-2}} \\ S_{p} & = \sqrt{\frac{( 4-1)\cdot 132,67 + ( 3 -1)\cdot 93 }{4 + 3 - 2}} \\ S_{p} & = 10,81 \end{align*}\]

\[\begin{align*} P[(\stackrel{-}{x}-\stackrel{-}{y} ) - ({t}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})} \cdot S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } ) \le (\mu_{1}-\mu_{2}) \le (\stackrel{-}{x}-\stackrel{-}{y}) +({t}_{(n_{1}+n_{2}-2, 1-\frac{\alpha }{2})} \cdot S_{p} \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } ) ] & = (1-\alpha) \\ P[ 14 - ( 2,57 \cdot 10,81 \cdot \sqrt{\frac{1}{4} + \frac{1}{3} } ) \le (\mu_{1}-\mu_{2}) \le 14 +( 2,57 \cdot 10,81 \cdot \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}} } ) ] & = 0,95 \\ P[ 14 - 21,23 \le (\mu_{1}-\mu_{2}) \le 14 + 21,23 ] & =0,95 \end{align*}\]

\[ IC (\mu_{1} - \mu_{2})_{0,95} = [-7,23; 35,23 ] \]

Se quisermos ser rigorosos na interpretação do intervalo de confiança calculado podemos explicar que, se extrairmos um grande número de amostras dessas mesmas dimensões das vendas dessa peça nas duas empresas, e para cada uma delas calcularmos suas médias e as diferenças entre elas, e calcularmos os intervalos de confiança como o acima definido, a proporção desses intervalos onde podemos encontrar a diferença das médias de vendas dessa peça da filial A para a filial B será de 0,95 (95 intervalos em 100).

De uma forma mais sintética podemos afirmar que o intervalo aleatório [-7,23; 35,23], é um intervalo de confiança a 95% para a diferença das médias das notas dessas provas nas duas turmas.

De uma forma mais corrente, embora menos correta em termos teóricos, é usual afirmar que, com 95% de confiança a diferença das médias das notas da primeira turma para a segunda turma se situa entre os valores -7,23 e 35,23.

Uma importante conclusão pode ser extraída ao se analisar um pouco mais atentamente o intervalo calculado [-7,23 ; 35,23]. Vê-se que encontra-se dentro desse intervalo o valor 0 indicando que a diferença entre as médias amopstrais pode ser zero sob esse nível de confiança, o que equivale dizer que sob esse nível de confiança não se pode afirmar existir diferença significativa (i.e. sob o nível de significância) entre as médias das notas dessas duas turmas.

9.4.3 Intervalos de confiança para a diferença entre duas médias amostrais com variâncias populacionais desconhecidas e desiguais

Se \((X_{1}, X_{2},...,X{n_{1}})\) e \((Y_{1}, Y_{2},...,Y{n_{2}})\) forem amostras aleatórias simples das populações \(X\) e \(Y\) com médias \(\mu_{1}\) e \(\mu_{2}\), e variâncias \(\sigma_{1}^{2}\) e \(\sigma_{2}^{2}\) desconhecidas porém iguais (\(\sigma_{1}^{2}=\sigma_{2}^{2}=\sigma^{2}\)), e \(\stackrel{-}{X}=\frac{(X_{1}+X_{2}+...+X{n_{1}})}{n}\) e \(\stackrel{-}{Y}=\frac{(Y_{1}+Y_{2}+...+Y{n_{2}})}{n_{2}}\), então:

 

\[\begin{align*} {X} & \sim N( \mu_{1} , \frac{\sigma}{\sqrt{n_{1}}} ) \\ {Y} & \sim N( \mu_{2} , \frac{\sigma}{\sqrt{n_{2}}} ) \end{align*}\]

Demonstra-se que a estatística \(T\) pode ser assim definida, bem como sua correspondente distribuição (cf. Figura \(\ref{fig63}\)):

 

\[ T = \frac{ (\stackrel{-}{X}-\stackrel{-}{Y}) - (\mu_{1}-\mu_{2})}{ \sqrt{\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}}}} \sim t_{\nu} \]

 

em que:

 

• \(\stackrel{-}{X}\)e \(\stackrel{-}{Y}\) são as médias das amostras extraídas;
• \(\mu_{1}\) e \(\mu_{2}\) são as médias populacionais;
  
• \(n_{1}\) e \(n_{2}\) são os tamanhos das amostras; e,
• \(S_{1}^{2}\) e \(S_{2}^{2}\) são as variâncias das amostras.

O número de graus de liberdade (\(\nu\)) é dado por:

 

\[ \nu = \frac{ (\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}})^{2} } { \frac{(\frac{S^{2}_{1}}{n_{1}})^{2}}{n_{1}-1} + \frac{(\frac{S^{2}_{2}}{n_{2}})^{2}}{n_{2}-1} } \]

alfa=0.05

prob_desejada1=alfa/2
df=20
t_desejado1=round(qt(prob_desejada1,df ),4)
d_desejada1=dt(t_desejado1,df)

prob_desejada2=1-alfa/2
df=20
t_desejado2=round(qt(prob_desejada2, df),4)
d_desejada2=dt(t_desejado2,df)



ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dt,
            args=list(df), 
            fill = "red", 
            xlim = c(-4, t_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(t_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(0, t_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "red", 
            xlim = c(t_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``t'' da distribuição de Student")  +
  labs(title= "Curva da função densidade \nDistribuição t (df=20)", 
       subtitle = "P(-t; t)=(1-\u03b1) em cinza (nível de confiança) \nP(-\U221e; -t)= P(t; \U221e)= \u03b1/2 em vermelho ")+
  geom_segment(aes(x = t_desejado1, y = 0, xend = t_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = t_desejado2, y = 0, xend = t_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=t_desejado1-0.1, y=d_desejada1, label="-t", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=t_desejado2+0.3, y=d_desejada2, label="t", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=t_desejado1-1.8, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado2+0.5, y=0.1, label="Intervalo aberto à dir. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado1+1.3, y=0.2, label="Intervalo fechado \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+  theme_bw()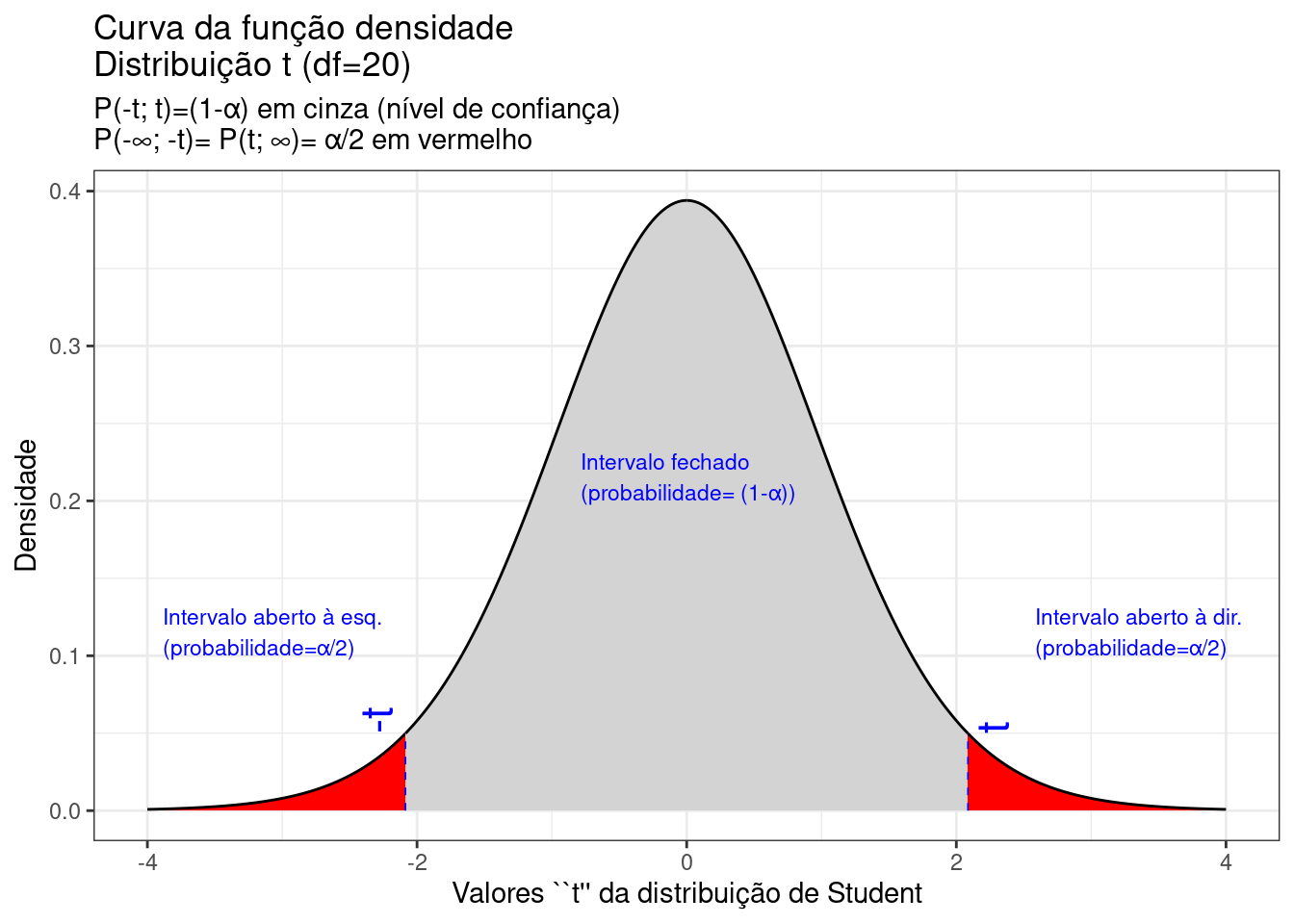

Figure 9.22: Regiões críticas, aquém e além das quais, a probabilidade associada aos valores da estatística \(T\) (com \(\nu\) graus de liberdade) é inferior a \(\frac{\alpha}{2}\), estabelecendo assim um intervalo com nível de confiança igual a \((1-\alpha)\)

Na Figura 9.22 observa-se:

 

• o nível de significância \(\alpha\);
  
• o nível de confiança \((1-\alpha)\); e,
  
• o valor tabelado da estatística \(T(t)\) sob \(\nu\) graus de liberdade para o nível de confiança fixado.

Assim,

\[\begin{align*} P\left[-{T}_{(\nu, 1-\frac{\alpha }{2})}\le T \le {T}_{( \nu, 1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P\left[-{t}_{( \nu, 1-\frac{\alpha }{2})}\le \frac{ (\stackrel{-}{x}-\stackrel{-}{y}) - (\mu_{1}-\mu_{2})}{\sqrt{\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}} } } \le {t}_{( \nu, 1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P[(\stackrel{-}{x}-\stackrel{-}{y} ) - ({t}_{( \nu, 1-\frac{\alpha }{2})} \cdot \sqrt{\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}} } ) \le (\mu_{1}-\mu_{2}) \le (\stackrel{-}{x}-\stackrel{-}{y}) +({t}_{( \nu, 1-\frac{\alpha }{2})} \cdot \sqrt{\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}} } ) ] & = (1-\alpha) \end{align*}\]

\[ IC(\mu_{1}-\mu_{2})_{(1-\alpha)} = [(\stackrel{-}{x}-\stackrel{-}{y} ) \pm {t}_{c (\nu)} \cdot \sqrt{\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}} } ] \]

Exemplo: De uma pequena classe do curso de ensino médio tomou-se uma amostra de 4 provas de matemática, obtendo-se um valor médio de 81 sob uma variância de 2. Outra amostra, de 6 provas de biologia, forneceu um valor médio de 77 sob uma variância de 14,4. Qual seria o intervalo de confiança para a diferença observada entre essas médias, sob um nível de confiança de 95%?

Dados do problema:

 

Dados do problema:

 

• \(\stackrel{-}{X}=81\) e \(\stackrel{-}{Y}=77\) são as médias calculadas sobre as duas amostras (notas nas turmas);
  
• \(S_{1}^{2}=2\) e \(S_{2}^{2}=14,40\) são as variâncias calculadas sobre as duas amostras;e,
• \(n_{1} = 4\) e \(n_{2}=6\) são os tamanhos das amostras.

O número de graus de liberdade (\(\nu\)) é dado por:

\[\begin{align*} \nu & = \frac{ (\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}})^{2} } { \frac{(\frac{S^{2}_{1}}{n_{1}})^{2}}{n_{1}-1} + \frac{(\frac{S^{2}_{2}}{n_{2}})^{2}}{n_{2}-1} } \\ \nu & = \frac{ (\frac{2}{4} + \frac{14,40}{6})^{2}}{\frac{(\frac{2}{4})^{2}}{4-1} + \frac{(\frac{14,40}{6})^{2}}{6-1} } \\ \nu & = \frac{ 2,90^{2}}{0,083 + 1,152} \\ \nu & = \frac{ 8,41}{1,23} = 6,83 \sim 7 \\ \end{align*}\]

Portanto, \(t=2,36\) é o valor tabelado da estatística para um nível de significância \(\alpha=5\%\) e graus de liberdade \(gl=7\).

\[\begin{align*} P[(\stackrel{-}{x}-\stackrel{-}{y} ) - ({t}_{( \nu, 1-\frac{\alpha }{2})} \cdot \sqrt{\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}} } ) \le (\mu_{1}-\mu_{2}) \le (\stackrel{-}{x}-\stackrel{-}{y}) +({t}_{( \nu, 1-\frac{\alpha }{2})} \cdot \sqrt{\frac{S^{2}_{1}}{n_{1}} + \frac{S^{2}_{2}}{n_{2}} } ) ] & = (1-\alpha) \\ P[ 4 - ( 2,36 \cdot \sqrt{\frac{ 2}{4} + \frac{14,40}{6}} ) \le (\mu_{1}-\mu_{2}) \le 4 +( 2,36 \cdot \sqrt{\frac{ 2}{4} + \frac{14,40}{6}} ) ] & = 0,95 \\ P[ 4 - ( 2,36 \cdot 1,70 ) \le (\mu_{1}-\mu_{2}) \le 4 +( 2,36 \cdot 1,70 ) ] & = 0,95 \\ P[ 4 - 4,01 \le (\mu_{1}-\mu_{2}) \le 4 + 4,01 ) ] & = 0,95 \\ \end{align*}\]

\(IC (\mu_{1} - \mu_{2})_{0,95} = [-0,01 ; 8,01]\)

Se quisermos ser rigorosos na interpretação do intervalo de confiança calculado podemos explicar que, se extrairmos um grande número de amostras dessas mesmas dimensões das notas dessas provas nas duas turmas, e para cada uma delas calcularmos suas médias e as diferenças entre elas, e calcularmos os intervalos de confiança como o acima definido, a proporção desses intervalos onde podemos encontrar a diferença das notas notas da prova de matemática para a prova de biologia será de 0,95 (95 intervalos em 100).

De uma forma mais sintética podemos afirmar que, o anterior intervalo aleatório [-0,01; 8,01], é um intervalo de confiança a 95% para a diferença das médias das notas dessas provas nas duas turmas.

De uma forma mais corrente, embora menos correta em termos teóricos, é usual afirmar que, com 95% de confiança a diferença das médias das notas da prova de matemática para a prova de biologia situa entre os valores -0,01 e 8,01.

Uma importante conclusão pode ser extraída ao se analisar um pouco mais atentamente o intervalo calculado [-0,01 ; 8,01]. Vê-se que encontra-se dentro desse intervalo o valor 0 indicando que a diferença entre as médias amopstrais pode ser zero sob esse nível de confiança, o que equivale dizer que sob esse nível de confiança não se pode afirmar existir diferença significativa (i.e. sob o nível de significância) entre as médias dessas notas.