2.9 Análise combinatória (métodos de enumeração)

A análise combinatória (ou métodos de enumeração) é um conjunto de técnicas para agrupamento de objetos conforme regras definidas e obtenção, através de cálculos, do número de agrupamentos possíveis.

2.9.1 Princípio básico da contagem (regra da multiplicação)

Suponha a realização de dois experimentos. Se o experimento \(E\) pode gerar qualquer um de \(n\) resultados possíveis (\(E_{1},E_{2},E_{3}, \dots, E_{n}\)) e se, para cada um dos resultados do experimento, houver \(m\) resultados possíveis para o experimento \(F\) (\(F_{1},F_{2},F_{3}, \dots, F_{m}\)), então os dois experimentos possuem conjuntamente \(n \cdot m\) diferentes resultados possíveis.

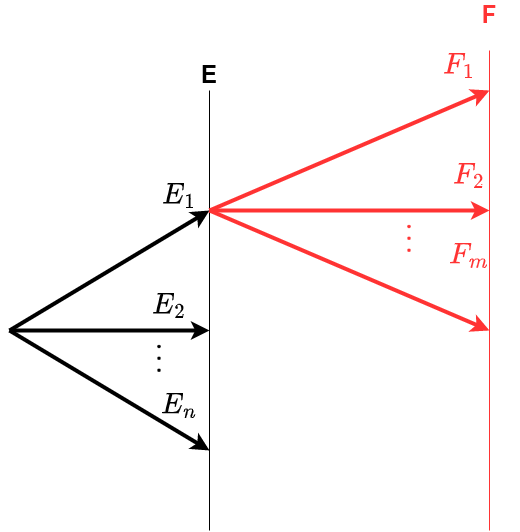
Figure 2.7: Regra da multiplicação

Esse princípio recebe o nome de Princípio multiplicativo, e é aplicado nos casos em que os eventos são interligados pelo conectivo e, característico de decisões sucessivas: ocorrem os dois.

Se um homem tem 2 camisas e 4 gravatas, então ele tem \(2 \times 4 = 8\) formas de combinar uma camisa com uma gravata.

Um diagrama como ilustrado na Figura 2.8 (denominado diagrama de árvore em virtude de sua aparência) geralmente é usado para explicar o princípio acima

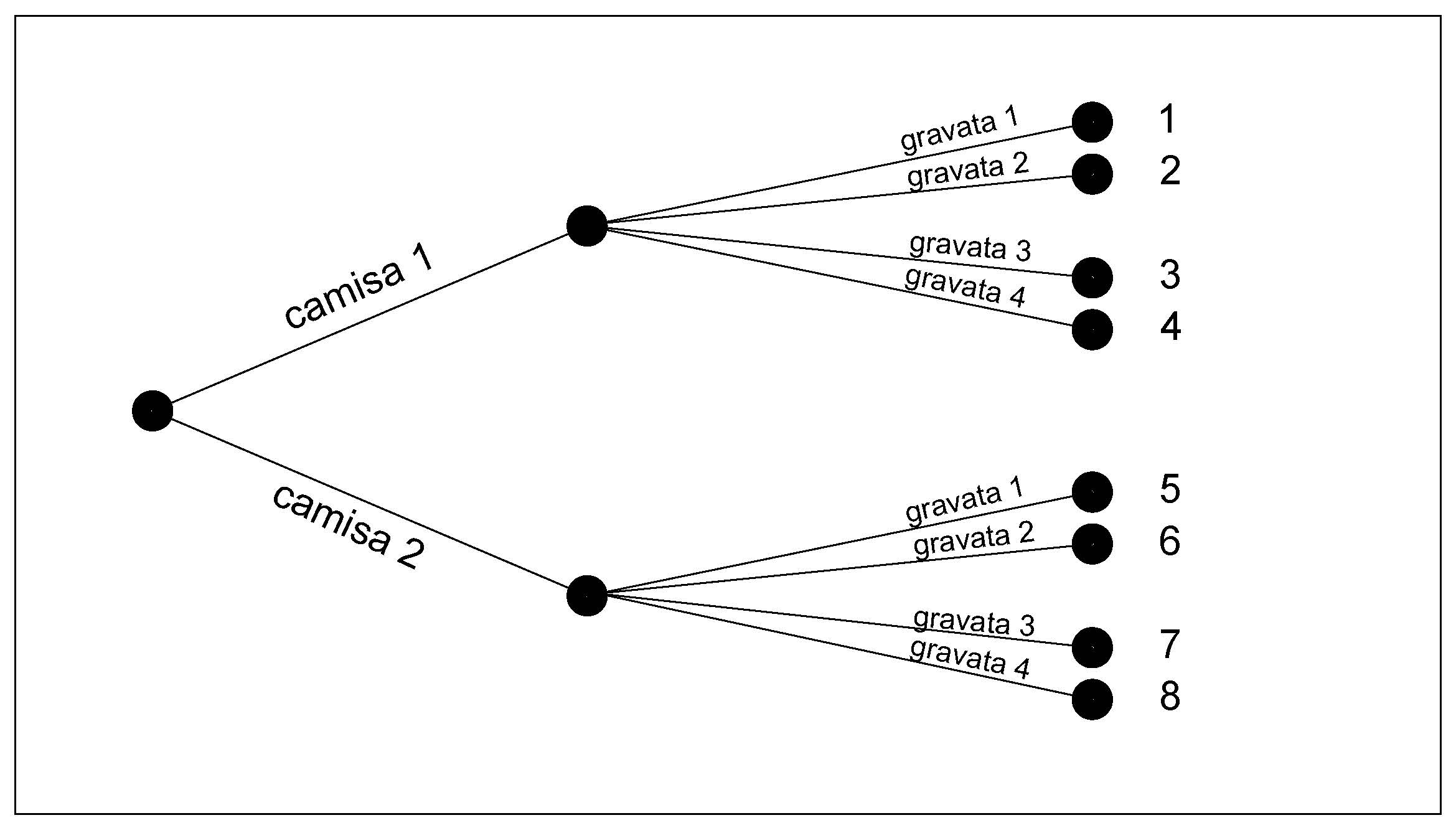
Figure 2.8: Diagrama de árvore

Ao lançarmos uma moeda três vezes (assumindo-se que K: cara e C: coroa) haverá \(2 \times 2 \times 2 = 8\) possibilidades distintas.

O diagrama de árvore associado será (cf. Figura 2.9:

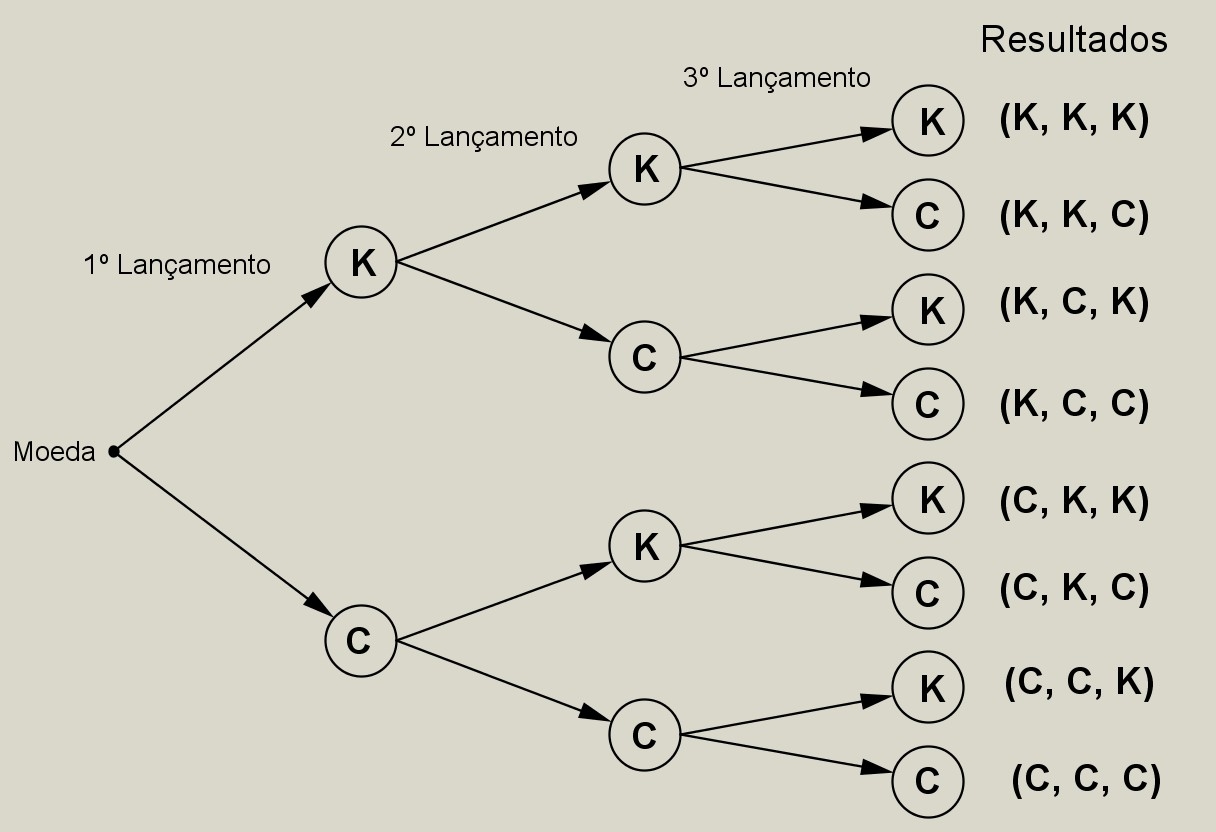
Figure 2.9: Diagrama de árvore

2.9.2 Regra da adição

Suponha agora os mesmos expermentos \(E\) e \(F\) que geram \(n\) e \(m\) resultados possíveis (\(E_{1},E_{2},E_{3}, \dots, E_{n}\) e \(F_{1},F_{2},F_{3}, \dots, F_{m}\)), mas que eeses experimentos não estejam mais alinhados sequencialmente: ocorre o evento \(E\) ou o evento \(F\). Então o número de maneiras pelas quais o evento \(E\) ou o evento \(F\) poderão se manifestar será de \(n + m\) maneiras diferentes:

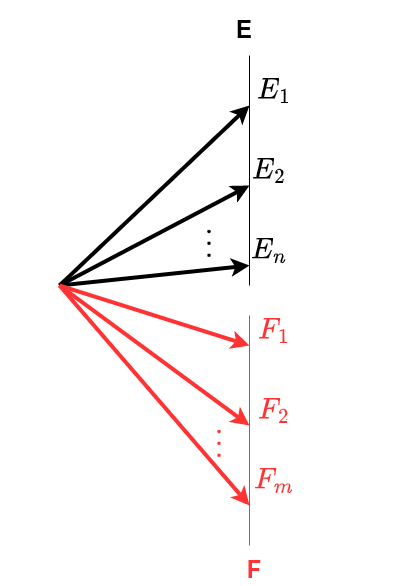
Figure 2.10: Regra da adição

Esse princípio recebe o nome de Princípio aditivo, e é aplicado nos casos em que os eventos são interligados pelo conectivo ou, característico de eventos mutuamente exclusivos: ocorre um ou outro.

Uma cantina de um colégio possui três tipos de sucos e dois tipos de refrigerantes. Um aluno pode adquirir apenas 1 suco ou 1 refrigerante. Quantas possibilidades de escolha ele tem?

Seja \(E_{1}\) definido como escolher um tipo de suco (\(n_{1}=3\)) e \(E_{2}\) definido como escolher 1 tipo de refrigerante (\(n_{2}=2\)). Então o número total de possíveis escolhas será dado aplicando-se o princípio aditivo:

\[ n_{1} + n_{2}=5 \]

2.9.3 Permutações (ordenação de elementos)

Suponha \(n\) objetos diferentes. Permutar os \(n\) objetos equivaleria a colocá-los dentro de uma caixa com \(n\) compartimentos em alguma ordenação.

O primeiro compartimento pode ser ocupado por qualquer um dos \(n\) objetos, o segundo por \(n-1\) e o último por apenas 1 objeto.

Assim, pelo princípio básico vemos que essa caixa poderá ser carregada de:

\[ n.(n-1).(n-2).1= n! \text{ maneiras diferentes.} \].

Exemplo: quantos diferentes arranjos ordenados das letras a, b e c são possíveis?

Pela enumeração direta vemos que são 6, ou seja, ‘abc’, ‘acb’, ‘bac’, ‘bca’, ‘cab’ e ‘cba’, resultado de \(3!=6\).

Exemplo: quantas diferentes ordens de rebatedores são possíveis em um time de beisebol formado por 9 jogadores?

\(9! = 362.880\) ordenamentos possíveis para os rebatedores.

Exemplo: uma turma de teoria da probabilidade é formada por 6 estudantes do sexo masculino e 4 do sexo feminino. Aplica-se uma prova e os estudantes são classificados de acordo com o seu desempenho. Suponha que nenhum dos estudantes tenha tirado a mesma nota. (a) Quantas diferentes classificações são possíveis? (b) Se os estudantes do sexo masculino forem classificados apenas entre si e também os do sexo feminino apenas entre si, quantas diferentes classificações são possíveis?

1. Como cada classificação corresponde a um arranjo particular das 10 pessoas, a resposta é \(10! = 3.628.800\).

2. Como há \(6!\) possíveis classificações dos homens entre si e \(4!\) classificações possíveis das mulheres entre si, segue do princípio básico que há \((6!)(4!)=(720)(24) = 17.280\) classificações possíveis neste caso.

2.9.4 Arranjos sem repetição

Considere um conjunto de \(n\) objetos diferentes. Suponha que desejamos selecionar uma quantidade \(p\) desses objetos, onde \(p < n\), e dispor os \(p\) objetos escolhidos em uma ordem específica.

Quando selecionamos e ordenamos um subconjunto de objetos de um conjunto maior, estamos formando arranjos ordenados. Nesse caso, o número total de arranjos possíveis de \(p\) elementos retirados de um conjunto de \(n\) objetos distintos (sem repetir nenhum elemento) é dado por:

\[ P_{(n,p)} = \frac{n!}{(n-p)!} \]

A fórmula para \(P_{(n,p)}\) considera tanto a seleção de \(p\) elementos quanto a ordenação deles, de modo que qualquer alteração na ordem dos elementos resulta em um novo arranjo.

Dessa forma, arranjos com os mesmos objetos em ordens distintas são considerados distintos.

Exemplo: quantos agrupamentos distintos, formados por 3 letras cada, podem ser formados com as 7 letras: A, B, C, D, E, F, G, considerando que não é permitido repetir nenhuma letra e que a ordem dos elementos importa?

\[\begin{align*} n & = 7 \\ p & = 3 \\ P_{(n,p)} & = \frac{7!}{ (7-3)!} \\ & = \frac{7!}{4!} = \\ & = \frac{ 7 \times 6 \times 5 \times 4! }{4!} \\ & = 7 \times 6 \times 5 = 210 \end{align*}\]

\(ABC, ACB, BAC, BCA, CAB, CBA, \dots\)

2.9.5 Arranjos com repetição

Considere um conjunto de \(n\) objetos diferentes. Suponha que desejamos selecionar uma quantidade \(p\) desses objetos, onde \(p < n\), e dispor os \(p\) objetos escolhidos em uma ordem específica.

Ao permitirmos a repetição dos objetos no agrupamento, cada posição pode ser ocupada por qualquer um dos \(n\) objetos, independentemente das escolhas anteriores.

Dessa forma, o número de arranjos com repetição de \(p\) elementos selecionados de um conjunto de nn objetos distintos é dado por:

\[ P_{(n,p)} = n ^{p} \]

Essa fórmula ocorre porque, ao preencher cada uma das \(p\) posições com qualquer um dos \(n\) objetos, multiplicamos \(n\) possibilidades para cada posição, resultando em:

\[ n \times n \times \ldots \times n = n^p \]

Exemplo: Quantos agrupamentos diferentes (onde a ordem dos elementos é razão para distinção: permutações) formados por 3 letras cada podem ser formados com as 7 letras: A, B, C, D, E, F, G com repetição?

\[\begin{align*} n & = 7 \\ p & = 3 \\ P_{(n,p)} & = n^{p} \\ & = 7 ^{3} = 343 \end{align*}\]

Primeira posição: temos 7 opções (uma das 7 letras). Segunda posição: também temos 7 opções, pois a repetição é permitida. Terceira posição: novamente, temos 7 opções.

\(AAA, AAB, AAC, \dots\)

2.9.6 Combinações sem repetição

Em uma permutação, a ordem dos objetos em cada agrupamento é essencial: qualquer alteração na ordem cria um agrupamento distinto. Por exemplo, o agrupamento abc é diferente de bca numa permutação, pois a ordem importa.

Em muitos problemas, entretanto, estamos interessados somente na seleção dos objetos, sem considerar a ordem em que eles aparecem.

Nesse caso, os agrupamentos onde os mesmos elementos aparecem em ordens diferentes são considerados equivalentes. Tais seleções são chamadas de combinações. Por exemplo, abc e bca representam uma mesma combinação, pois contêm os mesmos elementos independentemente da ordem.

O conceito de uma combinação refere-se a um conjunto de \(n\) objetos distintos, dos quais escolhemos \(p\) objetos \((p < n)\) sem repetição. Assim:

• a ordem não importa: então \(abc\) é igual a \(bca\) (os agrupamentos que contêm os mesmos objetos em qualquer ordem são considerados iguais);
• a repetição não permitida: cada objeto só aparece uma vez em cada agrupamento.

O número total de combinações possíveis de \(p\) objetos selecionados de um conjunto de \(n\) objetos distintos é dado por:

\[ C_{(n,p)} = \frac{n!}{p! \times (n-p)!} \]

em que o numerador (\(n!\)) representa o número total de maneiras de permutar todos os \(n\) objetos, o denominador (\(p! \times (n - p)!\)) remove as redundâncias causadas pela permutação dos \(p\) objetos escolhidos (\(p!\)) e das maneiras de ordenar os \((n - p)\) objetos restantes (\((n - p)!\)).

A fórmula resulta no número de agrupamentos únicos onde apenas a composição do conjunto importa, e a ordem dos elementos dentro de cada conjunto não afeta a contagem.

Exemplo: Qual é número de formas nas quais \(3\) cartas podem ser escolhidas ou selecionadas de um total de \(8\) cartas diferentes?

\[\begin{align*} n & = 8 \\ p & = 3 \\ C_{(n,p)} & = \frac{n!}{p! \times (n - p)!}\\ C_{(8,3)} & = \frac{8!}{ 3! (8-3)!} \\ & = \frac{8!}{3! \times 5!} \\ & = \frac{ 8 \times 7 \times 6 \times 5! }{ 3! \times 5! } \\ & = \frac{ 8 \times 7 \times 6 }{3!} = 56 \end{align*}\]

O número total de combinações com repetição, de \(p\) objetos selecionados de \(n\) (também chamado de combinações de \(n\) elementos tomados \(p\) a cada vez com repetição) é representado por:

\[ C_{(n+p-1,p)} = \frac{ (n+p-1)! }{ p! \times ( n-1)!} \]

Exemplo: um comitê de três pessoas deve ser formado a partir de um grupo de 20 pessoas. Quantos comitês diferentes são possíveis?

\[\begin{align*} n & = 20 \\ p & = 3 \\ C_{(n,p)} & = \frac{n!}{p! \times (n - p)!}\\ C_{(20,3)} & = \frac{20!}{3! \times (20 - 3)!}\\ & = \frac{20 \times 19 \times 18 \times 17!}{3! \times 17!}\\ & = \frac{20 \times 19 \times 18}{3 \times 2 \times 1}\\ & = \frac{6840}{6} = 1140 \end{align*}\]

Exemplo: de um grupo de cinco mulheres e sete homens, quantos comitês diferentes formados por duas mulheres e três homens podem ser formados? E se dois dos homens estiverem brigados e se recusarem a trabalhar juntos?

Para resolver esse problema, vamos dividi-lo em duas partes:

1. calcular o número de comitês possíveis formados por duas mulheres e três homens (combinações \(C_{(5,2})\) e \(C_{(7,3})\))
2. Calcular o número de comitês possíveis se dois dos homens estiverem brigados e se recusarem a trabalhar juntos.

Parte 1: Comitês sem restrição

Escolha das Mulheres: Temos 5 mulheres e precisamos escolher 2. O número de maneiras de fazer isso é uma combinação, dada por:

\[ C_{(5, 2)} = \frac{5!}{2! \times (5 - 2)!} = \frac{5 \times 4}{2 \times 1} = 10 \]

Escolha dos Homens: Temos 7 homens e precisamos escolher 3. O número de maneiras de fazer isso também é uma combinação, dada por:

\[ C_{(7, 3)} = \frac{7!}{3! \times (7 - 3)!} = \frac{7 \times 6 \times 5}{3 \times 2 \times 1} = 35 \]

O número total de comitês é o produto das duas combinações (princípio básico):

\[ \text{Total} = C_{(5, 2)} \times C_{(7, 3)} = 10 \times 35 = 350 \]

Portanto, sem restrições, há 350 comitês diferentes que podem ser formados.

Parte 2: Comitês com restrição (Dois Homens Brigados)

Para calcular o número de comitês possíveis com essa restrição, usamos o princípio da exclusão: (total de comitês sem restrição - total de comitês com restrição). Começamos contando quantos comitês incluem os dois homens brigados: \(A\) e \(B\).

Se ambos estão no comitê então precisamos escolher apenas mais 1 homem entre os 5 homens restantes. O número de maneiras de fazer isso é:

\[ C_{(5, 1)} = 5 \]

Então, do total de 35 possíveis grupos de 3 homens formados sem restrição apenas 5 são grupos onde \(A\) e \(B\) estão presentes, resultando então em \(35-5=30\) grupos onde \(A\) e \(B\) estão ausentes.

Compondo com o número de possíveis grupos de mulheres (princípio básico) teremos:

\[ \text{Total} = C_{(5, 2)} \times30 = 10 \times 30 = 300 \]

Portanto, com essa restriçãose, há 300 comitês diferentes que podem ser formados.

2.9.7 Combinações com Repetição

Em muitos problemas de contagem, estamos interessados em selecionar um subconjunto de objetos de um conjunto maior, sem nos preocupar com a ordem dos objetos. Isso é chamado de combinação. No entanto, ao contrário das combinações convencionais, em alguns casos é permitido que os mesmos objetos sejam escolhidos mais de uma vez. Essas são conhecidas como combinações com repetição.

Nas combinações com repetição, selecionamos \(p\) objetos a partir de um conjunto de \(n\) objetos distintos, permitindo que cada objeto seja escolhido mais de uma vez. Nesse contexto: a ordem dos objetos não importa, ou seja, uma seleção de A,B,A é considerada igual a A,A,B e a repetição é permitida, então podemos escolher o mesmo objeto mais de uma vez.

Combinações com repetição são úteis em contextos onde é necessário selecionar subconjuntos com elementos repetidos, como: - escolha de itens com reposição (como selecionar moedas em valores específicos). - problemas de contagem em álgebra combinatória. - distribuição de recursos em cenários onde itens podem ser alocados mais de uma vez.

O número de combinações com repetição para selecionar \(p\) objetos de um conjunto de \(n\) objetos distintos é dado por:

\[ C_{(n + p - 1, p)} = \frac{(n + p - 1)!}{p! \times (n - 1)!} \]

Essa fórmula reflete o fato de que, ao permitir repetições, cada seleção possível pode ser visualizada como uma combinação com um conjunto “expandido” de opções, onde as escolhas de um mesmo objeto múltiplas vezes são válidas e contadas.

Exemplo: quantas maneiras existem de selecionar 3 frutas de um conjunto com 5 tipos diferentes (maçã, banana, laranja, uva e pera), onde repetições são permitidas?

\[\begin{align*} n & = 5 \\ p & = 3 \\ C_{(n + p - 1, p)} & = \frac{(n + p - 1)!}{p! \times (n - 1)!}\\ C_{(5 + 3 - 1, 3)} & = \frac{(5 + 3 - 1)!}{3! \times (5 - 1)!} = \frac{7!}{3! \times 4!}\\ & = \frac{7 \times 6 \times 5 \times 4!}{3! \times 4!} = \frac{7 \times 6 \times 5}{3 \times 2 \times 1} = \frac{210}{6} = 35 \end{align*}\]

Exemplo: supondo que você queira comprar um sorvete com 4 bolas em uma sorveteria que possui 3 sabores disponíveis: chocolate, baunilha e morango. De quantos modos diferentes você pode fazer esta compra? (Note que nesta combinação é possível repetir a ordem de dois ou mais sabores, assim tratando de uma combinação com repetição).

\[\begin{align*} n & = 3 \\ p & = 4 \\ C_{(n + p - 1, p)} & = \frac{(n + p - 1)!}{p! \times (n - 1)!}\\ C_{(n+p-1,p)} & = \frac{(3+4-1)!}{ 4! (3-1)!} = 15 \end{align*}\]