4.2 Conceitos essenciais
4.2.1 Experimentos determinísticos e experimentos aleatórios
Aleatório provem do latim: aleatorium: fato cujo desfecho depende de um acontecimento futuro e incerto, resultado da sorte ou acaso, acidental.
Probabilidade deriva do latim: probabilitas: qualidade do que se pode comprovar, de probabilis: o que pode passar por um teste, provável e de probare: provar, testar, examinar.
Ao contrário de um experimento determinístico, cujo resultado pode ser previamente determinado como :
- como a reação de dois átomos de hidrogênio com um átomo de oxigênio: \(2H_{2}+O_{2} \to 2H_{2}O\) e
- a distância \(S\) percorrida no vácuo sob velocidade constante \(V\) e sem atrito num intervalo de tempo \(t\): \(S = V \times t\)
o conceito de experimento aleatório é o que estabelece que seu resultado não pode ser previsto com certeza como em:
- o lançamento de um dado. O resultado pode ser qualquer número inteiro de 1 a 6 e
- a medição da altura de uma pessoa selecionada aleatoriamente.
Os resultados observados apresentam variações mesmo quando esses experimentos são repetidos indefinidamente e sob as mesmas condições; todavia, é possível estabelecer um conjunto cujos elementos compõem todos os possíveis resultados:
- qualquer número inteiro de 1 a 6: e o conjunto de possíveis resultados é finito e
- qualquer valor em um intervalo contínuo por exemplo, entre 1,50 m e 2,00 m (com infinitas possibilidades dentro desse intervalo).
4.2.2 O espaço amostral
A primeira coisa que fazemos quando começamos a pensar sobre a probabilidade de ocorrência de um certo resultado em um experimento aleatório é tentar listar todos os resultados com possibilidade de ocorrência.
Esses resultados formam um conjunto a que denominamos de espaço amostral que, usualmente, é representado pela letra grega maiúscula \(\Omega\).
Para que \(\Omega\) seja considerado o espaço amostral desse experimento aleatório ele precisa apresentar duas propriedades:
- apenas um de seus elementos ocorre cada vez que realizamos o experimento aleatório; e,
- pelo menos um dos possíveis resultados ocorre sempre que realizarmos o experimento aleatório.
Essas condições indicam que os elementos de \(\Omega\) são mutuamente exclusivos e exaustivos.
4.2.2.1 Espaços aleatórios discretos
- são finitos ou contáveis (infinito numerável)
- pode-se atribuir uma probabilidade para cada resultado
Exemplo 1:
- Experimento aleatório: lançar um dado e contar o número de pontos na face que ficar exposta para cima
- Espaço amostral finito: \(\Omega = \{1,2,3,4,5,6\}\)
Exemplo 2:
- Experimento aleatório: lançar dois dados e contar o número de pontos nas faces que ficarem expostas para cima
- Espaço amostral finito: \(\Omega = \{2,3,4,5,6,7,8,9,10,11,12\}\)
Exemplo 3:
- Experimento aleatório: lançar uma moeda e contar o número de lançamentos necessários até se obter uma “cara”
- Espaço amostral infinito contável: \(\Omega = \{1,2,3,4,5, \dots, k, \dots\}\)
Exemplo 4:
- Experimento aleatório: lançar um dado até se obter um “6”
- Espaço amostral infinito contável: \(\Omega = \{1,2,3,4,5, \dots, k, \dots\}\)
Um espaço amostral consiste então da enumeração (finita ou infinita contável) de todos os possíveis resultados de serem obtidos em um experimento aleatório.
Cada um dos possíveis resultados de um experimento aleatório é chamado de um elemento desse espaço amostral. Assim, para o espaço amostral \(\Omega\), seus elementos serão representados por letras gregas minúsculas \(\omega_{n}\)
\[ \Omega = \{\omega_{1}, \omega_{2}, \omega_{3}, ..., \omega_{n}, \dots \} \]
4.2.2.2 “Espaços” aleatórios contínuos
- não são contáveis: os resultados possíveis formam um intervalo contínuo de valores
- probabilidade de um resultado específico é zero: como existem infinitos resultados possíveis, a probabilidade de um valor específico é 0
- probabilidades são atribuídas a intervalos: a probabilidade de um evento é associada à extensão do intervalo (comprimento, área, volume, etc.) que o evento ocupa.
Exemplo 1:
- Experimento aleatório: a altura de uma pessoa aleatoriamente sorteada
- Intervalo amostral: \(\Omega = [1,5 ; 2,0 ]\) m
Exemplo 2:
- Experimento aleatório: o peso de uma pessoa aleatoriamente sorteada
- Intervalo amostral: \(\Omega = [10 ; 100 ]\) kg
Exemplo 3:
- Experimento aleatório: o teor de um minério por quuilo de uma amostra de solo extraída de um local aleatório
- Intervalo amostral: \(\Omega = [0,001 ; 0,01]\) gramas
4.2.2.3 Espaços amostrais equiprováveis e não equiprováveis
Se todos os elementos que compõem um espaço amostral finito de um experimento aleatório possuem a mesma probabilidade de ocorrência é dito que o espaço amostral desse experimento aleatório é equiprovável (com a mesma probabilidade para todos os seus elementos).
Exemplo 1
- Experimento aleatório: lançar um dado e contar o número de pontos na face que ficar exposta para cima
- Espaço amostral finito: \(\Omega = \{1,2,3,4,5,6\}\)
- Probabilidades: \(P(1)=\frac{1}{6},P(2)=\frac{1}{6},\\P(3)=\frac{1}{6},P(4)=\frac{1}{6},\\P(5)=\frac{1}{6},P(6)=\frac{1}{6}\)
> Exemplo 2
- Experimento aleatório: lançar dois dados e contar o número de pontos nas faces que ficarem expostas para cima
- Espaço amostral finito: \(\Omega = \{2,3,4,5,6,7,8,9,10,11,12\}\)
- Probabilidades: \(P(2)=\frac{1}{36},P(3)=\frac{2}{36},P(4)=\frac{3}{36},P(5)=\frac{4}{36},\\P(6)=\frac{5}{36},P(7)=\frac{6}{36}, P(8)=\frac{5}{36}, P(9)=\frac{4}{36},\\ P(10)=\frac{3}{36}, P(11)=\frac{2}{36}, P(12)=\frac{1}{36}\)
Cada um dos elementos que compõem o espaço amostral (a soma dos valores numéricos das faces no lançamento de um dado por duas vezes) poderá resultar de diferentes combinações de valores.
A Tabela 4.1 apresenta todas as combinações possíveis de serem obtidas, bem como as proporções em relação ao total para cada elemento do espaço amostral.
| Soma | Possíveis combinações de resultados nos lançamentos | Frequência \(n_{i}\) | Proporção \(f_{i}\) |
|---|---|---|---|
| (primeiro,segundo) | |||
| 2 | (1,1) | 1 | \(\frac{1}{36}\) |
| 3 | (1,2); (2,1) | 2 | \(\frac{2}{36}\) |
| 4 | (1,3); (2,2); (3,1) | 3 | \(\frac{3}{36}\) |
| 5 | (1,4); (2,3); (3,2); (4,1) | 4 | \(\frac{4}{36}\) |
| 6 | (1,5); (2,4); (3,3); (4,2); (5,1) | 5 | \(\frac{5}{36}\) |
| 7 | (1,6); (2,5); (3,4); (4,3); (5,2); (6,1) | 6 | \(\frac{6}{36}\) |
| 8 | (2,6); (3,5); (4,4); (5,3); (6,2) | 5 | \(\frac{5}{36}\) |
| 9 | (3,6); (4,5); (5,4); (6,3) | 4 | \(\frac{4}{36}\) |
| 10 | (4,6); (5,5); (6,4) | 3 | \(\frac{3}{36}\) |
| 11 | (5,6); (6, 5) | 2 | \(\frac{2}{36}\) |
| 12 | (6,6) | 1 | \(\frac{1}{36}\) |
| Totais | 36 | \(1\) |
As probabilidades de ocorrência de cada um os elementos desse espaço amostral são diferentes e, por essa razão é dito que o espaço amostral desse experimento aleatório tem elementos não equiprováveis.
4.2.3 Evento
Define-se como evento de interesse um subconjunto finito do espaço amostral, composto por um ou mais de seus elementos que satisfazem o enunciado estabelecido no experimento aleatório proposto.
A expressão evento de interesse (também chamado de sucesso) refere-se, no contexto do cálculo de probabilidades, à ocorrência de um resultado desejado durante a realização de um experimento aleatório.
Frequentemente, eventos de interesse são representados por letras maiúsculas do alfabeto romano e podem ser acompanhados de uma notação explicativa, como \(E(\dots)\).
Por exemplo, considere um experimento aleatório que consiste em lançar um dado uma única vez. Um possível evento de interesse pode ser: E(obtenção do número 2) (\(E(2)\)) e, nesse contexto pode ser a obtenção do número 2 como resultado.
Podemos ter variados tipos de eventos de interesse como:
- simples ou compostos;
- certos ou impossíveis;
- dependentes ou independentes ;
- mutuamente exclusivos ;
- complementares;
4.2.3.1 Diagramas de Venn para representar o espaço amostral e eventos de interesse
Em muitos dos problemas de probabilidade, o evento de interesse pode se definido como associações de dois ou mais eventos formados, por sua vez, por um ou mais elementos do espaço amostral do experimento aleatório. Uniões, interseções e complementos são algumas dessas associações que, doravante, serão muito utilizados.
Por essa razão, a representação do espaço amostral e esses eventos por meio de Diagramas de Venn pode ajudar a compreensão de um problema de cálculo probabilidade.

Figure 4.2: John Venn, 1834–1923
4.2.3.1.1 União \(A \cup B\)
Sejam \(A\) e \(B\) dois eventos de interesse definidos sobre o espaço amostral \(\Omega=\{1,2,3,4,5,6\}\) (lançamento de um dado) tais que \(A=\{1,2,3\}\) e \(B=\{2,4,6\}\).
Um evento de interesse \(E\) expresso como a união desses dois outros, representado por \(E=(A \cup B)\), será o subconjunto do espaço amostral \(\Omega\) que contém os elementos que pertençam a \(A\), ou a \(B\) ou a ambos.
Desse modo, \(E=A \cup B=\{1,2,3,4,6\}\) e o Diagrama de Venn correspondente será:
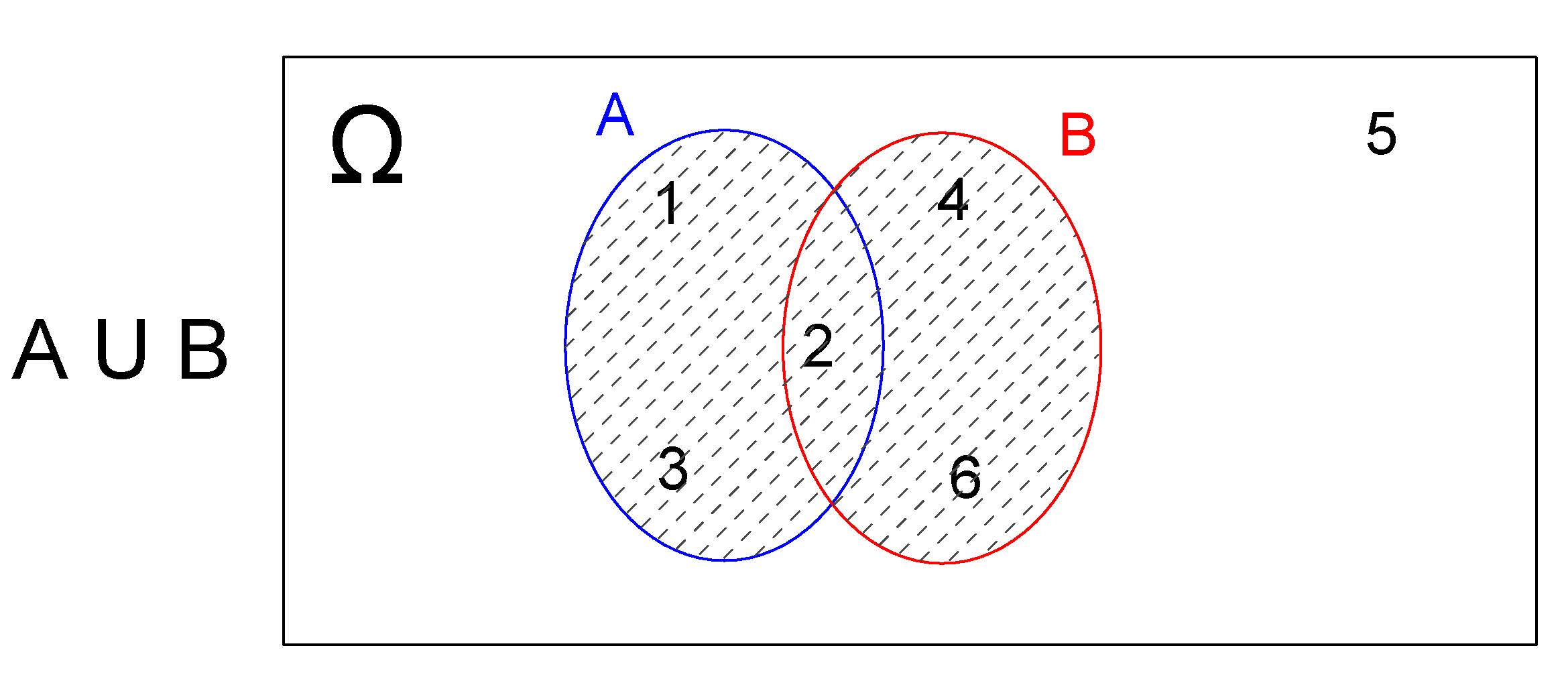
Figure 4.3: União: \(A \cup B\)
Na realização desse experimento aleatório (lançar um dado) o evento de ineteresse \(E\) ocorrerá quando qualquer um dos resultados for um elemento pertencente a \(A\), ou a \(B\) ou a ambos.
4.2.3.1.2 Interseção \(A \cap B\)
Um evento de interresse \(E\) definido como a interseção dos eventos \(A\) e \(B\) anteriormente definodos, representado por \(E=(A \cap B)\), será o subconjunto do espaço amostral \(\Omega\) que contém todos os elementos que pertençam a ambos os eventos A e B simultaneamente.
Desse modo, \(E=(A \cap B) =\{2\}\) e o Diagrama de Venn correspondente será:
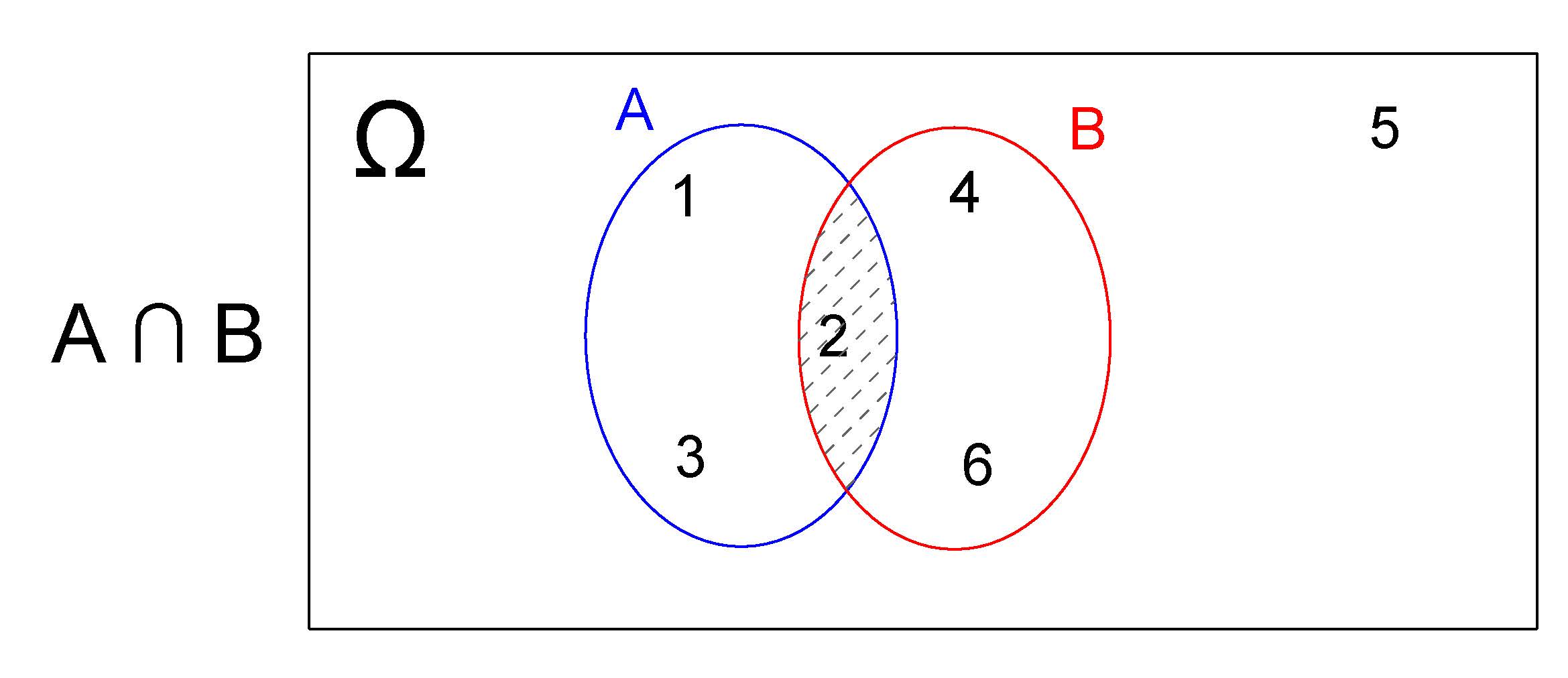
Figure 4.4: Interseção: \(A \cap B\)
Na realização desse experimento aleatório (lançar um dado) o evento de interesse \(E\) ocorrerá apenas quando o resultado for um elemento simultaneamente pertencente a \(A\) e \(B\) .
Quando o evento de interesse é definido pela interseção de dois outros, todavia esssa interseção é vazia, representa-se \(E\) como
\[ E(A \cap B) = \varnothing \]
4.2.3.1.3 Complemmento \(A^{c}\)
Um evento de intersse pode também ser definido como o complemento de outros como, por exemplo, de \(A\), sendo representado representado por \(E=(A^{c})\) (ou \(E=(\stackrel{-}{A})\)).
Desse modo, \(E=(A^{c}) =\{4,5,6\}\) e o Diagrama de Venn correspondente será:
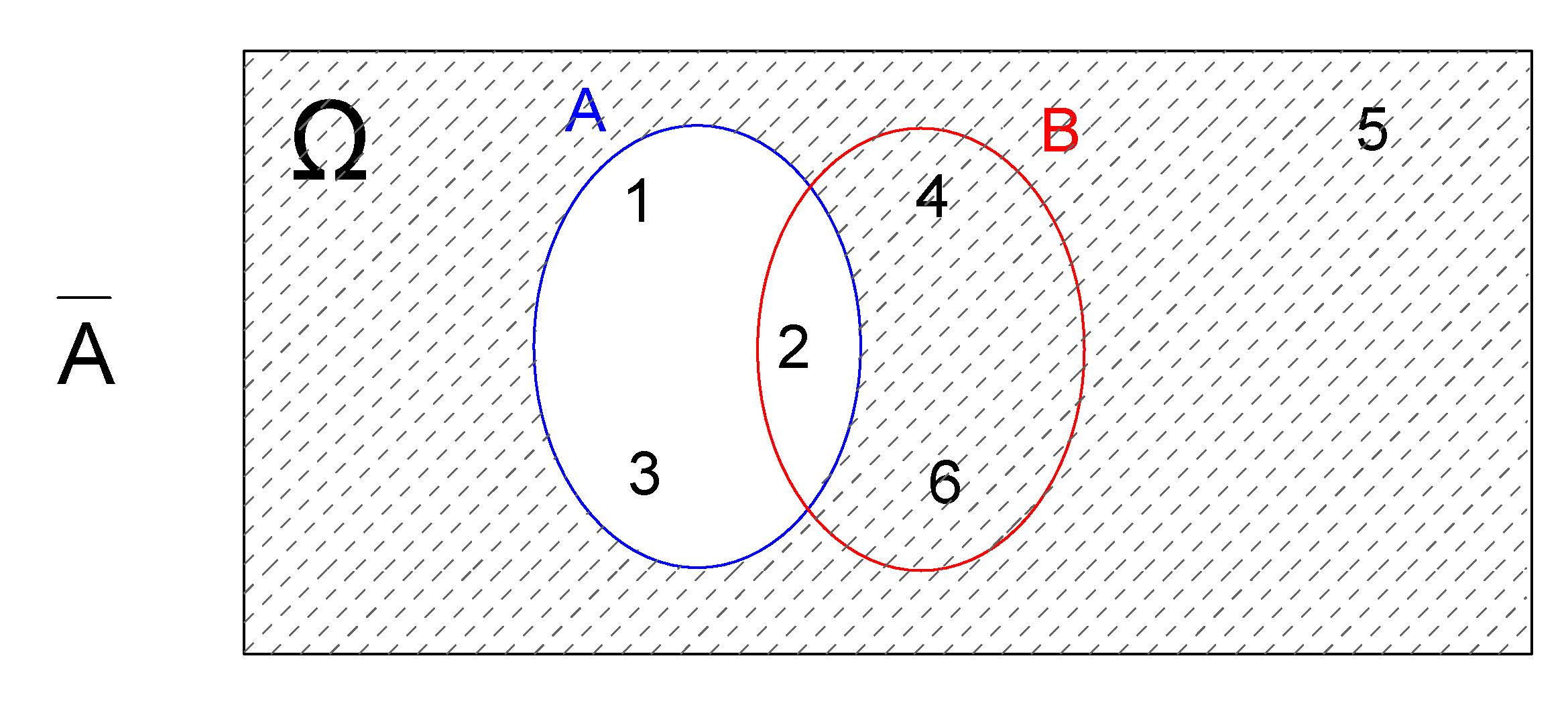
Figure 4.5: Complementar \(A^{c}\)
De modo análogo, para \(E=(B^{c})=\{1,3,5\}\) e o Diagrama de Venn correspondente será :
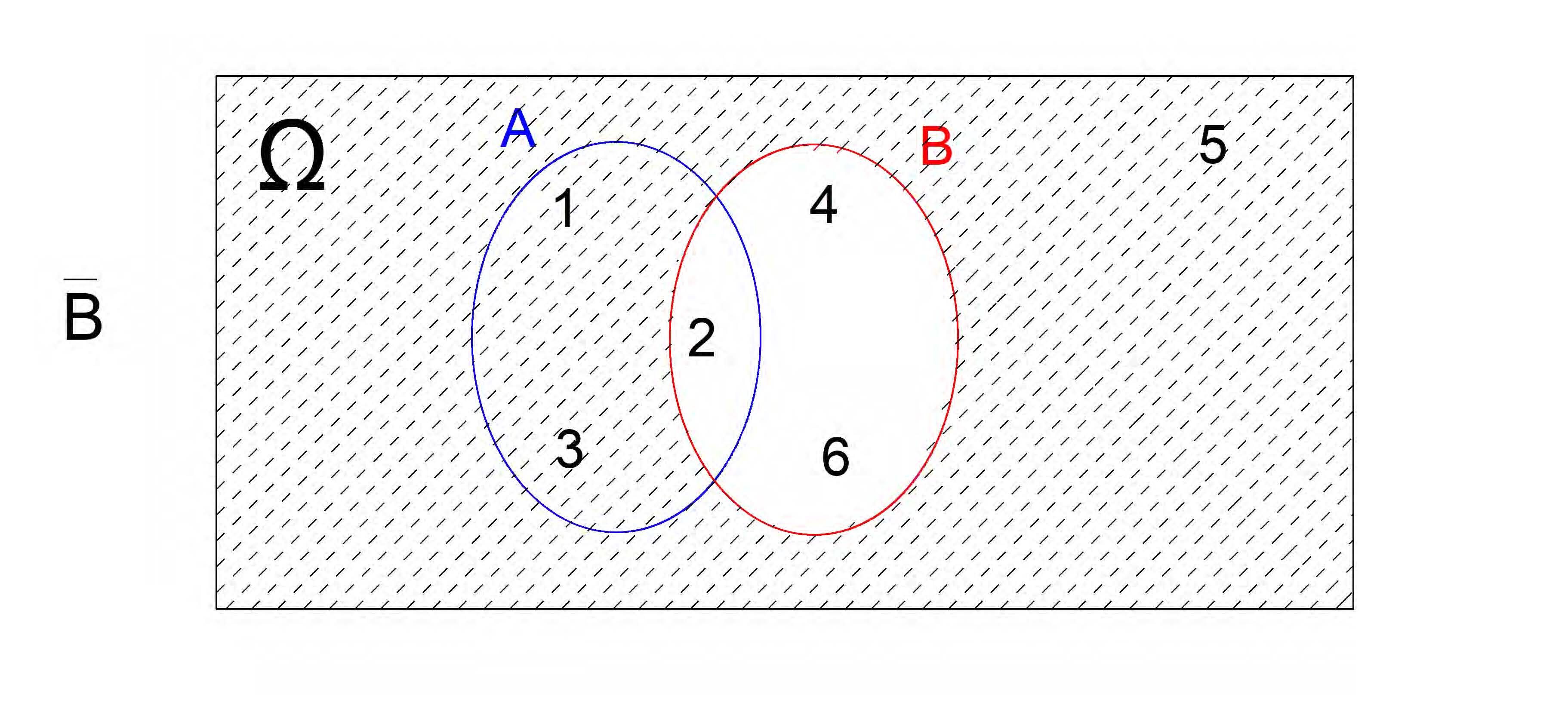
Figure 4.6: Complementar de B
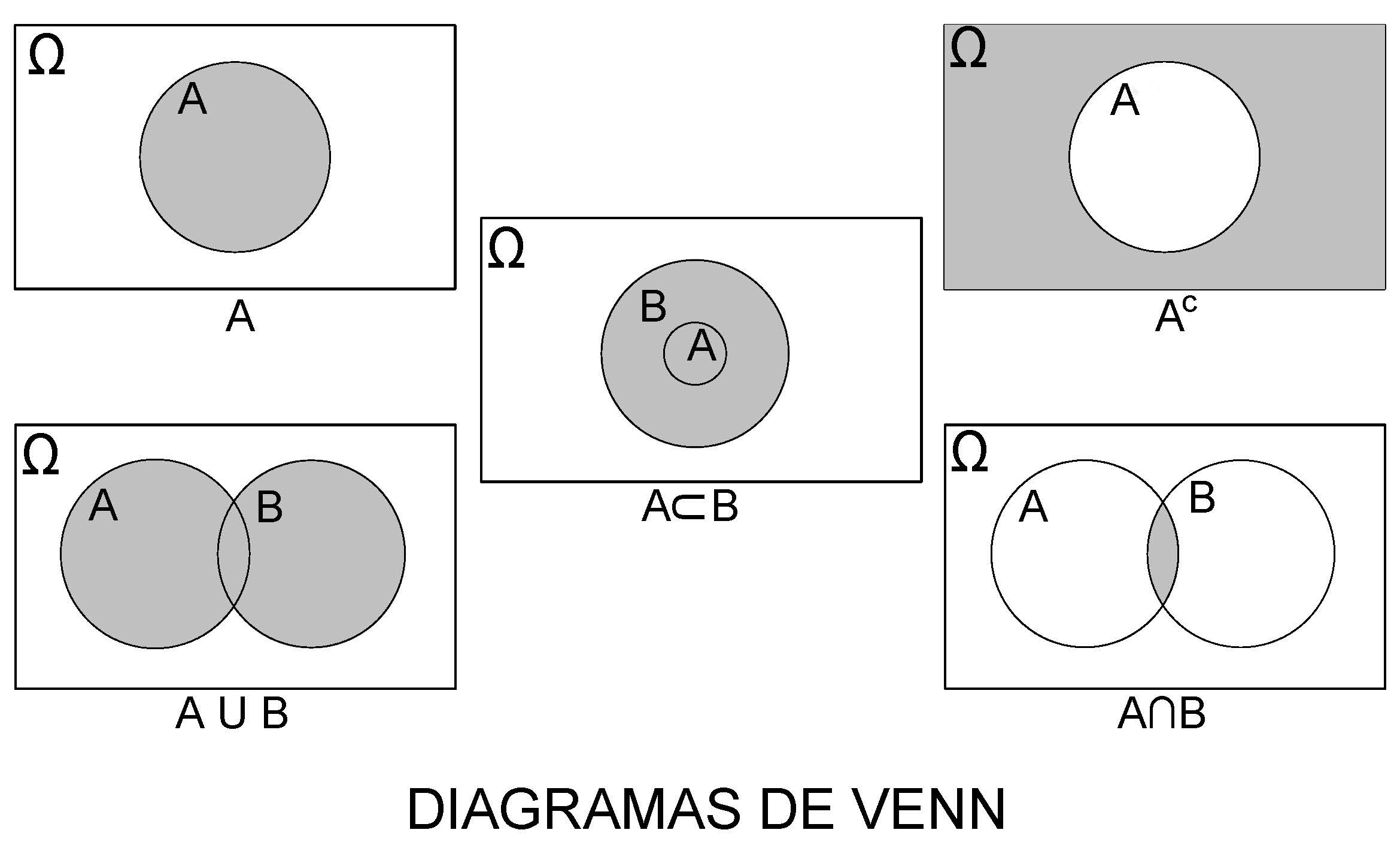
Figure 4.7: Diagramas de Venn
4.2.3.2 Eventos simples e eventos compostos
O evento de interesse (\(E(2)\)) definido no experimento aleatório anterior (obter o número 2) é formado por apenas um elemento do espaço amostral. Eventos formados por apenas um elemento do espaço amostral são denominados de evento simples.
\[
\Omega = \{1; 2; 3; 4; 5; 6\}\\
E(2) = \{2\}
\]
Admita agora o mesmo experimento aleatório todavia definindo como evento de interesse (Eobter-se um número par. Um evento de interesse assim definido é um evento composto uma vez que é formado por mais de um elemento do espaço amostral:
\[ \Omega = \{1; 2; 3; 4; 5; 6\}\\ E(par) = \{2; 4; 6\} \]
Outro exemplo, a partir de um experimento aleatótrio que consiste em se lançar uma moeda duas vezes, cujo espaço amostral é representado por um conjunto composto por quatro elementos
\[ \Omega = \{(\text{Cara}, \text{Coroa}),(\text{Coroa}, \text{Cara}),(\text{Cara}, \text{Cara}), (\text{Coroa}, \text{Coroa})\} \]
Se definirmos como evento de interesse na realização desse experimento aleatório obter-se \(E=\{(Cara, Cara)\}\), o evento \(E\) será um evento simples pois é formado por apenas um elemento do espaço amostral.
Se, por outro lado, definimos como sucesso obter-se \(E_{1}=\{(Cara, Coroa) \text{ ou } (Coroa, Cara)\}\), o evento \(E_{1}\) será um evento composto pois é formado por dois elementos do espaço amostral.
Se codificarmos Cara=1 e Coroa=0, podemos representar num plano \(XY\) o espaço amostral \(\Omega\) desse experimento aleatório e o evento de sucesso \(E_{1}\)
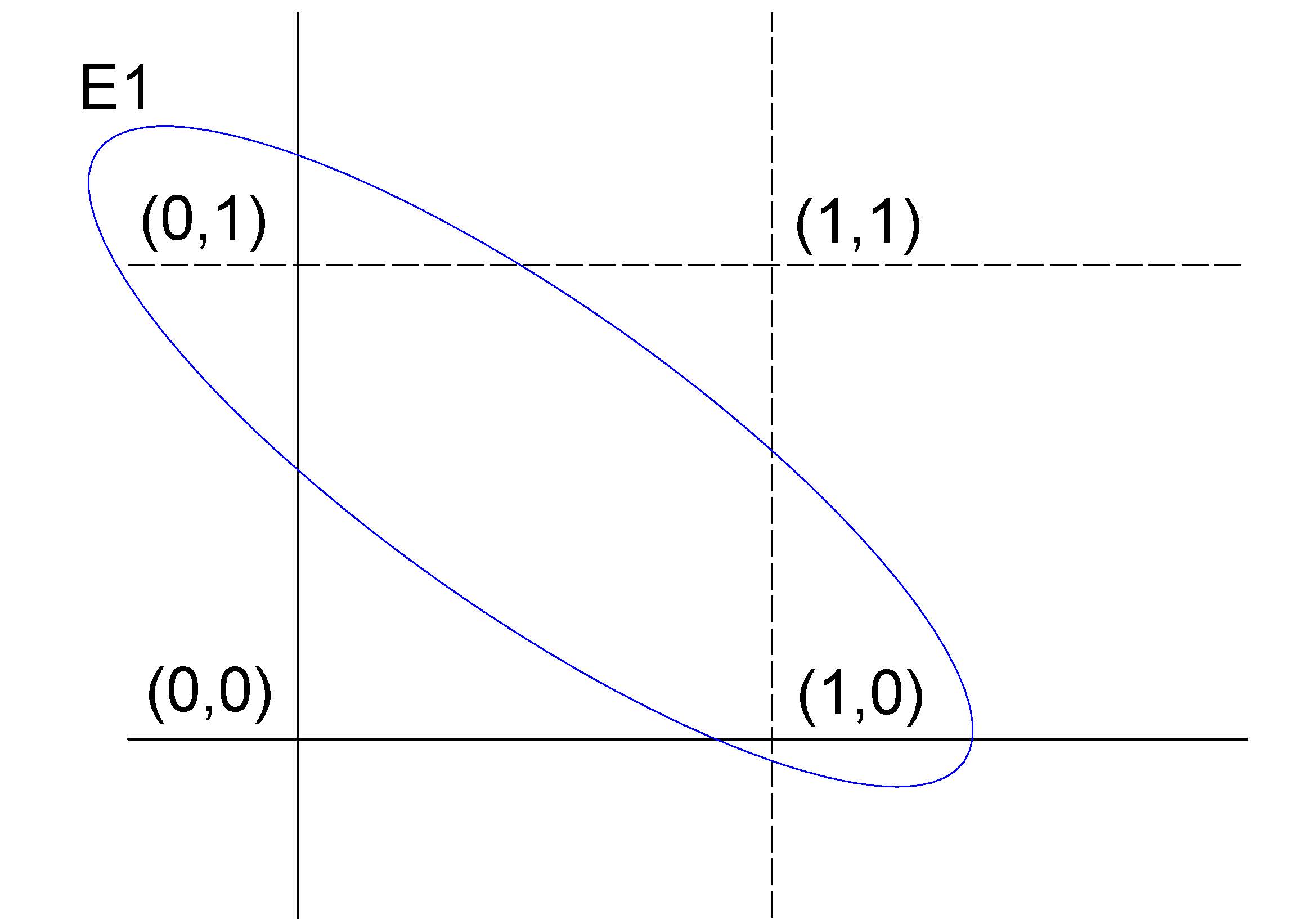
Figure 4.8: Representação gráfico do espaço amostral do experimento aleatório e do evento de interesse definido
4.2.3.3 Eventos certos e eventos impossíveis
Um evento de interesse \(G\), definido sobre o espaço amostral \(\Omega\), em que \(G = \Omega\), expressa que qualquer elemento de \(\Omega\) satisfaz o evento \(G\), ou seja, qualquer um dos possíveis resultados do experimento aleatório corresponde ao evento.
Um evento de interesse assim definido ocorrerá com certeza, razão pela qual tais eventos são denominados eventos certos.
Por outro lado, se definirmos um evento de interesse \(I\) que não contém resultados pertencentes a \(\Omega\) — o espaço amostral, ou seja, todos os resultados possíveis — como, por exemplo, obter o número 7 no lançamento de um dado de seis faces, esse evento será impossível de ocorrer.
Eventos assim definidos são chamados de eventos impossíveis.
4.2.3.4 Eventos independentes
Dois eventos são considerados independentes quando a probabilidade de ocorrência de um evento de interesse em um determinado experimento aleatório não é influenciada pelo resultado prévio de outro evento.
Em outras palavras, a ocorrência de um evento não altera a probabilidade do outro. Caso contrário, esses eventos são classificados como dependentes ou condicionados.
Este conceito será explorado em maior detalhe em seções posteriores.
4.2.3.5 Eventos mutuamente exclusivos
Dois eventos que nunca poderão ocorrer simultaneamente são ditos mutuamente exclusivos. No experimento do lançamento da moeda por uma vez, nunca observaremos, simultaneamente, dois eventos como \(E=\{(Cara)\}\) e \(F=\{(Coroa)\}\).
Um evento assim definido teria sua interseção vazia
\[ G=(E \cap F) = \varnothing \]
e, por essa razão, sua probabilidade será \(P(G)=P(E \cap F)=0\).
4.2.3.6 Eventos complementares
Definido um evento de interesse qualquer pode-se observar apenas dois resultados:
- ocorrer;
- não ocorrer o sucesso.
Ou seja, um ou outro deverá forçosamente ocorrer.
Chama-se de evento complementar (\(E^{c}\) ou \(\stackrel{-}{E}\)) a um evento (\(E\)) e sua probabilidade de sucesso será:
\[ P(E^{c}) = 1 - P(E) \]
Se a probabilidade de sucesso de que ele ocorra for \(P(E)=p\) e a de que ele não ocorra for \(P(E^{c}= q)\) vê-se que a soma dessas quantidades deverá ser \(p + q =1\), novamente antecipando um dos postulados do conceito axiomático de probabilidade.
4.2.4 Probabilidade
4.2.4.1 Conceito clássico ou a priori
Sob uma visão intuitiva, a probabilidade como uma medida da informação que temos sobre a possibilidade de ocorrência de um evento aleatório, pode ser definida como a medida numérica expressa em termos relativos (percentuais), obtida pela razão (proporção) entre o número de eventos favoráveis (sucessos) pelo número total de eventos prováveis no experimento (espaço amostral).
Esse conceito de probabilidade é denominado clássico ou a priori, baseado em um conhecimento prévio ou uma crença subjetiva sobre a probabilidade de um evento ocorrer.
Por exemplo, um jogador de cartas pode ter uma crença a priori de que a probabilidade de uma carta ser um ás é de 1 em 13, independentemente do número de baralhos no jogo
A distribuição de frequências é um instrumento importante para a análise da variabilidade de experimentos aleatórios e, em particular, as frequências relativas são estimativas das probabilidades.
\[ P(E)= \frac{\text{número de resultados de interesse (sucessos)}}{\text{número total de resultados possíveis no espaço amostral}} \]
Com o estabelecimento de suposições adequadas, um modelo teórico de probabilidade pode ser empregado sem a realização a priori do experimento aleatório, reproduzindo de modo razoável a distribuição das frequências quando o experimento é realizado.
Consideremos o exemplo do experimento que consiste em se lançar um dado e observar o valor numérico de sua face. As suposições que deveriam ser estabelecidas a priori são:
- só pode ocorrer uma das seis faces; e,
- o dado utilizado não possui viés algum (não favorece face alguma).
Como todos os \(N\) resultados do espaço amostral apresentam uma mesma probabilidade de ocorrência, então a proporção teórica de ocorrência de qualquer um desse resultados poderá ser apresentado na forma vista na na forma vista na Tabela 4.2.
\[ P(E)= \frac{1}{N} \]
| Face | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|---|---|---|---|---|---|---|
| Proporção teórica | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | 1 |
Sendo equiprováveis todos os elementos do espaço amostral, todos terão a mesma probabilidade de ocorrência que será:
\[\begin{align*} P(E) = & \frac{1}{N} \\ = & \frac{1}{6} \\ = & \frac{1}{6} \end{align*}\]
Por essa razão sabe-se, a priori a probabilidade de ocorrência de qualquer evento ao se realizar esse tipo de experimento aleatório uma única vez.
4.2.4.2 Conceito frequentista ou a posteriori
Todavia, se realizarmos o experimento aleatório anterior apenas algumas, tal regularidade poderá não ser comprovada: as frequências observadas (as quantidades obtidas para cada um dos valores numéricos das faces) apresentarão uma grande irregularidade diferindo das frequência teóricas definidas.
Observa-se que os resultados das frequências observadas irá se estabilizar, aproximando-se das frequências teóricas, à medida que se repete esse experimento um número suficientemente grande de vezes.
A definição frequencial (a posteriori):
1- refere-se à probabilidade empírica observada a posteriori; 2- tem por objetivo estabelecer um modelo adequado à interpretação de alguns tipos de experimentos aleatórios; e, 3- é a base para se formular um modelo teórico de distribuição de probabilidades como os que serão abordados mais adiante.
Ao se repetir o experimento aleatório um grande número de vezes ( \(n\) tendendo a infinitas vezes), a quantidade de vezes que um determinado resultado foi verificado dividida por o número de repetições realizadas (\(n\)) irá se aproximar de sua proporção teórica. É o que se denomina como regularidade estatística dos resultados por essa propriedade não mais se necessita que os eventos sejam equiprováveis.
Formalmente conhecida como Lei Fraca dos Grandes Números (um dos pilares da teoria da probabilidade, foi formalizada pelo matemático suíço Jakob Bernoulli em 1713) e estabelece uma convergência para a probabilidade: à medida que o número de ensaios independentes de um experimento aleatório aumenta, a frequência relativa dos sucessos observados tende a se aproximar da probabilidade teórica
\[ P\left(E\right)=\underset{n\to \infty }{lim}{\frac{F(E)}{n}} \]
onde:
- \(P(E)\) é a probabilidade de ocorrência do evento \(E\);
- \(F(E)\) é a frequência observada do evento \(E\) (o número de vezes que ele ocorre em n repetições); e,
- \(n\) é o número de repetições do experimento.
Jakob Bernoulli in 1713
4.2.4.2.1 Simulações
As simulações desempenham um papel fundamental no entendimento prático dos conceitos probabilísticos, permitindo a reprodução de experimentos aleatórios em larga escala.
Por meio de simulações, podemos verificar empiricamente a convergência das frequências observadas para as frequências teóricas discutidas nos conceitos anteriores.
Elas fornecem uma ferramenta poderosa para ilustrar a regularidade estatística dos resultados, especialmente em situações em que realizar o experimento real seria impraticável ou custoso.
Ao simular o lançamento de um dado, por exemplo, é possível observar como a frequência relativa de qualquer face começa a se aproximar da probabilidade teórica (\(P(\cdot)=\frac{1}{6}\)) à medida que aumentamos o número de repetições.
# Função para lançar o dado n vezes e calcular a frequência de uma face específica
lancar_dado <- function(n, face_escolhida) {
# Definindo as faces do dado
faces <- 1:6
# Realizando n lançamentos
lancamentos <- sample(faces, n, replace = TRUE)
# Calculando a frequência observada da face escolhida
frequencia <- sum(lancamentos == face_escolhida) / n * 100
# Exibindo a frequência em percentual
cat("A frequência observada da face", face_escolhida, "foi de", frequencia, "%\n")
}## A frequência observada da face 3 foi de 20 %## A frequência observada da face 3 foi de 16.44 %
Ao simular o lançamento de um dado, por exemplo, é possível observar como as frequências relativas de todas as faces começam a se aproximar das probabilidades teóricas (\(P(1)=P(2)=P(3)=P(4)=P(5)=P(6)=\frac{1}{6}\)) à medida que aumentamos o número de repetições.
library(ggplot2)
lanca_dado <- function(numero_de_lancamentos) {
# Gere os lançamentos do dado
lancamentos <- sample(1:6, numero_de_lancamentos, replace = TRUE)
# Crie um data frame com os resultados
dados <- data.frame(Face = lancamentos)
# Contagem das ocorrências de cada face
contagem <- table(dados$Face)
# Crie um gráfico de barras com o número de lançamentos no título
grafico <- ggplot(data = data.frame(Face = names(contagem), Contagem = as.numeric(contagem)),
aes(x = Face, y = Contagem)) +
geom_bar(stat = "identity") +
labs(x = "Face do Dado", y = "Contagem") +
ggtitle(paste("Lançamento de um Dado por:", numero_de_lancamentos, "vezes")) +
theme_minimal()
# Exiba o gráfico
print(grafico)
}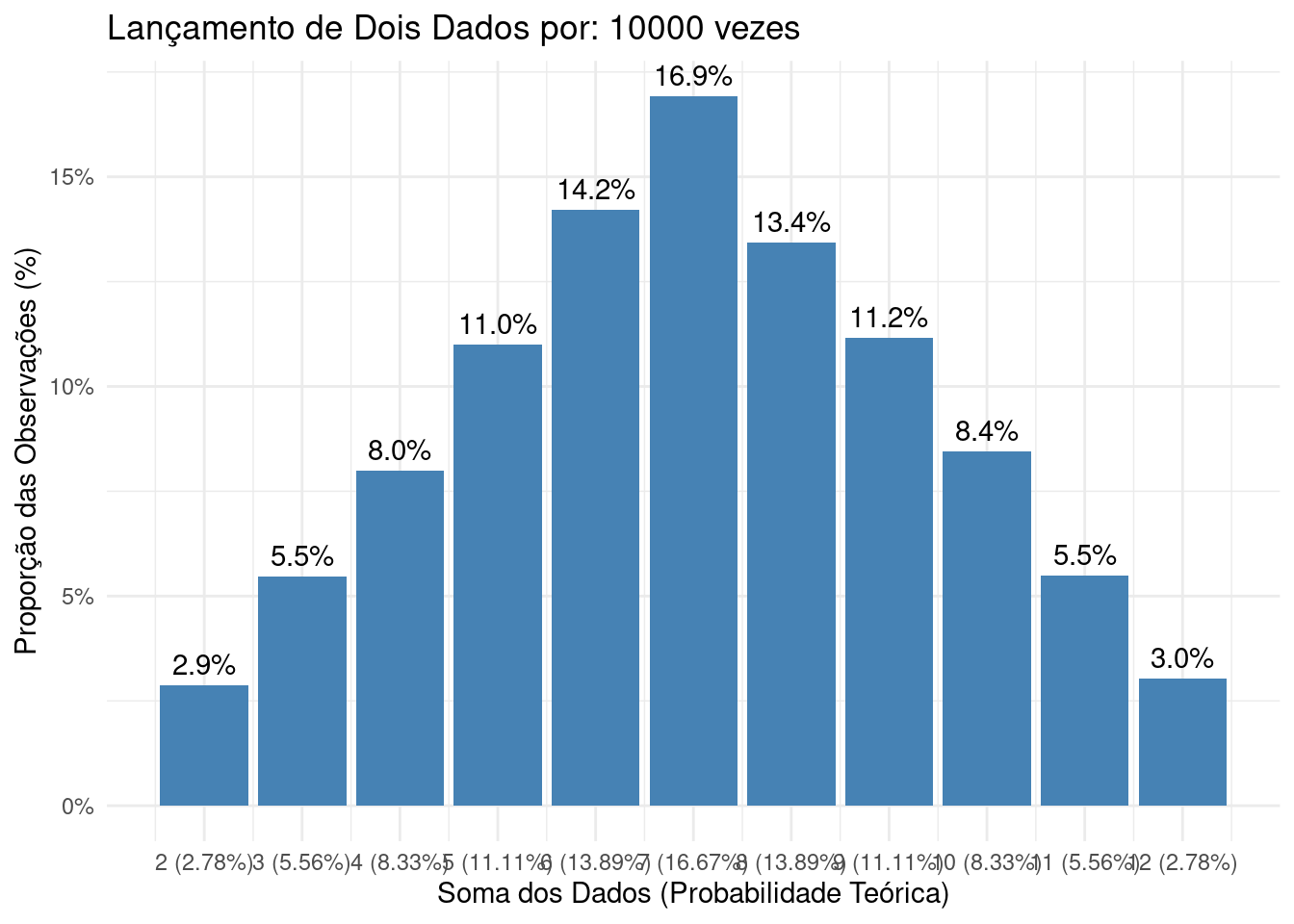
Figure 4.9: Histograma das frequências observadas em 10 lançamentos de um dado justo, evidenciando a variabilidade significativa nas frequências relativas, mesmo que todos os resultados sejam igualmente prováveis.
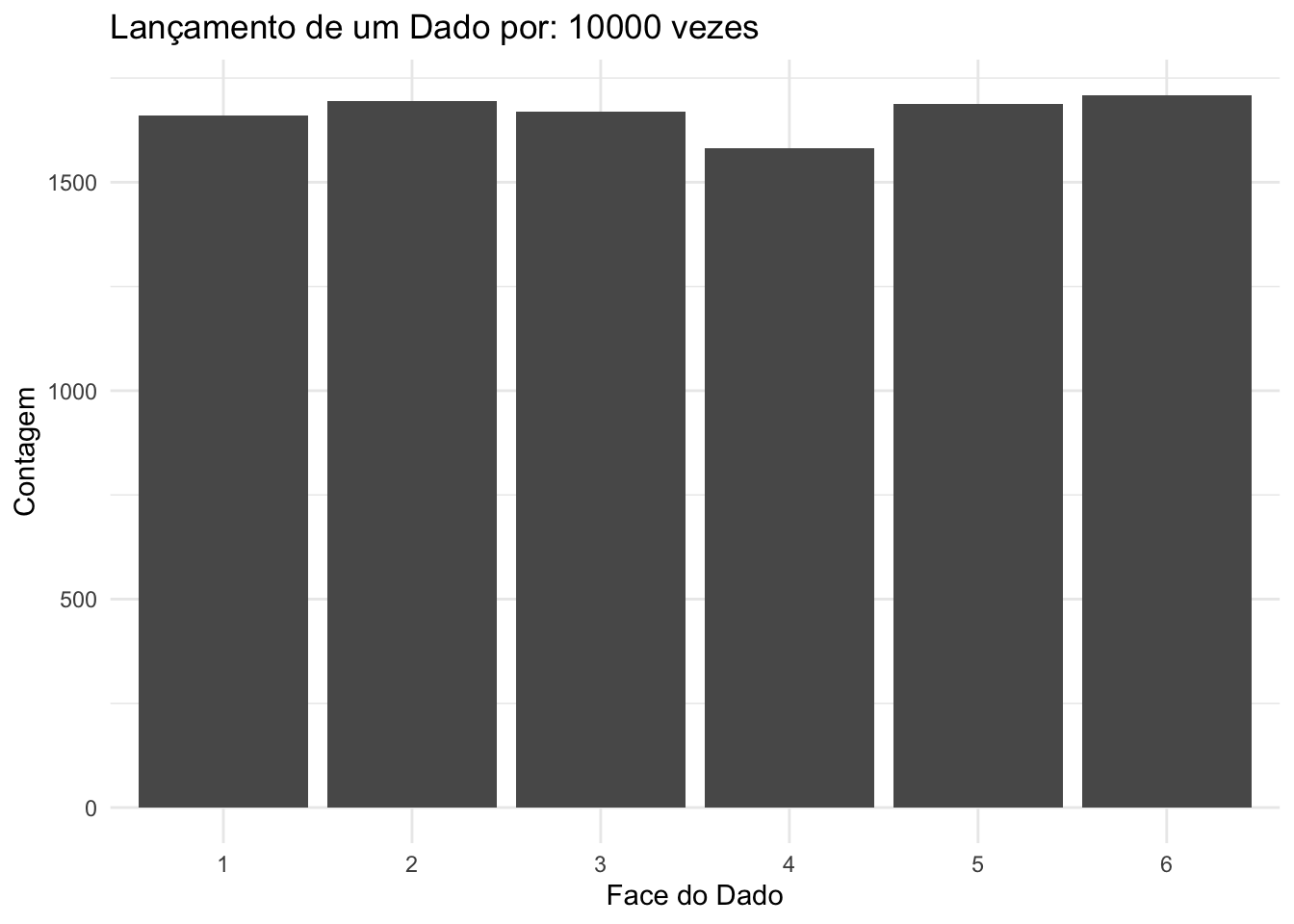
Figure 4.10: Histograma das frequências observadas em 10.000 lançamentos de um dado justo, ilustrando a convergência assintótica das frequências relativas de cada resultado para sua probabilidade teórica, considerando que todos os resultados são igualmente prováveis.
Ao simular o lançamento de dois dados, por exemplo, é possível observar como as frequências relativas de todas as possíveis somas das faces começam a se aproximar das probabilidades teóricas:
\[ P(2) = P(12) = \frac{1}{36}, \\ P(3) = P(11) = \frac{2}{36}, \\ P(4) = P(10) = \frac{3}{36}, \\ P(5) = P(9) = \frac{4}{36}, \\ P(6) = P(8) = \frac{5}{36}, \\ P(7) = \frac{6}{36} \]
à medida que aumentamos o número de repetições.
library(ggplot2)
lanca_dois_dados <- function(numero_de_lancamentos) {
# Gere os lançamentos dos dois dados
dado1 <- sample(1:6, numero_de_lancamentos, replace = TRUE)
dado2 <- sample(1:6, numero_de_lancamentos, replace = TRUE)
# Calcule a soma dos dois dados
somas <- dado1 + dado2
# Crie um data frame com os resultados
dados <- data.frame(Soma = somas)
# Contagem das ocorrências de cada soma
contagem <- table(dados$Soma)
# Crie um data frame com a proporção de cada soma
dados_grafico <- data.frame(
Soma = as.numeric(names(contagem)),
Contagem = as.numeric(contagem),
Proporcao = as.numeric(contagem) / numero_de_lancamentos
)
# Probabilidades teóricas de cada soma
prob_teoricas <- c(1/36, 2/36, 3/36, 4/36, 5/36, 6/36, 5/36, 4/36, 3/36, 2/36, 1/36)
somas_teoricas <- 2:12
prob_teoricas_formatadas <- paste0("(", round(prob_teoricas * 100, 2), "%)")
# Adicione as probabilidades teóricas ao eixo x como rótulos
labels_eixo_x <- paste(somas_teoricas, prob_teoricas_formatadas)
# Crie o gráfico de barras com as frequências observadas e as probabilidades teóricas no eixo x
grafico_somas <- ggplot(data = dados_grafico, aes(x = Soma, y = Proporcao)) +
geom_bar(stat = "identity", fill = "steelblue") +
geom_text(aes(label = scales::percent(Proporcao, accuracy = 0.1)), vjust = -0.5) + # Exibe as proporções acima das barras
scale_x_continuous(breaks = somas_teoricas, labels = labels_eixo_x) + # Define os rótulos com soma e probabilidade
scale_y_continuous(labels = scales::percent) + # Formata o eixo y como porcentagem
labs(x = "Soma dos Dados (Probabilidade Teórica)", y = "Proporção das Observações (%)") +
ggtitle(paste("Lançamento de Dois Dados por:", numero_de_lancamentos, "vezes")) +
theme_minimal()
# Exiba o gráfico
print(grafico_somas)
}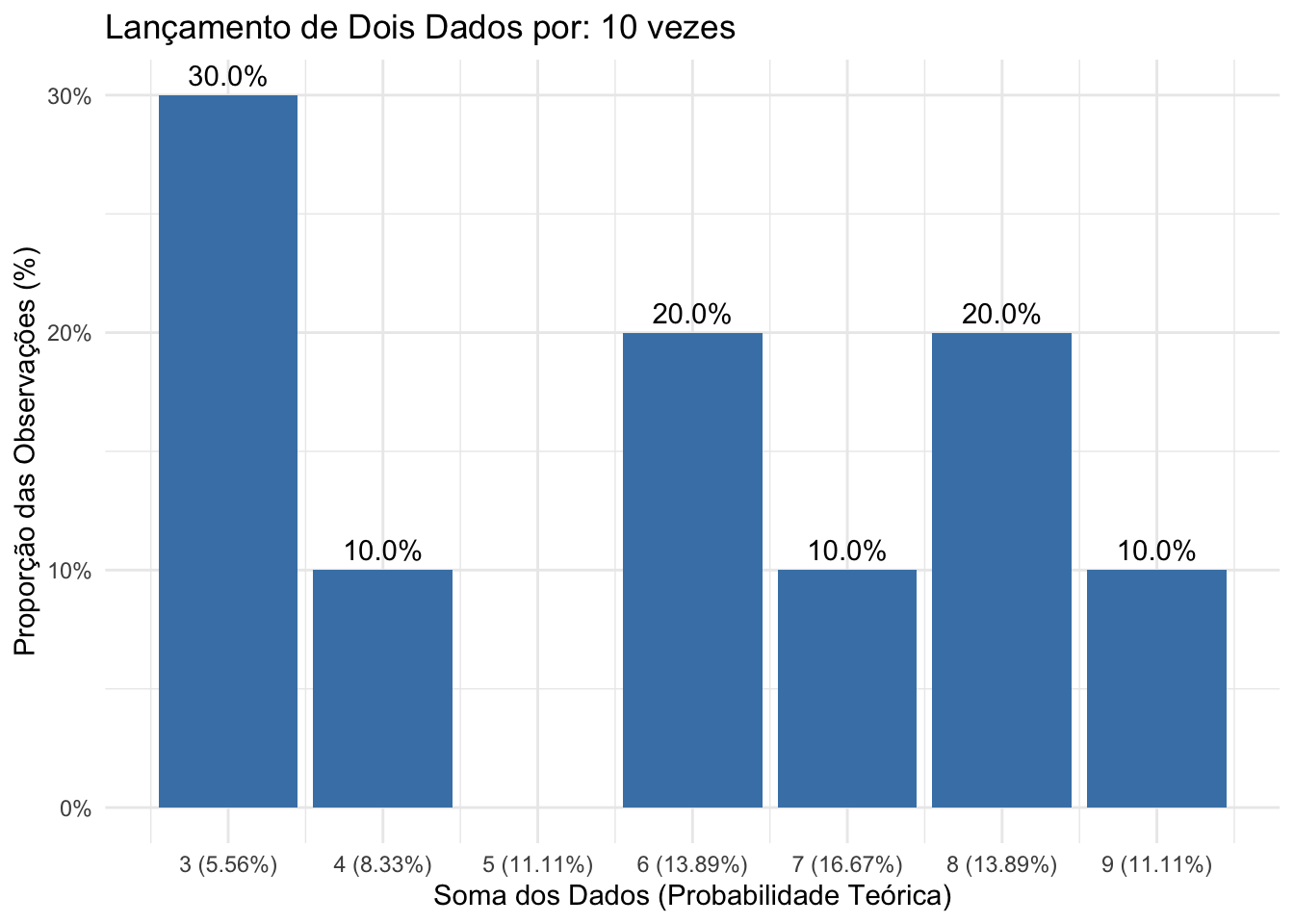
Figure 4.11: Histograma das frequências observadas em 10 lançamentos de dois dados justos, evidenciando a diferença significativa das frequências relativas observadas em relação às probabilidades teóricas de cada resultado possível.
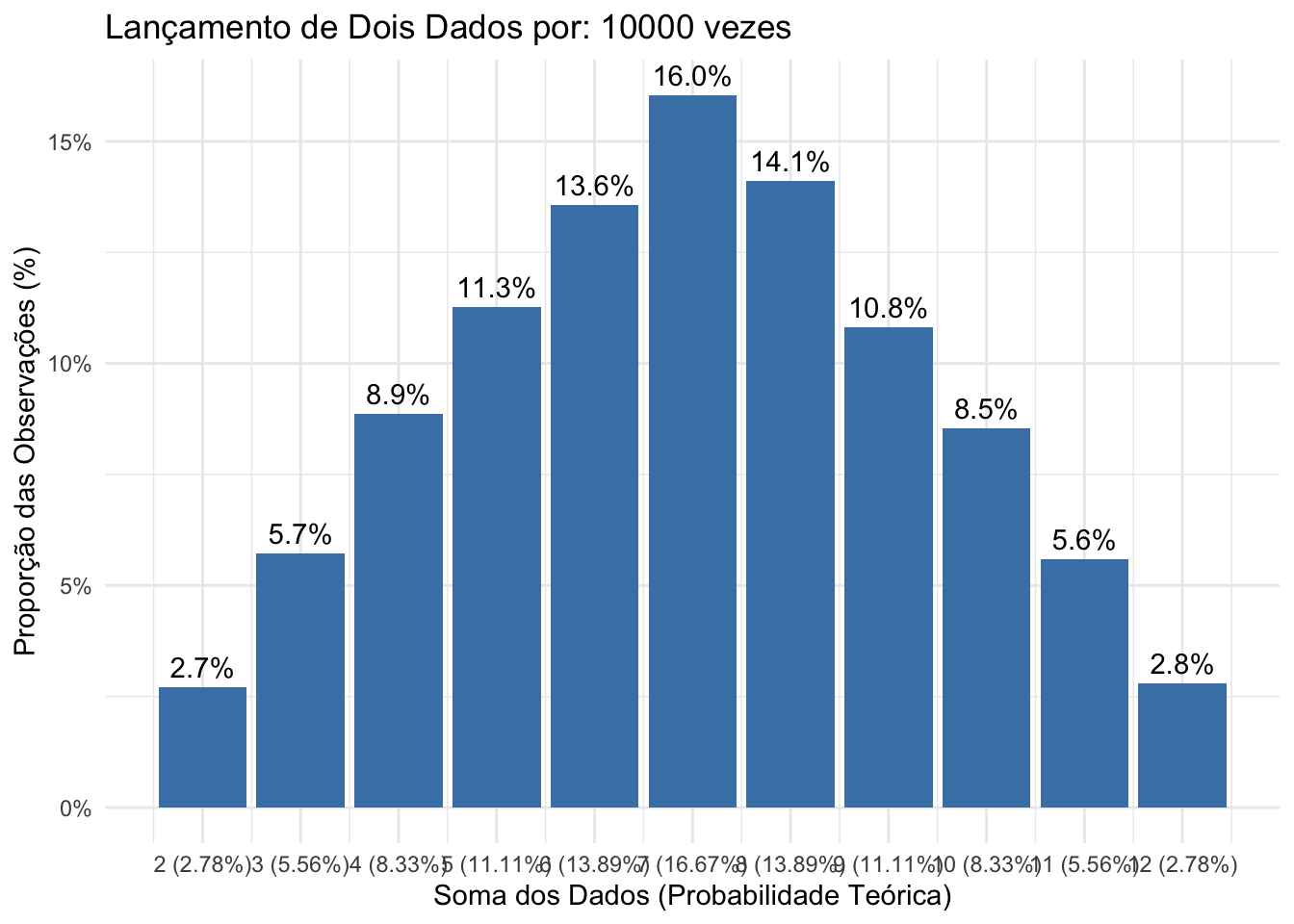
Figure 4.12: Histograma das frequências observadas em 10.000 lançamentos de dois dados justos ilustrando a convergência assintótica das frequências relativas observadas para as probabilidades teóricas de cada resultado possível.
4.2.4.3 Conceito axiomático
Esta abordagem é baseada em um conjunto de axiomas matemáticos que definem as propriedades básicas de probabilidades. A probabilidade é definida como uma função de conjuntos que atribui a cada conjunto de eventos um número entre 0 e 1, satisfazendo os axiomas matemáticos de probabilidade. Essa abordagem permite que as probabilidades sejam definidas formalmente e usadas para cálculos matemáticos.
Um axioma é uma premissa considerada necessariamente evidente e verdadeira, fundamento de uma demonstração, porém ela mesma indemonstrável, originada, segundo a tradição racionalista, de princípios inatos da consciência ou, segundo os empiristas, de generalizações da observação empírica.
Admita \(P\) uma função que opera sobre o espaço \(\Omega\); isto é, uma função que associa uma quantidade \(P(\Omega)\) a cada elemento \(\omega\) \(\in\) \(\Omega\).
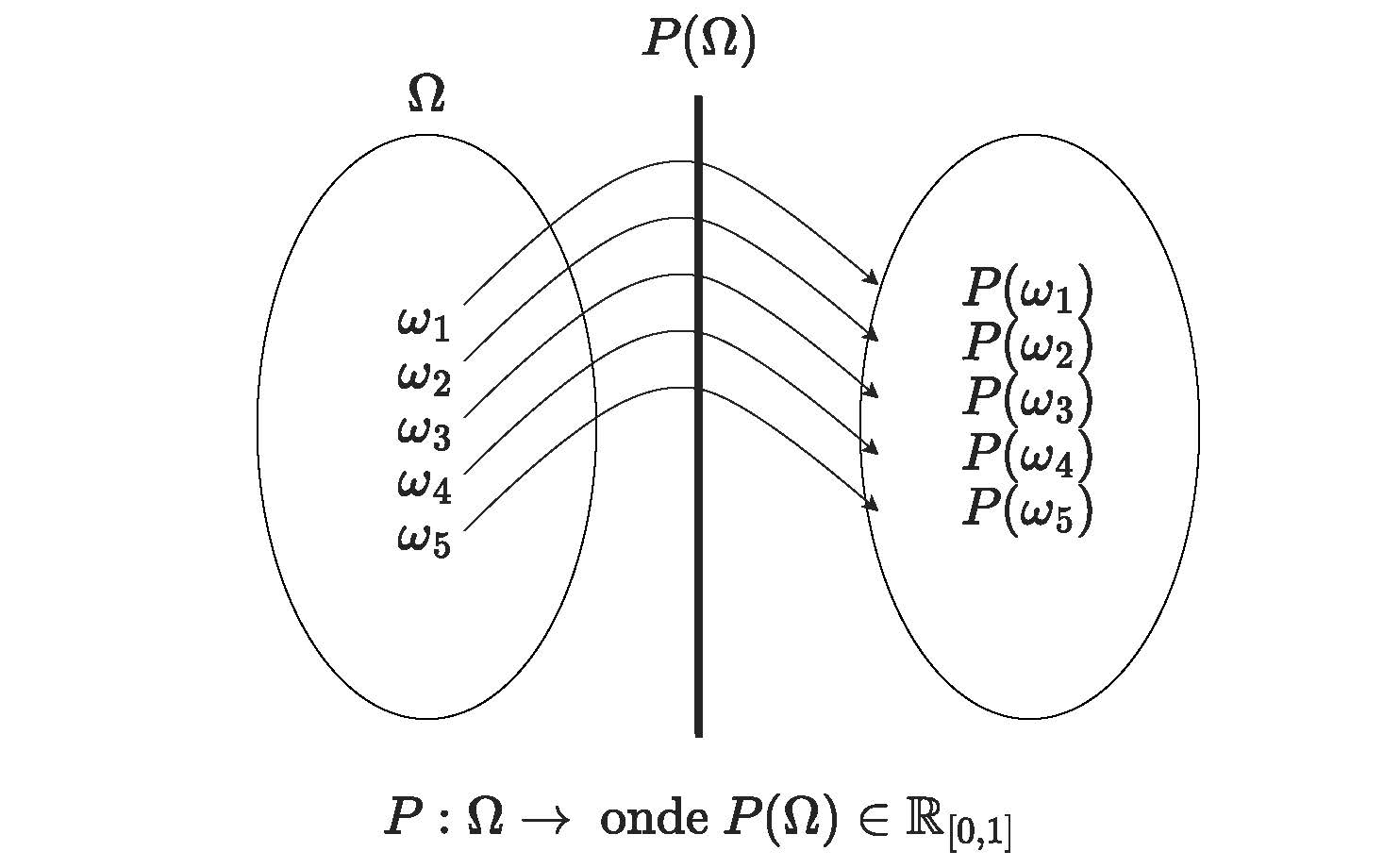
Figure 4.13: Representação gráfica da função \(P(\Omega)\)
Essa função \(P\) será uma função de probabilidade se, e somente se, satisfizer a três axiomas (postulados: conceitos iniciais necessários à construção ou aceitação de uma teoria) estabelecidos por Andrey Kolmogorov (1933).

Figure 4.14: Andrey Nikolaevich Kolmogorov (1903-1987)
Kolmogoroff afirmou que uma Teoria das probabilidades poderia ser desenvolvida a partir de axiomas, da mesma forma que a geometria e a álgebra, e a considerou como caso especial da Teoria da medida e integração desenvolvida por Lebesgue, Borel e Fréchet. Ele estabeleceu como postulados as propriedades comuns das noções de probabilidade clássica e frequentista que, desta forma, viraram casos particulares da definição axiomática.
4.2.4.3.1 Postulado do intervalo
A probabilidade de qualquer \(E\) é um número real entre 0 e 1 (pode-se entender isso como uma convenção, onde então se estabelece a medida da probabilidade é um número positivo e que qualquer evento pode ter probabilidade de, no máximo, 1). Esse postulado está plenamente de acordo com a interpretação frequentista de probabilidade.
\[ P(E) \ge 0 \text{ (não negatividade e,)}\\ \text{mais especificamente, }\\ 0 \hspace{0.5cm} \le P(E) \hspace{0.5cm} \le 1 \]
4.2.4.3.2 Postulado da certeza (normalização)
O segundo postulado refere-se à probabilidade do evento certo ser igua a 1. No que diz respeito à interpretação frequentista, uma probabilidade de 1 implica que o evento em questão ocorrerá 100% do tempo ou, em outras palavras, que é certo que ele ocorra (como, p. exemplo, um experimento aleatório de se lançar dois dados e somar o valor de suas faces o evento certo poderia ser definido como observar uym valor menor que 13 ou maior que 2)
\[ P(\Omega) = 1 \]
4.2.4.3.3 Postulado da aditividade para eventos mutuamente exclusivos (aditividade)
\[ P\left(\bigcup _{n=1}^{\infty }{\omega}_{n}\right)=\sum _{n=1}^{\infty }P\left({\omega}_{n}\right) \]
para qualquer sequência de eventos mutuamente exclusivos \(\{\omega_{1}, \omega_{2}, \omega_{3}, ..., \omega_{n}, ...\}\) (isto é, tal que \(\omega_{i} \cap \omega_{j} \varnothing\) se \(i \neq j\))
Tomando o terceiro postulado no caso mais simples, isto é, para dois eventos mutuamente exclusivos \(\omega_{1}\) e \(\omega_{2}\), pode ser facilmente visto que é satisfeito pela interpretação frequentista.
Se um evento ocorrer, digamos, 28% das vezes, outro evento ocorrerá 39%, e os dois eventos não podem ocorrer ao mesmo tempo (ou seja, são mutuamente exclusivos), então um ou outro evento} ocorrerão em 28 + 39 = 67% das vezes. Assim, o terceiro postulado é satisfeito, e o mesmo tipo de argumento se aplica quando há mais de dois eventos mutuamente exclusivos.
Recapitulando
1- foi definido o conceito de experimento aleatório como sendo aquele cujos resultados não podem ser determinados com certeza antes de sua realização;
2- foi definido o conceito de espaço amostral de um experimento aleatório como sendo o conjunto de todos os possíveis resultados que ele pode apresentar;
3- foi definido que um evento de interesse é um subconjunto do espaço amostral no qual estamos particularmente interessados;
4- foi definida uma função que tem como domínio o espaço amostral e associa uma quantidade (entre 0 e 1) a cada elemento do espaço amostral; e, por fim,
5- estabelecemos que se essa função atende a três postulados então ela será uma medida da probabilidade de ocorrẽncia de cada evento do espaço amostral em questão.
Assim, quando uma função \(P\) associa uma quantidade \(P(\Omega)\) a um evento \(\omega\) e \(P(\Omega)\) atende aos três axiomas anteriormente estabelecidos, diz-se que que ela é a função de probabilidade de \(\Omega\).