7.12 Dimensionamento de amostras
7.12.1 Erros
Há de distinguir dois tipos de erros associados a levamentamentos amostrais:
- erros amostrais, as diferenças entre o resultado obtido em uma amostra específica (uma estatística) e seu verdadeiro valor na população (o parãmetro);
- erros não amostrais (experimentais), decorrentes de dados amostrais coletados incorretamente, inconsistentemente, fruto de erros nas transcrições, delineamentos fracamente estabelecidos (resultando em amostras tendenciosas), leituras instrumentais imprecisas (resultantes da perda da calibração dos instrumentos ou operação por técnicos com diferentes habilidades).
Os erros amostrais ocorrem porque as amostras são aleatórias: se de um grupo de 100 números extrairmos uma amostra aleatória de 10 deles a média amostral calculada teria um valor diferente a cada diferente amostra extraída (essa flutuação é assunto da teoria da distribuição das médias e proporções amostrais). Já os erros não amostrais devem ser minimizados ou melhor não existir.
A determinação do tamanho de uma amostra (\(n_{0}\)) é função do erro amostral tolerável e do nível de significância \(\alpha\) estabelecido a priori pelo pesquisador que se relaciona ao nível de confiança pretendido por \((1-\alpha)\).
Assim, se o nível de significância máximo admissível para o assunto pesquisado é \(\alpha=0,05\), o nível de confiança será \((1-\alpha)=0,95\) (uma vez que: \(\alpha + (1-\alpha)=1\)).
| Níveis de confiança (1 − α): | 0,80 | 0,90 | 0,95 | 0,99 | 0,999 |
| Níveis de significância α: | 0,20 | 0,10 | 0,05 | 0,01 | 0,001 |
| zc | 1,28 | 1,64 | 1,96 | 2,57 | 3,29 |
Todavia, como mais adiante se verá, há situações nas quais o valor crítico referente ao nível de confiança estabelecido e que será empregado no dimensionamento da amostra será obtido de uma outra distribuição (t de Student).
7.12.2 Determinação do tamanho de uma amostra para estimação da média populacional
Determinação do tamanho \(n_{0}\) de uma amostra para estimação da média considerando-se uma população infinita (\(N \ge 20.n_{0}\)) e seguindo uma distribuição Normal:
\[ n_{0} = \frac{z_{c}^2 \cdot \sigma^2}{\varepsilon^2} \]
em que:
- \(n_{0}\): é o tamanho amostral;
- \(z_{c}\): valor crítico tabelado da distribuição Normal usado para o nível de significância desejado (por exemplo, para \(\alpha\)=5%, \(z_{c}=1,96\));
- \(\sigma\) desvio padrão populacional obtido em estudos prévios; e,
- \(\varepsilon\): é o erro amostral, a máxima diferença entre \(\mu\) e \(\stackrel{-}{x}\) que se espera observar sob um nível de confiança de (\(1-\alpha\)) .
Exemplo: Qual o tamanho de amostra necessária para se estimar o peso médio de cervos em uma dada população sob estudo, admitida infinita. Sabe-se de estudos anteriores que o desvio padrão \(\sigma\) do peso para animais dessa idade é de 30 kg. Utilize um erro \(\varepsilon\) de 10 kg na estimação e um nível confiança \((1-\alpha)\) de 95%.
\[\begin{align*} n_{0} & = \frac{Z^{2} \cdot \sigma^{2}}{\varepsilon^{2}} \\ n_{0} & = \frac{1,96^{2} \cdot 30^{2}}{10^{2}} \\ n_{0} & \sim 35 \end{align*}\]
Se a população não pode ser considerada infinita, ou seja, se \(N < 20.n_{0}\), então aplica-se uma correção sobre o valor inicialmente calculado para a (\(n_{0}\)) obtendo-se um novo tamanho (\(n\)):
\[ n=\frac{N \cdot n_{0}}{N + n_{0}} \]
No exemplo anterior, caso a população sob estudo fosse composta por apenas 200 animais (\(N < 20.n_{0}\)) o tamanho da amostra seria:
\[\begin{align*} n & = \frac{N \cdot n_{0}}{N + n_{0}} \\ n & = \frac{200 \cdot 35}{200 + 35 } \\ n & \sim 30 \end{align*}\]
O conhecimento prévio do desvio padrão populacional (\(\sigma\)) para utilizar as expressões acima é quase que uma exceção. Na maioria dos estudos ele é desconhecido e a única informação disponível acerca da variabilidade é o desvio padrão amostral \(S\).
Nesse cenário, a variável Norma padronizada \(Z\) é substituída por uma outra, que segue a distribuição “t” de Student e, para se obter seu valor crítico \(t_{c}\) para um determinado nível de confiança desejado necessitamos ter uma informação adicional: os graus de liberdade (gl ou df), que são iguais ao tamanho da amostra menos 1 (\(gl=n_{0}-1\)). Observa-se que para \(n \to \infty\), os valores críticos de \(z_{c}=t_{c}\) para um mesmo nível de significância.
Ocorre porém que, não tendo ainda sido retirada a amostra, não dispomos do valor de \(s\). Se não conhecemos nem ao menos um limite superior para \(\sigma\), a única solução será colher uma amostra piloto de \(n_0\) elementos para, com base nela obtermos uma estimativa de \(s\) e estimarmos o tamanho amostral pela expressão:
\[
n = \frac{t_{c}^2 \cdot s^2}{\varepsilon^2}
\]
com \(s\) calculado sobre a amostra piloto de \(n_{0}\) elementos e com \(t_{c}\) obtido em uma tabela de valores da distribuição ``t’’.
Essas tabelas de valores consideram nas suas colunas variados níveis de sginificância \(\alpha\) e, nas suas linhas uma informação chamada de graus de liberdade (gl)
Graus de liberdade não mais são, no contexto estudado, que o tamanho da amostra piloto \(n_{0}\) menos 1 (\(gl=n_{0}-1\). Assim, se a amostra piloto for de 5 elementos, gl=4 e será nessa linha, junto à coluna do nível de significância desejado, que o valor “t” será encontrado.
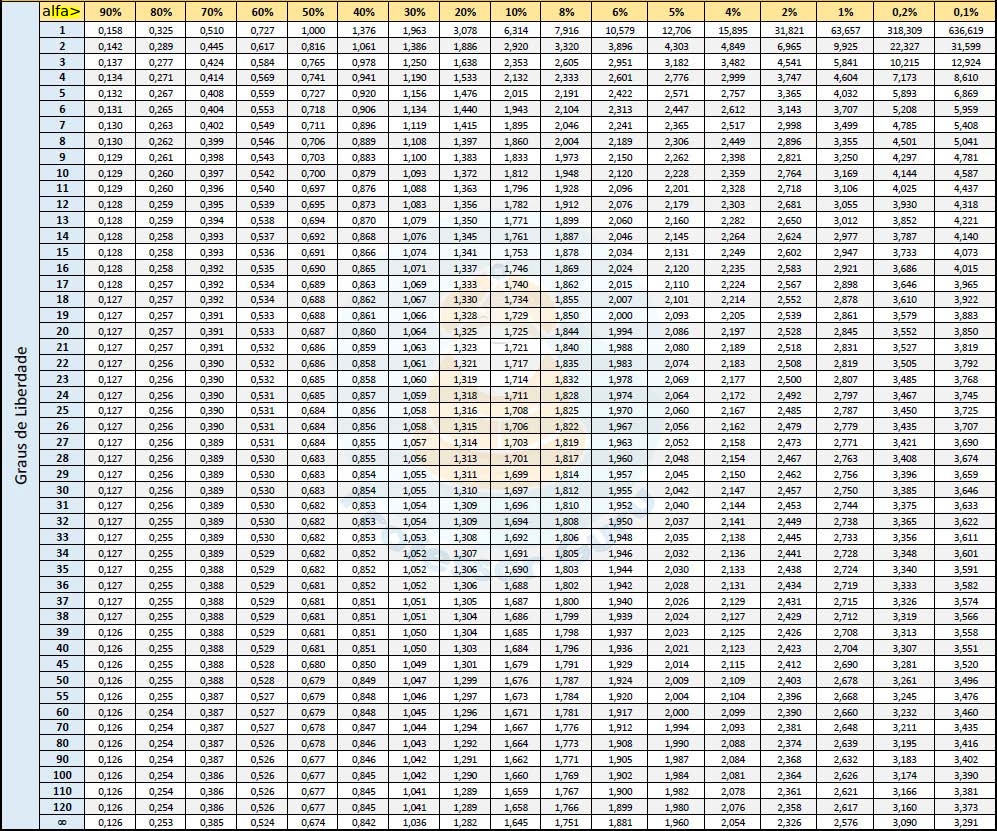
Figure 7.10: Tabela t de Stdent: cada linha refere-se a um gl e cada coluna a um nível de significância (no cruzamento tem-se o valor crítico de t sob essas condições)
Observe que à medida que o tamanho da amostra cresce, o valor crítico \(t_{c}\) se aproxima do valor crítico \(_{c}\) para um mesmo nível de significância. Por exemplo, para um \(\alpha=5\%\) uma amostra de 121 (df=121-1=120) elementos possui um valor crítico \(t_{c}=1,96\) (na distribuição de Student) e um valor crítico \(z_{c}=1,96\) (distribuição Normal padrão).
Se \(n \le n_{0}\), a amostra piloto já terá sido suficiente para ser usada na análise. Caso contrário, deve-se retirar mais elementos da população, recalcular o tamanho da amostra \(n\) até se observe essa desigualdade.
7.12.2.1 Margem de erro em uma estimativa amostral da média
Reescrevendo-se a expressão para a determinação do tamanho amostral podemos exprimir o erro \(\varepsilon\) associado à estimativa obtida de uma amostra de tamanho \(n\): \(\hat{p}\) da média populacional
\[ \varepsilon = z_{c}\cdot \sqrt{\frac{\sigma^{2}}{n}} \]
em que \(\varepsilon\) é uma quantidade para mais e para menos da estimativa obtida de uma amostra de tamanho \(n\) em relação a \(\mu\) sob o nível de confiança \(1-\alpha\) que determina \(z_{c}\).
A expressão anterior considera que a variâcia popuacional \(\sigma^{2}\) é conhecida. Caso não se tenha informação alguma sobre seu valor, seguem-se as mesmas considerações relacionadas ao tamanho \(n\) da amostra:
- se \(n \ge 30\), adotar a variância amostral \(S^{2}\) como aproximação de \(\sigma^{2}\);
- se \(n < 30\), adotar a variância amostral \(S^{2}\) como aproximação de \(\sigma^{2}\) usando-se o valor crítico \(t_{c}\) da distribuição de Student (com gl/df iguais ao tamanho da amostra menos 1)
7.12.3 Determinação do tamanho de uma amostra para estimação da proporção populacional
A determinação do tamanho de uma amostra para estimação da proporção populacional considerando-se uma população infinita (\(N \ge 20. n_{0}\)):
\[ n_{0} = \frac{z_{c}^{2} \cdot \pi \cdot (1- \pi) }{\epsilon^{2}} \]
em que:
- \(n_{0}\) é o tamanho da amostra;
- \(z_{c}\) é valor crítico tabelado da distribuição Normal para o nível de significância desejado (por exemplo, para \(\alpha\)=5%, \(z_{c}\)=1,96);
- \(\pi\) é a proporção populacional;
- \(\varepsilon\): é o erro amostral, a máxima diferença entre \(\pi\) e \(p\) que se espera observar sob um nível de confiança de (\(1-\alpha\)) .
Quando não se dispõe de nenhuma informação a priori sobre a proporção populacional (\(\pi\)) a adoção do máximo valor possível ao produto: \(\pi . (1- \pi )=\frac{1}{4}\) assegura que o o tamanho de amostra obtido será suficiente para a estimação qualquer que seja a proporção populacional \(\pi\).
Isso equivale a considerar:
\[ n_{0} = \frac{z_{c}^{2}}{\epsilon^{2}} \cdot \frac{1}{4} \]
De modo análogo, se a população não pode ser considerada infinita (\(N < 20n_{0}\)) aplica-se uma correção sobre o valor calculado do tamanho da amostra (\(n_{0}\)) chegando-se a um novo tamanho (\(n\)):
\[ n=\frac{N \cdot n_{0}}{N + n_{0}} \]
Exemplo:Qual o tamanho de amostra (\(n_{0}\)) suficiente para estimarmos a proporção da área com solo contaminado que necessita de certo tratamento de descontaminação, com precisão (\(\varepsilon\)) de 0,02 e um nível de confiança (\(1-\alpha\)) de 95%, sabendo que essa proporção seguramente não é superior a 0,2?
\[\begin{align*} n_{0} & = \frac{z_{c}^{2} \cdot \pi \cdot (1-\pi) }{\varepsilon^{2}} \\ n_{0} & = \frac{1,96^{2} \cdot 0,20 \cdot 0,80 }{0,02^{2}}\\ n_{0} & \sim 1.537 \end{align*}\]
Considerando-se uma estimativa conservadora para \(\pi.(1-\pi)\) pelo máximo valor possível desse produto (\(\frac{1}{4}\)) teremos:
\[\begin{align*} n_{0} & = \frac{z_{c}^{2}}{\varepsilon^{2}} \cdot \frac{1}{4} \\ n_{0} & = \frac{1,96^{2}}{0,02^{2}} \cdot \frac{1}{4} \\ n_{0} & = 2.401 \end{align*}\]
7.12.3.1 Margem de erro em uma estimativa amostral da proporção
Reescrevendo-se a expressão para a determinação do tamanho amostral para a situação na qual não temos nenhuma informação sobre a proporção populacional (\(\pi\)), podemos exprimir o erro \(\varepsilon\) associado à estimativa da proporção (\(p\)) obtida de uma amostra de tamanho \(n\) da proporção populacional (\(\pi\)) sob o nível de confiança (\(1-\alpha\)) pelo critério mais conservador (\(\pi.(1-\pi)=\frac{1}{4}\))
\[\begin{align*} \varepsilon & = z_{c}\cdot \sqrt{\frac{\pi\cdot \left(1-\pi\right)}{n}} \\ \varepsilon & = z_{c}\cdot \sqrt{\frac{\frac{1}{4}}{n}} \end{align*}\]
em que \(\varepsilon\) é uma quantidade para mais e para menos da estimativa \(p\) obtida de uma amostra de tamanho \(n\) em relação a \(\pi\) sob o nível de confiança \(1-\alpha\) que determina \(z_{c}\).
Exemplo: Uma pesquisa recente mostra o apoio dos eleitores a uma posição de liberação das restrições sobre a pesquisa de células estaminais embrionárias e permitir o uso médico do princípio ativo da . A pesquisa realizada para o descobriram que 50% dos prováveis eleitores de Michigan apoiam a proposta de células-tronco, 32% são contra e 18% indecisos. A pesquisa telefônica ouviu 602 prováveis eleitores de Michigan. Qual a margem de erro a um nível de significância de 95% para os eleitores a favor da liberação das pesquisas? (link: Elgin C. College)
\[\begin{align*} \varepsilon & = {z}_{(\frac{\alpha }{2})}\cdot \sqrt{\frac{\hat{p}\cdot \left(1-\hat{p}\right)}{n}}\\ & = 1,96 \cdot \sqrt{\frac{0,50 \cdot \left(1- 0,50 \right)}{602}}\\ & = 0,04 \end{align*}\]
A margem de erro é de 4 pontos percentuais para cima ou para baixo (46%; 54%) na proporção de eleitores em relação à proporção populacional \(\pi\) a favor da liberação das pesquisas, sob um um nível de confiança de 95%
| 95% CI for Cohen | ||||||
| cline6-7 | t | df | p | Cohen | Lower | Upper |
| 1-7 engagement | 2.365 | 38 | 0.023 | 0.748 | 0.101 | 1.385 |