3.4 Medidas de forma (assimetria & curtose)

Quando analisamos o histograma (a representação gráfica da distribuição das frequências dos valores agrupados em classes) de uma determinada variável, não é muito comum que ele se mostre simétrico tal como seria se os dados fossem distribuídos de modo exatamente Normal.

Ao observarmos que a cauda se mostra mais alongada para a direita (indicativo da existência de uma quantidade maior de dados com grandes valores, arrastando a média para a direita: moda \(<\) mediana \(<\) média) diz-se que a distribuição é assimétrica à direita. Na situação oposta (moda \(>\) mediana \(>\) média) diz-se que ela é assimétrica à esquerda.

a=rbeta(10000,5,2)
c=rbeta(10000,5,5)
b=rbeta(10000,2,5)

par(mfrow=c(1,3))
hist(a, 
     xlab="Valores",col = 'lightblue',
     ylab="Frequência",
     main="Assimetria à esq.")
hist(c, 
     xlab="Valores",col = 'lightblue',
     ylab="Frequência",
     main="Relativa simetria")
hist(b, 
     xlab="Valores",col = 'lightblue',
     ylab="Frequência",
     main="Assimetria à dir.")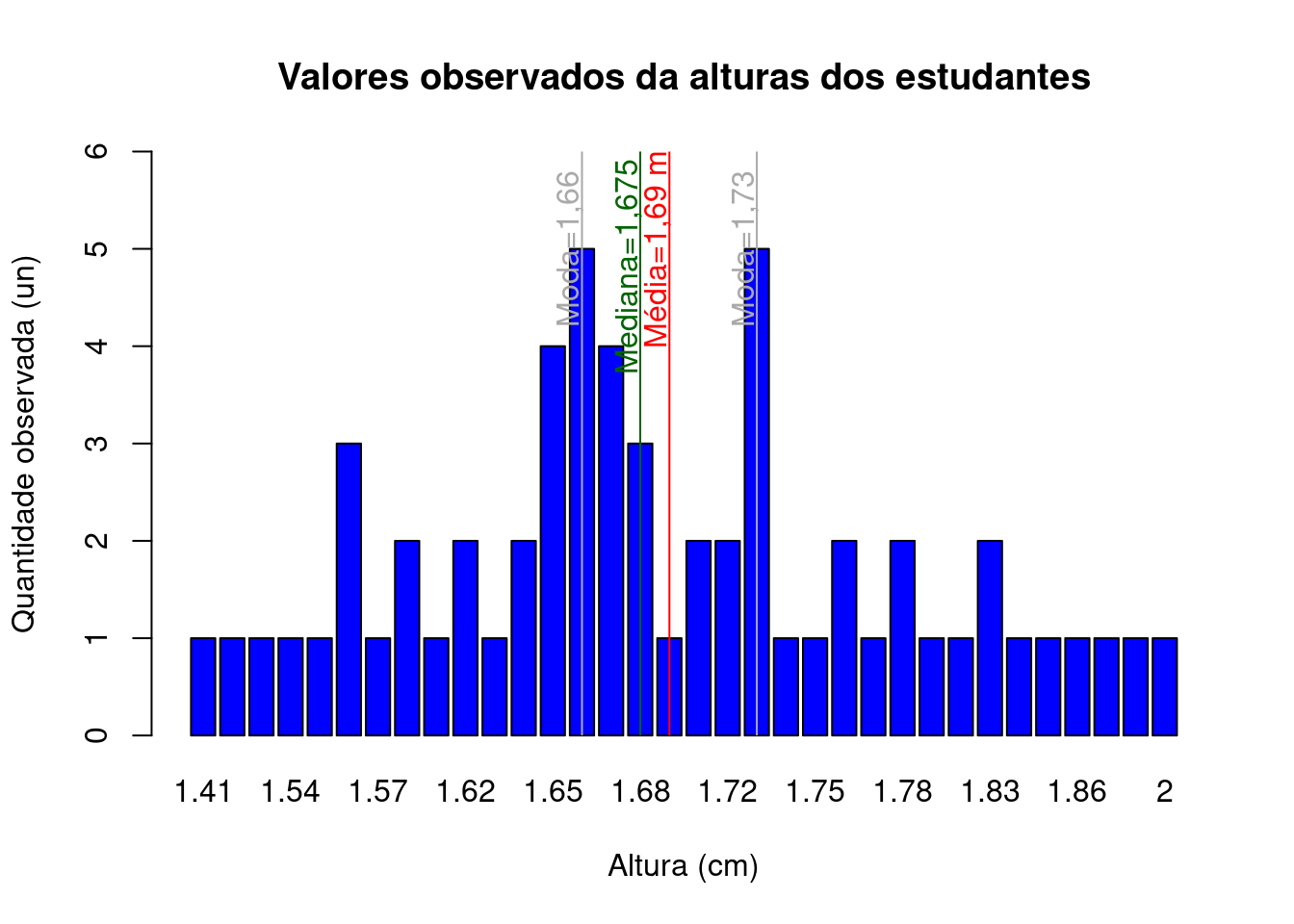

Figure 3.12: Diferentes formas na distribuição dos dados

De modo assemelhado, o histograma pode denotar uma forma mais plana ou menos aguda, onde um cume mostra-se mais destacado.

Nesse aspecto da forma, uma variável com distribuição Gaussiana apresentaria uma curva a que denominamos mesocúrtica. Distribuições com um aspecto mais plano são denominadas de platicúrticas e as com um cume agudo são denominadas leptocúrticas.

A curtose é uma medida da agudeza da distribuição dos dados em relação à distribuição Gaussiana.

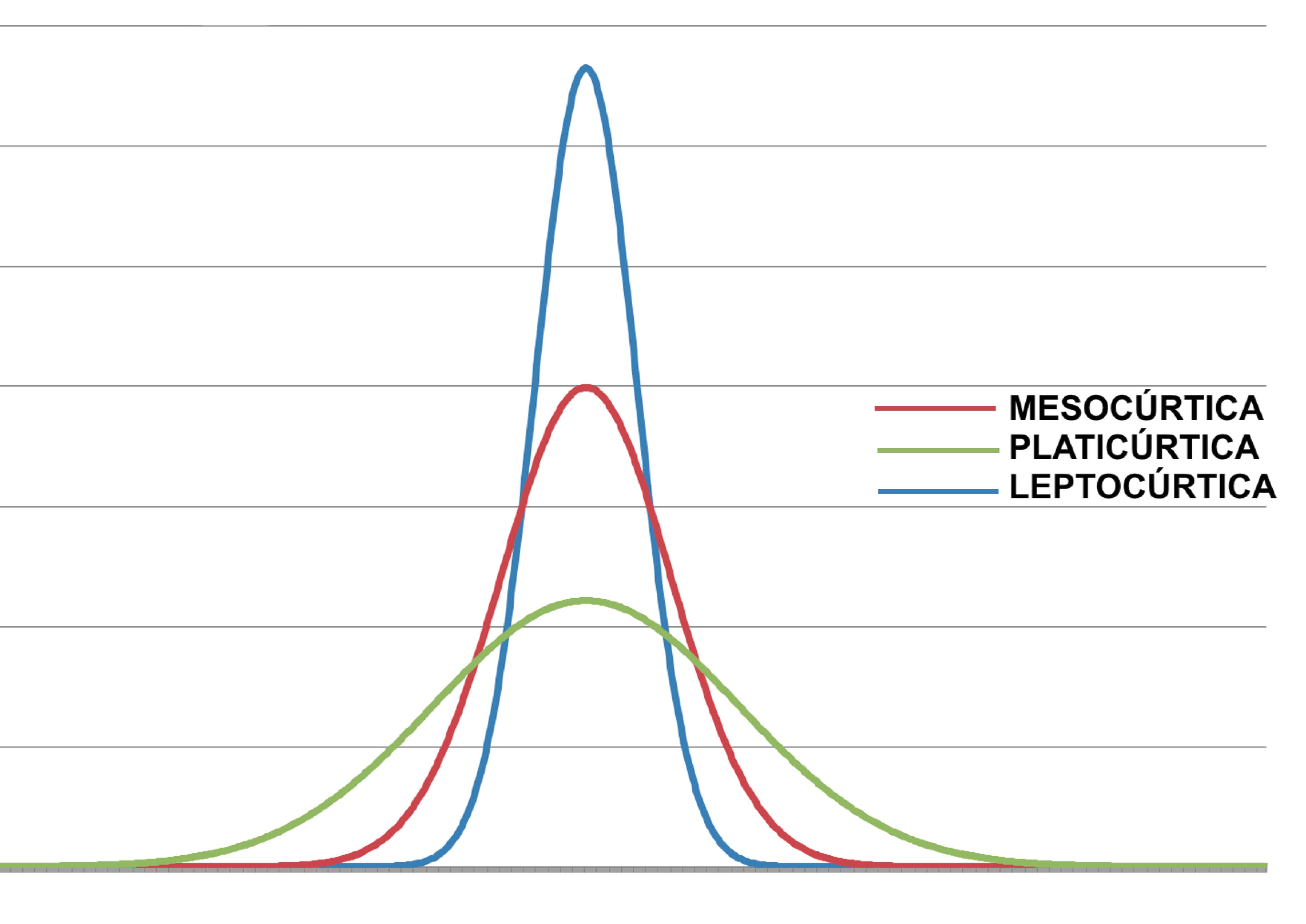
Figure 3.13: Diferentes aspectos de uma distribuição quanto à sua inclinação

Essas possíveis variações na forma de uma distribuição podem ser numericamente quantificadas através dos coeficientes de assimetria e curtose.

Uma das medidas do coeficiente de assimetria é através do primeiro ou segundo coeficientes de Pearson, dados pelas seguintes relações:

Primeiro coeficiente de assimetria de Pearson: \(AS= \frac{ \stackrel{-}{x} - M_{o} }{ s }\)
Segundo coeficiente de assimetria de Pearson: \(AS = \frac{ 3 ( \stackrel{-}{x} - M_{d}) } { s }\)

Onde:

\(\stackrel{-}{x}\) é a média;
\(M_{o}\) é a moda;
\(S\) é o desvio padrão; e,
\(M_{d}\) é a mediana.

A assimetria é classificada do modo seguinte:

\(-1 \leq AS \leq 1%=\) : distribuição simétrica;
\(AS<-1\): distribuição com assimetria negativa; e,
\(AS>1\): distribuição com assimetria positiva.

Uma das medidas do coeficiente de curtose é através da seguinte relação entre quartis e percentis:

\[ K = \frac{Q_{3} - Q_{1}} {2 \times(P_{90} - P_{10})} \]

Onde:

\(Q_{3}\) = \(3^{o}\) quartil;
\(Q_{1}\) = \(1^{o}\) quartil;
\(P_{90}\) = \(90^{o}\) percentil; e,
\(P_{10}\) = \(10^{o}\) percentil.

O coeficiente de curtose é classificado do modo seguinte:

k = 0,263: distribuição mesocúrtica;
k < 0,263: distribuição leptocúrtica; e,
k > 0,263: distribuição platicúrtica.