9.1 Distribuições amostrais

Parâmetro é toda medida numérica descritiva de uma população. Quando essas medidas são calculadas sobre amostras extraídas de uma população passam a ser denominadas como estatísticas da população de origem. A média, a mediana, a variância, a proporção amostrais, assim como outras estatísticas amostrais, são exemplos de variáveis aleatórias (v.a.) uma vez que seus valores sofrem variação a cada amostra extraída.

Considere uma população com \(N\) elementos da qual se deseja extrair todas as possíveis amostras de tamanho \(n\). Para cada amostra extraída pode-se calcular uma mesma medida descritiva como, por exemplo, a média ( ou a variância, proporção ). O conjunto dos valores resultantes nos permite analisar como as estimativas amostrais se distribuem em comparação ao parâmetro que estão a estimar.

Essas distribuições são denominadas distribuições amostrais. O estudo das distribuições amostrais é um elemento fundamental na inferência estatística posto possibilitar o estabelecimento de intervalos de confiança relacionados ao valor de um parâmetro que se deseja inferir, a partir de uma estatística proveniente de uma única amostra.

O processo de extração de amostras pode ser com ou sem reposição. A extração com reposição assegura a independência entre os eventos e, eventos independentes são mais facilmente analisados.

O quantidade possível de amostras de tamanho \(n\) extraídas de uma população de tamanho \(N\) é dado por :

• com reposição: \(N^{n}\); e,
• sem reposição: \(C_{(N.n)}\)

Mais adiante veremos que processos de extração de amostras de tamanho \(n\), sem reposição de populações finitas com parâmetros \(\mu\) (média) e \(\sigma^{2}\) (variância) a esperança da v.a. de sua média amostral ainda é dada por:

\[ E(\stackrel{-}{X})=\mu \]

mas sua variância deve ser corrigida de:

\[ Var(\stackrel{-}{X}) =\frac{\sigma^{2}}{n} \]

para:

\[ Var(\stackrel{-}{X}) =\frac{\sigma^{2}}{n} \cdot (\frac{N-n}{N-1}) \]

em que \((\frac{N-n}{N-1})\) é denominado como fator de correção para populações finitas.

Para ilustrar o conceito de distribuição das médias amostrais considere uma situação onde uma empresa produz lâmpadas e a vida útil média, em horas, dessas lâmpadas segue uma distribuição Normal tal que \(VU \sim N (1600, 120)\).

Usando conceitos já explicados em uma unidade anterior podemos determinar o tamanho amostral em função de:

• um erro máximo: \(\varepsilon\)=20 horas;
• um nível de significância estabelecido: \(\alpha\)=0,05; e,
• e alguma informação sobre a medida da variabilidade da variável em estudo: \(\sigma\)=120 horas (no caso, o desvio padrão populacional).

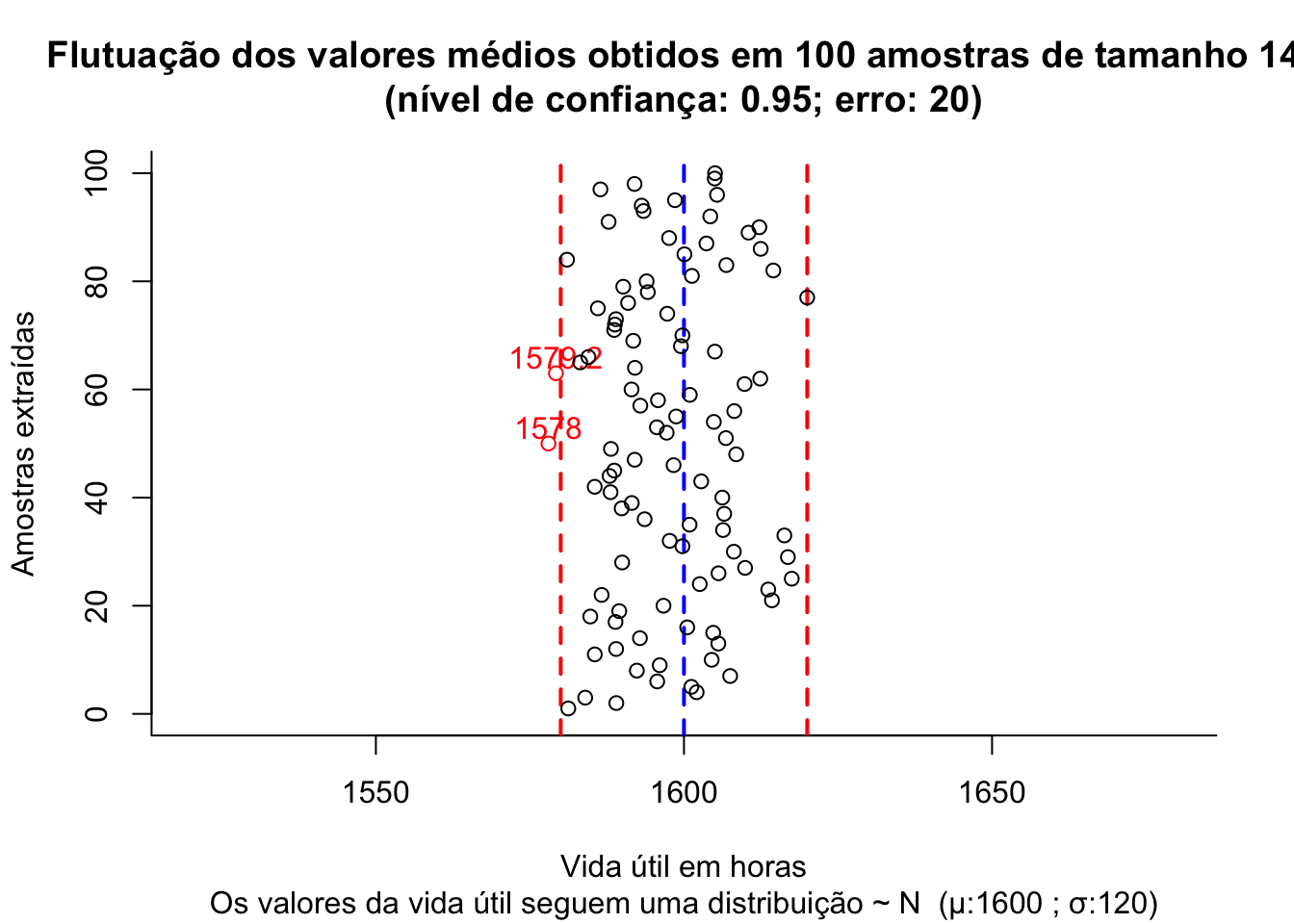
Figure 9.1: Flutuação dos valores médios para diversas amostras extraídas de uma mesma população distribuição \(\sim N (\mu; \sigma)\)

##       mu media      erro   li   ls
## 1   1600  1581 -18.77472 1563 1600
## 2   1600  1589 -10.97742 1570 1608
## 3   1600  1584 -16.02810 1565 1603
## 4   1600  1602   2.05613 1582 1622
## 5   1600  1601   1.20191 1579 1623
## 6   1600  1596  -4.34379 1576 1615
## 7   1600  1607   7.49691 1588 1627
## 8   1600  1592  -7.64965 1574 1611
## 9   1600  1596  -3.93694 1576 1616
## 10  1600  1605   4.50021 1587 1622
## 11  1600  1586 -14.47447 1566 1605
## 12  1600  1589 -11.01366 1568 1610
## 13  1600  1606   5.57670 1586 1626
## 14  1600  1593  -7.14743 1573 1613
## 15  1600  1605   4.74872 1587 1623
## 16  1600  1601   0.53062 1580 1621
## 17  1600  1589 -11.11033 1570 1608
## 18  1600  1585 -15.20467 1564 1605
## 19  1600  1589 -10.50270 1571 1608
## 20  1600  1597  -3.32321 1576 1617
## 21  1600  1614  14.27793 1593 1636
## 22  1600  1587 -13.36661 1568 1605
## 23  1600  1614  13.67541 1594 1633
## 24  1600  1603   2.56419 1581 1624
## 25  1600  1617  17.49048 1597 1638
## 26  1600  1606   5.60686 1587 1624
## 27  1600  1610   9.92061 1592 1627
## 28  1600  1590 -10.03119 1569 1611
## 29  1600  1617  16.86217 1596 1638
## 30  1600  1608   8.09218 1588 1628
## 31  1600  1600  -0.24914 1581 1618
## 32  1600  1598  -2.32077 1579 1616
## 33  1600  1616  16.29513 1596 1637
## 34  1600  1606   6.33935 1586 1627
## 35  1600  1601   0.90618 1581 1620
## 36  1600  1594  -6.38629 1576 1611
## 37  1600  1607   6.52489 1587 1626
## 38  1600  1590 -10.11281 1570 1609
## 39  1600  1592  -8.47433 1573 1611
## 40  1600  1606   6.21919 1587 1626
## 41  1600  1588 -11.91608 1567 1609
## 42  1600  1586 -14.48404 1563 1608
## 43  1600  1603   2.79523 1585 1620
## 44  1600  1588 -12.07283 1568 1608
## 45  1600  1589 -11.31198 1567 1610
## 46  1600  1598  -1.68381 1579 1618
## 47  1600  1592  -7.99769 1571 1613
## 48  1600  1608   8.47350 1587 1630
## 49  1600  1588 -11.85023 1569 1607
## 50  1600  1578 -21.99265 1559 1597
## 51  1600  1607   6.80242 1588 1626
## 52  1600  1597  -2.80714 1579 1616
## 53  1600  1596  -4.40016 1575 1616
## 54  1600  1605   4.84530 1587 1623
## 55  1600  1599  -1.26801 1578 1620
## 56  1600  1608   8.16282 1588 1628
## 57  1600  1593  -7.08606 1572 1613
## 58  1600  1596  -4.21721 1575 1616
## 59  1600  1601   0.94888 1580 1622
## 60  1600  1591  -8.51121 1572 1611
## 61  1600  1610   9.84053 1590 1630
## 62  1600  1612  12.38096 1594 1631
## 63  1600  1579 -20.78719 1560 1599
## 64  1600  1592  -7.95328 1572 1612
## 65  1600  1583 -16.83196 1560 1606
## 66  1600  1584 -15.50517 1567 1602
## 67  1600  1605   5.01468 1587 1623
## 68  1600  1600  -0.49478 1579 1620
## 69  1600  1592  -8.23153 1573 1611
## 70  1600  1600  -0.25127 1583 1617
## 71  1600  1589 -11.31822 1569 1608
## 72  1600  1589 -11.20824 1569 1608
## 73  1600  1589 -11.03623 1568 1609
## 74  1600  1597  -2.71225 1577 1618
## 75  1600  1586 -13.97640 1569 1603
## 76  1600  1591  -9.06837 1571 1611
## 77  1600  1620  19.99916 1598 1642
## 78  1600  1594  -5.86872 1576 1612
## 79  1600  1590  -9.85716 1573 1608
## 80  1600  1594  -6.06212 1576 1611
## 81  1600  1601   1.28512 1583 1620
## 82  1600  1615  14.50179 1595 1634
## 83  1600  1607   6.87777 1588 1626
## 84  1600  1581 -18.97906 1564 1598
## 85  1600  1600   0.07629 1580 1620
## 86  1600  1612  12.44912 1590 1635
## 87  1600  1604   3.64708 1584 1623
## 88  1600  1598  -2.41768 1576 1619
## 89  1600  1610  10.48064 1591 1630
## 90  1600  1612  12.23519 1592 1632
## 91  1600  1588 -12.22954 1566 1609
## 92  1600  1604   4.27313 1583 1625
## 93  1600  1593  -6.55424 1573 1614
## 94  1600  1593  -6.86181 1573 1614
## 95  1600  1599  -1.45929 1579 1618
## 96  1600  1605   5.36790 1586 1625
## 97  1600  1586 -13.55530 1565 1608
## 98  1600  1592  -8.02092 1572 1612
## 99  1600  1605   4.99009 1585 1625
## 100 1600  1605   5.03932 1585 1625

Observa-se no gráfico acima que algumas das amostras (em vermelho), numa proporção igual ao nível de significância estabelecido quando do dimensionamento (5%), geram médias (amostrais) se afastam do valor médio na população mais que o erro estabelecido (20 h).