4.8 Teoremas da Teoria das probabilidades

4.8.1 Teorema 01

Se $E$ é um evento num espaço discreto $\Omega$, então $P(E)$ é igual à soma das probabilidades de ocorrência de todos os elementos do espaço amostral que satisfazem ao evento de interesse $E$ .

Sejam $E_{1},E_{2},E_{3},\dots$ a sequência finita ou infinita de eventos que satisfazem ao evento de interesse $E$. Assim, $E = E_{1} \cup E_{2} \cup E_{3}...$. Como $E_{1},E_{2},E_{3},\dots$ são eventos mutuamente exclusivos, pelo terceiro postulado das probabilidades teremos:

\[ P(E) = P(E_{1}) + P(E_{2}) + P(E_{3}) + ... \]

Exemplo: Lançamento de uma moeda duas vezes

Espaço amostral dos possíveis eventos (resultados): $\Omega = \{(cara, cara), (cara, coroa), (coroa, cara), (coroa, coroa)\}$

Evento de interesse $E$: obter ao menos uma cara
Eventos que satisfazem: $E_{1} =\{(cara, cara)\}$; $E_{2} =\{(cara, coroa)\}$; $E_{3} =\{(coroa, cara)\}$

A probabilidade de $E$ ($P(E)$)será a soma das probabilidades dos eventos que o satisfazem:

\[ P(E) = P(E_{1}) + P(E_{2}) + P(E_{3}) = \frac{1}{4} + \frac{1}{4} + \frac{1}{4} = \frac{3}{4} \]

4.8.2 Teorema 02

Se um experimento aleatório pode ter $N$ resultados possíveis e equiprováveis e um evento $E$ pode ter $n$ resultados que o satisfazem, então $P(E) = \frac{n}{N}$.

Sejam $E_{1},E_{2},E_{3},\dots,E_{N}$ os resultados do espaço amostral $\Omega$, cada um deles equiprovável ($P(E_{i} =\frac{1}{N}$). Se $E$ é a união de $n$ desses eventos mutuamente exclusivos, pelo terceiro postulado das probabilidades teremos:

\[\begin{align*} P(E) & = P(E_{1}) + P(E_{2}) + P(E_{3}) + ... P(E_{n}) \\ P(E) & = \frac{1}{N} + \frac{1}{N} +\frac{1}{N} +...+\frac{1}{N} \\ P(E) & = \frac{n}{N} \end{align*}\]

4.8.3 Teorema 03

Se $E$ e $E^{c}$ são eventos complementares no espaço amostra $\Omega$ então $P(E^{c}) = 1 - P(E)$.

Sendo os eventos $E$ e $E^{c}$ mutuamente exclusivos e também sendo $E \cup E^{c} = \Omega$, considerando-se que $P(\Omega) = 1$, pelos segundo e terceiro postulados tem-se:

\[\begin{align*} P(\Omega) & = 1 \\ 1 & = P(E \cup E^{c}) \\ 1 & = P(E) + P(E^{c}) \end{align*}\]

4.8.4 Teorema 04

$P(\varnothing)=0$

Sendo $\Omega$ e $\varnothing$ são mutuamente exclusivos e, como de acordo com a definição de um espaço vazio $\Omega \cup \varnothing = \Omega$, pelo terceiro postulado tem-se:

\[\begin{align*} P(\Omega) & = P(\Omega \cup \varnothing)\\ P(\Omega) & = P(\Omega) + P(\varnothing)\\ P(\Omega) - P(\Omega) & = P(\varnothing)\\ P(\varnothing) & =0 \end{align*}\]

4.8.5 Teorema 05

Se $A$ e $B$ são eventos em um mesmo espaço amostral $\Omega$ e $A \subset B$ então $P(A) \le P(B)$.

Se $A \subset B$ então pode-se escrever: $B = A \cup (A^{c} \cap B)$ (verifica-se pelo correspondente diagrama de Venn).

Como $A$ e $A^{c}\cap B$ são mutuamente exclusivos, pelo terceiro postulado tem-se:

\[\begin{align*} P(B) & = P(A) + P(A^{c}\cap B) \\ P(A) & = P(B) - P(A^{c}\cap B) \end{align*}\]

4.8.6 Teorema 06

A probabilidade de qualquer evento $E$ em $\Omega$ está compreendida entre $0 \le P(E) \le 1$.

Estando $\varnothing \subset E \subset \Omega$ e considerando-se o Teorema 5 tem-se:

\[ P(\varnothing) \le P(E) \le P(\Omega) \\ 0 \le P(E) \le 1 \]

4.8.7 Teorema 07

Para dois eventos quaisquer em $\Omega$, $A$ e $B$ tem-se que: $P( A \cup B ) = P(A) + P(B) - P(A \cap B)$.

Sejam as seguintes probabilidades para esses eventos mutuamente exclusivos:

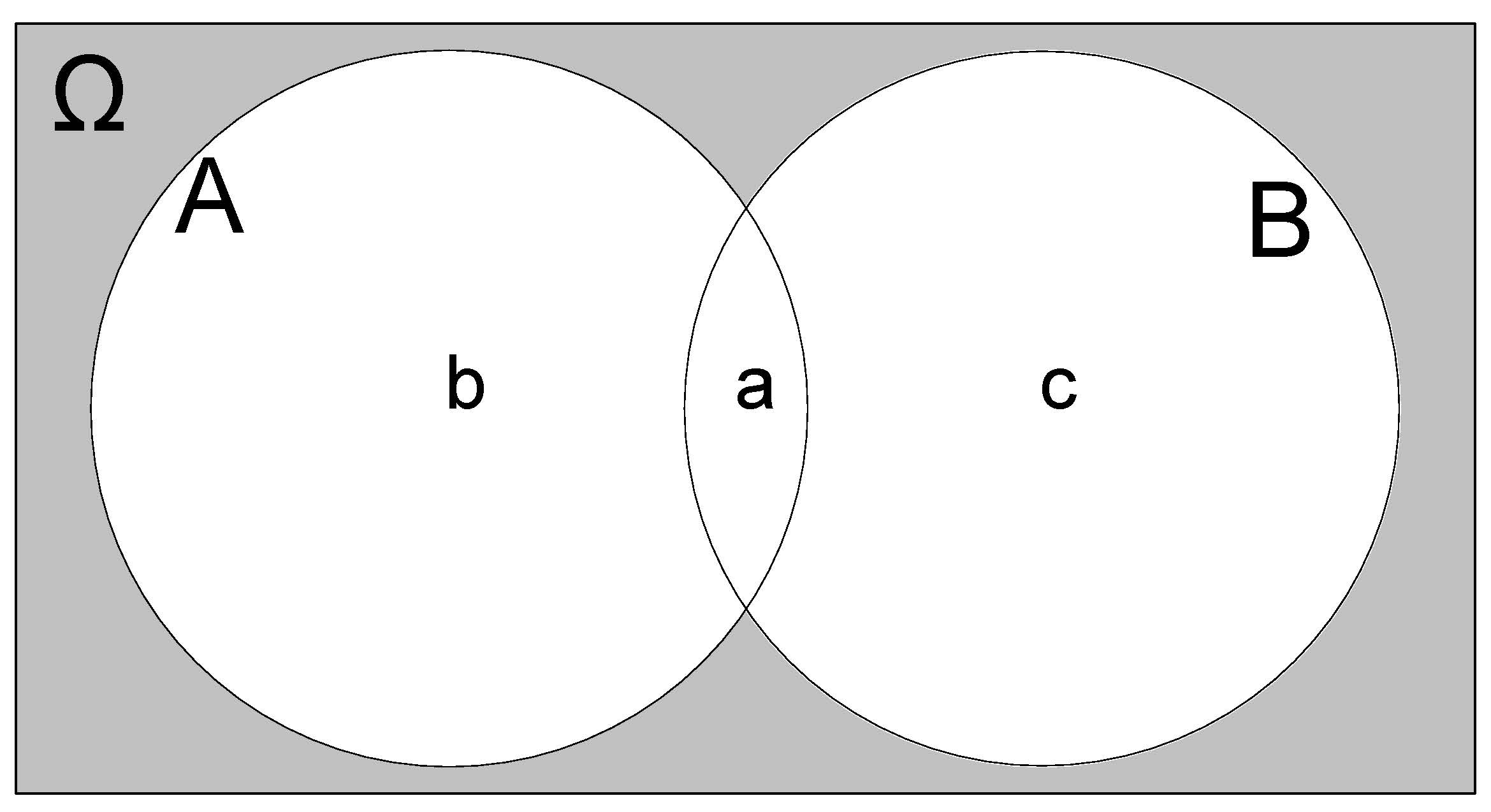
$P(A B) = a $;
$P(A \cap B^{c}) = b$; e,
$P(A^{c} \cap B) = c$.

\[\begin{align*} P ( A \cup B) & = a + b + c \\ P ( A \cup B) & = (a + b) + (c + d) - a \\ P ( A \cup B) & = P(A) + P(B) - P(A \cap B) \end{align*}\]

4.8.8 Teorema 08

Para três eventos quaisquer em $\Omega$, $A$, $B$ e $C$ tem-se que:

\[\begin{align*} P( A \cup B \cup C ) & = \\ & = P(A) + P(B) +P(C) - \\ & P(A \cap B) - P(A \cap C) - P(B \cap C) + \\ & P(A \cap B \cap C) \end{align*}\]

Escrevendo-se $A \cup B \cup C$ como $A \cup (B \cup C)$ e usando o Teorema 7 duas vezes (uma para $P[A \cup (B \cup C)]$ e a outra para $P( B \cup C)$ tem-se:

\[\begin{align*} P( A \cup B \cup C) & = P[ A \cup (B \cup C)] \\ P( A \cup B \cup C) & = P(A) + P( B \cup C) - P [A \cap (B \cup C)]\\ P( A \cup B \cup C) & = P(A) + P(B) + P(C) - P (B \cap C) - P [A \cap (B \cup C)] \end{align*}\]

Pela lei distributiva tem-se:

\[\begin{align*} P [A \cap (B \cup C)] & = P[ (A \cap B) \cup (A \cap C ) ]\\ P [A \cap (B \cup C)] & = P(A \cap B) + P(A \cap C) - P[ ( A \cap B) \cap (A \cap C)] \\ P [A \cap (B \cup C)] & = P(A \cap B) + P(A \cap C) - P( A \cap B \cap C) \end{align*}\]

Chega-se a :

\[\begin{align*} P( A \cup B \cup C ) & = \\ & P(A) + P(B) +P(C) - P(A \cap B) - P(A \cap C) - P(B \cap C) +\\ & P(A \cap B \cap C) \end{align*}\]