11.4 Natureza dos erros

Para introduzir os conceitos relacionados aos erros considere uma situação onde uma empresa produz lâmpadas e a vida útil média, em horas, dessas lâmpadas segue uma distribuição Normal tal que $VU \sim N (1600, 120)$.

Se não temos conhecimento algum sobre a real vida útil média dessas lâmpadas e alguém nos afirma que a vida útil é de 1.600 h, para confirmar ou não essa proposição (de um modo ``científico’’) devemos extrair uma amostra.

Usando conceitos já explicados em uma unidade anterior podemos determinar o tamanho amostral em função de:

um erro máximo tolerado: $\varepsilon$=20 horas;
um nível de significância estabelecido: $\alpha$=0,05; e,
e alguma informação sobre a medida da variabilidade da variável em estudo: $\sigma$=120 horas (no caso, o desvio padrão populacional).

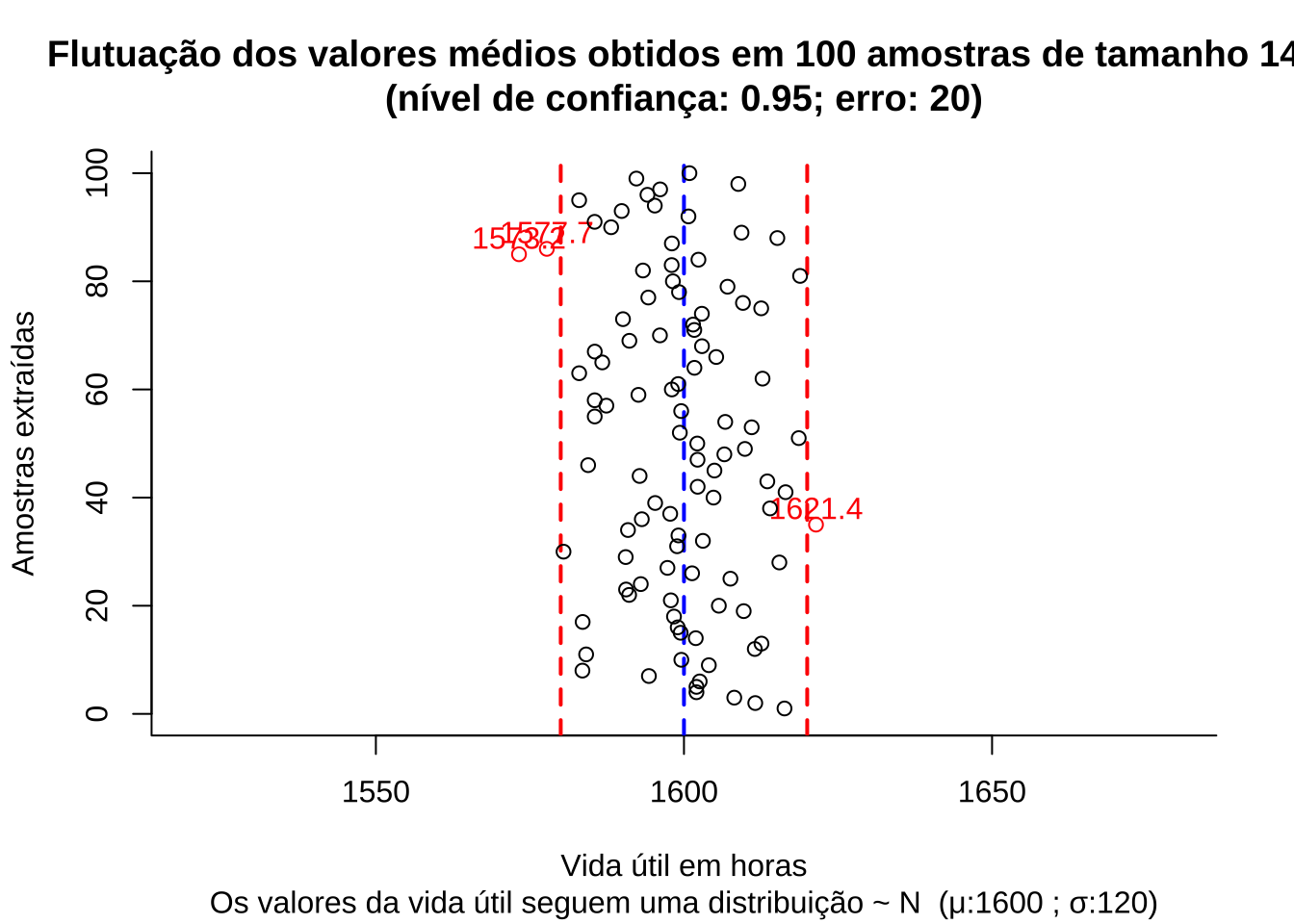
$Flutuação dos valores médios para diversas amostras extraídas de uma mesma população distribuição $\sim N (\mu; \sigma)$$

Figure 11.7: Flutuação dos valores médios para diversas amostras extraídas de uma mesma população distribuição $\sim N (\mu; \sigma)$

##       mu media     erro   li   ls
## 1   1600  1616  16.3151 1597 1636
## 2   1600  1612  11.5697 1593 1630
## 3   1600  1608   8.1650 1590 1627
## 4   1600  1602   2.0270 1583 1621
## 5   1600  1602   2.0289 1583 1621
## 6   1600  1603   2.5526 1582 1623
## 7   1600  1594  -5.6906 1576 1612
## 8   1600  1584 -16.4768 1564 1603
## 9   1600  1604   4.0345 1584 1624
## 10  1600  1600  -0.4252 1580 1619
## 11  1600  1584 -15.8765 1565 1603
## 12  1600  1611  11.4942 1592 1631
## 13  1600  1613  12.5781 1592 1633
## 14  1600  1602   1.9146 1581 1623
## 15  1600  1599  -0.5371 1580 1619
## 16  1600  1599  -1.0145 1580 1618
## 17  1600  1584 -16.4424 1562 1605
## 18  1600  1598  -1.6196 1577 1620
## 19  1600  1610   9.6945 1588 1631
## 20  1600  1606   5.6605 1586 1625
## 21  1600  1598  -2.1323 1579 1617
## 22  1600  1591  -8.9016 1573 1610
## 23  1600  1591  -9.3981 1569 1613
## 24  1600  1593  -7.0078 1573 1613
## 25  1600  1608   7.5389 1587 1628
## 26  1600  1601   1.3178 1580 1622
## 27  1600  1597  -2.6773 1579 1616
## 28  1600  1615  15.4813 1596 1635
## 29  1600  1591  -9.4544 1569 1612
## 30  1600  1580 -19.5474 1559 1602
## 31  1600  1599  -1.1140 1581 1617
## 32  1600  1603   3.0734 1584 1623
## 33  1600  1599  -0.8915 1581 1617
## 34  1600  1591  -9.0863 1570 1612
## 35  1600  1621  21.4264 1602 1641
## 36  1600  1593  -6.8440 1573 1613
## 37  1600  1598  -2.2345 1577 1618
## 38  1600  1614  13.9671 1596 1632
## 39  1600  1595  -4.6778 1576 1615
## 40  1600  1605   4.7965 1585 1625
## 41  1600  1616  16.4879 1598 1635
## 42  1600  1602   2.2212 1583 1621
## 43  1600  1614  13.5271 1593 1634
## 44  1600  1593  -7.1988 1574 1612
## 45  1600  1605   4.9445 1584 1626
## 46  1600  1584 -15.5532 1565 1604
## 47  1600  1602   2.2019 1582 1622
## 48  1600  1607   6.5546 1588 1625
## 49  1600  1610   9.8894 1590 1630
## 50  1600  1602   2.1602 1583 1621
## 51  1600  1619  18.6267 1599 1639
## 52  1600  1599  -0.6726 1578 1621
## 53  1600  1611  10.9881 1593 1629
## 54  1600  1607   6.6949 1588 1626
## 55  1600  1586 -14.4828 1566 1605
## 56  1600  1600  -0.4519 1580 1619
## 57  1600  1587 -12.5921 1566 1609
## 58  1600  1586 -14.4863 1565 1606
## 59  1600  1593  -7.3895 1572 1613
## 60  1600  1598  -1.9706 1579 1617
## 61  1600  1599  -0.9360 1581 1617
## 62  1600  1613  12.7514 1593 1633
## 63  1600  1583 -17.0069 1563 1603
## 64  1600  1602   1.6973 1580 1623
## 65  1600  1587 -13.2585 1567 1606
## 66  1600  1605   5.2341 1586 1624
## 67  1600  1586 -14.4755 1562 1609
## 68  1600  1603   2.9214 1583 1623
## 69  1600  1591  -8.8587 1571 1612
## 70  1600  1596  -3.9001 1575 1617
## 71  1600  1602   1.6750 1580 1623
## 72  1600  1601   1.4795 1584 1619
## 73  1600  1590  -9.8966 1569 1611
## 74  1600  1603   2.9040 1584 1622
## 75  1600  1613  12.5350 1592 1633
## 76  1600  1610   9.5725 1590 1630
## 77  1600  1594  -5.7881 1575 1614
## 78  1600  1599  -0.8031 1581 1618
## 79  1600  1607   7.0693 1587 1627
## 80  1600  1598  -1.7968 1579 1617
## 81  1600  1619  18.8460 1599 1639
## 82  1600  1593  -6.6569 1573 1613
## 83  1600  1598  -1.9942 1579 1617
## 84  1600  1602   2.3482 1582 1623
## 85  1600  1573 -26.7749 1551 1595
## 86  1600  1578 -22.2604 1560 1596
## 87  1600  1598  -1.9653 1578 1618
## 88  1600  1615  15.1544 1595 1635
## 89  1600  1609   9.3404 1591 1628
## 90  1600  1588 -11.8189 1569 1607
## 91  1600  1586 -14.4968 1564 1607
## 92  1600  1601   0.7246 1581 1620
## 93  1600  1590 -10.1073 1570 1610
## 94  1600  1595  -4.7349 1576 1615
## 95  1600  1583 -17.0122 1565 1601
## 96  1600  1594  -5.9265 1572 1616
## 97  1600  1596  -3.8663 1576 1616
## 98  1600  1609   8.8171 1590 1627
## 99  1600  1592  -7.7222 1574 1611
## 100 1600  1601   0.8865 1582 1620

Observa-se que algumas das amostras, numa proporção igual ao nível de significância estabelecido quando do dimensionamento (5%), apresentam médias com valores que se afastam do valor médio populacional mais que o erro estabelecido (20 h).

Como já informado anteriormente, um teste de hipóteses é um método quantitativo e não se baseia, sobremaneira, em impressões pessoais ou outros achismos. Os cenários a seguir foram criados apenas para tentar estabelcer um paralelo entre a probabilidade de se obter médias amostrais muito destoantes da média populacional e uma “inclinação subjetiva” em se rejeitar uma afirmação.

Considere que a sua amostra em particular é uma das que não se afasta tanto do valor que lhe afirmaram (a vida útil das lâmpadas é de 1.600 h).

Nessa situação, talvez você não se “convencesse” de que a vida útil média fosse diferente daquilo que lhe informaram e, assim, não iria recusar a afirmação.

Agora considere que a sua amostra em particular é uma das que se afasta muito do valor que lhe afirmaram.

Nessa nova situação, certamente você iria “suspeitar” que a vida útil média é diferente daquilo que lhe informaram e assim, recusar a afirmação.

Na primeira decisão, você não recusou uma afirmação que era, de fato, verdadeira; ao passo que na segunda, você rejeitou uma afirmação que era verdadeira (lembrando que você não sabia que a vida útil média é, de fato, 1.600 h).

Como se vê no quadro abaixo, há dois tipos de erros envolvidos em um teste de hipóteses e suas consequências, muitas vezes, são bem diferentes.

Erro do tipo I e
Erro do tipo II.

Um erro do tipo I ocorre quando o pesquisador rejeita uma hipótese nula quando é verdadeira. A probabilidade (limitada pelo pesquisador) de se incorrer em um erro do tipo I é chamada de nível de significância e é frequentemente denotada pela letra grega $\alpha$.

Um erro do tipo II ocorre quando o pesquisador não rejeita uma hipótese nula que é falsa. A probabilidade de cometer um erro do tipo II, também chamada de poder do teste e é frequentemente denotada pela letra grega $\beta$.

Erros envolvidos na rejeição ou não da hipótese nula
Valor real do parâmetro	Não rejeitar	Rejeitar
(desconhecido)	H₀	H₀

H₀ verdadeira	Decisão correta	Erro do tipo I
	probabilidade associada=(1 − α)	probabilidade associada= α
H₀ falsa	Erro do tipo II	Decisão correta
	probabilidade associada=β	probabilidade associada =(1 − β)

No quadro acima identificam-se:

$\alpha$: a probabilidade associada ao cometimento de um erro do tipo I: rejeitar a hipótese nula sendo ela verdadeira (arbitrado pelo pesquisador, é denominado nível de significância do teste);
$\beta$: a probabilidade associada ao cometimento de um erro do tipo II: não rejeitar a hipótese nula sendo esta falsa;
(1-$\alpha$): o nível de confiança estabelecido para a decisão, a probabilidade associada em não se rejeitar a hipótese nula ($H_{0}$) quando ela é, de fato, verdadeira; e,
(1-$\beta$): o poder do teste, a probabilidade associada em não se aceitar a hipótese nula ($H_{0}$) quando ela é, de fato, falsa.

Qual erro é o pior?

Por exemplo, se alguém testa a presença de alguma doença em um paciente, decidindo incorretamente sobre a necessidade do tratamento (ou seja, decidindo que a pessoa está doente), pode submetê-lo ao desconforto pelo tratamento (efeitos colaterais) além de perda financeira pela despesa incorrida.

Mas por outro lado, a falha em diagnosticar a presença da doença no paciente pode levá-lo à morte pela ausência de tratamento.

Outro exemplo clássico a ser citado seria o de condenar uma pessoa inocente ou libertar um criminoso.

Como não há uma regra clara sobre qual tipo de erro é o pior recomenda-se quando se usa dados para testar uma hipótese observar com muito cuidado as consequências que podem seguir os dois tipos de erros. Vários especialistas sugerem o uso de uma tabela como a abaixo para detalhar as consequências de um erro Tipo 1 e Tipo 2 em sua análise específica.

Consequências da tomada de decisão face aos erro envolvidos
H₀ explicada	Erro tipo 1: rejeitar H₀ quando verdadeira	Erro tipo II: não rejeitar H₀ quando falsa
O medicamento “A“ não alivia a Condição “B“	O medicamento “A“ não alivia a Condição “B“, mas não é eliminado como opção de tratamento	O medicamento “A“ alivia a condição “B“, mas é eliminado como opção de tratamento
Consequências	Pacientes com Condição “B“ que recebem o Medicamento “A“ não obtêm alívio. Eles podem experimentar piora da condição e/ou efeitos colaterais, até e incluindo a morte. A empresa produtora do medicamento pode enfrentar processos judiciais	Um tratamento viável permanece indisponível para pacientes com Condição “B“. Os custos de desenvolvimento são perdidos. O potencial lucro pela produção do medicamente “A“ pela empresa é eliminado.

É desejável conduzir o teste de um modo a manter a probabilidade de ambos os tipos de erro em um mínimo.

aumentar o tamanho amostral reduz a probabilidade associada ao cometimento de erro do tipo II ($\beta$) e, consequentemente, aumenta o poder do teste ($1- \beta$);
aumentar o nível de significância ($\alpha$) tem implicação direta na probabilidade associada ao cometimento de erro do tipo I todavia reduz a probabilidade associada ao cometimento de erro do tipo II ($\beta$).