12.4 Coeficiente de correlação linear de Pearson
O mais importante aspecto da correlação linear é a medida de sua intensidade, expressa pelo coeficiente de correlação linear (ou coeficiente de correlação produto momento de Pearson).

Cálculo do coeficiente de correlação amostral \(r\):
\[r = \frac{\sum _{i=1}^{n}{x}_{i} \cdot {y}_{i} - \frac{\sum _{i=1}^{n}{x}_{i}\sum _{i=1}^{n}{y}_{i}}{n}}{\sqrt{\left(\sum _{i=1}^{n}{x}_{i}^{2}-\frac{{\left(\sum _{i=1}^{n}{x}_{i}\right)}^{2}}{n}\right)\cdot \left[\sum_{i=1}^{n}{y}_{i}^{2}-\frac{{\left(\sum _{i=1}^{n}{y}_{i}\right)}^{2}}{n}\right]}}\]
em que \(x_{i}\): é o iésimo valor observado da variável X, \(y_{i}\): é o iésimo valor observado da variável Y, \(n\) é o número de pares de valores observados.
Ou, simplificadamente:
\[ r = \frac{{s}_{xy}}{\sqrt{{s}_{xx}\cdot {s}_{yy}}} \]
em que \(S_{xy} = \sum _{i=1}^{n} x_{i}y_{i}\) - \(\frac{\sum _{i=1}^{n}x_{i}\cdot\sum _{i=1}^{n}y_{i}}{n}\), \(S_{xx} = \sum _{i=1}^{n} x_{i}^{2}\) - \(\frac{(\sum _{i=1}^{n} x_{i})^{2}}{n}\), \({S}_{yy}=\sum _{i=1}^{n}y_{i}^{2}\) - \(\frac{(\sum _{i=1}^{n} y_{i})^{2}}{n}\) e \(n\) é o número de pares de valores observados.
o coeficiente de correlação linear de Pearson tem uma faixa limitada de variação: \(-1 \le r \le 1\),
é simétrico; isto é, a correlação linear observada entre \(X\) e \(Y\) é a mesma que a medida entre as variáveis \(Y\) e \(X\),
é apenas uma medida da associação linear entre duas variáveis e, portanto, não tem sentido usá-lo na quantificação de relações que não o sejam,
a possibilidade de uma correlação linear negativa virá do resultado do numerador (\(S_{xy}\)), pois no denominador temos duas somas de quadrados,
o coeficiente de correlação mede apenas a intensidade das relações lineares entre \(x\) e \(y\) e não estabelece per si nenhuma relação de causação.
- se \(r>0\) dizemos que há uma relação linear positiva entre as variáveis estudadas: para um incremento na primeira variável observa-se também um incremento na segunda;
- se \(r<0\) a relação linear é negativa: um incremento em uma das variáveis é acompanhado por um decremento na outra; e,
- se \(r=0\), então não há uma relação linear entre as variáveis consideradas.
O cálculo do coeficiente de correlação linear de Pearson assemelha-se a uma análise de variância
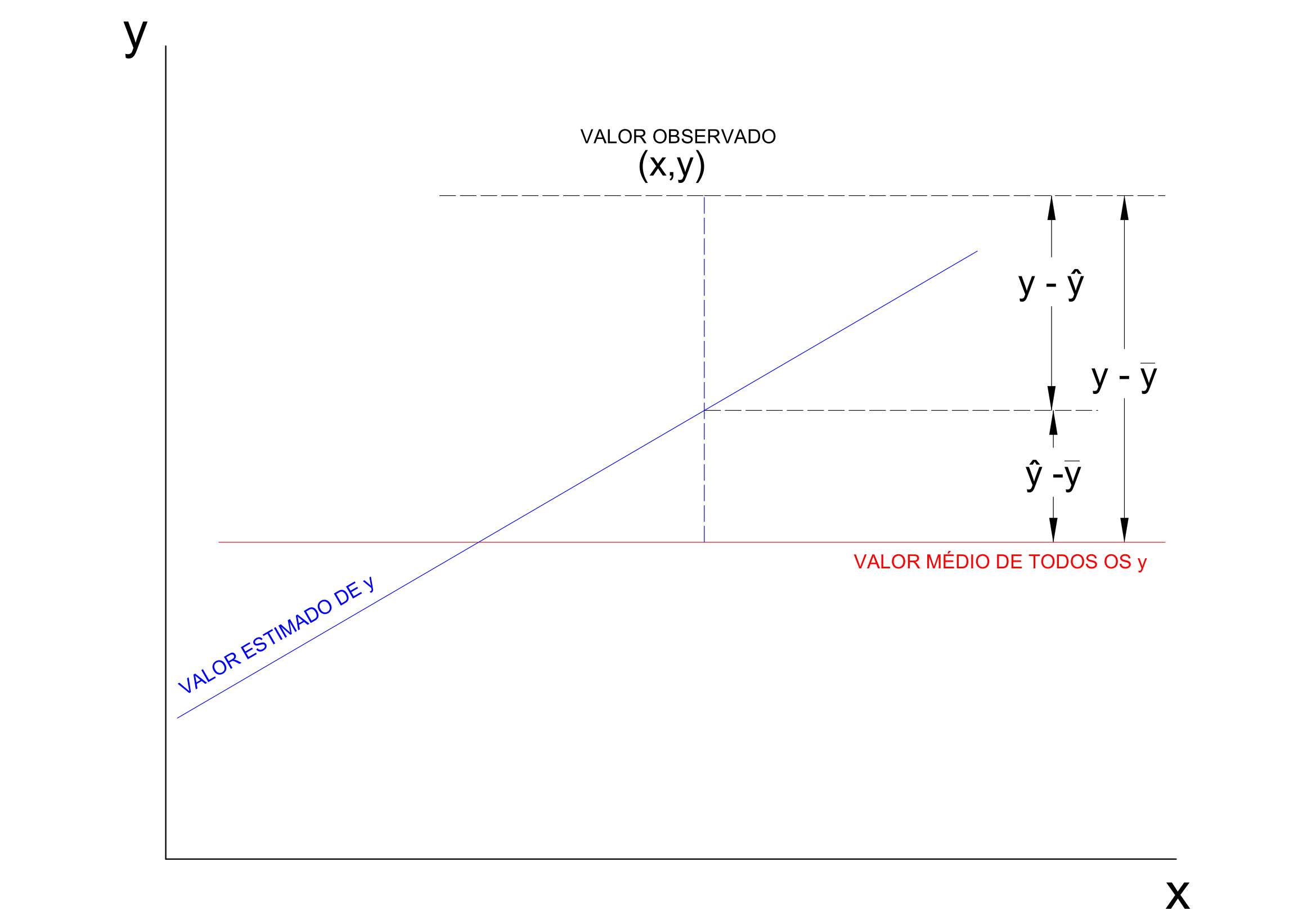
\[ y - \stackrel{-}{y} = (\hat{y} - \stackrel{-}{y}) + (y - \hat{y}) \]
Elevando-se ao quadrado ambos os termos, para todos os valores observados, teremos:
\[ \sum _{i=1}^{n} ({y_{i}} - \stackrel{-}{y_{i}})^{2} = \sum _{i=1}^{n} (\hat{y_{i}} - \stackrel{-}{y_{i}})^{2} + \sum _{i=1}^{n} (y_{i} - \hat{y_{i}})^{2} \]
A quantidade à esquerda mede a variação total dos y (Soma de quadrados total); à direita temos a Soma de quadrados da regressão e a Soma de quadrados dos resíduos e,
\[ r=\sqrt{\frac{\sum _{i=1}^{n} (\hat{y_{i}} - \stackrel{-}{y_{i}})^{2}}{\sum _{i=1}^{n} ({y_{i}} - \stackrel{-}{y_{i}})^{2}}} \]
A definição acima de \(r\) nos diz que \(100.r^{2}\) é a percentagem da variação total dos \(y\) que está sendo explicada por sua regressão linear com \(x\).
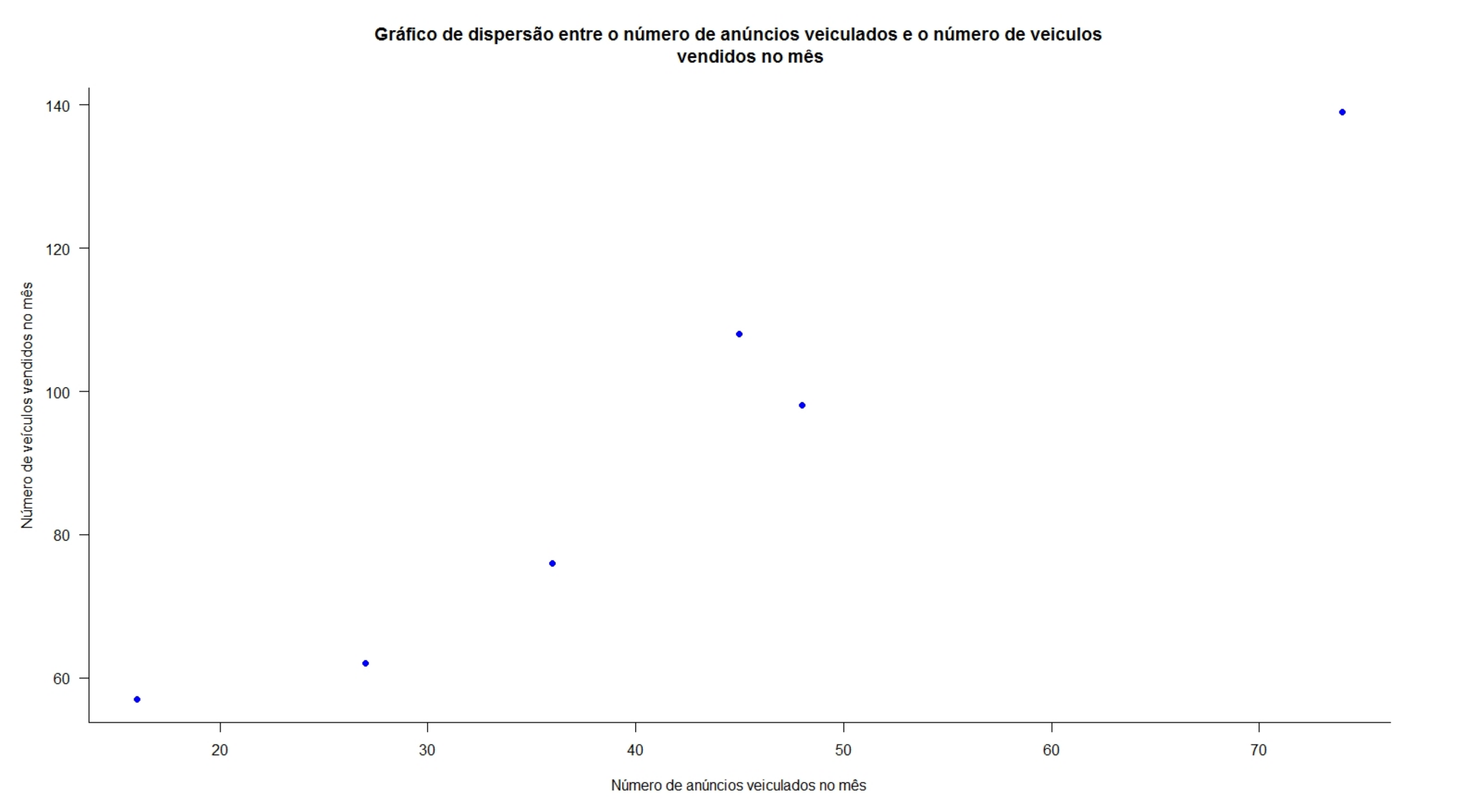
Exemplo 1: Um jornal deseja verificar a eficácia de seus anúncios na venda de carros usados e para isso realizou um levantamento de todos os seus anúncios e informações dos resultados obtidos pelas empresas que o contrataram e dele extraiu uma pequena amostra. A tabela a seguir mostra o número de anúncios e o correspondente número de veículos vendidos por 6 companhias que usaram apenas este jornal como veículo de propaganda. Existe alguma relação linear entre as variáveis? Construa o diagrama de dispersão e calcule o coeficiente de correlação linear.
| Companhia | Anúncios feitos (X) | Carros vendidos (Y) |
|---|---|---|
| A | 74 | 139 |
| B | 45 | 108 |
| C | 48 | 98 |
| D | 36 | 76 |
| E | 27 | 62 |
| F | 16 | 57 |
| Companhia | Anúncios (X) | Carros vendidos (Y) | xi * yi | xi2 | yi2 |
|---|---|---|---|---|---|
| A | 74 | 139 | 10286 | 5476 | 19321 |
| B | 45 | 108 | 4860 | 2025 | 11664 |
| C | 48 | 98 | 4704 | 2304 | 9604 |
| D | 36 | 76 | 2736 | 1296 | 5776 |
| E | 27 | 62 | 1674 | 729 | 3844 |
| F | 16 | 57 | 912 | 256 | 3249 |
| Totais | 246 | 540 | 25172 | 12086 | 53458 |
Sendo \(n= 6\) temos:
\[ S_{xy} = \sum _{i=1}^{n} x_{i}y_{i} - \frac{\sum _{i=1}^{n}x_{i}\cdot\sum _{i=1}^{n}y_{i}}{n} = 25172 - \frac{246 \cdot 540}{6} = 3032\\ S_{xx} = \sum _{i=1}^{n} x_{i}^{2} - \frac{(\sum _{i=1}^{n} x_{i})^{2}}{n} = 12086 - \frac{246^2}{6} = 2000\\ {S}_{yy} = \sum _{i=1}^{n}y_{i}^{2} - \frac{(\sum _{i=1}^{n} y_{i})^{2}}{n}= 53458 - \frac{540^2}{6} = 4858 \]
Portanto:
\[ r = \frac{{s}_{xy}}{\sqrt{{s}_{xx}\cdot {s}_{yy}}} = \frac{3032}{\sqrt{2000 \cdot 4858}} = 0,9727 \]