4.4 Probabilidade de eventos condicionados
Admita dois eventos definidos sobre o exprimento aleatório de se sortear uma carta de um baralho:
- \(A: \{A, 2,3,4,5,6,7,8,9,10,J,Q,K\}_{vermelho}\): cartas vermelhas (ouro e copas), e
- \(B: \{A, J, Q, K\}_{qualquer}\): cartas com figuras.
Se nosso interesse é agora determinar a probabilidade de um evento definido como uma vermelha e de figura ao mesmo tempo ou seja, uma carta que está simultaneamente nos conjuntos \(A\) e \(B\), estamos então interessados na probabilidade da interseção (conectivo \(\cap\)) desses dois eventos: \(P(A \cap B)\). Esse evento (interseção) acaba impondo restrições no espaço amostral inicial (todas as 52 cartas do baralho)
- Olhando-se por um prisma, podemos considerar que o espaço amostral agora é reduzido para \(A\): apenas as 26 cartas vermelhas: copas e ouro e, dentro desse novo espaço amostral, estamos interessados nos elementos \(B\): apenas as 4 cartas de figura: A, J, Q ou K.
A probabilidade do um evento \(B\) condicionada à ocorrência prévia do evento \(A\), pode ser entendida como a fração de \(B\) dentro de \(A\), ou seja:
\[ P(\text{foi sorteada uma carta vermelha, sortear-se uma figura})=\\ \frac{ \text{resultados favoráveis (número de cartas de figuras e vermelhas)}}{\text{resultados possíveis (número de cartas vermelhas)}}=\\ \frac{8}{26}=0,3076\\ \]
- Alternativamente, se olharmos por outro prisma, podemos considerar que o espaço amostral agora é reduzido para \(B\): apenas as 16 cartas de figuras e, dentro desse novo espaço amostral, estamos interessados nos elementos \(A\): apenas as 8 cartas vermelhas.
\[ P(\text{foi sorteada uma carta de figura, sortear-se uma carta vermelha})=\\ \frac{ \text{resultados favoráveis (número de cartas vermelhas e com figuras)}}{\text{resultados possíveis (número de cartas de figuras )}}=\\ \frac{8}{16}=0,50\\ \]
Dois eventos quaisquer \(A\) e \(B\) definidos sobre um experimento aleatório são ditos condicionados quando a ocorrência prévia de um deles impõe uma restrição no espaço amostral do segundo, alterando sua probabilidade original do outro. Ocorrência pode ser entendido alternativamente como uma informação adicional trazida a priori ao experimento, e que alterará a incerteza inicial que pairava sobre os possíveis resultados.
A probabilidade de um evento qualquer \(A\) condicionada a um segundo evento \(B\) é representada como \(P(A|B)\).
A barra vertical pode ser “lida” adotando-se termos correlatos que facilitam o entendimento da relação existente, tais como :
- probabilidade de \(A\) posto que ocorreu \(B\);
- probabilidade de \(A\) admitindo-se que ocorreu \(B\);
- probabilidade de \(A\) considerando-se que ocorreu \(B\),
Uma regra geral para o cálculo da probabilidade de dois eventos condicionados pode ser apresentada como:
\[\begin{align*} P(A|B) & = \frac{ P(A\cap B)}{ P(B)} \\ P(B|A) & = \frac{ P(B\cap A)}{ P(A)} \end{align*}\]
para \(P(B)>0\) e \(P(A)>0\) nas expressões acima.
Trazendo-se ao exemplo das cartas de baralho, as probabilidades marginais de aleatoriamente serem sorteadas cartas vermelhas, de figuras e vermelhas e de figuras são:
- uma carta vermelha: \(P(A)=26/52=0,50\)
- uma carta de figura é \(P(B)=16/52=0,3076\).
- uma carta vermelha e de figura é \(P(A \cap B) = 8/52=0,1538\)
\[ P(\text{foi sorteada uma carta vermelha, sortear-se uma figura}) -> P(B|A) =\\ \frac{ P(B\cap A)}{ P(A)}=\\ \frac{0,1538}{0,50}=\\ 0,3076\\ \]
A probabilidade marginal de se sortear uma carta de figura é 0,3076; todavia, com a informação a priori de que a carta sorteada foi uma carta vermelha, não se alterou.
\[ P(\text{foi sorteada uma carta de figura, sortear-se uma carta vermelha}) -> P(A|B) =\\ \frac{ P(A\cap B)}{ P(B)}=\\ \frac{0,1538}{0,3076}=\\ 0,50 \\ \]
Do mesmo modo, a probabilidade marginal de se sortear uma carta vermelha é 0,50; todavia, com a informação a priori de que a carta sorteada foi uma carta de figura, não se alterou.
Se P(B|A)=P(B) (naturalmente P(A|B)=P(A)) dizemos que os eventos A e B não são condicionados.
Exemplo: Consideremos a Tabela 4.3 que apresenta informações cruzadas do sexo dos alunos e seus respectivos cursos. Vamos definir os eventos Fem:sexo feminino e Est: cursar estatística. Como calcular a probabilidade condicionada de nosso evento de interesse P(Fem|Est) (a probabilidade de um aluno aleatoriamente escolhido ser do sexo feminino, dado que ele cursa estatística)?
\[\begin{align*} P(Fem|Est) & = \frac{ P(Fem \cap Est)}{ P(Est)} \\ & = \frac{20}{30} = \frac{2}{3} \end{align*}\]
Esse cálculo é facilmente entendido observando-se as celulas da distribuição de frequências na Tabela 4.3.
Exemplo: Considerem a Tabela 4.4 que relaciona a ida à praia de uma certa pessoa às condições climáticas do dia.
| Dia | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Foi à praia? | N | S | N | S | S | S | N | N | S | S |
| Fez sol? | N | S | N | S | N | S | S | N | S | S |
Baseado nos dados coletados responda:
1- Qual a probabilidade dessa pessoa ir à praia?
2- Sabendo-se que fez Sol, qual a probabilidade dessa pessoa ir à praia?
3- Os eventos ir à praia e fazer Sol são independentes ou condicionados?
Da Tabela 4.4 extraímos as seguintes probabilidades:
\[\begin{align*} P(IP) & = \frac{6}{10}= 0,60 \\ P(FS) & = \frac{6}{10}= 0,60 \\ P(IP \cap FS) & = \frac{5}{10} \\ & = 0,50 \end{align*}\]
A partir delas podemos calcular a seguinte probabilidade condicionada:
\[\begin{align*} P(IP|FS) & = \frac{ P(IP \cap F)}{ P(FS)} \\ & = \frac{5}{6} \\ & = 0,83 \end{align*}\]
A probabilidade dessa pessoa ir à praia (\(P(IP)\)) é 0,60; mas quando faz Sol a probabilidade (\(P(IP|FS)\)) dela aumenta para 0,83.
Assim, os eventos \(IP\) e \(FS\) são condicionados: essa pessoa vai à praia 60% dos dias analisados; mas, quando faz sol, ela vai em 83% dos dias (a presença de Sol altera a probabilidade dela ir à praia).
Exemplo: Em uma cidade existem 15.000 usuários de telefonia, dos quais 10.000 possuem telefones fixos, 8.000 telefones móveis e 3.000 telefones fixos e móveis. Seja o experimento aleatório de uma operadora de telefone móvel selecionar uma pessoa dessa cidade para oferecer uma promoção do tipo “Fale Grátis de seu Móvel para seu Fixo”.
Responda:
1- Sorteando-se aleatoriamente um cliente dessa operadora, se soubermos antecipadamente que ele tem telefone móvel, qual a probabilidade de esse cliente tenha telefone fixo também?
2- Sabendo-se que ele tem telefone fixo, qual a probabilidade de ele tenha telefone móvel também?
O espaço amostral de todos esses possíveis eventos pode ser ilustrado pelo diagrama de Venn abaixo:
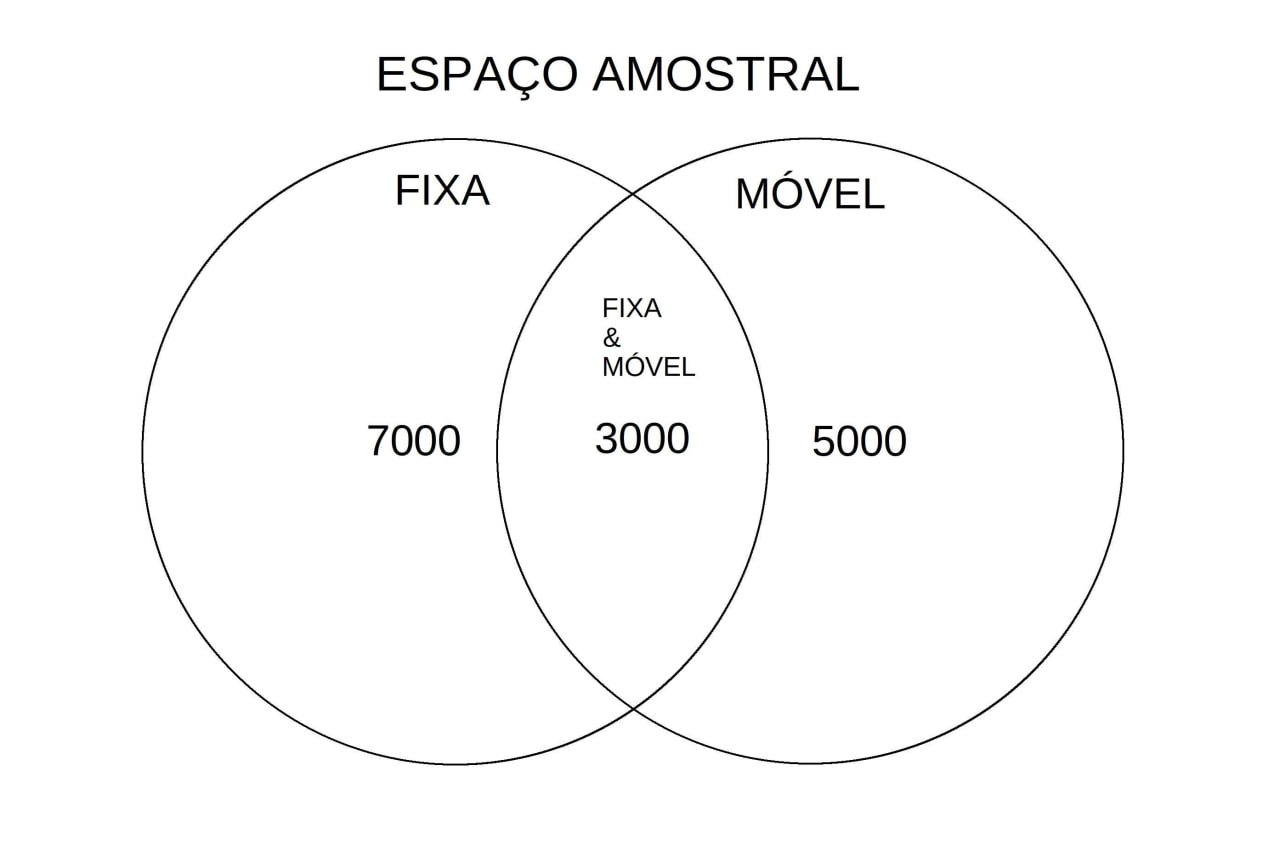
Figure 4.15: Diagrama de Venn do espaço amostral
Do diagrama apresentado na Figura4.15 podemos extrair imediatamente as probabilidades pedidas:
- \(P(F|M)\) (probabilidade de ter uma linha fixa sabendo que possui um telefone móvel); e,
- \(P(M|F)\) (probabilidade de ter uma linha móvel sabendo que possui um telefone fixo):
\[\begin{align*}
P(F|M) & = \frac{n(MF)}{n(M)}\\
& =\frac{3000}{8000}\\
& = 0,375
\end{align*}\]
e
\[\begin{align*} P(M|F) & = \frac{n(MF)}{n(F)} \\ & =\frac{3000}{10000} \\ & = 0,300 \end{align*}\]
Mas também podemos calcular as probablidades do modo como explicado no começo desta sessão. Definindo-se os eventos \(F:\) telefone fixo e \(M:\) telefone móvel, a primeira pergunta pede \(P(F|M)\):probabilidade de ter um telefone fixo sabendo que ele tem um telefone móvel:
\[\begin{align*}
P(F|M) & = \frac{P(F \cap M)}{P(M)} \\
& = \frac{ \frac{3000}{15000} }{\frac{8000}{15000} }\\
& = 0,375.
\end{align*}\]
A segunda pede \(P(M|F)\): probabilidade de ter um telefone móvel sabendo que ele tem um telefone fixo:
\[\begin{align*} P(M|F) & = \frac{P(M \cap F)}{P(F)} \\ & = \frac{ \frac{3000}{15000} }{\frac{10000}{15000} } \\ & = 0,300 \end{align*}\]
Exemplo: Considere a Tabela 4.5 onde são expostos os resultados de uma pesquisa relacionada ao gosto pela prática de tênis entre alunos e alunas. Definindo-se os eventos \(A\):“gostar de tênis” e \(B\):“ser do sexo feminino”, calcule as probabilidade pedidas ao se sortear, aleatoriamente, uma das pessoas pesquisadas.
1- Qual a probabilidade de que goste de tênis (\(P(T)\))?
2- Qual probabilidade de que não goste de tênis (\(P(T^{c})\))?
3- Qual a probabilidade de que seja do sexo feminino ou goste de tênis: (\(P(F \cup T)\))?
4- Sabendo-se que foi sorteada uma aluna, qual a probabilidade de que goste de tênis (\(P(T|F))\)?
5- Verifique se os eventos \(T\): “gostar de tênis” e \(F\):“ser do sexo feminino” são condicionados ou independentes (\(P(T \cap F) \stackrel{?}{=} P(T) \times P(F)\)))
| Sexo | |||
|---|---|---|---|
| Curso | |||
| Masculino (M) | Feminino (F) | Total | |
| Gostam de tênis (T) | 400 | 200 | 600 |
| Não gostam de tênis (NT) | 50 | 50 | 100 |
| Total | 450 | 250 | 700 |
Exemplo: Imagine que um jogador está treinando cobranças de pênaltis. Historicamente a probabilidade de acertar uma cobrança, supondo que acertou a anterior é de 60%. Mas, se ele tiver errado a anterior a probabilidade de acertar cai para 30%. Construa a distribuição de probabilidades do número de acertos em 3 tentativas de cobrança.
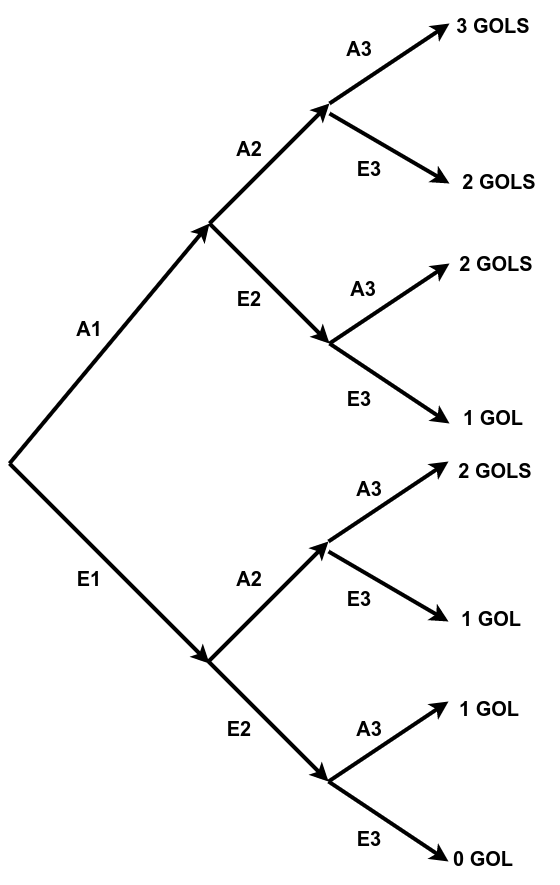
Figure 4.16: Diagrama em árvore das três repetições dependentes de um pênalti
A seguir vemos a cadeia de eventos necessária para que cada contagem de gols se verifique:
\[\begin{align*} \text{0 GOL} & = [E_{1} \cap E_{2} \cap E_{3}] \\ \text{1 GOL} & = \{ [A_{1} \cap E_{2} \cap E_{3}] \cup [E_{1} \cap A_{2} \cap E_{3}] \cup [E_{1} \cap E_{2} \cap A_{3}] \}\\ \text{2 GOLS} & = \{ [A_{1} \cap A_{2} \cap E_{3}] \cup [E_{1} \cap A_{2} \cap A_{3}] \cup [A_{1} \cap E_{2} \cap A_{3}] \}\\ \text{3 GOLS} & = [A_{1} \cap A_{2} \cap A_{3}] \\ \end{align*}\]
A probabilidade associada a cada contagem de gols será:
\[\begin{align*} P(\text{0 GOL}) & = P[E_{1} \cap E_{2} \cap E_{3}] \\ P(\text{1 GOL}) & = P\{ [A_{1} \cap E_{2} \cap E_{3}] \cup [E_{1} \cap A_{2} \cap E_{3}] \cup [E_{1} \cap E_{2} \cap A_{3}] \}\\ P(\text{2 GOLS}) & = P\{ [A_{1} \cap A_{2} \cap E_{3}] \cup [E_{1} \cap A_{2} \cap A_{3}] \cup [A_{1} \cap E_{2} \cap A_{3}] \}\\ P(\text{3 GOLS}) & = P[A_{1} \cap A_{2} \cap A_{3}] \\ \end{align*}\]
A partir do enunciado, podemos deduzir as probabilidades de cada um dos eventos:
\[\begin{align*} P(A_{1}) & = 0,50 \\ P(E_{1}) & = 0,50\\ P(A_{i+1}|A_{i}) & =0,60 \text{ logo, pelo complementar, } P(E_{i+1}|A_{i})=0,40\\ P(A_{i+1}|E_{i}) & =0,30 \text{ logo, pelo complementar } P(E_{i+1}|E_{i})=0,70\\ \end{align*}\]
\[\begin{align*} P(\text{0 GOL}) & = P[E_{1} \cap E_{2} \cap E_{3}] \\ P(\text{0 GOL}) & = P[E_{1}] \times P[E_{2}|E_{1}] \times P[E_{3}|E_{2}] \\ P(\text{0 GOL}) & = 0,50 \times 0,70 \times 0,70 \\ P(\text{0 GOL}) & = 0,245 \end{align*}\]
\[\begin{align*} P(\text{3 GOLS}) & = P[A_{1} \cap A_{2} \cap A_{3}] \\ P(\text{3 GOLS}) & = P[A_{1}] \times P[A_{2}|A_{1}] \times P[A_{3}|A_{2}] \\ P(\text{3 GOLS}) & = 0,50 \times 0,60 \times 0,60 \\ P(\text{3 GOLS}) & = 0,18 \end{align*}\]
\[\begin{align*} P(\text{1 GOL}) & = P\{ [A_{1} \cap E_{2} \cap E_{3}]\} + P\{ [E_{1} \cap A_{2} \cap E_{3}]\} + P\{[E_{1} \cap E_{2} \cap A_{3}]\}\\ P(\text{1 GOL}) & = P[A_{1}] \times P[E_{2}|A_{1}] \times P[E_{3}|E_{2}] +\\ & P[E_{1}] \times P[A_{2}|E_{1}] \times P[E_{3}|A_{2}] +\\ & P[E_{1}] \times P[E_{2}|E_{1}] \times P[A_{3}|E_{2}]\\ P(\text{1 GOL}) & = 0,50 \times 0,40 \times 0,70 +\\ & 0,50 \times 0,30 \times 0,40 +\\ & 0,50 \times 0,70 \times 0,30 \\ P(\text{1 GOL}) & =0,305 \end{align*}\]
\[\begin{align*} P(\text{2 GOLS}) & = P\{ [A_{1} \cap A_{2} \cap E_{3}]\} + P\{ [E_{1} \cap A_{2} \cap A_{3}]\} + P\{[A_{1} \cap E_{2} \cap A_{3}]\}\\ P(\text{2 GOLS}) & = P[A_{1}] \times P[A_{2}|A_{1}] \times P[E_{3}|A_{2}] +\\ & P[E_{1}] \times P[A_{2}|E_{1}] \times P[A_{3}|A_{2}] +\\ & P[A_{1}] \times P[E_{2}|A_{1}] \times P[A_{3}|E_{2}]\\ P(\text{2 GOLS}) & = 0,50 \times 0,60 \times 0,40 +\\ & 0,50 \times 0,30 \times 0,60 +\\ & 0,50 \times 0,40 \times 0,30 \\ P(\text{2 GOLS}) & =0,27 \end{align*}\]