13.4 Processo de Poisson
13.4.1 Natureza
Alguns experimentos aleatórios envolvem, essencialmente, contagens observadas em um certo intervalo de tempo como, por exemplo:
1- clientes que entram num supermercado por dia, 2- chamadas que uma central telefônica recebe por hora,
3. pacotes que passam por um roteador por minuto,
4. chamadas ao SIATE por semana,
5. trens que chegam a uma estação a cada 12 horas.
Ao se aumentar o intervalo, aumenta-se a probabilidade de se observar uma certa contagem.
Definição 1: um processo de contagem é um processo estocástico temporal representado por: \[ \{N_t : t \in [0, \infty) \} \] em que: \(N_t\) representa o número de eventos ocorridos no intervalo [0, t].
Esse processo deve satisfazer as seguintes propriedades:
- \(N_0 = 0\) (no exato momento do início do processo a contagem é zero)
- \(N_t \in \{0, 1, 2, \ldots \}\) (\(ie\), são contagens)
- Se \(s < t\), então \(N_s \leq N_t\) (a contagem no intervalo [0,s] não é superior à contagem no intervalo [0,t], para \(s < t\))
- Para \(s < t\), a diferença \(N_t - N_s\) representa o número de eventos ocorridos no intervalo \((s, t]\)
- \(N_t\) é uma função não descrescente
Definição 2: um processo de contagem tem incrementos independentes se o número de eventos que ocorrem em intervalos de tempo disjuntos são independentes. Para \(0 \leq t_1 < t_2 < \ldots < t_n\), temos que as variáveis aleatórias: \[ N(t_2) - N(t_1), N(t_3) - N(t_2), \ldots, N(t_n) - N(t_{n-1}) \] são variáveis independentes.
Definição 3: um processo de contagem tem incrementos estacionários se a distribuição de probabilidade do número de eventos que ocorrem em qualquer intervalo é a mesma e depende apenas da duração do intervalo (a probabilidade de chegar um cliente entre 9 e 10 h é a mesma de chegar um cliente entre 15 e 16 h: \(P(N([9,10])=P(N([15,16])\)): falta de memória

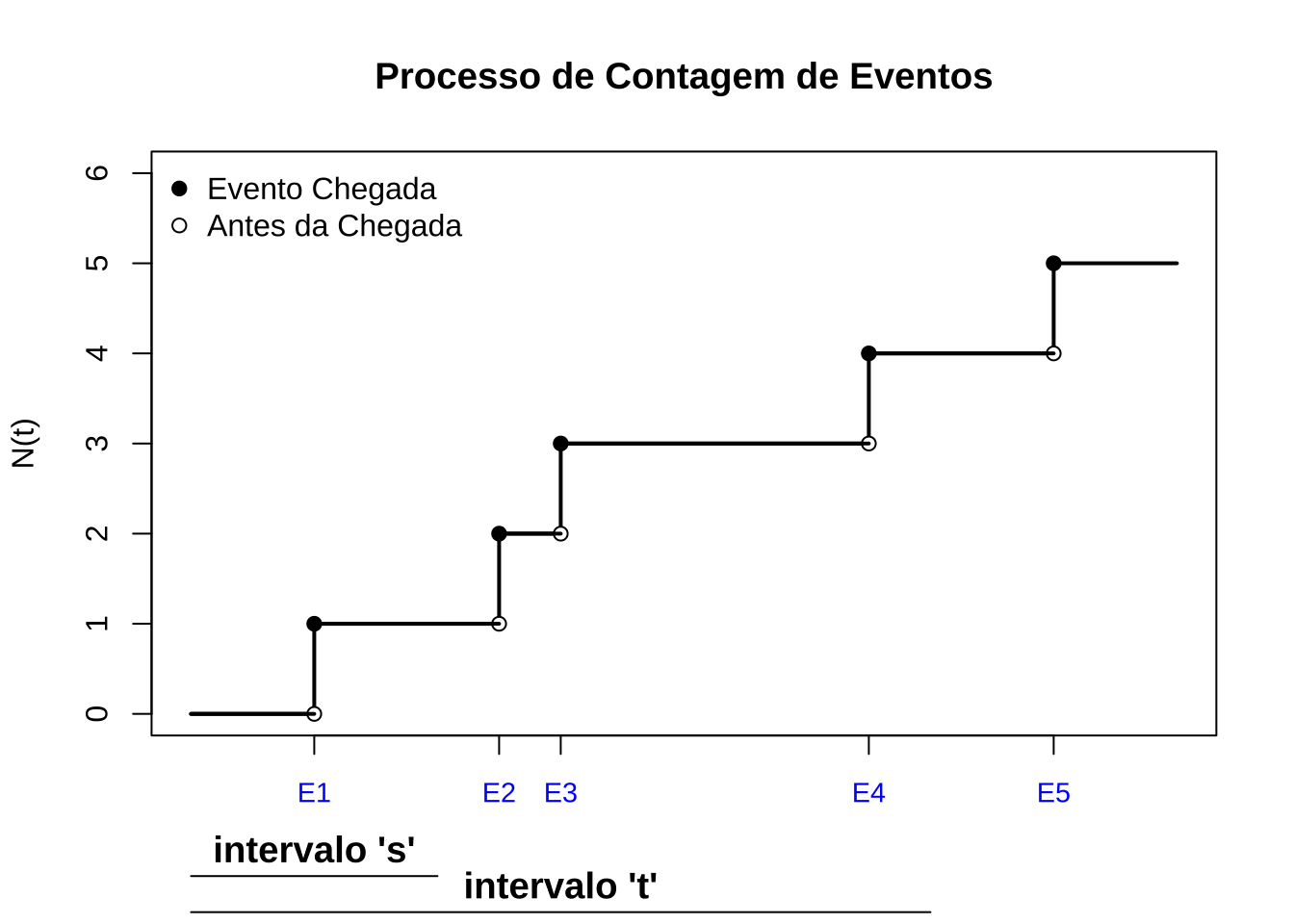
Figure 13.1: O processo de Poisson: (1) tem contagem zero em t=0; (2) se s<t então N(s)<N(t); (4) N(t) é não descrescente e (4) os incrementos são independentes
Um processo de contagem \(\{N_t : t \geq 0 \}\) é dito ser um processo de Poisson com taxa \(\lambda > 0\) se:
- \(N(0) = 0\).
- o processo tem incrementos independentes e estacionários.
- o número de eventos em qualquer intervalo de comprimento \(t\) tem distribuição de Poisson com média \(\lambda t\).
Ou seja, para \(s, t \geq 0\)
\[ P(N(t + s) - N(s) = n) = \frac{e^{-\lambda t} (\lambda t)^n}{n!} \]
em que \(P(N(t + s) - N(s) = n)\) é a probabilidade de serem observados \(n\) eventos no intervalo de tempo \((t+s)-t=t\). Desse modo, para um intervalo de tempo \(t\), a probabilidade de serem observados \(n\) eventos é
\[ P(N(t) = n) = \frac{e^{-\lambda t} (\lambda t)^n}{n!} \]
Exemplo 1: Fregueses chegam a uma certa loja de acordo com um processo de Poisson com taxa \(\lambda = 4\) fregueses por hora. Admita que a loja abra às 9h e que que os fregueses não deixam a loja. Quais são as probabilidades de que: 1. um freguês chegue até às 9:30h
2. um total de 5 fregueses estejam na loja até às 11:30h?
A loja abre às 9 h então até as 9 h 30 min o primeiro intervalo de tempo será \(t_1 = 0.5\) horas e até as 11 h 30 min o segundo intervalode tempo será \(t_2 = 2.5\). A taxa média de chegadas por hora é \(\lambda = 4\).
O que se pede é a \(P[N(t_1)=1,N(t_2)=5]\).
Essa probabilidade é a mesma que \(P[N(t_1)=1 \cap N(t_2-t_1)=4]\) e, sendo os intervalos de tempo disjuntos, as probabilidades \(P[N(t_1)=1]\) e \(P[N(t_2 - t_1)=4]\) são independentes e podemos escrever:
\[\begin{align} P[N(t_1)=1 \cap N(t_2-t_1)=4] & = P[N(t_1)=1] \times P[N(t_2-t_1)=4] \\ & = \frac{\varepsilon^{-\lambda t_1} (\lambda t_1)^{n_1}}{n_1!} \times \frac{\varepsilon^{-\lambda (t_2-t_1)}[\lambda (t_2-t_1)]^{n_2}}{n_2!}\\ & = \frac{\varepsilon^{-(4\times 0.5)} (4 \times 0.5)^{1}}{1!} \times \frac{\varepsilon^{-(4 \times 2)} (4 \times 2)^{4}}{4!}\\ & = 2\varepsilon^{-2} \times 170.67\varepsilon^{-8}\\ & = 0.2707 \times 0.0573 \approx 0.0155 \end{align}\]
Um valor bastante baixo posto a taxa média \(\lambda\) de 4 clientes por hora indicar que se esperam 2 em meia hora (apenas 1 chegou) e 8 em duas horas (apenas 4 chegaram). Ambos os eventos: chegar 1 pessoa em meia hora e 4 pessoas em duas horas são raros.
Exemplo 2: Suponha que pacotes SMTP chegam a um servidor de e-mails de acordo com um processo de Poisson com frequência \(\lambda = 2\) pacotes por segundo. Seja \(N(t)\) o número de mensagens que chegam até o tempo \(t\). Quais são as probabilidades de que: 1. \(P(N(1) = 2)\): 2 pacotes em um intervalo de 1 segundo
2. \(P(N(1) = 2 \cap N(3) = 6)\): 2 pacotes em um intervalo de 1 segundo e 6 pacotes em um intervalo de 3 segundos 3. \(P(N(1) = 2 | N(3) = 6)\) 4. \(P(N(3) = 6 | N(1) = 2)\)
A primeira probabilidade é imediata:
\[\begin{align} P(N(1) = 2) & = \frac{e^{-2 \times 1} (2 \times 1)^2}{2!}\\ & = \frac{e^{-2} \cdot 4}{2} \\ & = 2 e^{-2} \approx 0.27 \end{align}\]
A segunda,recorrendo à mesma definição do exemplo anterior, será dada por:
\[\begin{align} P[N(1)=2 \cap N(3)=6] & = P[N(1)=2] \times P[N(2)=4] \\ & = \frac{\varepsilon^{-(2\times 1)} (2 \times 1)^{2}}{2!} \times \frac{\varepsilon^{-(2 \times 2)} (2 \times 2 )^{4}}{4!}\\ & = 0.2707 \times 0.1952 \approx 0.052 \end{align}\]
A terceira, recorrendo à probabilidade de dois eventos condicionado \(P(A|B)=\frac{P(A\cap B)}{P(B)}\), será dada por:
\[\begin{align} P(N(1) = 2 | N(3) = 6) & = \frac{P(N(1) = 2 \cap N(3) = 6)}{P(N(3) = 6)}\\ & = \frac{0.052}{P(N(3) = 6)}\\ & = \frac{0.052}{0.1606} \approx 0.32 \\ \end{align}\]
A quarta podemos entender que a probabilidade de N(3)=6 dado N(1) = 2, ilustrada a seguir:
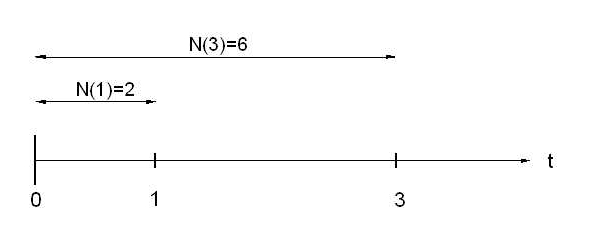
Portanto, calcular \(P(N(3) = 6 | N(1) = 2)\) equivale a calcular a probabilidade de \(P(N(2)=4)\) (os incrementos são independentes em um processo de Poisson), dada por \(\frac{\varepsilon^{-(2\times 2)} (2 \times 2)^{4}}{4!} \approx 0.19\) .
13.4.2 Processo de Poisson com classificação de eventos
Seja \(\{N(t), t \geq 0\}\) um processo de Poisson com taxa \(\lambda\), que descreve o número de eventos ocorridos em um intervalo de tempo \([0, t]\). Admita que cada evento nesse processo possa ser classificado em dois tipos distintos (Tipo I e Tipo II):
- Cada evento tem probabilidade \(p\) de ser classificado como Tipo I.
- Cada evento tem probabilidade \(1-p\) de ser classificado como Tipo II.
Se a classificação de cada evento é independente das demais classificações e da ocorrência dos eventos, demonstra-se (Sheldon Ross, in Introduction to Probability Models, \(6^{a}\) ed., Cap. 5) que
- \(\{N_1(t), t \geq 0\}\): Número de eventos do Tipo I no intervalo \([0, t]\).
- \(\{N_2(t), t \geq 0\}\): Número de eventos do Tipo II no intervalo \([0, t]\),
e \(N(t) = N_1(t) + N_2(t)\).
Os processos \(\{N_1(t), t \geq 0\}\) e \(\{N_2(t), t \geq 0\}\) têm as seguintes propriedades:
1. Ambos são processos de Poisson com taxas:
- \(\lambda_1 = \lambda p\) para eventos do Tipo I.
- \(\lambda_2 = \lambda (1-p)\) para eventos do Tipo II.
2. Os dois processos são independentes.
\[ N_1(t) \sim \text{Poisson}(\lambda p), \quad N_2(t) \sim \text{Poisson}(\lambda (1-p)) \]
De modo geral, considere um processo de Poisson com taxa \(\lambda\). Cada evento pode ser classificado em n tipos diferentes com probabilidades:
\[ p_1, p_2, \ldots, p_n, \quad p_1 + p_2 + \cdots + p_n = 1 \]
Seja \(N_i(t)\) o número de eventos do tipo \(i\) até o tempo \(t\).Cada subprocesso segue uma distribuição de Poisson com taxa:
\[ N_i(t) \sim \text{Poisson}(p_i \lambda t) \]
Os subprocessos \(N_1(t), N_2(t), \ldots, N_n(t)\) são independentes entre si.
A ocorrência de um evento de um tipo não afeta a probabilidade de ocorrência de eventos de outro tipo.
Cada tipo de evento mantém suas próprias propriedades estatísticas e comportamentos, preservando a estrutura probabilística do processo original.
A proposição afirma que podemos decompor um processo de Poisson subprocessos independentes, onde cada subprocesso segue uma distribuição de Poisson ajustada pela probabilidade de classificação de cada evento.
Esse resultado é frequentemente utilizado em aplicações práticas, como: filas com diferentes tipos de clientes e sistemas de telecomunicações com pacotes de dados de diferentes tipos.
Exemplo 3: Clientes entram em uma loja de acordo com um processo de Poisson com taxa λ = 10 por hora. De forma independente, cada cliente compra alguma coisa com probabilidade 0.3 ou sai da loja sem comprar nada com probabilidade 0.7. Calcule a probabilidade de que durante a primeira hora 9 pessoas entrem na loja e, dentre essas 9 pessoas, 3 comprem alguma coisa e 6 não.
Considerando que \(N_0(t)\) e \(N_1(t)\) são processos de Poisson independentes com taxas \((1 − p)\lambda\) e \(p \lambda\), em que \(N_0(t)\) o número de clientes que não compram nada até o tempo \(t\) e \(N_1(t)\) o número de clientes que compram até o tempo \(t\), a probabilidade pedida é
\[ P(N_0(t=1)=6, N_1(t=1)=3)\]
em que \(N_0(t=1) \sim Poisson(\lambda_0=7)\) e \(N_1(t=1) \sim Poisson(\lambda_1=3)\).
\[\begin{align} P(N_0(t=1)=6 \land N_1(t=1)=3) & = P(N_0(t=1)=6) \times P(N_1(t=1)=3)\\ & = \frac{e^{-\lambda_0 t} (\lambda_0 t)^n_0}{n_0!} \times \frac{e^{-\lambda_1 t} (\lambda_1 t)^n_1}{n_1!} \\ & = \frac{e^{-7 \times 1}\dot(7 \times 1)^6}{6!} \times \frac{e^{-3 \times 1}\dot(3 \times 1)^3}{3!} \\ & \approx 0.1251 \times 0.2666 \\ & \approx 0.0333 \end{align}\]
13.4.4 Tempo de espera em um processo de Poisson
Seja \(\{N_t : t \geq 0 \}\) um processo de Poisson com taxa \(\lambda\):
- denota-se por \(T_{n}\) o tempo entre a \((n − 1)\) e a \(n-ésima\) ocorrência de eventos, sendo \(T_{1}\) o tempo até a primeira ocorrência
- a sequência \(T_{n}, n=1,2,...\) é a chamada sequência de tempos entre ocorrências (ou entre chagadas)
Proposição: \(T_{1},T_{2},...\) são variáveis aleatórias com distribuição exponencial de parâmetro \(\frac{1}{\lambda}\).
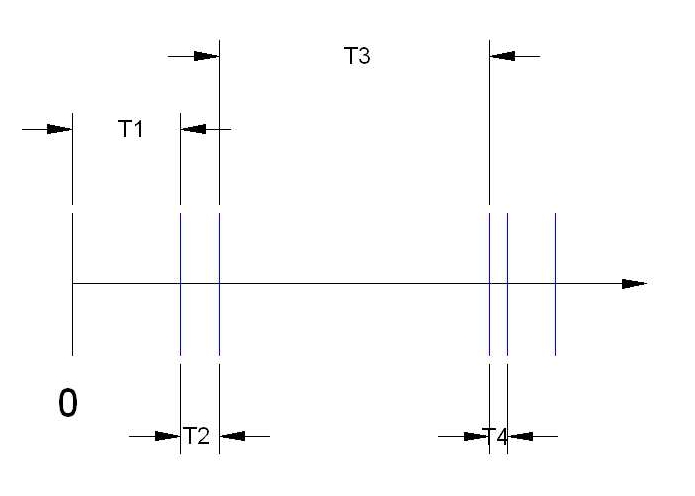
Figure 13.2: Os tempos de espera entre cada observação não são constantes.
import numpy as np
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
from scipy.stats import expon
#A função **`generate_poisson_events`** simula um **Processo de Poisson**, gerando um número aleatório de eventos com taxa média `rate` em um intervalo de duração `time_duration`, retornando o número total de eventos, os tempos ordenados de ocorrência e os intervalos entre eventos consecutivos.
def generate_poisson_events(rate, time_duration):
num_events = np.random.poisson(rate * time_duration)
event_times = np.sort(np.random.uniform(0, time_duration, num_events))
inter_arrival_times = np.diff(event_times)
return num_events, event_times, inter_arrival_times
# A função **`plot_non_sequential_poisson`** visualiza um **Processo de Poisson**, exibindo em dois gráficos o tempo cumulativo dos eventos (em uma curva de passos) e o histograma dos intervalos entre eventos, destacando a distribuição exponencial dos tempos de espera, com taxa média `rate` e duração total `time_duration`.
def plot_non_sequential_poisson(num_events, event_times, inter_arrival_times, rate, time_duration):
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
fig.suptitle(f'Simulação de um Processo de Poisson (λ = {rate}, Duração = {time_duration} segundos)\n', fontsize=14)
# Gráfico 1: Tempo dos Eventos
axs[0].step(event_times, np.arange(1, num_events + 1), where='post', color='blue')
axs[0].set_xlabel('Tempo (s)')
axs[0].set_ylabel('Número de Eventos')
axs[0].set_title(f'Evolução Incremental dos Eventos no Tempo\nN(t) é não descrescente\nTotal: {num_events} eventos\n', fontsize=12)
axs[0].grid(True)
# Gráfico 2: Histograma dos Tempos de Espera
axs[1].hist(inter_arrival_times, bins=20, density=True, color='green', alpha=0.5, label='Dados Empíricos')
axs[1].set_xlabel('Tempo de Espera entre Eventos (s)')
axs[1].set_ylabel('Densidade')
axs[1].set_title(
f'Distribuição dos Tempos de Espera entre Eventos\nE(T): {1/rate:.2f}, Sd(T): {np.std(inter_arrival_times):.2f}',
fontsize=12
)
axs[1].grid(True, alpha=0.5)
# Sobreposição da curva exponencial teórica
lambda_param = rate
x = np.linspace(0, max(inter_arrival_times), 100)
y = expon.pdf(x, scale=1/lambda_param)
axs[1].plot(x, y, 'r-', lw=2, label=f'Modelo Exponencial (λ={lambda_param:.2f})')
# Legenda
axs[1].legend()
# Ajustar espaçamento entre gráficos
plt.subplots_adjust(left=0.08, right=0.95, top=0.85, bottom=0.1, wspace=0.3)
# Ajustar layout final
plt.tight_layout()
plt.show()
# A função **`plot_sequential_poisson`** visualiza múltiplos **Processos de Poisson** com diferentes taxas `rate`, exibindo em dois gráficos a evolução cumulativa dos eventos no tempo e os histogramas dos intervalos entre eventos, destacando a distribuição exponencial dos tempos de espera para cada taxa ao longo de uma duração definida `time_duration`.
def plot_sequential_poisson(num_events_list, event_times_list, inter_arrival_times_list, rate, time_duration):
fig, axs = plt.subplots(1, 2, figsize=(14, 5))
fig.suptitle(f'Simulação de Processos de Poisson com diferentes λ (Duração = {time_duration} segundos)\n', fontsize=14)
# Gráfico 1: Tempo dos Eventos
axs[0].set_xlabel('Tempo (s)')
axs[0].set_ylabel('Número de Eventos')
axs[0].set_title(f'Evolução Incremental dos Eventos no Tempo \nN(t) é não decrescente', fontsize=12)
axs[0].grid(True)
# Gráfico 2: Histograma dos Tempos de Espera
axs[1].set_xlabel('Tempo de Espera entre Eventos (s)')
axs[1].set_ylabel('Densidade')
axs[1].set_title(f'Distribuição dos Tempos de Espera: T(n) ~ Exp\n E(T)=1/λ, Sd(T)=sqrt(1/λ²)', fontsize=12)
axs[1].grid(True, alpha=0.5)
color_palette = plt.get_cmap('tab20')
colors = [color_palette(i) for i in range(len(rate))]
for n, individual_rate in enumerate(rate):
num_events = num_events_list[n]
event_times = event_times_list[n]
inter_arrival_times = inter_arrival_times_list[n]
# Gráfico 1: Curva de passos para os tempos de chegada
axs[0].step(event_times, np.arange(1, num_events + 1), where='post', color=colors[n],
label=f'λ = {individual_rate}, Total: {num_events}')
# Gráfico 2: Histograma dos tempos entre eventos
axs[1].hist(inter_arrival_times, bins=20, density=True, color=colors[n], alpha=0.5,
label=f'λ = {individual_rate}, E(T): {1/individual_rate:.2f}, Sd(T): {np.std(inter_arrival_times):.2f}')
# Sobreposição da curva exponencial teórica
x = np.linspace(0, max(inter_arrival_times), 100)
y = expon.pdf(x, scale=1/individual_rate)
axs[1].plot(x, y, color=colors[n], lw=2, linestyle='--', label=f'Modelo Exp (λ={individual_rate:.2f})')
axs[0].legend(loc='upper left', fontsize=9)
axs[1].legend(loc='upper right', fontsize=9)
# Ajustar espaçamento entre gráficos
plt.subplots_adjust(left=0.08, right=0.95, top=0.85, bottom=0.1, wspace=0.3)
# Ajustar layout final
plt.tight_layout()
plt.show()
# A função **`poisson_simulation`** simula um ou vários **Processos de Poisson**, dependendo se `rate` é um valor único (int) ou uma lista de taxas, gerando tempos de ocorrência e intervalos entre eventos; além disso, visualiza os resultados por meio de gráficos que exibem a evolução temporal dos eventos e a distribuição dos tempos de espera ao longo de um intervalo definido por `time_duration`.
def poisson_simulation(rate, time_duration, show_visualization=True):
if isinstance(rate, int):
num_events, event_times, inter_arrival_times = generate_poisson_events(rate, time_duration)
if show_visualization:
fig = plt.figure(figsize=(14, 6)) # Aumentar tamanho da figura
plot_non_sequential_poisson(num_events, event_times, inter_arrival_times, rate, time_duration)
fig.set_tight_layout(True) # Ajuste automático do layout
else:
return num_events, event_times, inter_arrival_times
elif isinstance(rate, list):
num_events_list = []
event_times_list = []
inter_arrival_times_list = []
for individual_rate in rate:
num_events, event_times, inter_arrival_times = generate_poisson_events(individual_rate, time_duration)
num_events_list.append(num_events)
event_times_list.append(event_times)
inter_arrival_times_list.append(inter_arrival_times)
if show_visualization:
fig = plt.figure(figsize=(18, 8)) # Maior espaço para gráficos sequenciais
plot_sequential_poisson(num_events_list, event_times_list, inter_arrival_times_list, rate, time_duration)
fig.set_tight_layout(True) # Ajuste automático do layout
else:
return num_events_list, event_times_list, inter_arrival_times_list
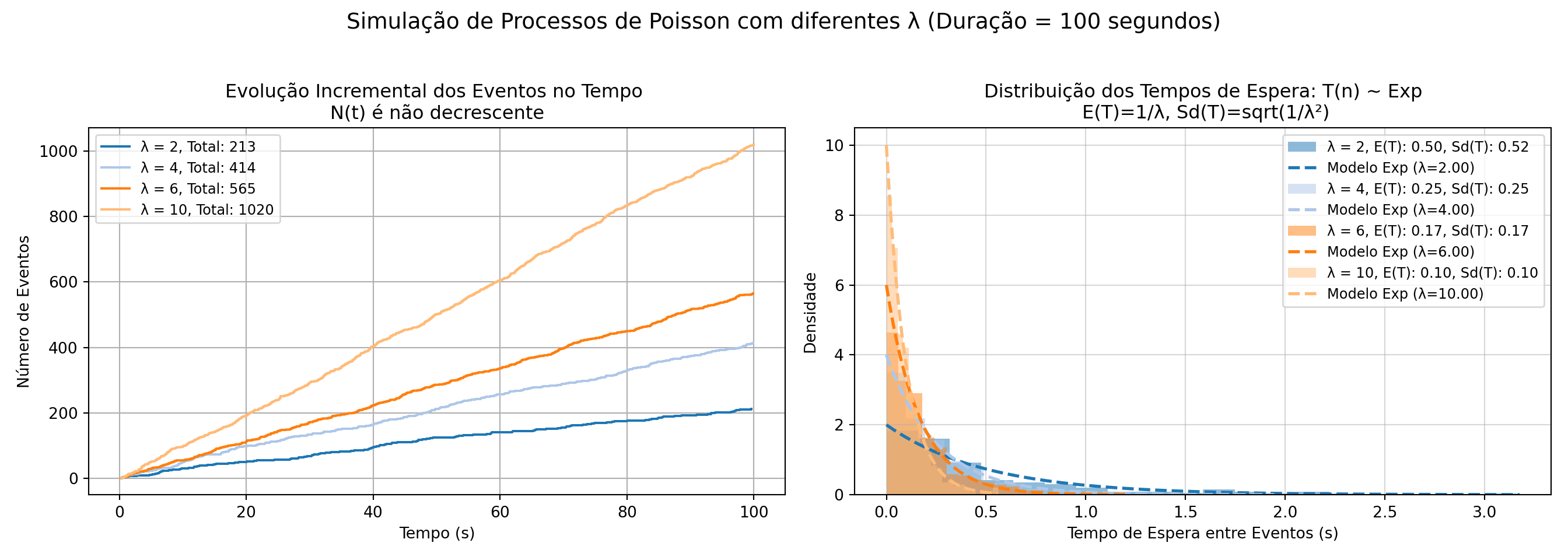
Nas simulações a seguir confirma-se empiricamente que a evolução incremental da contagem de eventos ao longo do tempo (a variável aleatória \(N(t)\)) é crescente e a distribuição dos tempos de espera (a variável aleatória \(T(n)\) entre eventos segue um modelo exponencial com parametro 1/λ (código adaptado de link).
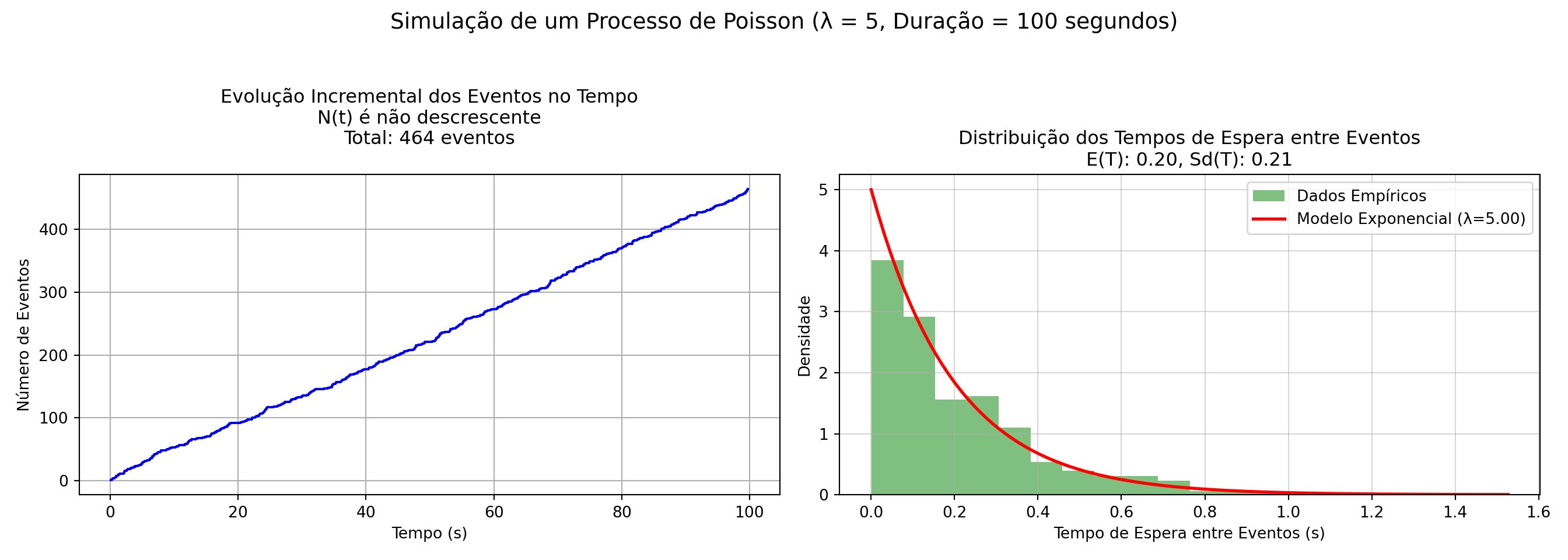
Exemplo 3: Em um sistema de atendimento telefônico, as chamadas chegam de acordo com um processo de Poisson com taxa média de chegada de λ=3 chamadas por minuto. Responda:
1) Qual é a probabilidade de que ocorram exatamente 2 chamadas em um intervalo de 1 minuto?
2) Qual a probabilidade do tempo entre chamadas ser menor que 20 segundos?
3) Sabendo que o sistema comporta sem interrupção o atendimento de até 6 chamadas por minuto, qual é a probabilidade do sistema apresentar falhas?
4) Sabendo que o sistema comporta sem interrupção o atendimento com um intervalo mínimo de 15 segundos entre elas, qual é a probabilidade do sistema apresentar falhas?
- A probabilidade de ocorrerem exatamente \(k = 2\) chamadas em 1 minuto é dada pela fórmula da distribuição de Poisson:
\[ P(N(t) = k) = \frac{(\lambda t)^k e^{-\lambda t}}{k!}\\ P(N(1) = 2) = \frac{(3 \cdot 1)^2 e^{-3}}{2!}\\ P(N(1) = 2) = \frac{9 e^{-3}}{2}\\ P(N(1) = 2) \approx \frac{9 \cdot 0.0498}{2} = 0.2241 \]
- A probabilidade de tempo entre chamadas ser menor que 20 segundos é
\[ P(T \leq t) = 1 - e^{-\lambda t}\\ P(T \leq 1/3) = 1 - e^{-3 \cdot \frac{1}{3}}\\ P(T \leq 1/3) \approx 1 - 0.3679 = 0.6321 \]
- Sabendo que o sistema comporta sem interrupção o atendimento de até 6 chamadas por minuto, a interrupção ocorrerá quando há mais de 6 chamadas no intervalo de 1 minuto, e a probabilidade disso ocorrer é
\[ P(N(1) > 6) = 1 - P(N \leq 6)\\ P(N(1) > 6 ) = 1- \sum_{k=0}^{6} \frac{3^k e^{-3}}{k!}\\ P(N(1) > 6 \approx 1- 0.967\\ P(N(1) > 6) \approx 0.033\\ \]
- Sabendo que o sistema comporta sem interrupção o atendimento com um intervalo mínimo de 15 segundos entre chamadas consecutivas, a interrupção ocorrerá quando o sistema receber cahamadas com um intervalo menor que 15 s e essa probabilidade será
\[ P(T \leq t) = 1 - e^{-\lambda t}\\ P(T \leq 0.25) = 1 - e^{-3 \cdot 0.25}\\ P(T \leq 0.25) = 1 - e^{-0.75}\\ P(T \leq 0.25) \approx 1 - 0.4724 \\ P(T \leq 0.25) \approx 0.5276 \]
Esses resultados ilustram que:
- É improvável que o sistema falhe devido a mais de 6 chamadas em 1 minuto.
- Há uma alta probabilidade de falha devido a intervalos muito curtos entre chamadas consecutivas.
13.4.5 Distribuição condicional dos tempos de chegada
Considere \(N(t), t \geq 0\) com taxa \(\lambda\). Sabendo-se a priori que um evento ocorreu exatamente no intervalo \((0, t]\), qual a distribuição do tempo até a ocorrência desse evento?
Ou seja, desejamos estimar a probabilidade do evento ter ocorrido em intervalo de tempo \(s\) dado que ocorreu um evento no intervalo \(t\), sendo \(s \leq t\)
\[ P(T_1 < s \mid N(t) = 1), \, s \leq t. \]
Pela hipótese de incrementos independentes e estacionários demonstra-se (Sheldon Ross, in Introduction to Probability Models, \(6^{a}\) ed., Cap. 5) que a distribuição é uniforme no intervalo \((0, t]\) e pode-se verificar que
\[ P(T_1 < s \mid N(t) = 1) = \frac{s}{t}, \, s \leq t. \]
Exemplo 4: Em um sistema de atendimento telefônico, as chamadas chegam de acordo com um processo de Poisson com taxa média de chegada de λ=3 chamadas por minuto. Dado que ocorreram 2 chamadas em 1 minuto, qual é a probabilidade de que o tempo de espera para a primeira chamada seja inferior a 20 segundos?
A probabilidade de que o tempo de espera para a primeira chamada seja inferior a \(s=\frac{1}{3} min\) dado que ocorreram 2 chamadas em \(t=1min\) segue uma distribuição uniforme
\[
P(T_1 < s \mid N(t) = 1) = \frac{s}{t}, \, s \leq t.\\
P(T_1 < \frac{1}{3} \mid N(t=1) = 1) = \frac{\frac{1}{3}}{1}\\
P(T_1 < \frac{1}{3} \mid N(t=1) = 1) \approx 0.0333
\]
Dado que ocorreram 2 chamadas em 1 minuto, a probabilidade de que a primeira chamada ocorra nos primeiros 20 segundos é de 1/3 (aproximadamente 33,33%).