11.11 Testes não paramétricos

Um teste não paramétrico (às vezes chamado de teste livre de distribuição) não assume nada sobre a distribuição subjacente (por exemplo, que os dados vêm de uma distribuição Normal ). Isso não equivale a dizer que não se saiba nada sobre a população de origem. Geralmente significa que se sabe que os dados populacionais não são de uma distribuição Normal .

Tipos de testes não paramétricos

Teste de sinal;
Teste de Sinal de Wilcoxon;
Teste de Friedman;
Teste de Mann-Whitney;
Teste de Kruskal Wallis; e,
Teste qui-quadrado.

Há um conjunto importante de testes de hipóteses que possibilita a análise de frequências que ocorrem nas classes de um fator.

Esses testes de hipóteses são muitas vezes referenciados como testes qui-quadrado porque a estatística do teste possui, de modo assintótico, distribuição qui-quadrado.

Embora esses testes se enquadrem em categorias distintas, compartilham algumas características comuns:

Em cada situação considera-se a amostra aleatória, gerada por um ou mais experimentos multinomiais, independentes, de uma ou mais populações multinomiais. Obviamente, a população Bernoulli e a população binomial são casos particulares.
A amostra aleatória é formada pelas frequências observadas nas classes, definidas pela classificação de cada uma das unidades de observação de acordo com um ou mais critérios de interesse. Em todas as situações, a estatística do teste envolve a comparação entre frequências observadas e frequências esperadas, obtidas sob a hipótese de nulidade. Na essência, o teste qui-quadrado verifica hipóteses sobre as probabilidades e utiliza a discrepância existente entre as frequências observadas e as frequências esperadas para concluir sobre elas. Basicamente, dispõe-se de observações (contidas na amostra) sobre uma ou mais populações e busca-se determinar de qual população multinomial essa amostra veio. A hipótese de nulidade especifica a população de interesse.
Se as probabilidades não forem completamente especificadas, algumas probabilidades (e, consequentemente, frequências esperadas) deverão ser estimadas pelos dados, reduzindo os graus de liberdade da distribuição limite.
Como mencionado, a distribuição limite da estatística do teste é a distribuição qui-quadrado. Uma regra usualmente exigida para uma boa aproximação da distribuição qui-quadrado é que a frequência esperada seja maior ou igual a 5. Evidentemente, quanto maiores forem as frequências esperadas, melhor será a aproximação.

Testes paramétricos exigem que a variável seja numérica e várias hipóteses relativas aos parâmetros sejam satisfeitas, tais como que os dados tenham uma distribuição Normal (ou a sigam assintoticamente) ou ainda, em alguns casos que, suas variâncias sejam homogêneas (homocedasticidade) e as amostras tenham um certo tamanho ou frequência observada mínimos.

Testes não paramétricos não assumem nenhum tipo de distribuição e são menos exigentes, podendo também trabalhar com variáveis não numéricas. Como regra geral, opta-se por testes não paramétricos quando:

os valores observados forem extraídos de populações que não possuem uma aproximação com a distribuição Normal;
as populações de origem não possuem homogeneidade de variâncias (heterocedasticidade); e,
as variáveis em estudo não apresentem medidas intervalares que possibilitem o cálculo de estatísticas tais como a média e desvios.

11.11.1 Teste Qui-quadrado para verificação da independência (homogeneidade)

O Teste Qui-quadrado de homogeneidade (ou independência) é um teste estatístico aplicado a dados categóricos para avaliar quão provável é que qualquer diferença observada nas proporções observadas entre os vários níveis de uma variável categórica em populações diferentes (ou níveis de uma segunda variável categórica) seja simples decorrência do acaso; ou seja, o teste Qui-quadrado é geralmente usado verificar quão homogêneas são entre si as frequências observadas não havendo, portanto, diferença estatisticamente significativa entre as populações (ou variáveis).

Diferenças entre o teste Qui-quadrado de homogeneidade e de independência:

Teste Qui-quadrado de homogeneidade: selecionamos uma amostra de elementos de cada uma das populações e distribuímos os elementos de cada uma dessas amostras segundo as categorias da variável estudada; e,
Teste Qui-quadrado de independência: distribuímos uma amostra de n elementos de apenas uma população segundo as categorias da primeira variável categórica A e as da segunda variável categórica B.

Esse tipo de investigação equivale à realização de Teste de Hipóteses onde a hipótese nula que pressupõe que exista homogeneidade (independência) na distribuição das contagens observadas em cada uma das categorias da variável nas populações amostradas (ou níveis da outra variável, no teste Qui-quadrado de Independência) será confrontada com a hipótese alternativa, de que não são homogêneas (dependência) e as flutuações não são podem ser atribuídas ao acaso.

Desse modo o foco será buscar evidência estatística robusta o suficiente que confirmem que as frequências observadas entre as diferentes populações (ou níveis da outra variável, no teste Qui-quadrado de Independência) podem ser consideradas homogêneas (independentes) sob um dado nível de significância $\alpha$.

Consideremos para isso a tabela genérica para a realização do Teste Qui-quadrado onde em cada célula (habitualmente chamada de casela) temos uma frequência (uma quantidade) observada na Tabela a seguir.

Tabela (r × s) de frequências observadas

Variável categórica	B₁	B₂	…	Bs	Total
A₁	n_(1, 1)	n_(1, 2)	…	n_(1, s)	n_(1, .)
A₂	n_(2, 1)	n_(2, 2)	…	n_(2, s)	n_(2, .)
…	…	…	…	…	…
A_r	n_(r, 1)	n_(r, 2)	…	n_(r, s)	n_(r, .)
Totais	n_(., 1)	n_(., 2)	…	n_(., s)	n_(., .)

Notação utilizada na tabela:

$r$ é o número de linhas da tabela;
$s$ é o número de colunas da tabela;
$i$ indexa a i-ésima linha da tabela;
$j$ indexa a j-ésima coluna da tabela;
$n_{i,j}$ indica o elemento localizado na casela situada na i-ésima linha e j-ésima coluna;
$n_{(1,.)}$ indica o último elemento da primeira linha;
$n_{(.,1)}$ indica o último elemento da primeira coluna;e,
$n_{(.,.)}$ indica o último elemento simultaneamente das linhas e colunas da tabela.

Quantas observações devemos ter em cada casela da tabela acima para que as proporções observadas de $A$ e $B$ sejam consideradas estatisticamente homogêneas (independentes)?

Se $A$ e $B$ forem independentes então $P(A_{i} \cap B_{j})= P(A_{i}) \times P(B_{j})$.

O número esperado de observações com as características ($A_{i}$ e $B_{j}$) entre as $n_{.,.}$ observações - sob a hipótese de homogeneidade (independência) da distribuição das contagens observadas entre das variáveis (ou da variável nas populações) - em cada casela deverá ser:

\[\begin{align*} E_{(i,j)} & = n_{(.,.)} \times p_{(i,j)} \\ & = n_{(.,.)} \times p_{(i,.)} \times p_{(.,j)} \\ & = n_{(.,.)} \times \frac{n_{(i,.)}}{n_{(.,.)}} \times \frac{n_{(.,j)}}{n_{(.,.)}}\\ \end{align*}\]

Assim, o valor esperado - sob a hipótese de homogeneidade (independência) da distribuição das contagens observadas entre as variáveis (ou da variável nas populações) $A$ e $B$ - em cada célula deverá ser:

\[ E_{(i,j)} = \frac{n_{(i,.)} \times n_{(.,j)}}{n_{(.,.)}} \]

Em que:

$E_{(i,j)}$ é o valor esperado na casela $(i,j)$;
$n_{(i,.)}$ é o total observado na linha $i$;
$n_{(.,j)}$ é o total observado na coluna $j$; e,
$n_{(.,.)}$ é o total geral observado.

Para a aplicação do teste $\chi{2}$ exige-se que:

preferencialmente as amostras sejam grandes ($n \ge 30$);
no máximo 20% das caselas tenham uma frequência esperada menor que 5; e,
em nenhuma casela a frequência esperada pode ser menor que 1.

A estatística ($X$) do Teste Qui-quadrado de homogeneidade (independência) baseia-se na diferença (dsitância) entre as contagens observados e as contagens esperadas sob a suposição de homogeneidade (independência) pode ser definida da seguinte maneira:

\[ X=\sum_{i=1}^r\sum_{j=1}^s \frac{(O_{(i,j)} - E_{(i,j)})^2}{E_{(i,j)}} \sim \chi^{2}_{((r-1)\times(s-1))} \]

e sua correspondente distribuição:

\[ X\sim \chi^{2}_{((r-1)\times(s-1))} \]

A hipótese nula postula que não há associação: as variáveis são independentes. A flutuação observada nas contagens é devida apenas a fatores puramente aleatórios.

A hipótese alternativa a contradiz, afirmando existir algum fator não aleatório (alguma forma de associação) que resulta na distribuição não homogênea entre as contagens observadas: há dependência entre as variáveis.

\[ \begin{cases} H_{0}: \text{ as variáveis são independentes (a flutuação nas contagens é aleatória}) \\ H_{1}: \text{ as variáveis não são independentes (há alguma associação}) \end{cases} \]

A distribuição de referência que permite julgar se um determinado valor da estatística $X$ pode ser considerado grande o suficiente para rejeitar $H_{0}$ em favor de $H_{1}$ é a chamada distribuição Qui-quadrado: $\chi^{2}$.

Formulação do teste:

teste de hipóteses unilateral à direita (tipo: maior que):

\[\begin{align*} P[X_{calc} \le {\chi^{2}}_{tab \left(\alpha ;(r-1)\times(s-1) \right)} | IND]& =(1-\alpha)\\ P(X_{calc} \le \chi^{2}_{tab \left(\alpha ;(r-1)\times(s-1) \right)})&=(1-\alpha) \end{align*}\]

A região de não rejeição da hipótese nula pode ser vista na Figura 11.30.

prob_desejada=0.95
r=4
s=3
df=(r-1)*(s-1)

q_desejado=round(qchisq(prob_desejada,df), 4)
d_desejada=dchisq(q_desejado,df)



ggplot(data.frame(x = c(0, 30)), aes(x)) +
  stat_function(fun = dchisq,
                geom = "area",
                fill = "lightgrey",
                xlim = c(0,q_desejado),
                colour="black",
                args=list(df=df) )+
  stat_function(fun = dchisq,
                geom = "area",
                fill = "red",
                xlim = c(q_desejado,30),
                colour="black",
                args = list(df = df))+
  scale_y_continuous(name="Densidade") +
  #scale_x_continuous(name="Valores score (f)", breaks = c(f_desejado1, f_desejado2))+  
  scale_x_continuous(name="Valores score (X)")+  
  labs(title="Curva da função densidade \nDistribuição Qui-quadrado", 
  subtitle = "P(0; x crítico)=(1-\u03b1) em cinza (nível de confiança) \nP(x crítico ; \U221e)= \u03b1 em vermelho (nível de significância) ")+
  geom_segment(aes(x = q_desejado, y = 0, xend = q_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=q_desejado+0.5, y=d_desejada, label="x crítico", angle=90, vjust=0, hjust=0, color="blue",size=4)+
 annotate(geom="text", x=q_desejado+5, y=d_desejada, label="Zona de rejeição \n(para x calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=q_desejado-5, y=d_desejada, label="Zona de não rejeição  \n(para x calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()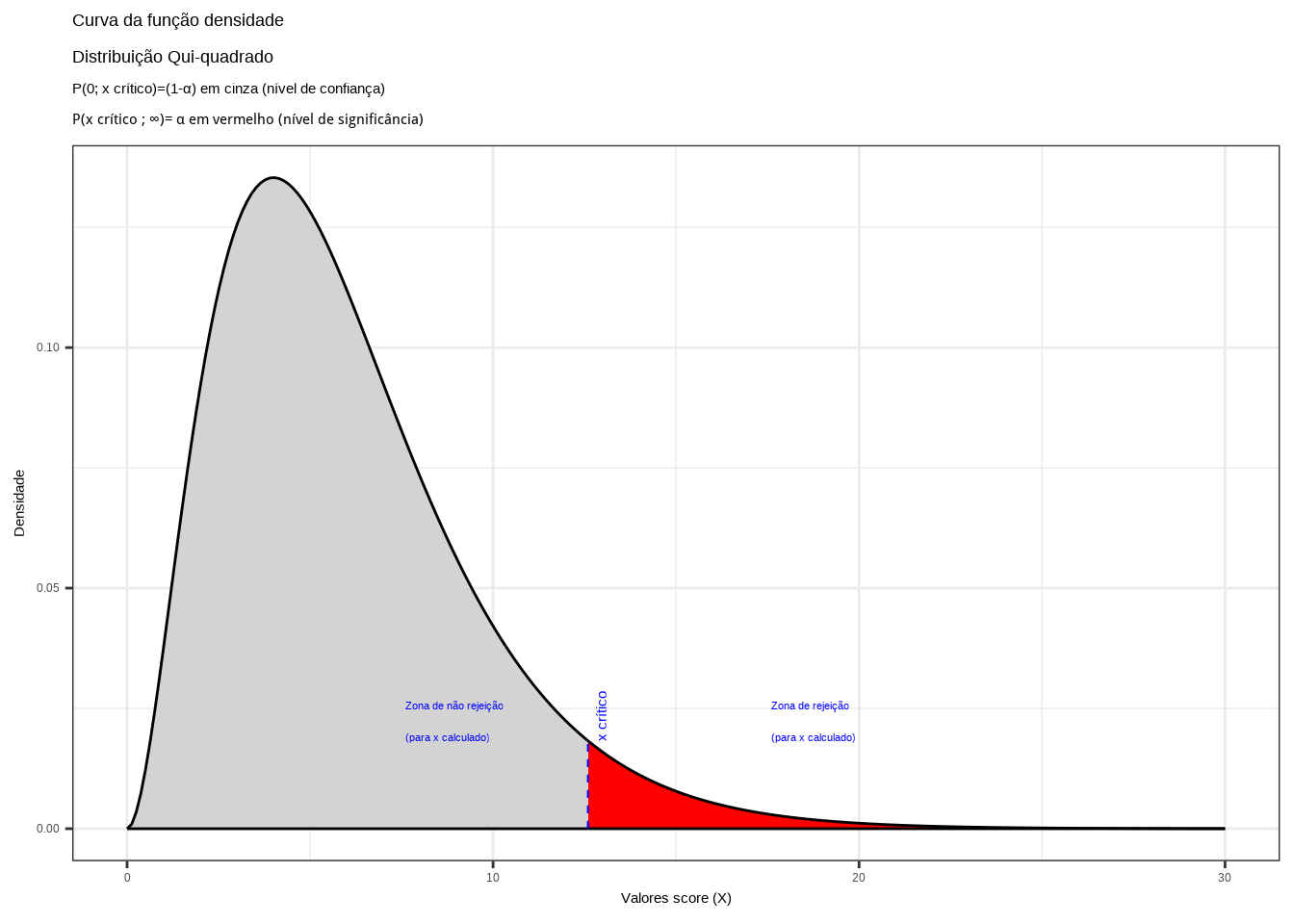

$Região de rejeição da hipótese nula para o teste uniletaral à direita (tipo: menor que): a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $x_{crit}$ para o nível de significância pretendido ($\alpha$ em uma cauda) e ($df$) graus de liberdade.$

Figure 11.30: Região de rejeição da hipótese nula para o teste uniletaral à direita (tipo: menor que): a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $x_{crit}$ para o nível de significância pretendido ($\alpha$ em uma cauda) e ($df$) graus de liberdade.

Exemplo: verifique a independência (homogeneidade) nas contagens da intenção de voto de quatro candidatos distintos em amostras de três diferentes bairros, partindo das informações consolidadas na tabela abaixo.

Pesquisa sobre intenção de votos nos bairros “A”, “B” e “C”
Candidato	Bairros			Total
2-4	“A”	“B”	“C”
Candidato “A”	70	44	86	200
Candidato “B”	50	30	45	125
Candidato “C”	10	6	34	50
Candidato “D”	20	20	85	125
Totais	150	100	250	500

estrutura das hipóteses para o teste a um nível de significância: 0,05

\[ \begin{cases} H_{0}: \text{as contagens são homogêneas} \\ H_{1}: \text{as contagens não são homogêneas} \end{cases} \]

Equivale dizer que há independência entre a escolha de um ou outro candidato e o bairro em questão (não há relação entre um determinado bairro e um determinado candidato)

Estatística do teste e sua distribuição:

\[ X=\sum_{i=1}^r\sum_{j=1}^s \frac{(O_{(i,j)} - E_{(i,j)})^2}{E_{(i,j)}} \sim \chi^{2}_{((r-1)\times(s-1))} \]

Cálculo da frequência esperada em cada casela ($E_{(i,j)}$):

\[ E_{(i,j)} = \frac{n_{(i,.)} \times n_{(.,j)}}{n_{(.,.)}} \]

\[ \frac{\text{soma da linha i} \times \text{soma da coluna j}}{\text{total de observações}} \]

As frequências esperadas em cada casela ($i,j$) serão calculadas pela fórmula acima seguir e estão apresentadas na tabela a segui, em conjunto com as frequências observadas.

Pesquisa sobre intenção de voto nos bairros “A”, “B” e “C”: frequências observadas (e entre parênteses e negrito as frequências esperadas)
Candidato	Bairros			Total
2-4	“A”	“B”	“C”
Candidato “A”	70 (60)	44 (40)	86 (100)	200
Candidato “B”	50 (37,5)	30 (25)	45 (62,5)	125
Candidato “C”	10 (15)	6 (10)	34 (25)	50
Candidato “D”	20 (37,5)	20 (25)	85 (62,5)	125
Totais	150	100	250	500

Nenhuma casela teve frequência esperada menor que 1 nem tampouco observou-se casela com frequência inferior a 5.

Cálculo da estatística do teste:

\[ X=\sum_{i=1}^4\sum_{j=1}^3 \frac{(O_{(i,j)} - E_{(i,j)})^2}{E_{(i,j)}} = 37,88 \]

Da tabela $\chi^{2}$ para o total de graus de liberdade $((r-1)\times(s-1))=(4-1)\times(3-1)=6$ obtemos o valor crítico da estatística do teste ($\chi^{2}_{crit(6)}=12,60$).

prob_desejada=0.95
r=4
s=3
df=(r-1)*(s-1)

q_desejado=round(qchisq(prob_desejada,df), 4)
d_desejada=dchisq(q_desejado,df)


q_calculado=37.88
d_calculado=dchisq(q_calculado,df)


ggplot(data.frame(x = c(0, 50)), aes(x)) +
  stat_function(fun = dchisq,
                geom = "area",
                fill = "lightgrey",
                xlim = c(0,q_desejado),
                colour="black",
                args=list(df=df) )+
  stat_function(fun = dchisq,
                geom = "area",
                fill = "red",
                xlim = c(q_desejado,40),
                colour="black",
                args = list(df = df))+
  scale_y_continuous(name="Densidade") +
  #scale_x_continuous(name="Valores score (f)", breaks = c(f_desejado1, f_desejado2))+  
  scale_x_continuous(name="Valores score (X)")+  
  labs(title="Curva da função densidade \nDistribuição Qui-quadrado", 
  subtitle = "P(0; 12,60)=(1-\u03b1) em cinza (nível de confiança) \nP(12,60 ; \U221e)= \u03b1 em vermelho (nível de significância) ")+
  geom_segment(aes(x = q_desejado, y = 0, xend = q_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=q_desejado+0.5, y=d_desejada, label="x crítico=12,60", angle=90, vjust=0, hjust=0, color="blue",size=4)+
 annotate(geom="text", x=q_desejado+5, y=d_desejada, label="Zona de rejeição \n(para x calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=q_desejado-5, y=d_desejada, label="Zona de não rejeição  \n(para x calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
   geom_segment(aes(x = q_calculado, y = 0, xend = q_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=q_calculado+0.5, y=d_calculado, label="x calculado=37,88", angle=90, vjust=0, hjust=0, color="blue",size=4)+
  theme_bw()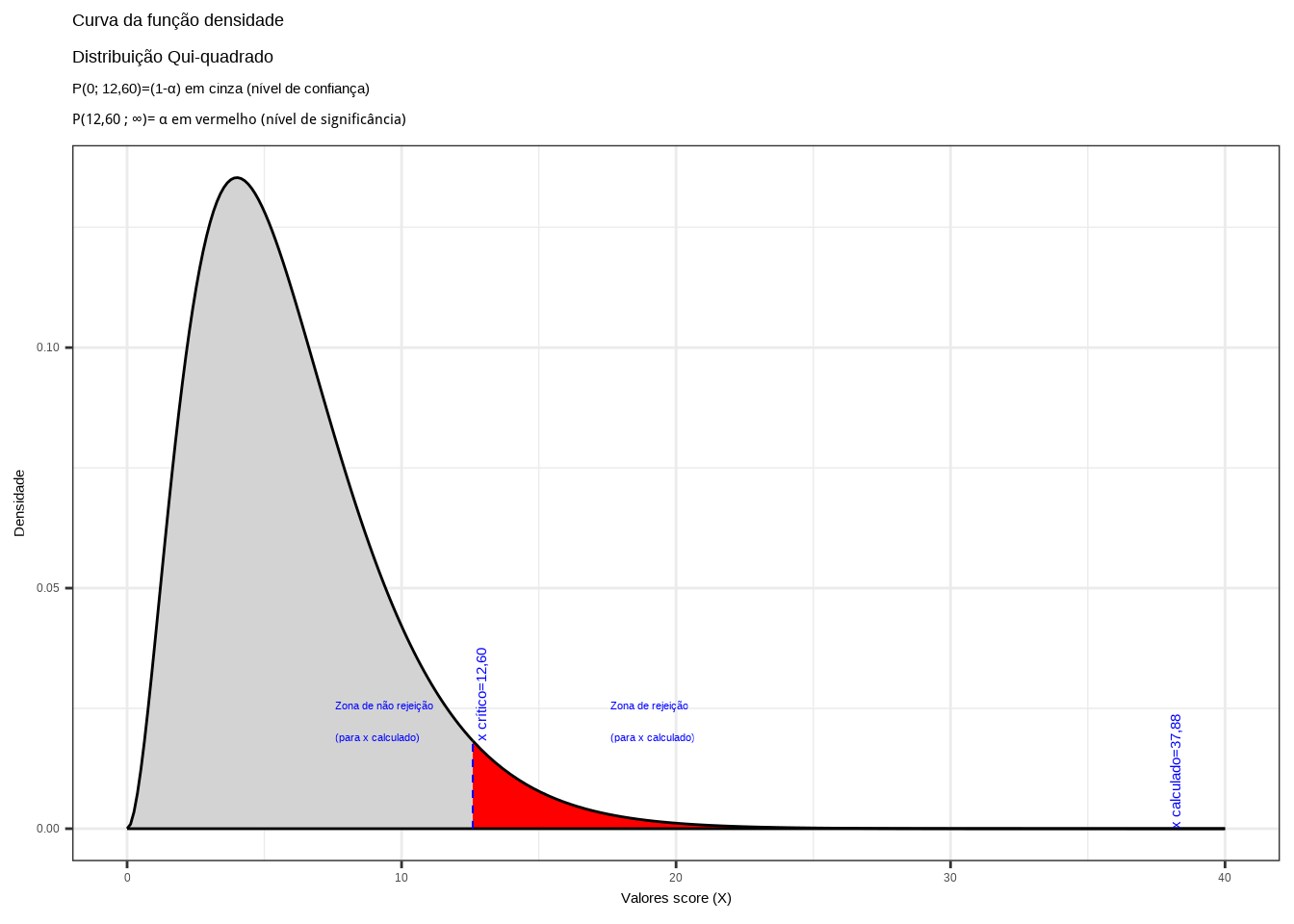

$Região de rejeição da hipótese nula para o teste uniletaral à direita (tipo: menor que): a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $x_{crit}=12,60$ para o nível de significância pretendido ($\alpha=0,05$ em uma cauda) e ($df=6$) graus de liberdade.$

Figure 11.31: Região de rejeição da hipótese nula para o teste uniletaral à direita (tipo: menor que): a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $x_{crit}=12,60$ para o nível de significância pretendido ($\alpha=0,05$ em uma cauda) e ($df=6$) graus de liberdade.

Conclusão: face aos dados trazidos à análise rejeitamos a proposição de que a preferência por um determinado candidato não esteja de algum modo associada ao bairro pesquisado sob um nível de significância de 5% (a probabilidade de cometimento de um erro tipo I. Há alguma relação entre a preferência por um ou outro candidato e os bairros (Figura 11.31). .

11.11.2 Correção de continuidade em tabelas 2x2

Em tabelas de dimensão 2x2, especialmente quando as amostras não forem muito grandes, recomenda-se aplicar a chamada correção de continuidade de Yates, que consiste em reduzir 0,5 unidade nas diferenças absolutas entre as frequências observadas e esperadas:

\[ X=\sum_{i=1}^r\sum_{j=1}^s \frac{(|O_{(i,j)} - E_{(i,j)}|-0,5)^2}{E_{(i,j)}} \]

Ou seja, em cada casela, depois de calculada a diferença entre a frequência observada e a frequência esperada, tomamos o módulo dessa operação (isto é, despreza-se o sinal $\pm$ ) e reduz-se esse valor em 0,5 unidade para, em seguida, elevamos ao quadrado e então dividir-se pela frequência esperada da célula.

11.11.3 Coeficiente de contingência de Pearson (modificado: $C^{*})$ }

Como vimos, a aplicação do teste qui-quadrado permite verificar se existe associação entre duas variáveis, com base em um conjunto de observações. A intensidade dessa associação pode ser quantificada por coeficientes que têm por objetivo medir a força da associação entre duas variáveis categorizadas. Um deles é o chamado coeficiente de contingência de Pearson modificado (uma correção em razão da dimensão da tabela).

Um coeficiente de associação, aplicado a uma tabela de contingência, produz um valor numérico que descreve se os dados se aproximam mais de uma situação de independência ($C^{*}=0$) ou de uma situação de associação ou dependência perfeita ($C^{*}=1$).

\[ C^{*} = \sqrt{ \frac{k \times X^{2}}{(k-1)\times (n + X^{2}) } } \]

em que:

$k$ é o menor valor entre o número de linhas (l) e de colunas (c) da tabela;
$n$ é o número de elementos da tabela; e,
$X{2}$: valor calculado da estatística do teste qui-quadrado.

Exemplo: no exercício resolvido anteriormente ($X^{2}=37,88$ e uma tabela $3 \times 4$ com 500 observaçoes) teremos o seguinte valor para o coeficiente de contingência modificado ($C^{*}$:)

\[\begin{align*} C^{*} & = \sqrt{ \frac{k \times X^{2}}{(k-1)\times (n + X^{2}) } }\\ & = \sqrt{ \frac{3 \times 37,88}{(3-1)\times (500 + 37,88) } }\\ & = \sqrt{ \frac{113,64}{(2)\times (537,88) } }\\ & = \sqrt{0,105637}\\ & = 0,325 \end{align*}\]

11.11.4 Teste Qui-quadrado para verificação da qualidade do ajuste a uma distribuição teórica de probabilidade

O teste de ajuste de qui-quadrado é um teste não paramétrico usado para descobrir como o valor observado de um dado fenômeno é significativamente diferente do valor esperado.

No teste de ajuste do qui-quadrado, o termo qualidade de ajuste ( goodness-of-fit ) é usado para comparar a distribuição da amostra observada com uma distribuição teórica de probabilidade esperada. O teste de ajuste do qui-quadrado determina quão bem a distribuição teórica (como Normal, binomial ou Poisson) se encaixa na distribuição empírica.

No teste de ajuste do qui-quadrado, os dados da amostra são divididos em intervalos. Em seguida, os números de pontos que se enquadram no intervalo são comparados, com o número esperado de pontos em cada intervalo. Considere-se a seguinte tabela com as observações agrupadas em classes.

Dados observados agrupados em classes
ID	Classes	Frequência observada (f_{obs_i})	Frequência teórica esperada (f_{esp_i})	$\frac{(f_{obs_i} - f_{esp_i})^{2}}{f_{esp_i}}$
1	lim_inf ⊢ lim_sup	f_obs₁	f_esp₁	…..
2	lim_inf ⊢ lim_sup	f_obs₂	f_esp₂	…..
…	…	…	….	….
k	lim_inf ⊢ lim_sup	f_{obs_k}	f_{esp_k}
Totais	-	$\sum_{i=1}^{k}f_{obs_i}$	-	$X_{calc}= \sum_{i=1}^{k} \frac{(f_{obs_i} - f_{esp_i})^{2}}{f_{esp_i}}$

A frequência esperada em cada classe, sob a suposição de que os dados seguem uma distribuição Normal: $X \sim \mathcal{N}(\mu, \sigma)$ é dada por:

\[\begin{align*} f_{esp_{i}} & = P[ lim_{inf_{i}} \le X \le lim_{sup_{i}} ]\times \sum_{i=1}^kf_{obs_{i}}\\ & = P[ \frac{(lim_{inf_{i}}-\mu)}{\sigma} \le Z \le \frac{(lim_{sup_{i}}-\mu)}{\sigma} ]\times \sum_{i=1}^kf_{obs_{i}}\\ \end{align*}\]

Há de se considerar duas situações: $\mu$ e $\sigma$ conhecidos, ou estimados a partir dos dados da amostra.

Caso sejam conhecidos, demonstra-se que $X_{calc} \sim \chi^{2}_{(k-1)}$; na outra situação, se forem estimados a partir da amostra (usando-se $\stackrel{-}{x}$ e $s$) então, igualmente, tem-se que $X_{calc} \sim \chi^{2}_{(k-1-2)}$, apenas com a perda de dois graus de liberdade pelas estimações feitas.

A estatística do teste qui-quadrado de qualidade de ajuste baseia-se na distância entre as frequências observadas e as frequências esperados sob a distribuição de probabilidade considerada e pode então ser definida, bem como o teste de hipóteses, da seguinte maneira:

\[ X_{calc}= \sum_{i=1}^k \frac{(f_{obs_i} - f_{esp_i})^2}{f_{esp_i}} \]

Demonstra-se que para uma amostra grande e com classes com frequências esperadas ($f_{esp_i}\ge 5$) que $X_{calc} \sim \chi^{2} (k-1)$ e o correspondente teste de hipóteses assume a estrutura seguinte:

\[ \begin{cases} H_{0}: \text{X segue o modelo teórico proposto} \\ H_{1}: \text{X não segue o modelo proposto} \end{cases} \]

Formulação do teste:

Teste de hipóteses unilateral à direita (tipo: maior que):

\[\begin{align*} P[X_{calc} \le {\chi^{2}}_{tab \left(\alpha ;(k-1) \right)} | X \sim \mathcal{N}] & =(1-\alpha) \\ P(X_{calc} \le \chi^{2}_{tab \left(\alpha ;(k-1) \right)}) & =(1-\alpha) \end{align*}\]

prob_desejada=0.95
r=4
s=3
df=(r-1)*(s-1)

q_desejado=round(qchisq(prob_desejada,df), 4)
d_desejada=dchisq(q_desejado,df)



ggplot(data.frame(x = c(0, 30)), aes(x)) +
  stat_function(fun = dchisq,
                geom = "area",
                fill = "lightgrey",
                xlim = c(0,q_desejado),
                colour="black",
                args=list(df=df) )+
  stat_function(fun = dchisq,
                geom = "area",
                fill = "red",
                xlim = c(q_desejado,30),
                colour="black",
                args = list(df = df))+
  scale_y_continuous(name="Densidade") +
  #scale_x_continuous(name="Valores score (f)", breaks = c(f_desejado1, f_desejado2))+  
  scale_x_continuous(name="Valores score (X)")+  
  labs(title="Curva da função densidade \nDistribuição Qui-quadrado", 
  subtitle = "P(0; x crítico)=(1-\u03b1) em cinza (nível de confiança) \nP(x crítico ; \U221e)= \u03b1 em vermelho (nível de significância) ")+
  geom_segment(aes(x = q_desejado, y = 0, xend = q_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=q_desejado+0.5, y=d_desejada, label="x crítico", angle=90, vjust=0, hjust=0, color="blue",size=4)+
 annotate(geom="text", x=q_desejado+5, y=d_desejada, label="Zona de rejeição \n(para x calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=q_desejado-8, y=d_desejada, label="Zona de não rejeição  \n(para x calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()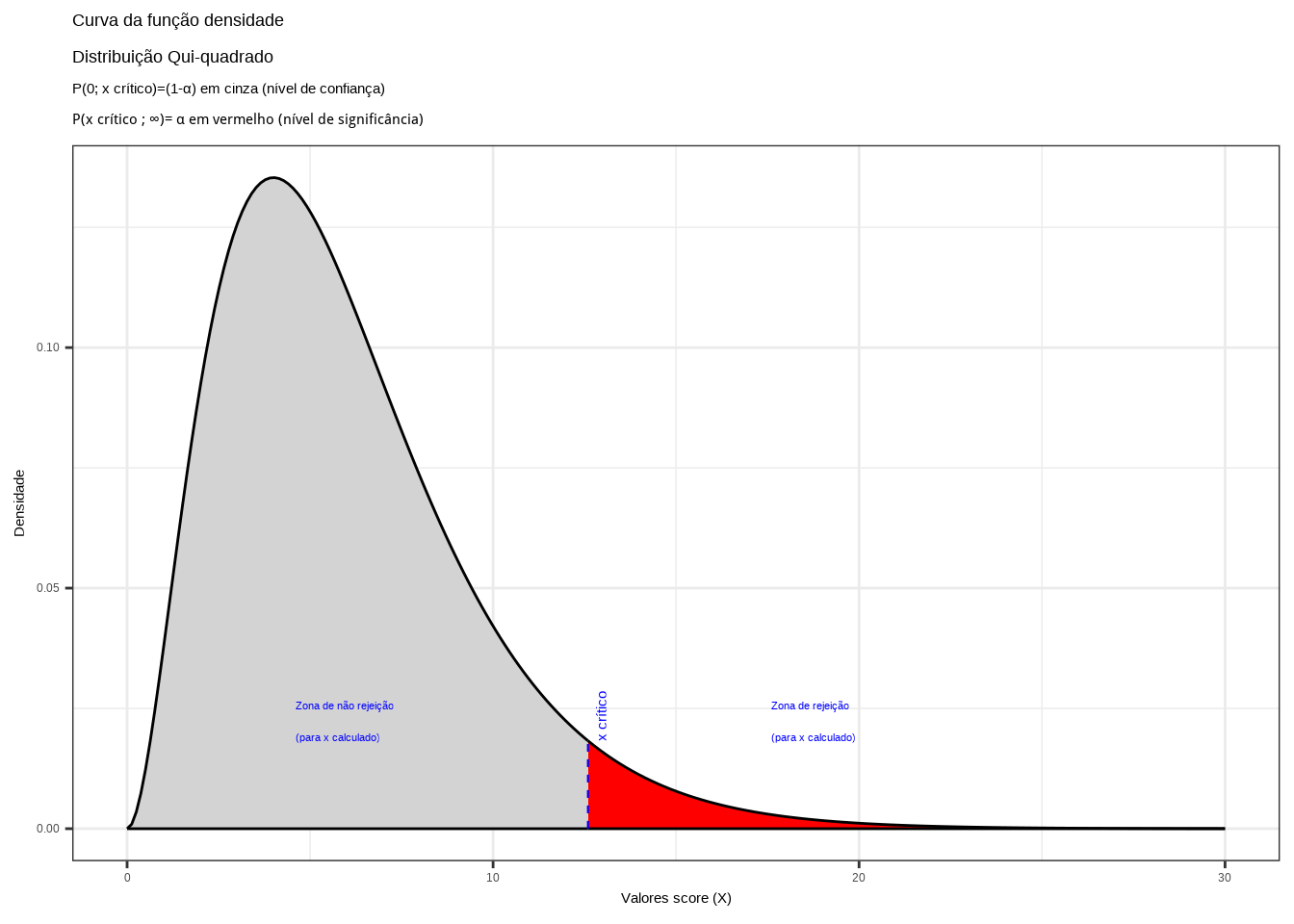

Figure 11.32: Região de rejeição da hipótese nula para o teste uniletaral à direita (tipo: menor que): a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $x_{crit}$ para o nível de significância pretendido ($\alpha$ em uma cauda) e ($df$) graus de liberdade.

Exemplo: deseja-se verificar a afirmação de que a porcentagem de cinzas (material estranh ao produtoo) contidas em café torrado e moído produzido por certa empresa de torrefação segue uma distribuição Normal. Os dados abaixo representam a quantidade percentual desse material encontradas em 250 amostras analisadas em laboratório. Faça um teste qui-quadrado de adequação das frequências observadas a essa distribuição com um nível de significância $\alpha=0.04$.

Análise da presença de cinzas em café torrado e moído
ID	Cinzas de material	Frequência observada
(k)	estranho (%)	(f_{obs_i})
1	9, 50 ⊢ 10, 50	2
2	10, 50 ⊢ 11, 50	5
3	11, 50 ⊢ 12, 50	16
4	12, 50 ⊢ 13, 50	42
5	13, 50dash14, 50	69
6	14, 50 ⊢ 15, 50	51
7	15, 50 ⊢ 16, 50	32
8	16, 50 ⊢ 17, 50	23
9	17, 50 ⊢ 18, 50	9
10	18, 50 ⊢ 19, 50	1
Totais		250

Análise do problema: verificar se as frequências observadas nas classes diferem das que seriam esperadas se a distribuição dessa variável seguisse uma distribuição Normal com parâmetros $\mu$ e $\sigma$ (não informados pelo enunciado do problema).

Essa omissão nos força a utilizar a média e o desvio padrão amostrais ($\stackrel{-}{x}$ e $S$) como suas estimativas.

Isso irá nos impor a perda adicional de mais dois graus de liberdade na estatística do teste: $\chi^{2}_{(k-1-2)}$.

Para dados agrupados em classes a média e a variância são calculados por:

\[ \sum_{i=1}^k \frac{\stackrel{-}{x_{i}} \cdot f_{obs_{i}}}{n} = 14,512 \]

\[ S^{2} = \frac{\sum_{i=1}^k (\stackrel{-}{x_{i}} -\stackrel{-}{x})^{2} \times f_{obs_{i}}}{n-1} = 2,701 \]

Na sequência, calculam-se as frequências esperadas para cada classe sob a premissa de Normalidade. Abaixo mostramos o cálculo para a primeira classe:

\[\begin{align*} f_{esp_{i}} & = P[ lim_{inf_{i}} \le X \le lim_{sup_{i}} ].\sum_{i=1}^{k}f_{obs_{i}} \\ & = P[ 9,50 \le X \le 10,50 ] \times 250\\ & = P[ \frac{(lim_{inf_{i}}-\mu)}{\sigma} \le Z \le \frac{(lim_{sup_{i}}-\mu)}{\sigma} ] \times \sum_{i=1}^kf_{obs_{i}}\\ & = P[ \frac{(9,50-14,512)}{\sqrt{2,701}} \le Z \le \frac{(10,50-14,512)}{\sqrt{2,701}} ]\times 250\\ & = P[ \frac{(9,50-14,512)}{\sqrt{2,701}} \le Z \le \frac{(10,50-14,512)}{\sqrt{2,701}} ]\times 250\\ & = P[-3,0496 \le Z \le -2,4412 ]\times 250\\ & = (0,4989-0,4927) \times 250\\ & = (0,0062) \times 250\\ & = 1,55\\ \end{align*}\]

Análise da presença de cinzas em café torrado e moído
ID	Cinzas de material	Frequência	Frequência	$\frac{(f_{obs_{i}} - f_{esp_i})^2}{f_{esp_i}}$
(k)	estranho (%)	observada (f_{obs_i})	teórica esperada (f_{esp_i})
1	9, 50 ⊢ 10, 50	2	1,543559
2	10, 50 ⊢ 11, 50	5	6,525845
3	11, 50 ⊢ 12, 50	16	19,25203
4	12, 50 ⊢ 13, 50	42	39,648
5	13, 50 ⊢ 14, 50	69	57,01595
6	14, 50 ⊢ 15, 50	51	57,26207
7	15, 50 ⊢ 16, 50	32	40,16374
8	16, 50 ⊢ 17, 50	23	19,67134
9	17, 50 ⊢ 18, 50	9	6,725776
10	18, 50 ⊢ 19, 50	1	1,604656
Totais		250	-

As frequências esperadas para as classes 1 e 10 são menores que 5 ($f_{esp_i}\ge 5$) impondo que essas duas classes sejam agrupadas às classes imediatamente adjacentes.

Análise da presença de cinzas em café torrado e moído
ID	Cinzas de material	Frequência	Frequência	$\frac{(f_{obs_{i}} - f_{esp_i})^2}{f_{esp_i}}$
(k)	estranho (%)	observada (f_{obs_i})	teórica esperada (f_{esp_i})
1-2	9, 50 ⊢ 11, 50	7	8,069404	0,141724
3	11, 50 ⊢ 12, 50	16	19,25203	0,549329
4	12, 50 ⊢ 13, 50	42	39,648	0,139525
5	13, 50 ⊢ 14, 50	69	57,01595	2,518900
6	14, 50 ⊢ 15, 50	51	57,26207	0,684808
7	15, 50 ⊢ 16, 50	32	40,16374	1,659374
8	16, 50 ⊢ 17, 50	23	19,67134	0,563255
9-10	17, 50 ⊢ 19, 50	10	8,330432	0,334611
Totais		250	-	6,591525

Estrutura do teste: teste de hipóteses unilateral à direita (tipo: maior que):

\[ \begin{cases} H_{0}: X \sim \mathcal{N} (\stackrel{-}{x}, S) \\ H_{1}: \text{X não segue o modelo proposto} \end{cases} \]

A hipótese nula postula que a variável X segue a distribuição Normal ($X \sim \mathcal{N}(\stackrel{-}{x}, S)$)

Estatística do teste:

\[ x_{calc}= \sum_{i=1}^k \frac{(f_{obs_{i}} - f_{esp_i})^2}{f_{esp_i}}=6,59 \]

Valor crítico da estatística de teste $\chi^{2}_{(\alpha), (k-1-2)}$:

\[ \chi^{2}_{(0,04), (8-1-2)}=11,64 \]

prob_desejada=0.96
df=5

q_desejado=round(qchisq(prob_desejada,df), 4)
d_desejada=dchisq(q_desejado,df)


q_calculado=round(6.59, 4)
d_calculada=dchisq(q_calculado,df)


ggplot(data.frame(x = c(0, 30)), aes(x)) +
  stat_function(fun = dchisq,
                geom = "area",
                fill = "lightgrey",
                xlim = c(0,q_desejado),
                colour="black",
                args=list(df=df) )+
  stat_function(fun = dchisq,
                geom = "area",
                fill = "red",
                xlim = c(q_desejado,30),
                colour="black",
                args = list(df = df))+
  scale_y_continuous(name="Densidade") +
  #scale_x_continuous(name="Valores score (f)", breaks = c(f_desejado1, f_desejado2))+  
  scale_x_continuous(name="Valores score (X)")+  
  labs(title="Curva da função densidade \nDistribuição Qui-quadrado", 
  subtitle = "P(0; 11,64)=0,96 em cinza (nível de confiança) \nP(11,64 ; \U221e)= 0,04 em vermelho (nível de significância) ")+
  geom_segment(aes(x = q_desejado, y = 0, xend = q_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=q_desejado+0.5, y=d_desejada, label="x crítico=11,64", angle=90, vjust=0, hjust=0, color="blue",size=4)+
 annotate(geom="text", x=q_desejado+5, y=d_desejada, label="Zona de rejeição \n(para x calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=q_desejado-8, y=d_desejada, label="Zona de não rejeição  \n(para x calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
   geom_segment(aes(x = q_calculado, y = 0, xend = q_calculado, yend = d_calculada), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=q_calculado+0.5, y=d_calculada, label="x calculado=6,59", angle=90, vjust=0, hjust=0, color="blue",size=4)+
  theme_bw()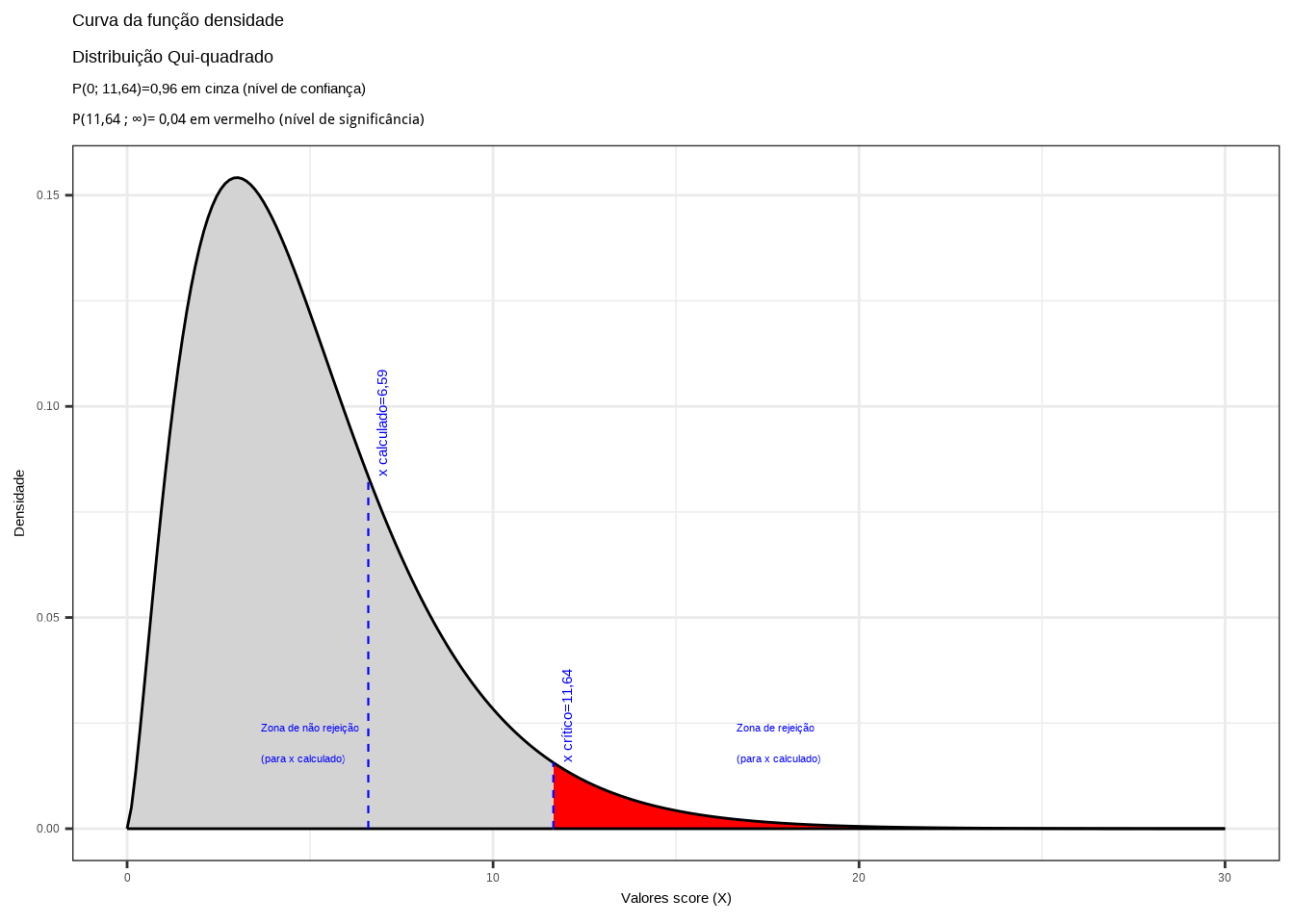

$Região de rejeição da hipótese nula para o teste uniletaral à direita (tipo: menor que): a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $x_{crit}=11,64$ para o nível de significância pretendido ($\alpha$ em uma cauda) e ($df$) graus de liberdade.$

Figure 11.33: Região de rejeição da hipótese nula para o teste uniletaral à direita (tipo: menor que): a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $x_{crit}=11,64$ para o nível de significância pretendido ($\alpha$ em uma cauda) e ($df$) graus de liberdade.

Conclusão:

O resultado do teste de hipóteses realizado com as amostras trazidas à análise não nos permite rejeitar a afirmação de que os seus valores procedem de uma distribuição Normal ($X \sim \mathcal{N}(\stackrel{-}{x}=14,512, S=1,6435)$) a um nível de significância de 4% (Figura 11.33).

11.11.5 Teste de significância para as médias de duas populações dependentes

O Teste ``t’’ emparelhado é usado quando dados das duas amostras são colhidas de um mesmo indivíduo (ensaio clínico) ou em uma mesma unidade experimental (experimento agronômico) havendo, portanto, dependência entre os valores observados.

As possívies estruturas dos testes de hipóteses para duas médias dependentes (amostras emparelhadas) são:

Teste de hipóteses bilateral (tipo: diferente de):

\[ \begin{cases} H_{0}: \mu_{\text{dif}} = \Delta_{0} \\ H_{1}: \mu_{\text{dif}} \ne \Delta_{0} \end{cases} \]

Teste de hipóteses unilateral à esquerda (tipo: menor que):

\[ \begin{cases} H_{0}: \mu_{\text{dif}} \ge \Delta_{0} \\ H_{1}: \mu_{\text{dif}} < \Delta_{0} \end{cases} \]

Teste de hipóteses unilateral à direita (tipo: maior que):

\[ \begin{cases} H_{0}: \mu_{\text{dif}} \le \Delta_{0} \\ H_{1}: \mu_{\text{dif}} > \Delta_{0} \end{cases} \]

em que:

$\Delta_{0}$ é, usualmente, 0 (as médias são iguais); e,
$\mu_{\text{dif}} = \mu_{1} - \mu_{2}$ é a diferença entre os pares de observaçõe.;

Estatística do teste para amostras Normais ($n_{1}$ e $n_{2}$ quaisquer) ou amostras de outras distribuições, mas desde que $n_{1}$ e $n_{2}$ $ $:

$t_{cal} = \frac{\sqrt{n}\cdot \left({\stackrel{-}{x}}_{dif}-{\Delta }_{0}\right)}{{S}_{dif}}$
$\stackrel{-}{x}_{dif}$: valor médio das diferenças entre as observações (amostra)
$S_{dif}$: desvio padrão das diferenças entre as observações (amostra)
${t}_{tab\left(\frac{\alpha }{2}; n-1 \right)}$ ou ${t}_{tab\left(\alpha ; n-1\right)}$: o quantil associado na distribuição ``t’’ de Student ao nível de significância pretendido no teste, com $(n-1)$ graus de liberdade.

Formulação dos testes com a estatística T ($T \sim t_{(n-1)}$):

Teste de hipóteses bilateral (tipo: diferente de):

\[\begin{align*} P[\left|t_{calc}\right| \ge {t}_{tab\left(\frac{\alpha }{2}; n-1 \right)}|\mu_{\text{dif}}=0] & =(1-\alpha)\\ P ( - {t}_{tab\left(\frac{\alpha }{2}; n-1 \right)} \le t_{calc} \le {t}_{tab\left(\frac{\alpha }{2}; n-1 \right)}) & = (1-\alpha)\\ \end{align*}\]

As regiões de rejeição (regiões críticas) da hipótese nula podem ser vistas na Figura 11.14.

Teste de hipóteses unilateral à esquerda (tipo: menor que):

\[\begin{align*} P[t_{calc} \ge {t}_{tab\left(\alpha ; n-1\right)} |\mu_{\text{dif}}=0] & =(1-\alpha)\\ P(t_{calc} \ge {t}_{tab\left(\alpha ; n-1\right)}) & = (1-\alpha) \\ \end{align*}\]

A região de rejeição (região crítica) da hipótese nula pode ser vista na Figura 11.15.

Teste de hipóteses unilateral à direita (tipo: maior que):

\[\begin{align*} P[t_{calc} \le {t}_{tab\left(\alpha ; n-1\right)}|\mu_{\text{dif}}=0] & = (1-\alpha)\\ P( t_{calc} \le {t}_{tab\left(\alpha ; n-1\right)}) & = (1-\alpha)\\ \end{align*}\]

A região de rejeição (região crítica) da hipótese nula pode ser vista na Figura 11.16.

Exemplo: Uma empresa precisa tomar a decisão de adquirir uma nova máquinas de usinagem. Contudo, o fornecedor apresentou dois modelos (A e B) de preços diferentes. Para tomar a decisão, convocou 5 de seus funcionários mais experientes e os despachou para a fábrica, que os treinou a executar a mesma tarefa em ambas as máquinas. A tabela abaixo apresenta os tempos gastos pelos funcionários em ambas as máquinas (cf. tabela $\ref{tab7}$). No nível de significância de 10% podemos afirmar que a tarefa realizada na máquina $A$ demora mais que na máquina $B$?

Tempo necessário para usinagem de uma mesma peça em duas máquinas diferentes, por 5 operadores diferentes
Funcionário	Máquina A (h)	Máquina B (h)
A	80	75
B	72	70
C	65	60
D	78	72
E	85	78

O enunciado do problema deixa bastante claro que as medidas, os tempos gastos para a realização da tarefa nas máquinas A e B foram tomados no mesmo grupo de funcionários, de tal sorte que não nos é possível afirmar que há independência. O Teste ``t’’ é usado quando dados das duas amostras são colhidas de um mesmo sujeito, havendo, portanto dependência entre as amostras. A tabela a seguir apresenta as diferenças de tempo de usinagem entre as máquinas, para cada operador.

Diferenças nos tempos de usinagem
Funcionário	Diferença: A-B (h)
A	5
B	2
C	5
D	6
E	7
Média	5,00
Desvio padrão	1,8708

Estrutura do teste: teste de hipóteses unilateral à direita (tipo: maior que):

\[ \begin{cases} H_{0}: \mu_{\text{dif}} (\mu_{A} - \mu_{B}) \le 0 \\ H_{1}: \mu_{\text{dif}} (\mu_{A} - \mu_{B}) > 0 \end{cases} \]

A hipótese nula afirma que o tempo médio $\mu_{A}$ é igual ou menor que o tempo médio $\mu_{B}$; já a hipótese alternativa, contrariamente, afirma que o tempo médio $\mu_{A}$ é maior que o tempo médio $\mu_{B}$. Estatística do teste:

\[ t_{cal} = \frac{\sqrt{n} \times \left({\stackrel{-}{x}}_{dif}\right)}{{S}_{dif}} \]

\[ t_{calc} > {t}_{tab\left(\alpha ; (n-1)\right)} \]

em que:

$n=5$;
${t}_{tab\left(0,10 ; (5-1) \right)} = 1,533$ é o quantil associado na distribuição ``t’’ de Student no nível de significância pretendido no teste e com $(n-1)$ graus de liberdade (valor crítico monocaudal);
$t_{cal} = \frac{\sqrt{n}\cdot \left({\stackrel{-}{x}}_{dif}\right)}{{S}_{dif}} = 5,97$;
$\stackrel{-}{x}_{dif} = 5,00$ é o valor médio das diferenças entre as observações amostrais;
$S_{dif} = 1,87$: desvio padrão das diferenças entre as observações amostrais.

alfa=0.90
prob_desejada=alfa
df=4
t_desejado=round(qt(prob_desejada,df ),4)
d_desejada=dt(t_desejado,df)

t_calculado=5.97
d_calculado=dt(t_calculado,df)


ggplot(NULL, aes(c(-7,7))) +
  geom_area(stat = "function", 
            fun = dt,
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(-7, t_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "red", 
            xlim = c(t_desejado,7),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de t", breaks = c(t_desejado))  +
  labs(title= 
         "Regiões críticas sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P(-\U221e; 1,53)=(1-\u03b1) em cinza (nível de confiança=0,90) \nP(1,53; \U221e)= \u03b1 em vermelho (nível de significância=0,10) ")+ 
  geom_segment(aes(x = t_desejado, y = 0, xend = t_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
   annotate(geom="text", x=t_desejado-0.1, y=d_desejada, label="Valor crítico da estatística do teste=1,53", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado-3, y=0.1, label="Região de não rejeição da hipótese nula \nprobabilidade=\u03b1", angle=0, vjust=0, hjust=0, color="blue",size=3)+
 annotate(geom="text", x=t_desejado+1, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
 geom_segment(aes(x = t_calculado, y = 0, xend = t_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
 annotate(geom="text", x=t_calculado-0.1, y=d_calculado, label="Valor da estatística do teste=5,97", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()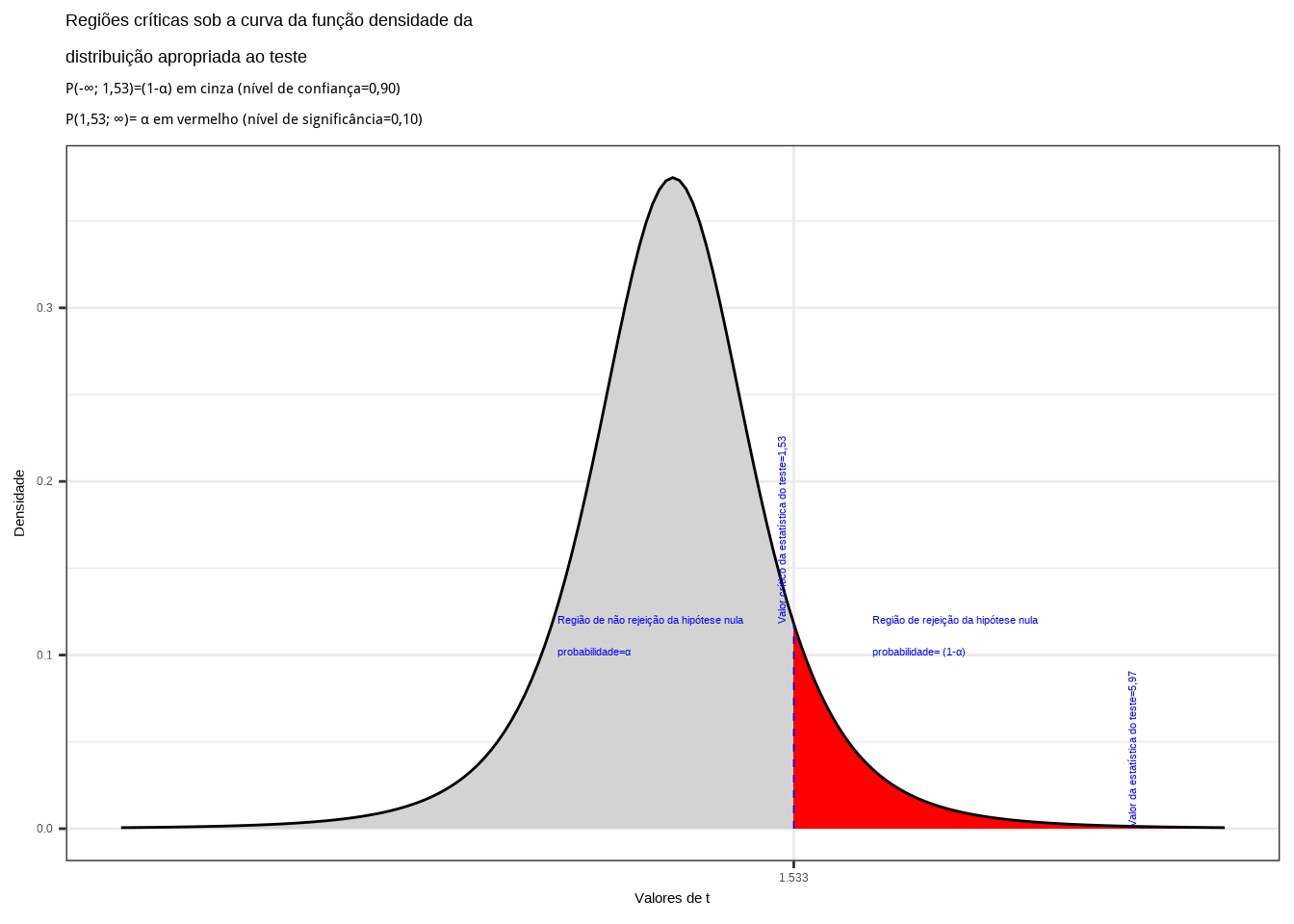

$Região de rejeição da hipótese nula para o teste unilateral à direita (tipo: maior que) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $t_{crit} = 1,53$. O valor calculado da estatística ($t_{calc}=5,97$) situa-se na faixa de significância do teste, não possibilitando a rejeição da hipótese nula sob aquele nível de confiança$

Figure 11.34: Região de rejeição da hipótese nula para o teste unilateral à direita (tipo: maior que) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $t_{crit} = 1,53$. O valor calculado da estatística ($t_{calc}=5,97$) situa-se na faixa de significância do teste, não possibilitando a rejeição da hipótese nula sob aquele nível de confiança

Conclusão:

O resultado do teste de hipóteses realizado com as amostras trazidas à análise não nos permite suportar a afirmação de que o tempo médio para a realização da tarefa na máquina $A$ seja menor ou igual ao tempo médio gasto na máquina $B$ a um nível de significância de 10%. O tempo médio na máquina $A$ é maior (Figura 11.34).

UNIVERSIDADE ESTADUAL DE LONDRINA
CCE - Centro de Ciências Exatas
DSTA - Departamento de Estatística (sala 11)
Prof. M.e Eng.\(^{o}\) Felinto Junior Da Costa
fjcosta@uel.br