8.9 Correlação linear de Pearson

Em estatística, a expressão correlação se refere à relação existente entre variáveis, digamos \(X\) e \(Y\).

Essa relação pode assumir diferentes relações funcionais que, bsicamente podem ser:

linear: positiva ou negativa
não linear: logarítmica, cíclica (periódica), quadrática, cúbica .

A correlação existente entre valores observados de uma mesma variável, digamos \(X\) em diferentes momentos de tempo \(X_{(t_i-1)}, X_{(t_i)}\) é denominada autocorrelação.

É preciso sempre ter em mente que uma correlação estatística, por si só, não implica logicamente em causação. Para atribuir uma relação de causa-efeito deve-se lançar mão de considerações a priori ou teóricas acerca do objeto do estudo.

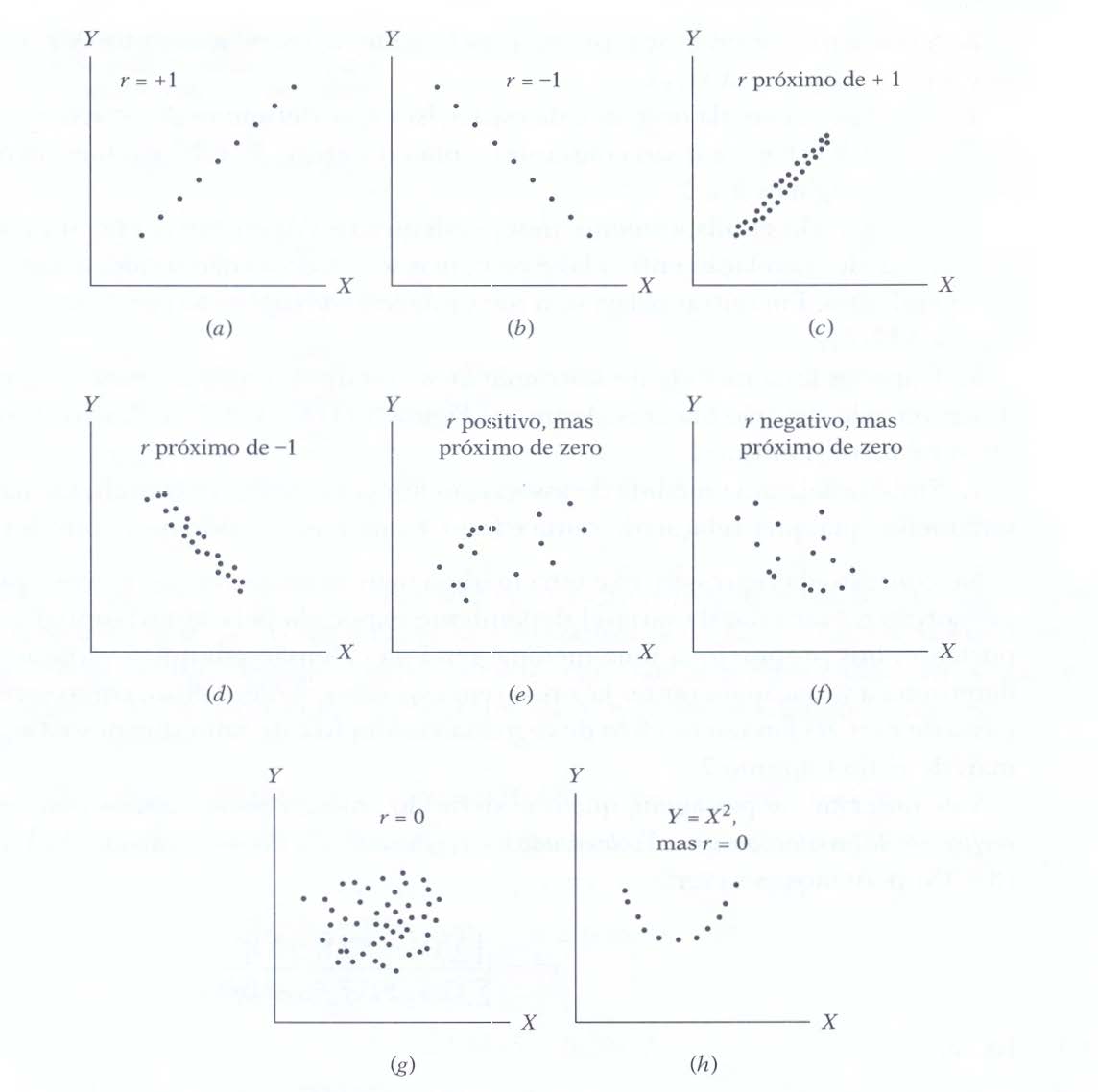
Figure 8.6: Diferentes diagramas de dispersão entre duas variáveis X e Y (Fonte: Introduction to Econometrics. Englewoods Cliffs, 1978)

Em (A), (B), (C) e (D) parece-nos que a relação observada entre as variáveis \(X\) e \(Y\) pode ser expressa por uma função linear (uma reta):

em (A) e (C) vemos que a variação de ocorre no mesmo sentido: quando o valor da variável \(X\) sofre um incremento, também assim ocorre, em algum grau, na variável \(Y\);
em (B) e (D) vemos que uma variação inversa: quando o valor da variável \(X\) sofre um incremento, a variável \(Y\) sofre um decremento em algum grau;
em (A) e (B) parece-nos que uma função linear exprimiria uma relação entre as variáveis \(X\) e \(Y\) de modo exato quando comparada a (C) e (D).

Em (G) não se vislumbra um padrão linear no comportamento das variáveis \(X\) e \(Y\) e em (H) o padrão de comportamento observado entre as variáveis \(X\) e \(Y\) sugere haver uma boa relação, todavia não linear.

O cálculo do Coeficiente de correlação linear de Pearson (r) envolve diversos somatórios dos valores das variáveis \(X\), \(Y\), seus quadrados e também de seu produto \(X.Y\).

\[ r=\frac{\sum _{i=1}^{n}{x}_{i} \cdot {y}_{i} - \frac{\sum _{i=1}^{n}{x}_{i}\sum _{i=1}^{n}{y}_{i}}{n}}{\sqrt{\left(\sum _{i=1}^{n}{x}_{i}^{2}-\frac{{\left(\sum _{i=1}^{n}{x}_{i}\right)}^{2}}{n}\right)\cdot \left[\sum_{i=1}^{n}{y}_{i}^{2}-\frac{{\left(\sum _{i=1}^{n}{y}_{i}\right)}^{2}}{n}\right]}} \]

Na expressão acima:

\(x_{i}\): é o i-ésimo valor observado de \(X\);
\(y_{i}\): é o i-ésimo valor observado de \(Y\); e,
\(n\) é o número de pares de valores observados.

Outra apresentação de sua fórmula de estimação é:

\[ r=\frac{\sum _{i=1}^{n}(x_{i}-\bar{x})\cdot(y_{i}-\bar{y})}{ \sqrt{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2} \cdot \sum_{i=1}^{n}(y_{i}-\bar{y})^{2}} } \]

Na expressão acima:

\(x_{i}\): é o i-ésimo valor observado de \(X\);
\(y_{i}\): é o i-ésimo valor observado de \(Y\);
\(\bar{x}\): é o valor médio das observações \(x\); e,
\(\bar{y}\): é o valor médio das obsrevações \(y\).

Simplificadamente podemos também exprimir \(r\) na forma abaixo:

\[ r=\frac{{S}_{xy}}{\sqrt{{S}_{xx}\cdot {S}_{yy}}} \]

em que:

\[\begin{align*} S_{xy} = & \sum_{i=1}^{n} x_{i}y_{i} - \frac{\sum_{i=1}^{n}x_{i}\cdot\sum_{i=1}^{n}y_{i}}{n} \\ S_{xx} = & \sum_{i=1}^{n} x_{i}^{2} - \frac{(\sum_{i=1}^{n} x_{i})^{2}}{n} \\ S_{yy} = & \sum_{i=1}^{n}y_{i}^{2} - \frac{(\sum_{i=1}^{n} y_{i})^{2}}{n} \end{align*}\]

O coeficiente de correlação de Pearson quantifica a intensidade das relações lineares entre \(x\) e \(y\) e não estabelece per si nenhuma relação de causação.

É apenas uma medida da associação linear entre duas variáveis e, portanto, não tem sentido usá-lo na quantificação de relações que não o sejam.

O coeficiente de correlação linear de Pearson tem uma faixa limitada de variação e é simétrico; isto é, a correlação linear observada entre \(X\) e \(Y\) é a mesma que a medida entre \(Y\) e \(X\).

\[ -1\le r \le 1 \]

se \(r>0\) dizemos que há uma relação linear positiva entre as variáveis estudadas: para um incremento na primeira variável observa-se também um incremento na segunda;
se \(r<0\) a relação linear é negativa: um incremento em uma das variáveis é acompanhado por um decremento na outra; e,
quando \(r=0\) não há relação linear entre as variáveis consideradas.

Exemplo: onsidere as medidas obtidas de duas variáveis no quadro abaixo.

Quadro de dados
X	Y
74	139
45	108
48	98
36	76
27	62
16	57

Quadro auxiliar para cálculo do coeficiente de correlação linear (r)
X	Y	x_i ⋅ y_i	x_i²	y_i²
74	139	10286	5476	19321
45	108	4860	2025	11664
48	98	4704	2304	9604
36	76	2736	1296	5776
27	62	1674	729	3844
16	57	912	256	3249
246	540	25172	12086	53458

Assim, sendo \(n=6\) obervações segue-se:

\[\begin{align*} S_{xy} = & \sum_{i=1}^{n} x_{i}y_{i} - \frac{\sum_{i=1}^{n}x_{i}\cdot\sum_{i=1}^{n}y_{i}}{n} \\ = & 25172 - \frac{246 \cdot 540}{6} \\ = & 3032 \\ S_{xx} = & \sum_{i=1}^{n} x_{i}^{2} - \frac{(\sum_{i=1}^{n} x_{i})^{2}}{n} \\ = & 12086 - \frac{246^2}{6} \\ = & 2000 \\ S_{yy} = & \sum_{i=1}^{n}y_{i}^{2} - \frac{(\sum_{i=1}^{n} y_{i})^{2}}{n} \\ = & 53458 - \frac{540^2}{6} \\ = & 4858 \end{align*}\]

Portanto:

\[\begin{align*} r = & \frac{{s}_{xy}}{\sqrt{{s}_{xx}\cdot {s}_{yy}}} \\ = & \frac{3032}{\sqrt{2000 \cdot 4858}} \\ = & 0,9727 \end{align*}\]