9.3 Distribuição das médias amostrais e seus intervalos de confiança

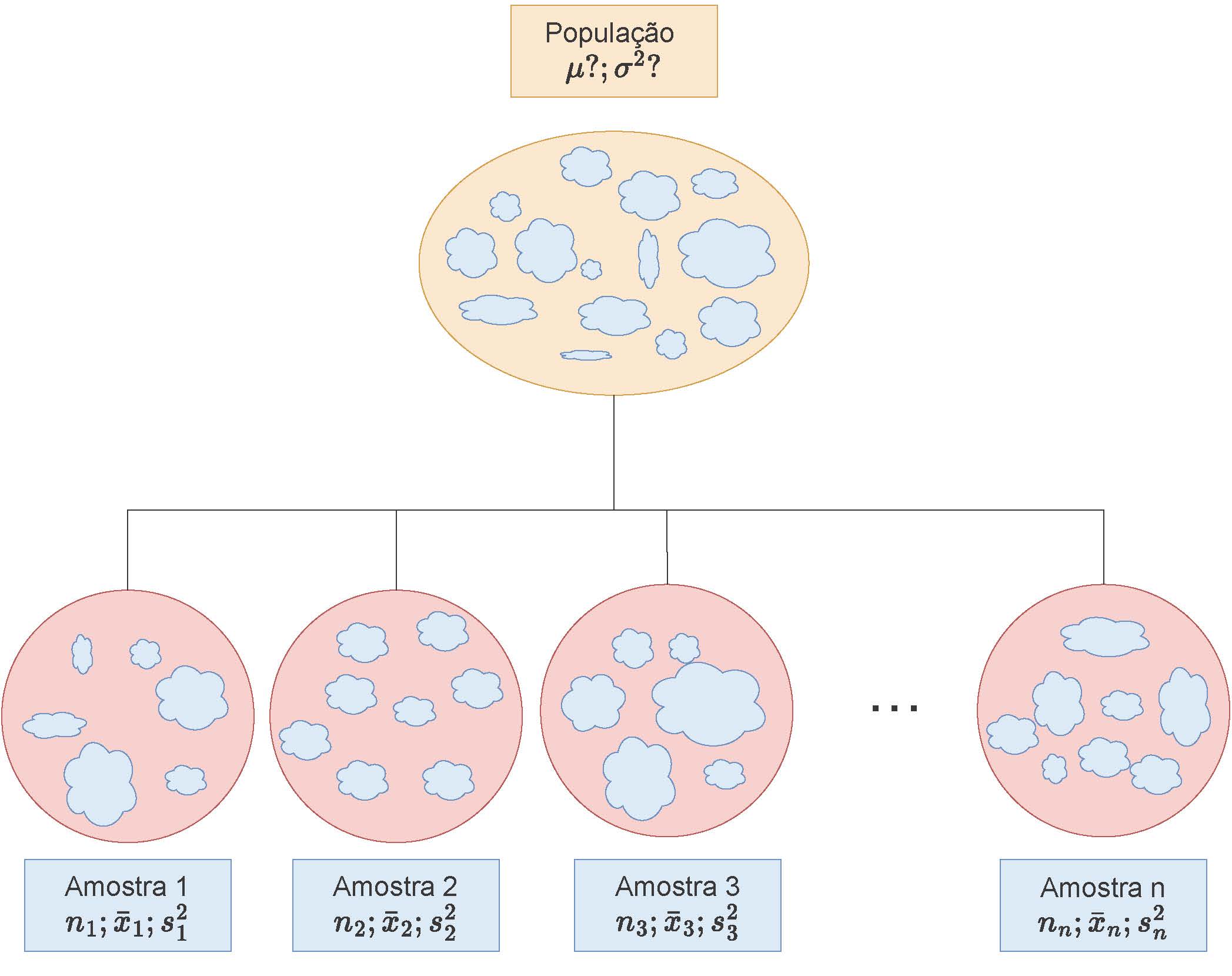
Figure 9.2: Ilustração esquemática de \(n\) amostras extraídas de uma mesma população de parâmetros \(\mu\) e \(\sigma\), cada uma apresentando as respectivas estatísticas calculadas

Para estudarmos a distribuição das médias amostrais considerem uma população com parâmetros \(\mu\) (média) e \(\sigma^{2}\) (variância).

A distribuição das médias amostrais expressa como se distribuem os valores dessa estatística calculada para todas as possíveis amostras de tamanho n extraídas de uma população cujo valor desse parãmetro é desconhecido.

 

A convergência da forma de distribuição e dos parâmetros da distribuição das médias amostrais são elucidadas pelas Leis (fraca e forte) dos Grandes Números e pelo Teorema Central do Limite (George Pólya, 1920).

De acordo com a teoria, pelo uso de simulações computacionais consegue-se ilustrar que para uma amostra de tamanho n (onde \(x_{1},x_{1},...,x_{n}\) são os valores assumidos das variáveis aleatórias \(X_{1},X_{1},...,X_{n}\)) em amostras extraídas de uma população infinita de tamanho N com média \(\mu\) e variância \(\sigma^{2}\)) a distribuição das médias amostrais (v.a. \(\stackrel{-}{X}\)) segue uma distribuição com os média \(=\mu\) e variância \(=\frac{\sigma^{2}}{n}\) pois:

\[\begin{align*} E(\stackrel{-}{X}) & = \frac{1}{n} \cdot \{E(X_{1})+E(X_{2})+...+E(X_{n})\} \\ & = (\frac{1}{n})\cdot\{\mu+\mu+...+\mu\} = \frac{n\cdot\mu}{n} = \mu \end{align*}\]

\[\begin{align*} Var(\stackrel{-}{X}) & = \frac{1}{n^{2}} \cdot \{Var(X_{1})+Var(X_{2}+...+Var(X_{n})\} \\ & = (\frac{1}{n^{2}}) \cdot \{\sigma^{2}+\sigma^{2}+...+\sigma^{2}\} = n \cdot \frac{\sigma^{2}}{n^{2}} = \frac{\sigma^{2}}{n} \end{align*}\]

Equivale afirmar que, independentemente da forma de distribuição da população de origem da qual são extraídas as amostras, a distribuição dos valores da variável aleatória \(\stackrel{-}{X}\) tenderá a seguir uma distribuição \(\sim N(\mu;\frac{\sigma^{2}}{n}\)) à medida que n , o tamanho da amostra aumenta, como ilustrado nas Figuras 9.3 e 9.5.

O TCL garante a aproximação da distribuição de \(\stackrel{-}{X}\) a uma distribuição Normal com média \(\mu\) e variância \(\frac{\sigma^{2}}{n}\) quando \(n\) é grande, independentemente da distribuição da população de origem. Na prática, essa aproximação é usada quando \(n\ge 30\).

Portanto, para populações infinitas ou amostragem com reposição:

\[ \stackrel{-}{X} \sim N(\mu, \frac{\sigma^{2}}{n}) \]

Demostração usando amostras extraídas de uma população com distribuição \(\sim U (v_{min}; v_{max})\)

# Definindo os parãmetros e a amostra
min_1=2
max_1=6
NN=5000
pop_1=runif(NN, min=min_1, max=max_1)
df=as.data.frame(pop_1)

# A distribuição da população ilustrada em um histograma
ggplot(df, aes(x=pop_1)) + 
  geom_histogram( binwidth=1,color="black", fill="lightblue")+
  scale_y_continuous(name="Frequência") +
  scale_x_continuous(name="Valores")+
  labs(title= paste("Histograma de uma população com Distribuição Uniforme"), 
       subtitle = paste("Parâmetros: valor min =",min_1,"; valor max =", max_1))+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))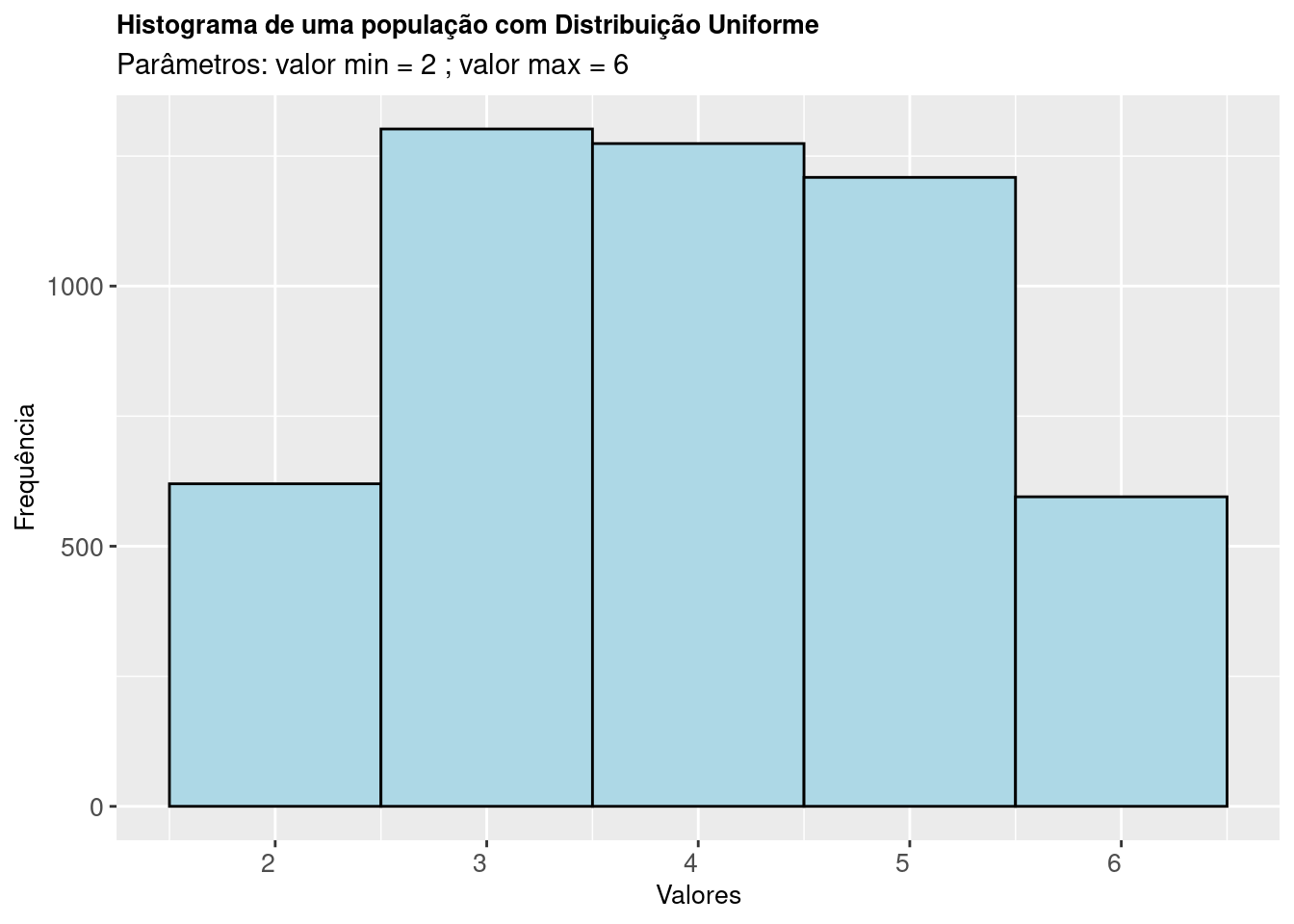

Figure 9.3: Histograma de uma população cuja característica de interesse segue uma Distribuição Uniforme

A Figura 9.3 mostra o histograma de uma amostra de 5000 elementos de uma população com Distribuição Uniforme de parâmetros \(v_{min}:\) 2 e \(v_{max}:\) 6.

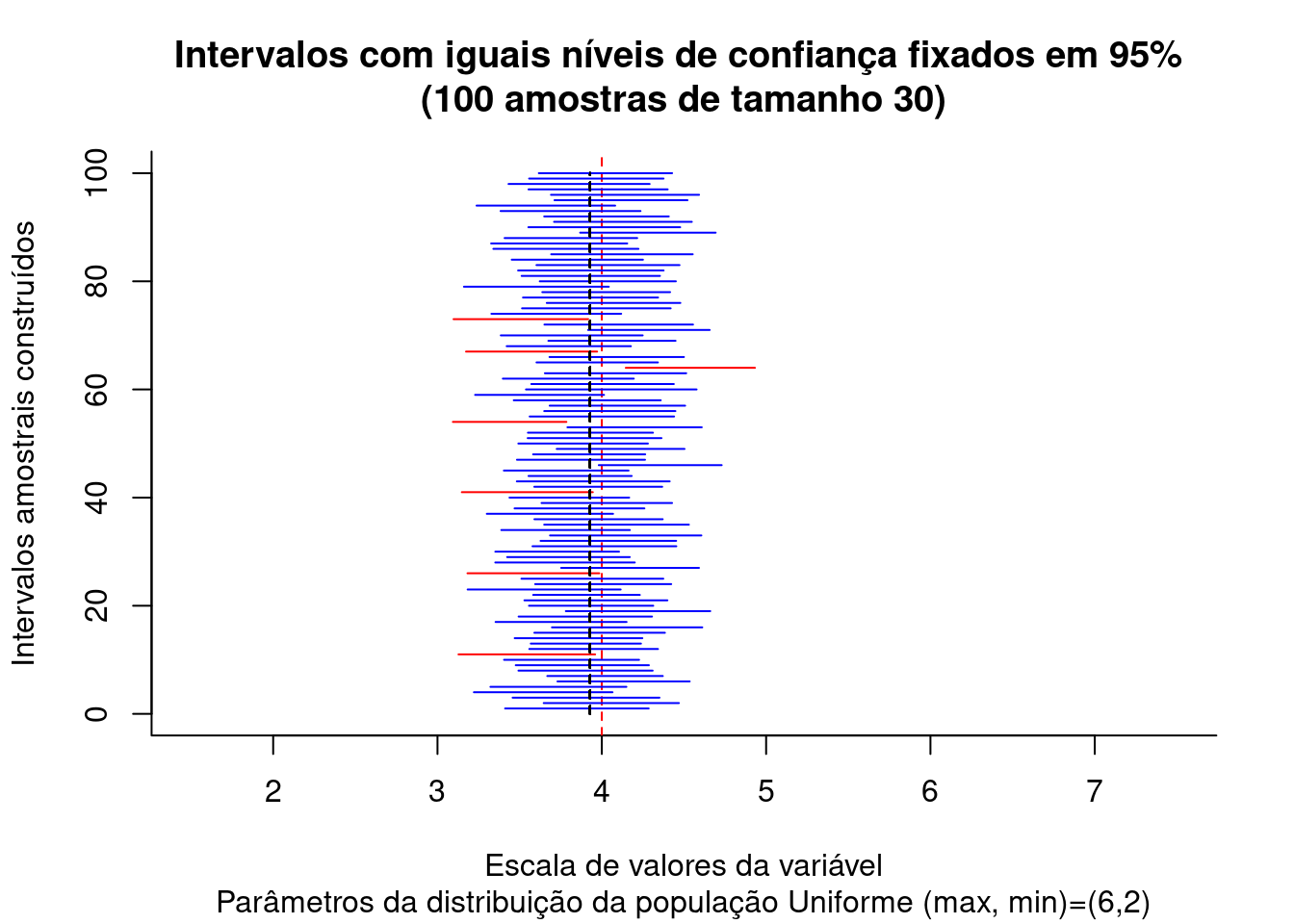
Figure 9.4: Intervalos de confiança construídos para diversas estimativas amostrais de uma população com Distribuição \(\sim N (\mu= \frac{max-min}{2}; \sigma^2=\frac{1}{12}(max-min)^2)\)

A Figura 9.4 expõe os intervalos sob nível de confiança de \((1-\alpha)\)=95% produzidos para as 100 médias de amostras de tamanho 30 extraídas de uma população Uniforme com parâmetros \(v_{max}:\) 6 e \(v_{min}:\) 2 e, conforme assegura o TCL, o valor médio das médias amostrais (linha tracejada preta) converge assintoticamente para a média da população de origem (linha tracejada em vermelho) com o incremento do tamanho das amostras.

meu_titulo1=paste("Distribuição das médias de", N, "amostras de tamanho n=",n,"\n população de origem sob Dist. Unif. (min: ", min_1, "; max: ", max_1, ")")
meu_titulo2=paste("As médias amostrais ~ N( x=",round(mean(m),2),";sd=",round(sd(m),2),")")

dados=as.data.frame(m)
ggplot(dados, aes(m)) +     
  geom_histogram(aes(y = stat(density)), bins=10, fill="lightblue", col="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            args = list(mean=mean(m), sd=sd(m)),
            fill = NA, 
            colour="red") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores das médias amostrais") +
  labs(title=meu_titulo1)+
  geom_segment(aes(x = mean(m), y = 0, xend = mean(m), yend = max(dnorm(m))), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=mean(m), y=max(dnorm(m)),
           label=meu_titulo2, angle=0, vjust=-0.5, hjust=0.5, color="blue",size=6)+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))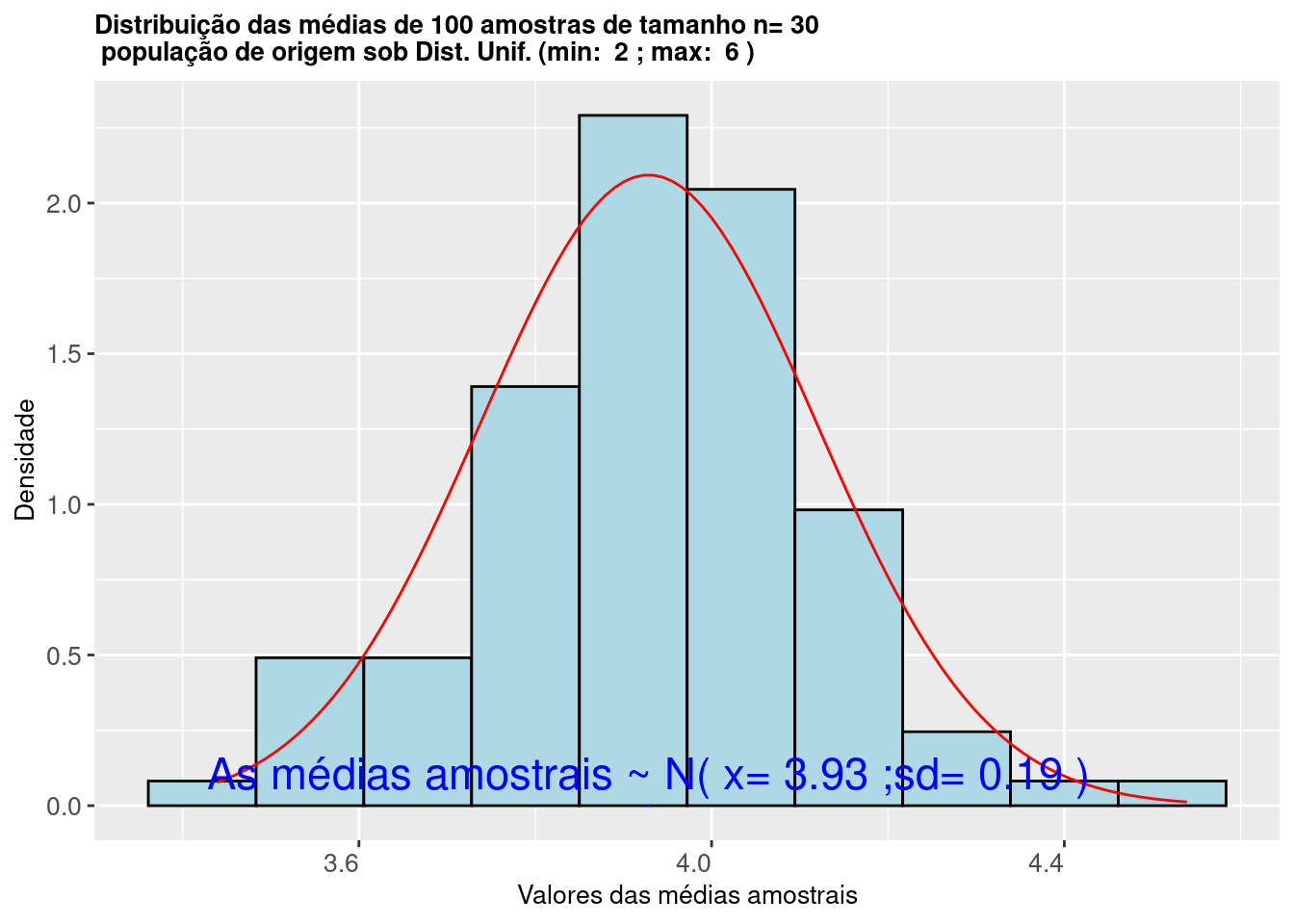

Figure 9.5: Histograma da distribuição das médias de amostras extraidas de uma população com Distribuição Uniforme mostra que as mesmas seguem uma Distribuição \(\sim N (\mu= \frac{max-min}{2};\sigma^2=\frac{1}{12}(max-min)^2)\)

O histograma da Figura 9.5 ilustra que os valores das médias calculadas de 30 amostras extraídas de uma população com distribuição Uniforme \(\sim U (v_{min}, v_{max}\)) seguem uma distribuição Normal \(\sim N (\mu= \frac{v_{max}-v_{min}}{2}; \sigma^2=\frac{1}{12}(v_{max}-v_{min})^2)\).

Demostração usando amostras extraídas de uma população com distribuição \(\sim N (\mu;\sigma)\)

# Definindo os parãmetros e a amostra
media=80
desvio=4
NN=5000
pop_2=rnorm(n=NN, mean = media, sd = desvio)

df=as.data.frame(pop_2)

# A distribuição da população ilustrada em um histograma
ggplot(df, aes(x=pop_2)) + 
  geom_histogram( binwidth=1,color="black", fill="lightblue")+
  scale_y_continuous(name="Frequêcia") +
  scale_x_continuous(name="Valores")+
  labs(title= paste("Histograma de uma população com Distribuição Normal"), 
       subtitle = paste("Parâmetros: média =",media,"; desv. padrão =", desvio))+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))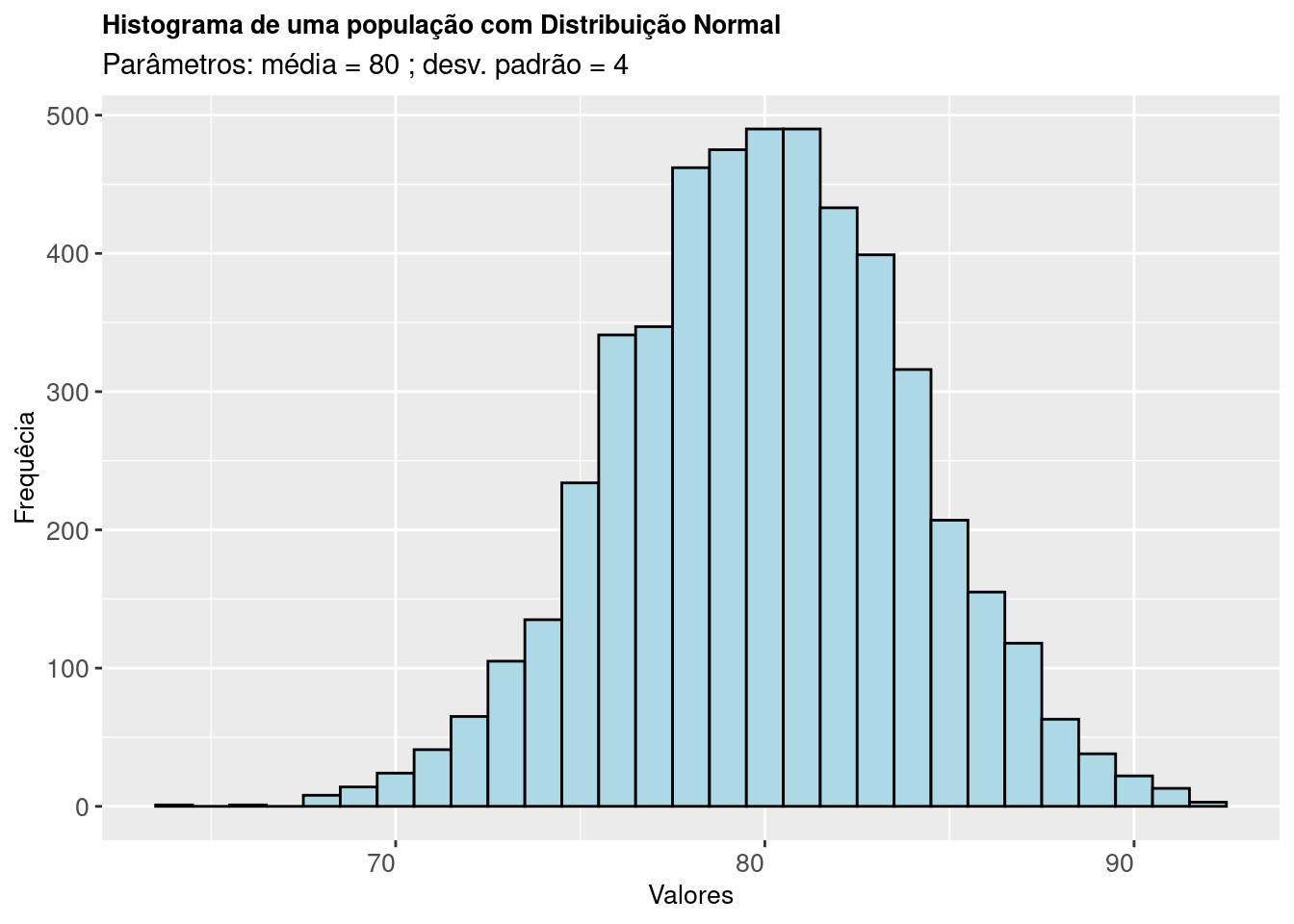

Figure 9.6: Histograma de uma população cuja característica de interesse segue uma Distribuição Normal

A Figura 9.6 mostra o histograma de uma amostra de 5000 elementos de uma população com Distribuição Normal de parâmetros média= 80 e desvio padrão =4.

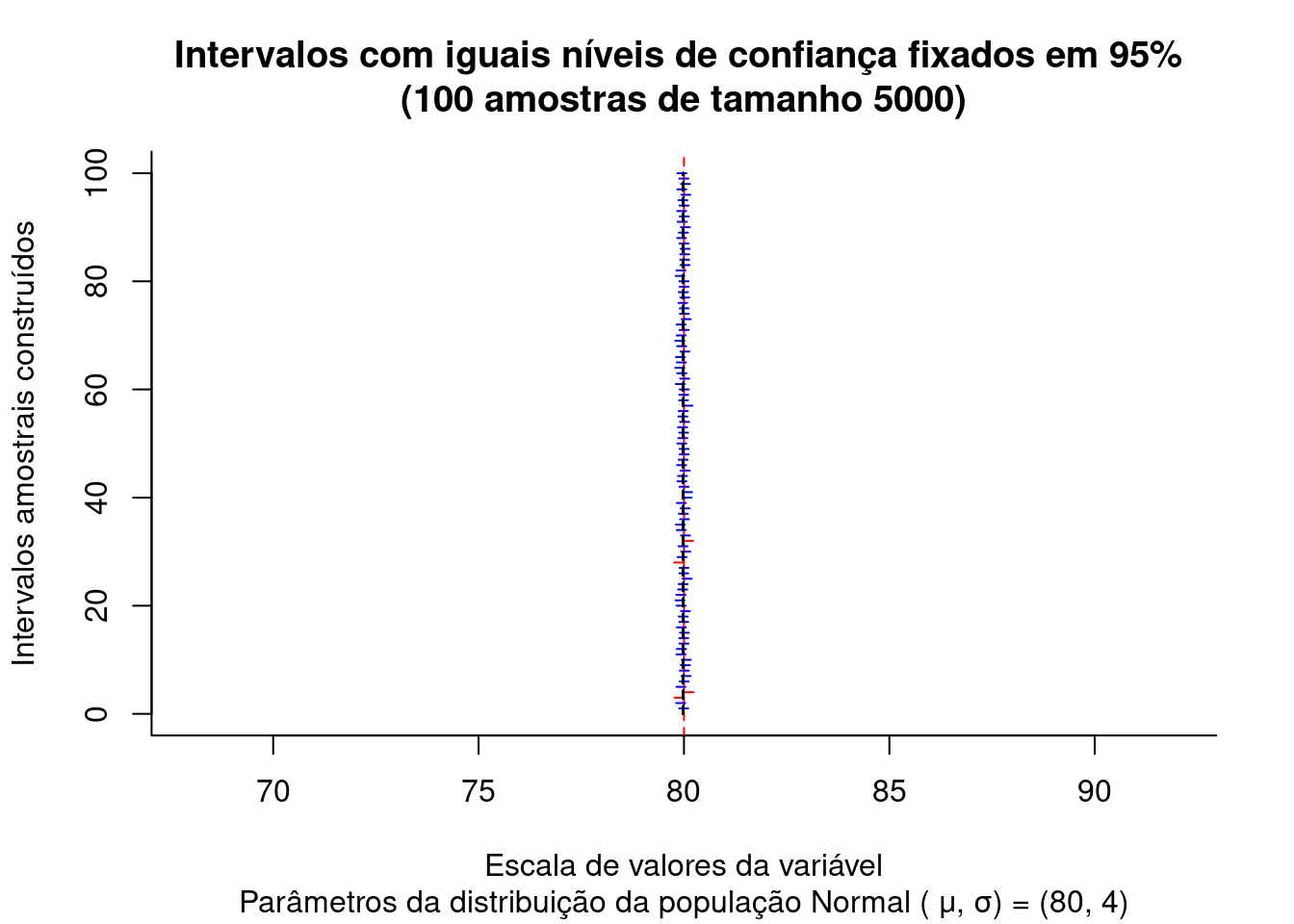
Figure 9.7: Intervalos de confiança construídos para diversas estimativas amostrais de uma população com Distribuição \(\sim N (\mu; \sigma)\)

A Figura 9.7 expõe os intervalos sob nível de confiança de \((1-\alpha)\)=95% produzidos para as 100 médias de amostras de tamanho 5000 extraídas de uma população Uniforme com parâmetros \(v_{max}:\) 6 e \(v_{min}:\) 2 e, conforme assegura o TCL, o valor médio das médias amostrais (linha tracejada preta) converge assintoticamente para a média da população de origem (linha tracejada em vermelho) com o incremento do tamanho das amostras.

meu_titulo1=paste("Distribuição das médias de", N, "amostras de tamanho n=",n,"\n população de origem sob Dist. Normal ( \u03bc: ", media, ", \u03c3: ", desvio, ")")
meu_titulo2=paste("As médias amostrais ~ N( x\u0304=",round(mean(m),2),";sd=",round(sd(m),2),")")

dados=as.data.frame(m)
ggplot(dados, aes(m)) +     
  geom_histogram(aes(y = stat(density)), bins=10, fill="lightblue", col="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            args = list(mean=mean(m), sd=sd(m)),
            fill = NA, 
            colour="red") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores das médias amostrais") +
  labs(title=meu_titulo1)+
  geom_segment(aes(x = mean(m), y = 0, xend = mean(m), yend = max(dnorm(m))), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=mean(m), y=max(dnorm(m)),
           label=meu_titulo2, angle=0, vjust=-0.5, hjust=0.5, color="blue",size=6)+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))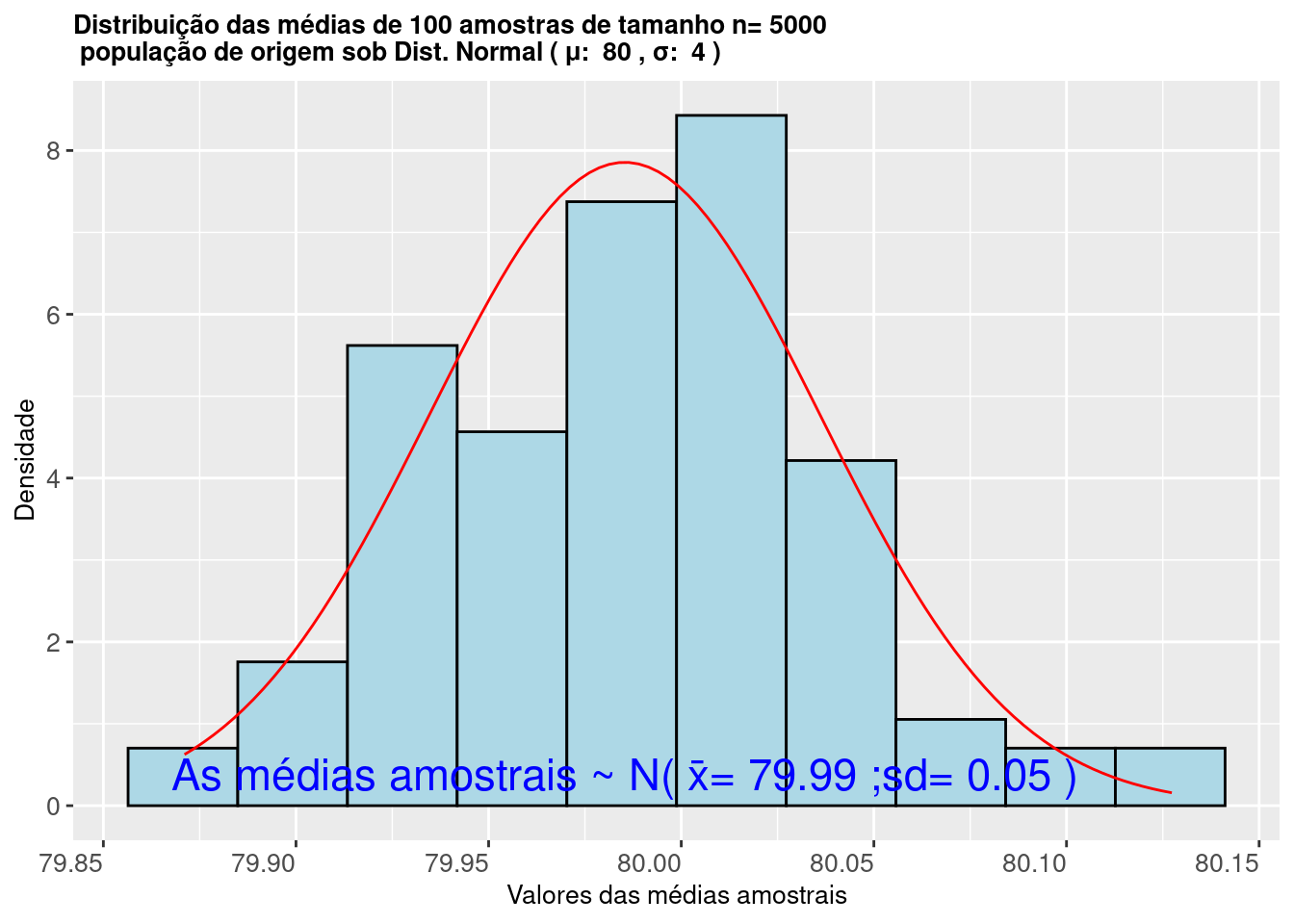

Figure 9.8: Histograma da distribuição das médias de amostras extraidas de uma população Normal mostra que as mesmas seguem uma Distribuição \(\sim N (\stackrel{-}{x}= \mu; s=\frac{\sigma}{\sqrt{n}})\)

O histograma da Figura 9.8 ilustra que os valores das médias calculadas de 5000 amostras extraídas de uma população com distribuição Normal \(\sim N (\mu, \sigma)\) seguem uma distribuição Normal \(\sim N (\mu= \mu; \sigma=\frac{\sigma}{\sqrt{n}})\).

Sendo o erro amostral expresso como: \(\varepsilon=\stackrel{-}{X} - \mu\), o histograma abaixo ilustra que os valores dos erros calculados de 5000 amostras extraídas de uma população com distribuição Normal \(\sim N (\mu, \sigma)\) seguem uma distribuição Normal \(\sim N (\mu= \mu; \sigma=\frac{\sigma}{\sqrt{n}})\).

N=100
n=50
mu=80
sigma=4 
conf=0.95
matriz=IC.Na(N, n, mu, sigma, conf)

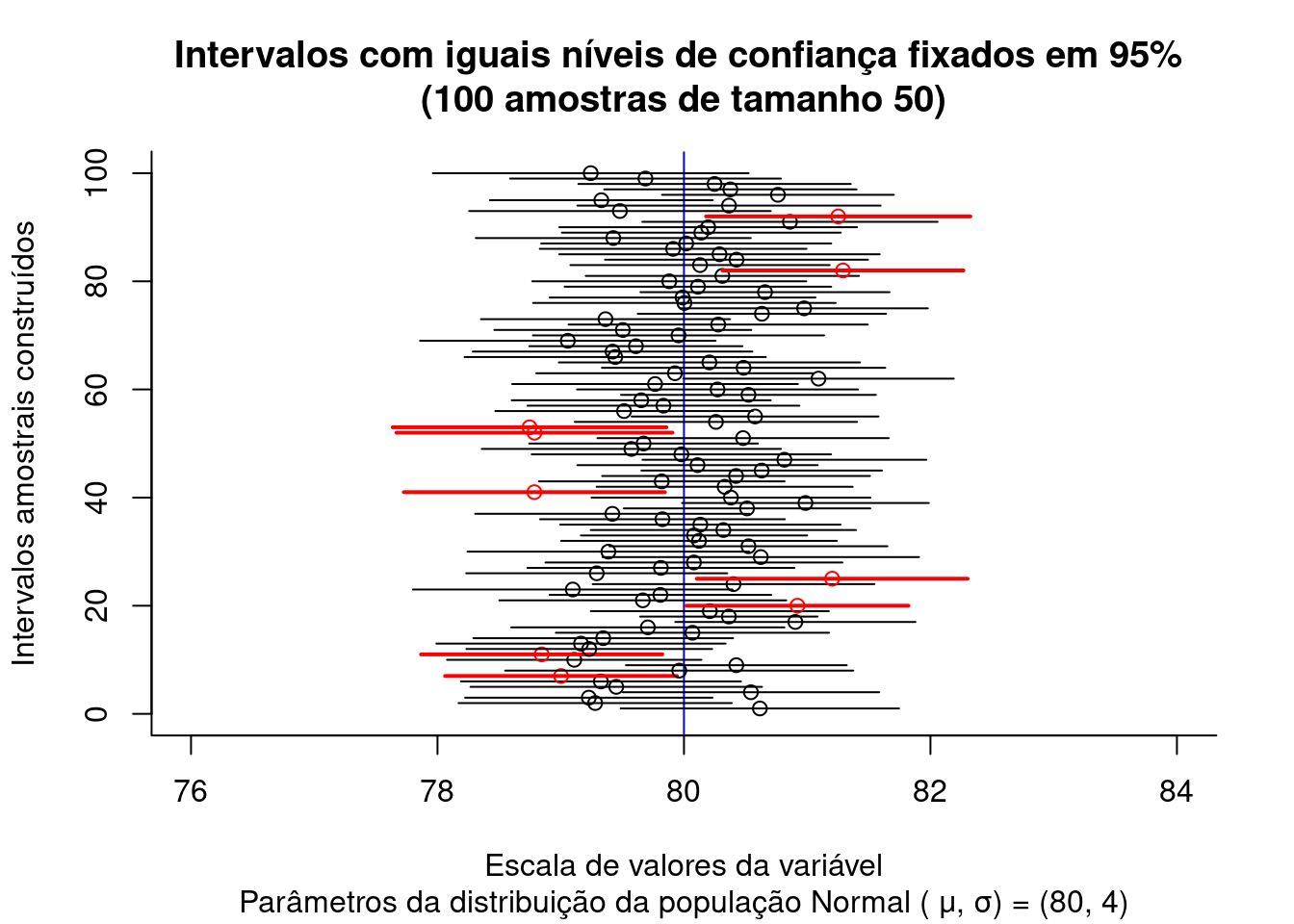
Figure 9.9: Histograma da distribuição dos erros de amostras de tamanho n, extraidas de uma população com distribuição \(\sim N(\mu; \sigma)\) mostra que os mesmos seguem uma distribuição \(\sim N (0; s=\frac{\sigma}{\sqrt{n}})\)

erro_min=min(matriz$erro)
erro_max=max(matriz$erro)


meu_titulo1=paste("Distribuição dos erros de", N, "amostras de tamanho n=",n,"\n extraídas de uma população Normal ( \u03bc: ", mu, ", \u03c3: ", sigma, ")")
meu_titulo2=paste("Os erros amostrais ~ N( x\u0304=",round(mean(matriz$erro),2),"~0 ; sd=",round(sd(matriz$erro),2)," ~\u03c3/sqrt(n))")

ggplot(matriz, aes(x=erro)) + 
  geom_histogram(aes(y = stat(density)), bins=round(sqrt(N),0), fill="lightblue", col="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            args = list(mean=mean(matriz$erro), sd=sd(matriz$erro)),
            fill = NA, 
            colour="red") +
  scale_y_continuous(name="Frequência") +
  scale_x_continuous(name="Valores dos erros amostrais", limits=c(-2,2) )+
  labs(title=meu_titulo1)+
  annotate(geom="text", 
           label=meu_titulo2, x=-0.7,y= 0.9,
           angle=0, vjust=-0.5, hjust=0.5,
           color="blue",size=4)+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))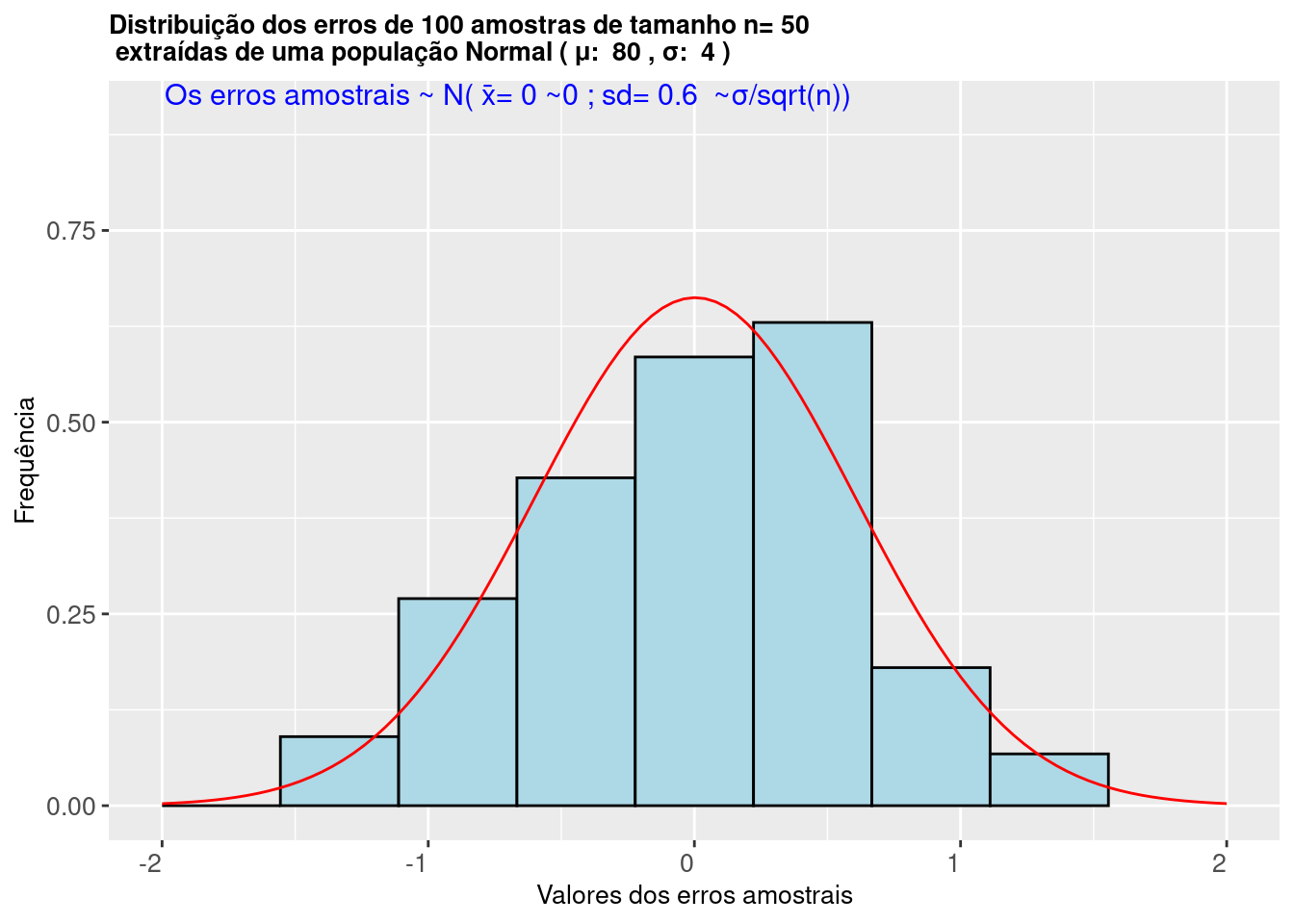

Figure 9.10: Histograma da distribuição dos erros de amostras de tamanho n, extraidas de uma população com distribuição \(\sim N(\mu; \sigma)\) mostra que os mesmos seguem uma distribuição \(\sim N (0; s=\frac{\sigma}{\sqrt{n}})\)

Corolário: se \((X_{1}, X_{2},...,X{n})\) for uma amostra aleatória simples da população \(X\) de média \(\mu\) e variância \(\sigma^{2}\) conhecida, e \(\stackrel{-}{X}= \frac{(X_{1}+X_{2}+...+X{n})}{n}\), tal que \(n\ge 30\), então a estatística \(Z\) pode ser definida, bem como sua correspondente distribuição:

\[ Z = \frac{\stackrel{-}{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0 ,1) \]

Uma vez que a estatística \(Z \sim N(0 ,1)\) (ela ``decorre’’ da padronização da variável aleatória \(\stackrel{-}{X}\)) as probabilidades para os intervalos desejados de valores \(Z\) podem ser facilmente encontrados em tabelas, como mais adiante se verá na constução de intervalos de confiança.

9.3.1 Fator de correção para populações finitas

Se amostras de tamanho \(n\) sem reposição são extraídas de uma população finita de tamanho N aplica-se o fator de correção para populações finitas (\(\sqrt{\frac{(N-n)}{(N-1)}}\)) junto ao desvio padrão das expressões do erro máximo \(\varepsilon\) anteriormente expostas:

\[\begin{align*} \varepsilon & =(\stackrel{-}{x}-\mu)={z}_{(1-\frac{\alpha }{2})} \cdot \frac{\sigma}{\sqrt{n}} \cdot \sqrt{\frac{(N-n)}{(N-1)}} \\ & =(\stackrel{-}{x}-\mu)={z}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}} \cdot \sqrt{\frac{(N-n)}{(N-1)}}\\ & =(\stackrel{-}{x}-\mu)= ({t}_{(1-\frac{\alpha }{2}, (n-1))} \cdot \frac{S}{\sqrt{n}} \cdot \sqrt{\frac{(N-n)}{(N-1)}})\\ \end{align*}\]

Portanto, para populações finitas com amostragem sem reposição (com \(n<N\)):

\[ \stackrel{-}{X} \sim N(\mu, \frac{\sigma^{2}}{n} \cdot \frac{(N-n)}{(N-1)} ) \]

9.3.2 Intervalo de confiança para médias amostrais

Se, por alguma razão, a variância populacional (\(\sigma^{2}\)) é conhecida, podemos utilizar \(\stackrel{-}{X}\) como estimador pontual da média.

Assim, \(X\) seguirá uma distribuição Normal tal que:

 

\[ \stackrel{-}{X} \sim N(\mu, \frac{\sigma^{2}}{n}) \]

Segue também que a estatística \(Z\), como antes definida, seguirá uma distribuição Normal tal que:

 

\[ Z = \frac{\stackrel{-}{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0 ,1) \] com:

• \(\stackrel{-}{X}\) é a média da amostra;
  
• \(\mu\) é a média populacional;
  
• \(\sigma\) é o desvio padrão populacional; e,
  
• \(n\) é o tamanho da amostra extraída.

Entretanto, a situação mais usual é aquela na qual não termos informação alguma sobre a variância populacional (\(\sigma^{2}\)).

Nessas situações, se o tamanho da amostra é grande (na prática \(n\ge 30\)), podemos substituir \(\sigma\) na estatística \(Z\) por \(S\): substituir o desvio padrão populacional pelo desvio padrão da amostra extraída, sem que o erro cometido com esta substituição seja grande.

Com tal substituição, a estatística \(Z\) e passa a ser tal que:

\[ Z = \frac{\stackrel{-}{X} - \mu}{\frac{S}{\sqrt{n}}} \sim N(0 , 1) \]

em que:

• \(\stackrel{-}{X}\) é a média amostral;
  
• \(\mu\) é a média populacional;
  
• \(S\) é o desvio padrão da amostra; e,
  
• \(n\) é o tamanho da amostra.

Caso a variância populacional (\(\sigma^{2}\)) não seja conhecida e o tamanho da amostra não possa ser admitido como grande (\(n<30\)) e sendo o estimador da variância amostral assim definido:

 

\[ {S}^{2}=\frac{1}{\left(n-1\right)}\sum _{i=1}^{n}{\left({X}_{i}-\stackrel{-}{{X}_{1}}\right)}^{2} \]

Definindo-se a variável \(Y = \frac{(n-1)\cdot s^{2}}{\sigma^{2}}\) tem uma distribuição \(\chi^{2}\) com (n-1) graus de liberdade tal que:

 

\[ Y = \frac{(n-1)\cdot s^{2}}{\sigma^{2}} \sim \chi^{2}_{(n-1)}, \]

 

e considerando-se que \(Z\) é tal que:  

\[ Z = \frac{\stackrel{-}{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0 ,1) \]

segue a estatística \(T\) e sua correspondente distribuição, denominada por t de Student :

 

\[ T=\frac{Z}{\sqrt{\frac{Y}{\left(n-1\right)}}} \sim {t}_{\left(n-1\right)}. \]

Para essa situação na qual a variância populacional não é conhecida e o tamanho amostral é pequeno, com alguma manipulação chega-se à estatística \(T\) e sua correspondente distribuição:

 

\[ T = \frac{(\stackrel{-}{X} - \mu)}{ \frac{S}{\sqrt{n}} } \sim t_{(n-1)} \]

em que:

• \(\stackrel{-}{X}\) é a média amostral;
  
• \(\mu\) é a média populacional;
• \(S\) é o desvio padrão da amostra; e,
  
• \(n\) é o tamanho da amostra; e,
  
• \((n-1)\) é uma quantidade denominada como graus de liberdade.

As probabilidades associadas a um intervalo para um determinado valor da estatística ``t’’ da distribuição de Student encontram-se tabeladas para variados graus de liberdade , como mais adiante se verá na constução de intervalos de confiança.

9.3.3 Intervalo de confiança bilateral para uma média amostral sob variância populacional conhecida (Figura 6.9)

 

\[ Z = \frac{\stackrel{-}{X} - \mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0 ,1) \]

 

em que:

• \(\stackrel{-}{X}\) é a média amostral;
  
• \(\mu\) é a média populacional;
  
• \(\sigma\) é o desvio padrão populacional;
• \(n\) é o tamanho da amostra; e,
• \(Z\) é a estatística a ser calculada para a construção do intervalo de confiança sob o nível de significância \(\alpha\) estabelecido.

alfa=0.05

prob_desejada1=alfa/2
z_desejado1=round(qnorm(prob_desejada1),4)
d_desejada1=dnorm(z_desejado1, 0, 1)

prob_desejada2=1-alfa/2
z_desejado2=round(qnorm(prob_desejada2),4)
d_desejada2=dnorm(z_desejado2, 0, 1)



ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``z'' da distribuição Normal padrão")  +
  labs(title= 
         "Curva da função densidade \nDistribuição Normal Padrão", 
       subtitle = "P(-z, z)=(1-\u03b1) em cinza (nível de confiança) \nP(-\U221e; -z)= P(z; \U221e)= \u03b1/2 em vermelho ")+
  geom_segment(aes(x = z_desejado1, y = 0, xend = z_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = z_desejado2, y = 0, xend = z_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_desejado1-0.1, y=d_desejada1, label="-z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado2+0.3, y=d_desejada2, label="z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado1-1.8, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.5, y=0.1, label="Intervalo aberto à dir. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Intervalo fechado \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()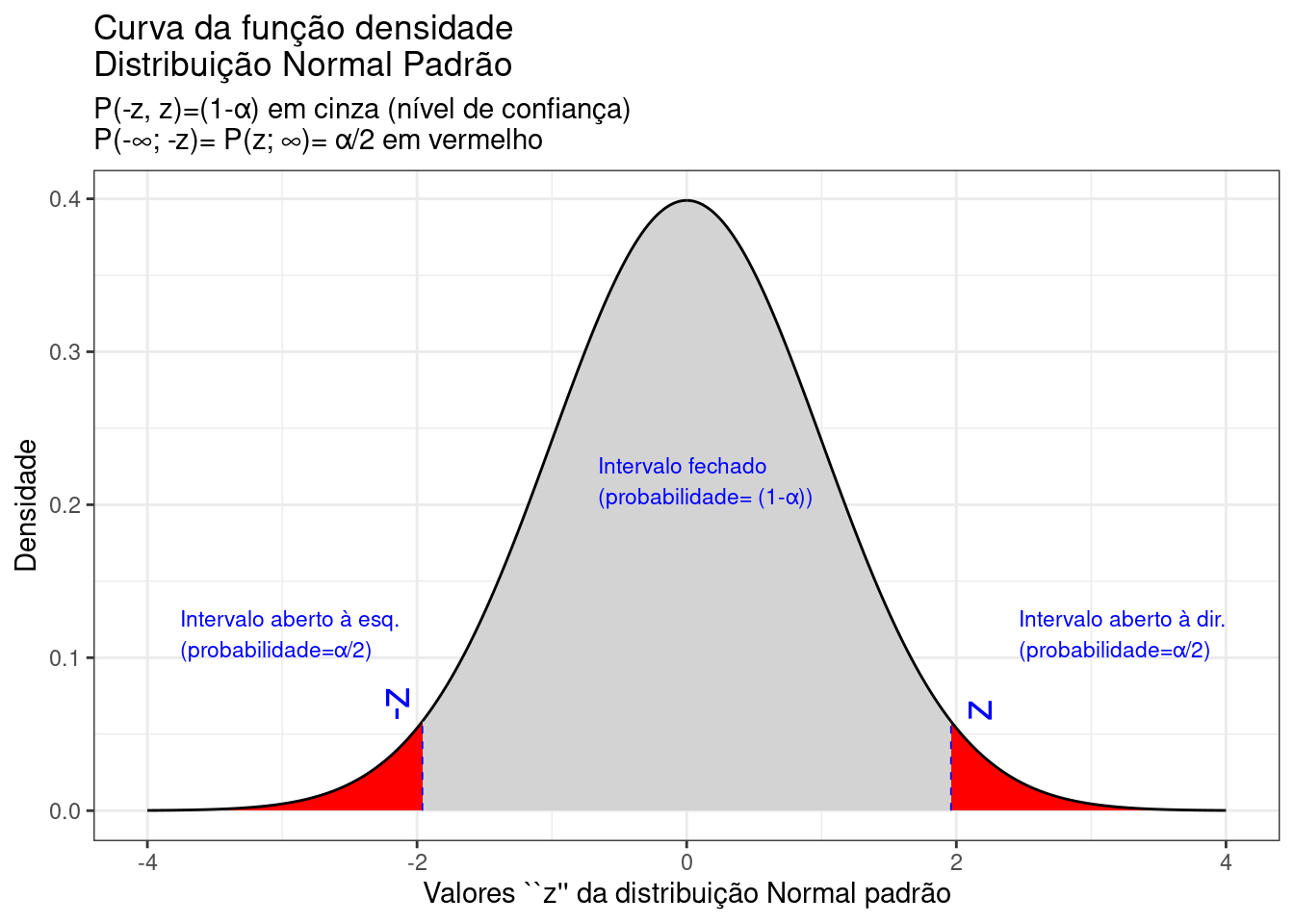

Figure 9.11: Regiões críticas, aquém e além das quais, a probabilidade associada aos valores \(Z\) é inferior a \(\frac{\alpha}{2}\), estabelecendo assim um intervalo com nível de confiança igual a \((1-\alpha)\)

Na Figura 9.11 observa-se:

 

• o nível de significância \(\alpha\);
  
• o nível de confiança \((1-\alpha)\); e,
  
• o valor tabelado da estatística \(Z(z)\) para o nível de confiança fixado.

Assim,

\[\begin{align*} P\left[-{Z}_{(1-\frac{\alpha }{2})}\le Z \le {Z }_{(1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P\left[-{z}_{(1-\frac{\alpha }{2})}\le \frac{\stackrel{-}{x}-\mu }{\frac{\sigma}{\sqrt{n}}} \le {z}_{(1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P[\stackrel{-}{x}-({z}_{(1-\frac{\alpha }{2})} \cdot \frac{\sigma}{\sqrt{n}}) \le \mu \le \stackrel{-}{x}+({z}_{(1-\frac{\alpha }{2})} \cdot \frac{\sigma}{\sqrt{n}}) ] & = (1-\alpha) \end{align*}\]

\[ IC(\mu)_{(1-\alpha)} = [\stackrel{-}{x} \pm {z}_{c} \cdot \frac{\sigma}{\sqrt{n}}] \]

Assim, se \(\stackrel{-}{x}\) é usado como estimativa de \(\mu\), podemos afirmar estar \(100.(1-\alpha)\)% confiantes de que o erro não excederá \(({z}_{(1-\frac{\alpha }{2})} \cdot \frac{\sigma}{\sqrt{n}})\).

 

A quantidade \(\varepsilon=(\stackrel{-}{x}-\mu)={z}_{(1-\frac{\alpha }{2})} \cdot \frac{\sigma}{\sqrt{n}}\) é chamada de Erro máximo da estimativa ao se arbitrar um nível de confiança \(\alpha\) para um determinado tamanho amostral.

Exemplo: As vendas de 15 lojas de uma região do país apresentam uma média igual a US$ 20.000,00. Sabendo-se que as vendas de todas as lojas da região é uma variável aleatória que segue uma distribuição Normal, com desvio padrão igual a US$ 8.300,00, construa o intervalo de confiança para a média ao nível de confiança de 95%.

Dados do problema:

 

• o tamanho da amostra: \(n=15\);
  
• a média amostral: \(\stackrel{-}{x}\) = US$ 20.000;
  
• o desvio padrão populacional: \(\sigma\)= US$ 8.300;
  
• nível de confiança: \((1-\alpha) = 0,95\); e,
• valor extraído da tabela \(z=1,96\) correspondente ao nível de confiança estipulado \((1-\alpha)=95\%\).

\[\begin{align*} P[\stackrel{-}{x}-({z}_{(1-\frac{\alpha }{2})} \cdot \frac{\sigma}{\sqrt{n}}) \le \mu \le \stackrel{-}{x}+({z}_{(1-\frac{\alpha }{2})} \cdot \frac{\sigma}{\sqrt{n}}) ] & = (1-\alpha) \\ P[20.000 - (1,96 \cdot \frac{8.300}{\sqrt{15}}) \le \mu \le 20000 + ( 1,96 \cdot \frac{8.300}{\sqrt{15}}) ] & = 0,95 \\ P[20.000 - 4.200,38 \le \mu \le 20.000 + 4.200,38 ] & = 0,95 \\ \end{align*}\]

\[ IC_{(1-\alpha=0,95)} = [US\$ 15.799,62; US\$ 24.200,38] \]

Se quisermos ser rigorosos na interpretação do intervalo de confiança calculado podemos explicar que, se extrairmos um grande número de amostras de tamanho 15 dessa população, e para todas elas calcularmos intervalos de confiança como o acima definido, a proporção desses intervalos onde poderemos encontrar a média populacional de vendas será de 0,95 (95 intervalos em 100).

De uma forma mais sintética, podemos afirmar que o intervalo aleatório ]US$ 15.799,62; US$ 24.200,38[, é um intervalo de confiança a 95% para a média de vendas.

De forma mais corrente, embora menos correta em termos teóricos, é usual afirmar que, com 95% de confiança a média de vendas se situa entre os valores US$ 15.799,62 e US$ 24.200,38.

Intervalos de confiança unilaterais para uma média amostral sob variância populacional conhecida.

A Figura 6.10 ilustra um intervalo de confiança unilateral limitado à direita por um valor máximo, dde tal sorte que a probabilidade associada ao intervalo de valores da estatística \(Z\) inferiores a esse limitante é

\[ P\left [\mu \le \bar{x} + {z}_{c} \cdot \frac{\sigma}{\sqrt{n}} \right ] = (1- \alpha) \]

prob_desejada=0.95
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)

ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(-4, 0),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``z'' da distribuição Normal padrão")  +
  geom_area(stat = "function",
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado),
            colour="black")+
  geom_area(stat = "function",
            fun = dnorm, 
            fill = "red", 
            xlim = c( z_desejado, 4),
            colour="black")+
  labs(title= 
      "Curva da função densidade
      \nDistribuição Normal Padrão", 
      subtitle = "P(-\U221e; z)=(1-\u03b1) em cinza (nível de confiança)  \nP(z, + \U221e)= \u03b1, em vermelho ")+
  annotate(geom="text", x=z_desejado1+3.5, y=d_desejada1, label="z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado1+4.5, y=0.1, label="Intervalo aberto à dir. \n(probabilidade=\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Intervalo aberto à esq. \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()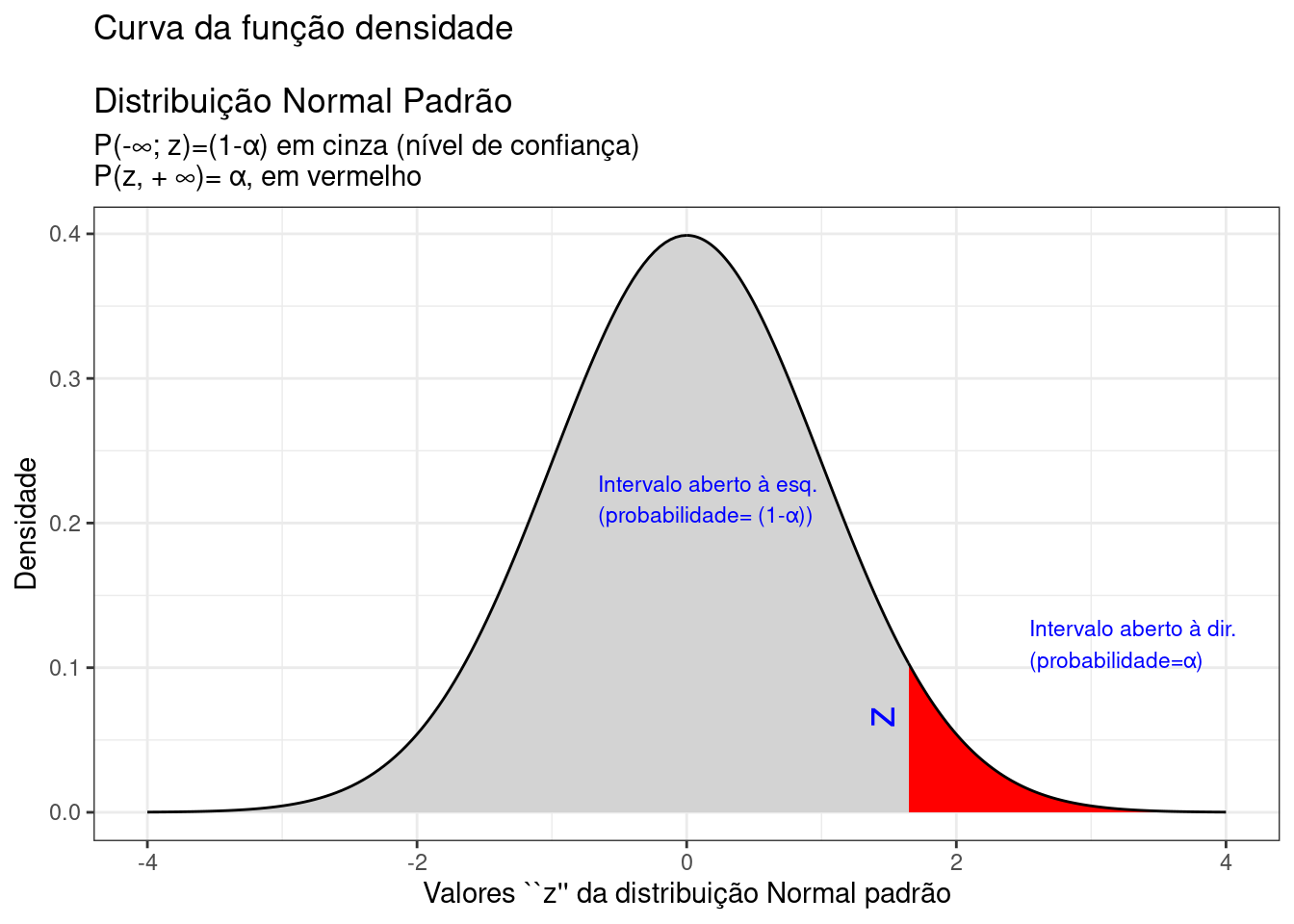

Figure 9.12: Região crítica, além da qual, a probabilidade associada aos valores \(Z\) é inferior a \(\alpha\), delimitando assim, à esquerda, um intervalo aberto com nível de confiança igual a \((1-\alpha)\)

A Figura 9.13 ilustra um intervalo de confiança unilateral limitado à esquerda por um valor mínimo, de tal sorte que a probabilidade associada ao intervalo de valores da estatística \(Z\) superiores a esse limitante é

\[ P\left [\mu \ge \bar{x} - {z}_{c} \cdot \frac{\sigma}{\sqrt{n}} \right ] = (1- \alpha) \]

prob_desejada=0.05
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)

ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(-4, 0),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``z'' da distribuição Normal padrão")  +
  geom_area(stat = "function",
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado),
            colour="black")+
  geom_area(stat = "function",
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c( z_desejado, 4),
            colour="black")+
  labs(title= 
      "Curva da função densidade
      \nDistribuição Normal Padrão", 
      subtitle = "P(-\U221e; z)=\u03b1, em vermelho \nP(z, + \U221e)= (1-\u03b1) em cinza")+
  annotate(geom="text", x=z_desejado1+0.5, y=d_desejada1, label="-z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado1-2, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Intervalo aberto à dir. \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()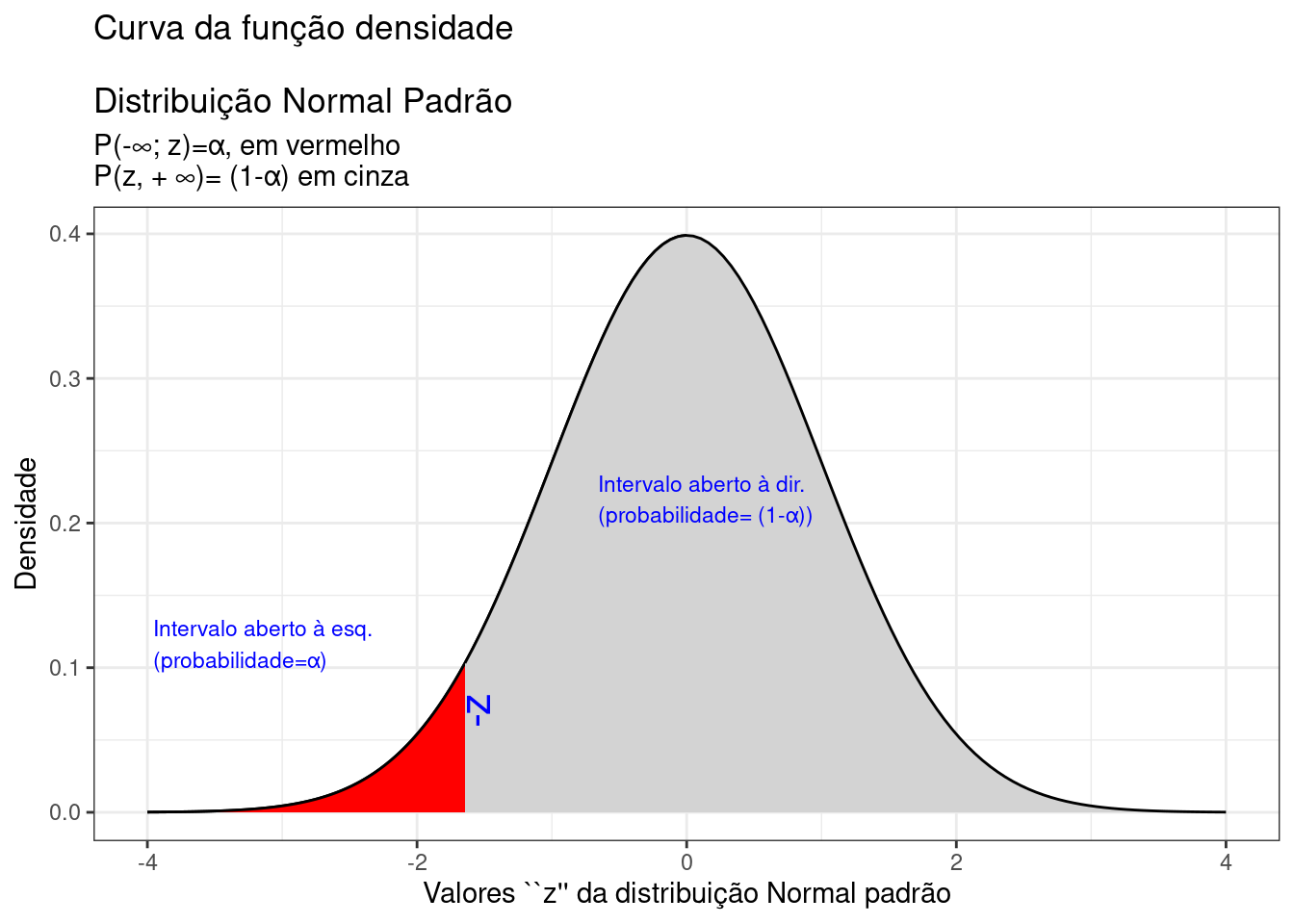

Figure 9.13: Região crítica, aquém da qual, a probabilidade associada aos valores \(Z\) é inferior a \(\alpha\), delimitando assim, à direita, um intervalo aberto com nível de confiança igual a \((1-\alpha)\)

9.3.4 Intervalo de confiança para uma média amostral sob variância populacional desconhecida mas amostras não tão pequenas: \(n \ge 30\) (Figura 9.14)

 

\[ Z = \frac{\stackrel{-}{X} - \mu}{\frac{S}{\sqrt{n}}} \sim N(0 , 1) \]

 

em que:

• \(\stackrel{-}{X}\) é a média amostral;
  
• \(\mu\) é a média populacional;
  
• \(S\) é o desvio padrão amostral;
• \(n\) é o tamanho da amostra; e,
• \(Z\) é a estatística a ser calculada para a construção do intervalo de confiança sob o nível de significância \(\alpha\) estabelecido.

alfa=0.05

prob_desejada1=alfa/2
z_desejado1=round(qnorm(prob_desejada1),4)
d_desejada1=dnorm(z_desejado1, 0, 1)

prob_desejada2=1-alfa/2
z_desejado2=round(qnorm(prob_desejada2),4)
d_desejada2=dnorm(z_desejado2, 0, 1)




ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``z'' da distribuição Normal padrão")  +
  labs(title= 
         "Curva da função densidade \nDistribuição Normal Padrão", 
       subtitle = "P(-z; z)=(1-\u03b1) em cinza (nível de confiança) \nP(-\U221e; -z)= P(z; \U221e)= \u03b1/2 em vermelho")+
  geom_segment(aes(x = z_desejado1, y = 0, xend = z_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = z_desejado2, y = 0, xend = z_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_desejado1-0.1, y=d_desejada1, label="-z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado2+0.3, y=d_desejada2, label="z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado1-1.8, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.5, y=0.1, label="Intervalo aberto à dir. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Intervalo fechado \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()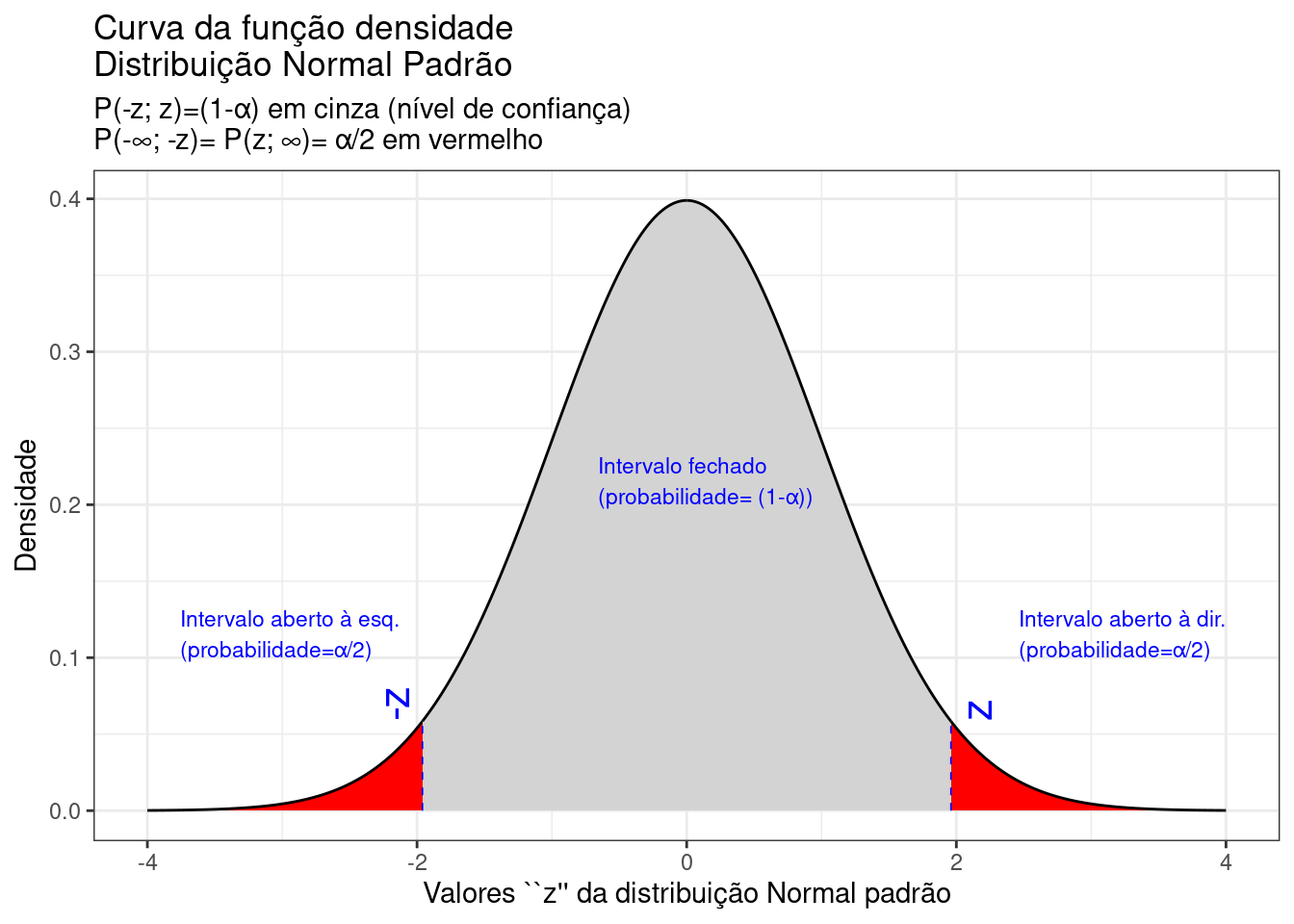

Figure 9.14: Regiões críticas, aquém e além das quais, a probabilidade associada aos valores \(Z\) é inferior a \(\frac{\alpha}{2}\), estabelecendo assim um intervalo com nível de confiança igual a \((1-\alpha)\)

Na Figura 9.14 observa-se:

 

• o nível de significância \(\alpha\);
  
• o nível de confiança \((1-\alpha)\); e,
  
• o valor tabelado da estatística \(Z(z)\) para o nível de confiança fixado.

Assim,

 

\[\begin{align*} P\left[-{Z}_{(1-\frac{\alpha }{2})}\le Z \le {Z }_{(1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P\left[-{z}_{(1-\frac{\alpha }{2})}\le \frac{\stackrel{-}{x}-\mu }{(\frac{S}{\sqrt{n})}} \le {z}_{(1-\frac{\alpha }{2})}\right] & = (1-\alpha) \\ P[\stackrel{-}{x}-({z}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}}) \le \mu \le \stackrel{-}{x}+({z}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}}) ] & = (1-\alpha) \end{align*}\]

\[ IC(\mu)_{(1-\alpha)} = [\stackrel{-}{x} \pm {z}_{c} \cdot \frac{S}{\sqrt{n}} ] \]

Assim, se \(\stackrel{-}{x}\) é usado como estimativa de \(\mu\) podemos afirmar estar \(100(1-\alpha)\)% confiantes de que o erro não excederá \(({z}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}})\).

 

A quantidade \(\varepsilon=(\stackrel{-}{x}-\mu)={z}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}}\) é chamada de Erro máximo da estimativa ao se arbitrar um nível de confiança \(\alpha\) para um determinado tamanho amostral.

Exemplo: As vendas de 60 lojas de uma região do país apresentam uma média igual a US$ 20.000,00 e desvio padrão de US$ 8.300,00. Construa o intervalo de confiança para a média ao nível de confiança de 95%.

Dados do problema:

 

• o tamanho da amostra: \(n=60\);
  
• a média amostral: \(\stackrel{-}{x}=US\$ 20.000\);
  
• o desvio padrão amostral: \(s=US\$ 8.300\);
  
• nível de confiança: \((1-\alpha)=0,95\); e,
• valor extraído da tabela \(z=1,96\) correspondente ao nível de confiança estipulado \((1-\alpha)=95\%\).

\[\begin{align*} P[\stackrel{-}{x}-({z}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}}) \le \mu \le \stackrel{-}{x}+({z}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}}) ] & = (1-\alpha) \\ P[20.000 - (1,96 \cdot \frac{8.300}{\sqrt{60}}) \le \mu \le 20.000 + ( 1,96 \cdot \frac{8.300}{\sqrt{60}}) ] & = 0,95 \\ P[20.000 - 2.100,19 \le \mu \le 20.000 + 2.100,19 ] & = 0,95 \end{align*}\]

\[ IC_{(1-\alpha=0,95)} = [US\$ 17.899,81;US\$ 22.100,19] \]

Se quisermos ser rigorosos na interpretação do intervalo de confiança calculado podemos explicar que se extrairmos um grande número de amostras de tamanho 60 dessa população, e para todas elas calcularmos intervalos de confiança como o acima definido, a proporção desses intervalos onde poderemos encontrar a média populacional de vendas será de 0,95 (95 intervalos em 100).

De uma forma mais sintética, podemos afirmar que o intervalo aleatório ]US$ 17.899,81; US$ 22.100,19[, é um intervalo de confiança a 95% para a média de vendas.

De forma mais corrente, embora menos correta em termos teóricos, é usual afirmar que, com 95% de confiança a média de vendas se situa entre os valores US$ 17.899,81 e US$ 22.100,19.

Intervalos de confiança unilaterais para uma média amostral sob variância populacional desconhecida mas amostras não tão pequenas: \(n \ge 30\).

A Figura 9.15 ilustra um intervalo de confiança unilateral limitado à direita por um valor máximo, de tal sorte que a probabilidade associada ao intervalo de valores da estatística \(Z\) inferiores a esse limitante é

\[ P\left [\mu \le \bar{x} + {z}_{c} \cdot \frac{S}{\sqrt{n}} \right ] = (1- \alpha) \]

prob_desejada=0.95
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)

ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(-4, 0),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``z'' da distribuição Normal padrão")  +
  geom_area(stat = "function",
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado),
            colour="black")+
  geom_area(stat = "function",
            fun = dnorm, 
            fill = "red", 
            xlim = c( z_desejado, 4),
            colour="black")+
  labs(title= 
      "Curva da função densidade
      \nDistribuição Normal Padrão", 
      subtitle = "P(-\U221e; z)=(1-\u03b1) em cinza (nível de confiança)  \nP(z, + \U221e)= \u03b1, em vermelho ")+
  annotate(geom="text", x=z_desejado1+3.5, y=d_desejada1, label="z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado1+4.5, y=0.1, label="Intervalo aberto à dir. \n(probabilidade=\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Intervalo aberto à esq. \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()

Figure 9.15: Região crítica, além da qual, a probabilidade associada aos valores \(Z\) é inferior a \(\alpha\), delimitando assim, à esquerda, um intervalo aberto com nível de confiança igual a \((1-\alpha)\)

A Figura 9.16 ilustra um intervalo de confiança unilateral limitado à esquerda por um valor mínimo, de tal sorte que a probabilidade associada ao intervalo de valores da estatística \(Z\) superiores a esse limitante é

\[ P\left [\mu \ge \bar{x} - {z}_{c} \cdot \frac{S}{\sqrt{n}} \right ] = (1- \alpha) \]

prob_desejada=0.05
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)

ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(-4, 0),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``z'' da distribuição Normal padrão")  +
  geom_area(stat = "function",
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado),
            colour="black")+
  geom_area(stat = "function",
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c( z_desejado, 4),
            colour="black")+
  labs(title= 
      "Curva da função densidade
      \nDistribuição Normal Padrão", 
      subtitle = "P(-\U221e; z)=\u03b1, em vermelho \nP(z, + \U221e)= (1-\u03b1) em cinza")+
  annotate(geom="text", x=z_desejado1+0.5, y=d_desejada1, label="-z", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=z_desejado1-1.5, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Intervalo aberto à dir. \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()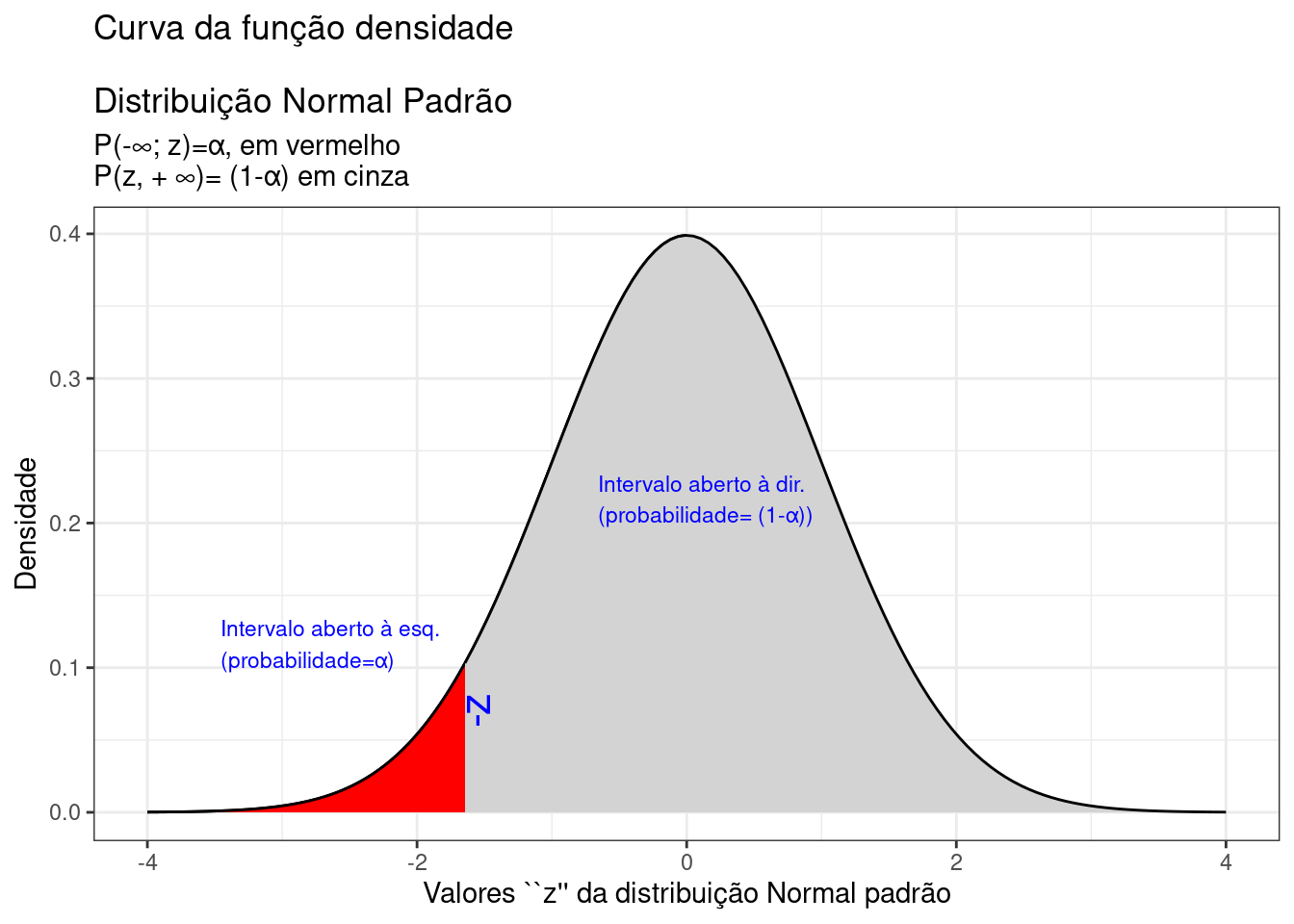

Figure 9.16: Região crítica, aquém da qual, a probabilidade associada aos valores \(Z\) é inferior a \(\alpha\), delimitando assim, à direita, um intervalo aberto com nível de confiança igual a \((1-\alpha)\)

9.3.5 Intervalo de confiança para uma média amostral sob variância populacional desconhecida e amostras de qualquer tamanho (Figura 9.17)

 

\[ T = \frac{(\stackrel{-}{X} - \mu)}{ \frac{S}{\sqrt{n}} } \sim t_{(n-1)} \]

 

em que:

• \(\stackrel{-}{X}\) é a média amostral;
  
• \(\mu\) é a média populacional;
  
• \(S\) é o desvio padrão amostral;
  
• \(n\) é o tamanho da amostra; e,
• \(T\) é a estatística a ser calculada para a construção do intervalo de confiança sob o nível de significância \(\alpha\) estabelecido.

alfa=0.05

prob_desejada1=alfa/2
df=20
t_desejado1=round(qt(prob_desejada1,df ),4)
d_desejada1=dt(t_desejado1,df)

prob_desejada2=1-alfa/2
df=20
t_desejado2=round(qt(prob_desejada2, df),4)
d_desejada2=dt(t_desejado2,df)



ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dt,
            args=list(df), 
            fill = "red", 
            xlim = c(-4, t_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(t_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(0, t_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "red", 
            xlim = c(t_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``t'' da distribuição de Student com gl=n-1")  +
  labs(title= "Curva da função densidade \nDistribuição t ", 
       subtitle = "P(-t; t)=(1-\u03b1) em cinza (nível de confiança) \nP(-\U221e; -t)= P(t; \U221e)= \u03b1/2 em vermelho ")+
  geom_segment(aes(x = t_desejado1, y = 0, xend = t_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = t_desejado2, y = 0, xend = t_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=t_desejado1-0.1, y=d_desejada1, label="-t", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=t_desejado2+0.3, y=d_desejada2, label="t", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=t_desejado1-1.8, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado2+0.5, y=0.1, label="Intervalo aberto à dir. \n(probabilidade=\u03b1/2)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado1+1.3, y=0.2, label="Intervalo fechado \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+  theme_bw()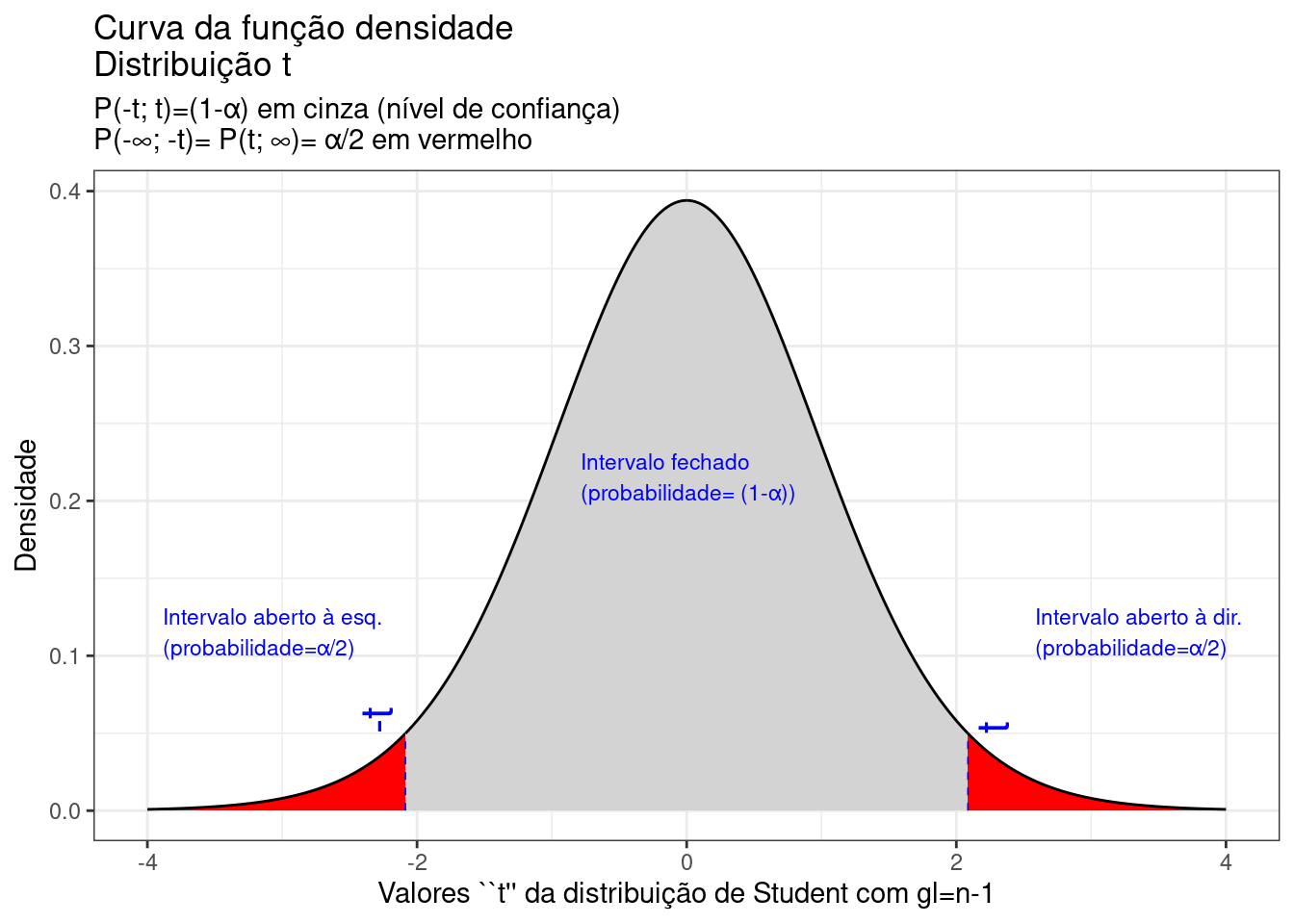

Figure 9.17: Regiões críticas, aquém e além das quais, a probabilidade associada aos valores \(T\) (\((n-1)\) graus de liberdade) é inferior a \(\frac{\alpha}{2}\), estabelecendo assim um intervalo com nível de confiança igual a \((1-\alpha)\)

Na Figura 9.17 observa-se:

 

• o nível de significância \(\alpha\);
  
• o nível de confiança \((1-\alpha)\); e,
  
• o valor tabelado da estatística \(T(t)\) sob \(n-1\) graus de liberdade para o nível de confiança fixado.

Assim,

 

\[\begin{align*} P\left[-{T}_{(1-\frac{\alpha }{2}, (n-1))}\le T \le {T }_{(1-\frac{\alpha }{2}, (n-1))}\right] & = (1-\alpha) \\ P\left[-{t}_{(1-\frac{\alpha }{2}, (n-1))}\le \frac{\stackrel{-}{x}-\mu }{\frac{S}{\sqrt{n}}} \le {t}_{(1-\frac{\alpha }{2}, (n-1))}\right] & = (1-\alpha) \\ P[\stackrel{-}{x}-({t}_{(1-\frac{\alpha }{2}, (n-1))} \cdot \frac{S}{\sqrt{n}}) \le \mu \le \stackrel{-}{x}+({t}_{(1-\frac{\alpha }{2}, (n-1))} \cdot \frac{S}{\sqrt{n}}) ] & = (1-\alpha) \end{align*}\]

\[ IC(\mu)_{(1-\alpha)}= [\stackrel{-}{x} \pm {t}_{c_{(n-1)}} \cdot \frac{S}{\sqrt{n}}] \]

Assim, se \(\stackrel{-}{x}\) é usado como estimativa de \(\mu\) podemos afirmar estar \(100(1-\alpha)\)% confiantes de que o erro não excederá \(({t}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}})\).

 

A quantidade \(\varepsilon=(\stackrel{-}{x}-\mu)= ({t}_{(1-\frac{\alpha }{2}, (n-1))} \cdot \frac{S}{\sqrt{n}})\) é chamada de Erro máximo da estimativa ao se arbitrar um nível de confiança \(\alpha\), (n-1) graus de liberdade e um determinado tamanho amostral.

Exemplo: As vendas de 15 lojas de uma região do país apresentam uma média igual a US$ 20.000,00 e desvio padrão de US$ 8.300,00. Construa o intervalo de confiança para a média ao nível de confiança de 95%.

Dados do problema:

• o tamanho da amostra: \(n=15\);
  
• a média amostral: \(\stackrel{-}{x}=US\$ 20.000\);
  
• o desvio padrão amostral: \(s=US\$ 8.300\);
  
• nível de confiança: \((1-\alpha)=0,95\); e,
• valor extraído da tabela da distribuição de sob \((n-1=15-1=14)\) graus de liberdade \(t_{c}=2,1448\) associado ao nível de confiança estipulado \((1-\alpha)=95\%\).

\[\begin{align*} P[\stackrel{-}{x}-({t}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}}) \le \mu \le \stackrel{-}{x}+({t}_{(1-\frac{\alpha }{2})} \cdot \frac{S}{\sqrt{n}}) ] & = (1-\alpha) \\ P[20000 - ( 2,1448 \cdot \frac{8300}{\sqrt{15}}) \le \mu \le 20000 + ( 2,1448 \cdot \frac{8300}{\sqrt{15}}) ] & = 0,95\\ P[20000 - 4596,41 \le \mu \le 20000 + 4596,41 ] & = 0,95 \end{align*}\]

\[ IC_{(1-\alpha=0,95)} = [US\$ 15403,59 ; US\$ 24496,41] \]

Se quisermos ser rigorosos na interpretação do intervalo de confiança calculado podemos explicar que se extrairmos um grande número de amostras de tamanho 15 dessa população, e para todas elas calcularmos intervalos de confiança como o acima definido, a proporção desses intervalos onde poderemos encontrar a média populacional de vendas será de 0,95 (95 intervalos em 100).

De uma forma mais sintética, podemos afirmar que o intervalo aleatório ]US$ 15.403,59; US$ 24.496,41[, é um intervalo de confiança a 95% para a média de vendas.

De uma forma mais corrente, embora menos correta em termos teóricos, é usual afirmar que, com 95% de confiança a média de vendas se situa entre os valores US$ 15.403,59 e US$ 24.496,41.

Intervalos de confiança unilaterais para uma média amostral sob variância populacional desconhecida e amostras de qualquer tamanho

A Figura 9.18 ilustra um intervalo de confiança unilateral limitado à direita por um valor máximo, de tal sorte que a probabilidade associada ao intervalo de valores da estatística \(T\) inferiores a esse limitante é

\[ P\left [\mu \le \bar{x} + {t}_{c_{(n-1)}} \cdot \frac{S}{\sqrt{n}} \right ] = (1- \alpha) \]

alfa=0.95
prob_desejada1=alfa
df=20
t_desejado1=round(qt(prob_desejada1,df ),4)
d_desejada1=dt(t_desejado1,df)

ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dt,
            args=list(df), 
            fill = "red", 
            xlim = c( t_desejado1, 4),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(0, t_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(-4, 0),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``t'' da distribuição de Student com gl=n-1")  +
  labs(title= "Curva da função densidade \nDistribuição t ", 
       subtitle = "P(-\U221e, t)=(1-\u03b1) em cinza \nP(t, \U221e)= \u03b1 em vermelho ")+
  geom_segment(aes(x = t_desejado1, y = 0, xend = t_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=t_desejado1+0.5, y=d_desejada1, label="t", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=t_desejado1+1, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado1-2.5, y=0.2, label="Intervalo aberto \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+  theme_bw()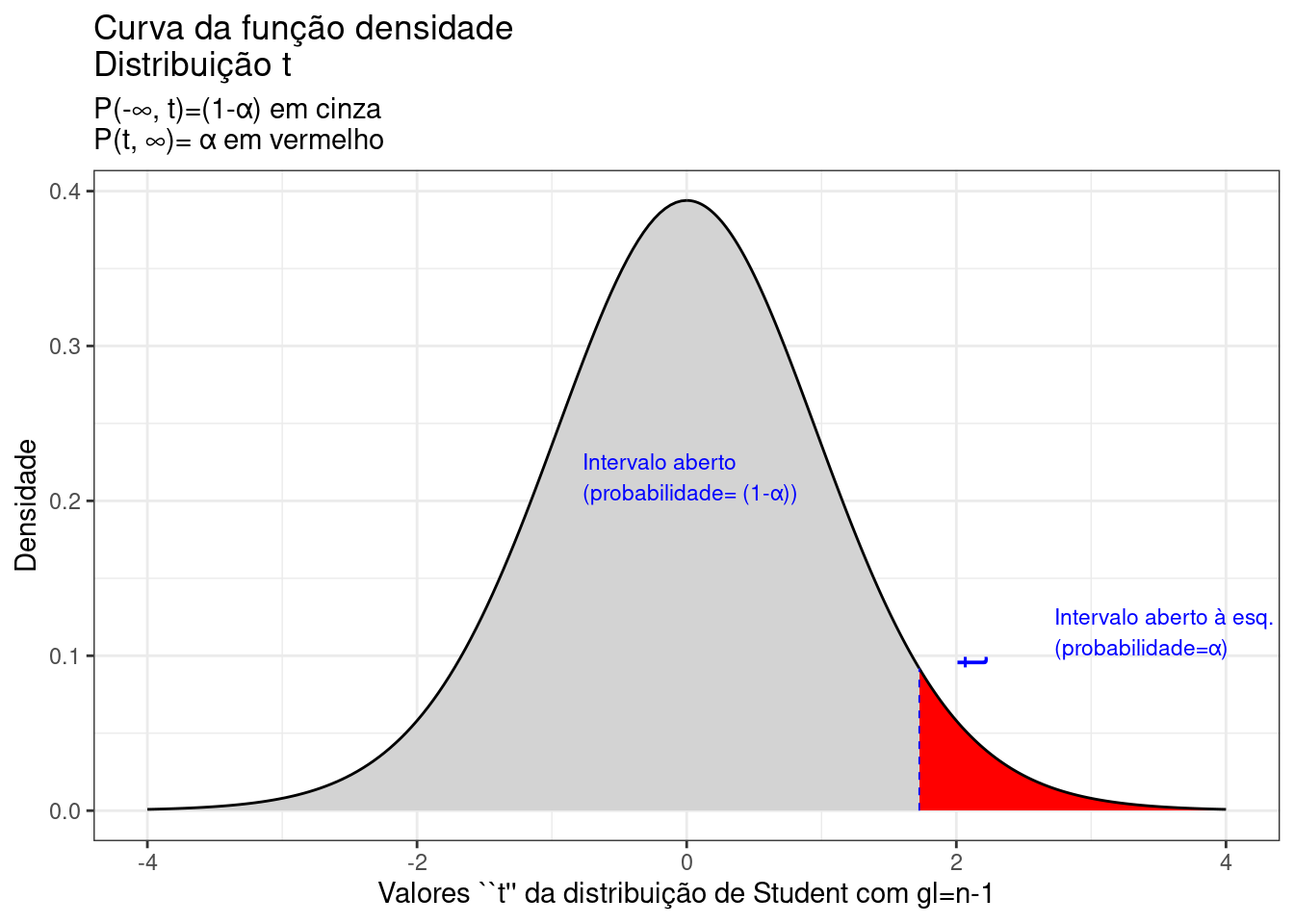

Figure 9.18: Região crítica, além da qual, a probabilidade associada aos valores \(T\) (\((n-1)\) graus de liberdade) é inferior a \(\alpha\), delimitando assim, à esquerda, um intervalo aberto com nível de confiança igual a \((1-\alpha)\)

A Figura 9.19 ilustra um intervalo de confiança unilateral limitado à esquerda por um valor mínimo, de tal sorte que a probabilidade associada ao intervalo de valores da estatística \(T\) superiores a esse limitante é

\[ P\left [\mu \ge \bar{x} - {t}_{c} \cdot \frac{S}{\sqrt{n}} \right ] = (1- \alpha) \]

alfa=0.05
prob_desejada1=alfa
df=20
t_desejado1=round(qt(prob_desejada1,df ),4)
d_desejada1=dt(t_desejado1,df)


ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dt,
            args=list(df), 
            fill = "red", 
            xlim = c(-4, t_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(t_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(0, 4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores ``t'' da distribuição de Student com gl=n-1")  +
  labs(title= "Curva da função densidade \nDistribuição t ", 
       subtitle = "P(-t, \U221e)=(1-\u03b1) em cinza \nP(-\U221e; -t)= \u03b1 em vermelho ")+
  geom_segment(aes(x = t_desejado1, y = 0, xend = t_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=t_desejado1-0.1, y=d_desejada1, label="-t", angle=90, vjust=0, hjust=0, color="blue",size=6)+
  annotate(geom="text", x=t_desejado1-2.5, y=0.1, label="Intervalo aberto à esq. \n(probabilidade=\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado1+1, y=0.2, label="Intervalo aberto \n(probabilidade= (1-\u03b1))", angle=0, vjust=0, hjust=0, color="blue",size=3)+  theme_bw()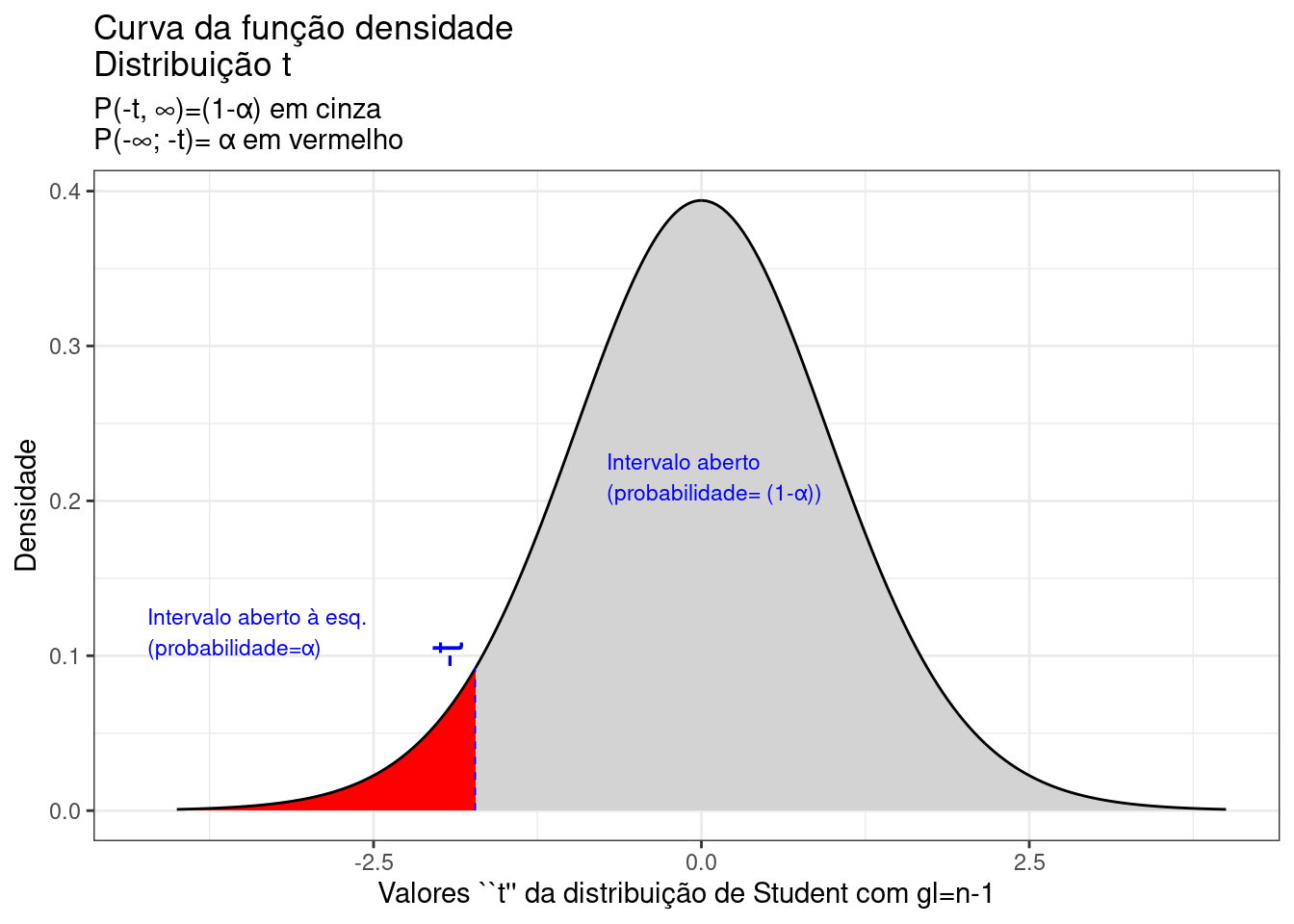

Figure 9.19: Região crítica, aquém da qual, a probabilidade associada aos valores \(T\) (\((n-1)\) graus de liberdade) é inferior a \(\alpha\), delimitando assim, à direita, um intervalo aberto com nível de confiança igual a \((1-\alpha)\)