Capítulo 5 Introdução a variáveis aleatórias

Ao realizar um experimento aleatório frequentemente estamos interessados mais em alguma função do resultado do que no próprio resultado em si:

Ao lançar dois dados, podemos estar interessados na soma “7”, sem nos importar se isso foi decorrente de (1,6),(2,5),(3,4),(4,3),(5,2) ou (6,1).

De forma semelhante, ao lançar três vezes uma moeda, podemos estar interessados no número total de “2 caras” (KK) que ocorre, sem nos preocuparmos se isso decorreu da sequência (K,K,C),(K,C,K) ou (C,K,K).

Da mesma forma, ao planejar uma família de três filhos, podemos estar interessados em ter exatamente 2 filhos do sexo masculino (MM), sem nos importar se isso resultou de (F,M,M), (M,F,M) ou (M,M,F).

Essas quantidades de interesse, ou mais formalmente, essas funções de valor real definidas no espaço amostral (o conjunto de todos os possíveis resultados do experimento), são conhecidas como variáveis aleatórias.

Em outras palavras, uma função \(X\) (geralmente representada por uma letra maiúscula) que associa cada elemento \(\omega\) pertencente ao espaço amostral \(\Omega\) um número real é denominada, de forma mais precisa, como uma variável aleatória ou função estocástica.

\[ X (\Omega) \to \mathcal{R}_{X} \text{, estando } \mathcal{R}_{X}\subseteq \mathcal{R} \]

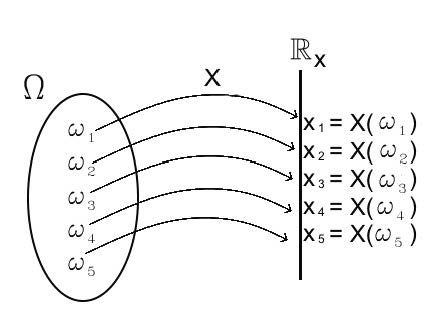
Figure 5.1: Variável aleatória

O domínio dessa função (\(X\)) é o conjunto de todos os possíveis valores numéricos de interesse do experimento aleatório e seu contradomínio está em \(\mathbb{R}\).

Exemplo 1: considere o espaço amostral do experimento aleatório relacionado ao sexo do bebê em três gestações bem sucedidas: \(\Omega=\{\omega_{1}:(FFF), \omega_{2}:(FFM),\omega_{3}:(FMF), \omega_{4}:(MFF),\\ \omega_{5}:(FMM), \omega_{6}:(MFM), \omega_{7}:(MMF), \omega_{8}:(MMM)\}.\) Se estivermos interessados no número de nascimentos do sexo masculino, podemos definir a função \(X\) para associar cada elemento \(\omega_{i}\) em \(\Omega\) a um valor \(x_{i} \in \mathbb{R}\) que apresentará os seguintes resutados: \(X(FFF)=0; X(FFM)=1; X(FMF)=1; X(MFF)=1;\\ X(FMM)=2; X(MFM)=2; X(MMF)=2; X(MMM)=3\) \(\mathcal{R}_{X}=\{x_{1}=0; x_{2}=1; x_{3}=2; x_{4}=3\}\subseteq \mathcal{R}\)

Exemplo 2: considere o espaço amostral do experimento aleatório relacionado à sobrevivência de paciente ao final de 1 dia em uma UTI com quatro leitos: \(\Omega=\{(0,0,0,0),(0,0,0,1),(0,0,1,0),(0,0,1,1),\\ (0,1,0,0),(0,1,0,1),(0,1,1,0),(0,1,1,1),(1,0,0,0),\\ (1,0,0,1),(1,0,1,0),(1,0,1,1),(1,1,0,0),(1,1,0,1),\\ (1,1,1,0),(1,1,1,1)\}.\) Cada elemento do espaço amostral é uma sequência de quatro valores binários \((x_{1},x_{2},x_{3},x_{4})\), onde: \(x_{i}=0\) indica que o paciente no leito \(i\) sobreviveu e \(x_{i}=1\) caso contrário. Se estivermos interessados no número de falecimentos podemos definir a função \(X\) para associar cada elemento \(\omega_{i}\) em \(\Omega\) a um valor \(x_{i} \in \mathbb{R}\) que apresentará os seguintes resultados: \(X(0000)=0; X(0001)=1; X(0010)=1; \dots ; X(1111)=4\) \(\mathcal{R}_{X}=\{x_{1}=0; x_{2}=1; x_{3}=2; x_{4}=3; x_{5}=4\}\subseteq \mathcal{R}\)

Existem dois tipos de variáveis aleatórias: discretas e contínuas:

Os valores possíveis de uma variável aleatória discreta pertencem a um conjunto finito ou infinito enumerável, como \(\{0,1,2, \dots \}\). Exemplos incluem: o número de acidentes em uma semana; o número de partículas αα emitidas por uma fonte radioativa em um intervalo de tempo; ou o número de casos de uma doença em um mês.

Os valores possíveis de uma variável aleatória contínua pertencem a um intervalo contínuo de números reais, como \([a,b]\), \([0,\infty)\) ou \(-\infty, \infty)\). Exemplos incluem: o peso ou a altura de um grupo de pessoas; o tempo de vida de uma lâmpada; o tempo de reação a um estímulo; a concentração de álcool em um certo volume de sangue, a temperatura mínima no inverno Antártico.

A função aletória \(X\) não irá, em geral, simplesmente relacionar os possíveis resultados de interesse do experimento aleatório a números reais. Mas sim computar algumas informações úteis como a probabilidade de sua verificação.