4.5 Dependência e independência de eventos

Pela regra geral da probabilidade de dois eventos eventos condicionados:

\[\begin{align*} P(A|B) & = \frac{ P(A\cap B)}{ P(B)} \\ P(B|A) & = \frac{ P(B\cap A)}{ P(A)} \end{align*}\]

Como a probabilidade de interseção não se altera (\(P(A\cap B)=P(B\cap A)\)), podemos reescrever essas duas expressões:

\[\begin{align*} P(A \cap B) & = P(A|B) \times P(B) \\ P(A\cap B) & = P(B|A) \times P(A) \end{align*}\]

com \(P(B)>0\) e \(P(A)>0\) nas expressões acima.

Se os eventos \(A\) e \(B\) são guardam nenhuma relação de condicionamento eles são chamadas de eventos independentes. Equivale dizer que \(P(A|B)=P(A)\) (ou \(P(B|A)=P(B)\)), a probabilidade de \(A\) não se altera pela prévia ocorrência de \(B\) (ou a de \(B\) pelo de \(A\)).

Portanto, dois eventos são denominados independentes se, e somente se:

\[ P (A \cap B)= P(A) \times P(B) \]

Independência e correlação: se duas variáveis aleatórias são independentes não há associação de natureza alguma entre elas, inclusive a linear, um caso particular de correlação. Todavia uma correlação linear nula não implica em independência posto existirem várias outras formas outras de relacionamento (quadrática, cúbica, ).

Figure 4.17: Independência implica em ausência de qualquer tipo de associação (a recíproca não se aplica

4.5.1 Demonstração clássica de independência

Uma bolsa contém 5 bolas vermelhas e 5 azuis. Nós removemos uma bola aleatória da bolsa, registramos sua cor e a colocamos de volta na sacola. Em seguida, removemos outra bola aleatória da bolsa e registramos sua cor.

• Qual é a probabilidade de a primeira bola ser vermelha ?
  
• Qual é a probabilidade de a segunda bola ser azul?
  
• Qual é a probabilidade de a primeira bola ser vermelha e a segunda bola azul?
  
• A primeira bola retirada foi uma bola vermelha e a segunda bola azul; esses eventos foram independentes ?

Solução:

Probabilidade em se retirar uma bola vermelha em primeiro lugar:

Há 10 bolas das quais 5 são vermelhas . A probabilidade de se retirar uma bola vermelha será:

\[ P(1^{a} vermelha)= \frac{5}{10}= \frac{1}{2} \]

Probabilidade em se retirar uma bola azul em segundo lugar:

O enunciado do experimento assegura que após a retirada da primeira bola ela é devolvida ao sacola; por essa razão, ao se retirar a segunda bola, há novamente 10 bolas no total, das quais 5 são azuis. A probabilidade de se retirar uma bola azul será:

\[ P(2^{a} azul)= \frac{5}{10}= \frac{1}{2} \]

Probabilidade da primeira bola retirada ser vermelha e a segunda ser azul:

Ao se retirar duas bolas do sacola há quatro possíveis combinações de resultados. Nós podemos obter:

1- uma vermelha e depois outra vermelha;
2- uma vermelha e depois uma azul;
3- uma azul e depois uma vermelha; ou,
4- uma azul e depois outra azul;

Queremos saber a probabilidade do segundo resultado após termos obtido uma bola vermelha na primeira seleção.

Como existem 5 bolas vermelhas e 10 bolas no total, existem \(\frac{5}{10}\) possibilidades de obter uma bola vermelha primeiro.

Agora nós colocamos a primeira bola de volta, então há novamente 5 bolas vermelhas e 5 bolas azuis na sacola.

Portanto, há \(\frac{5}{10}\) possibilidades de obter uma segunda bola azul se a primeira bola for vermelha .

Isso significa que existem: \(\frac{5}{10} \times \frac{5}{10}= \frac{25}{100}\) possibilidades de se obter uma bola vermelha em primeiro lugar e uma bola azul em segundo.

Então, a probabilidade associada será de \(\frac{1}{4}\).

A primeira bola retirada foi uma bola vermelha e a segunda bola azul. Esses dois eventos são independentes?

Esses eventos serão independentes se, e somente se:

\[ P (A \cap B)= P(A) \times P(B) \]

\[\begin{align*} P(1^{a} vermelha) & = \frac{5}{10}= \frac{1}{2}\\ P(2^{a} azul) & = \frac{5}{10}= \frac{1}{2}\\ P(1^{a} vermelha,2^{a} azul) & = \frac{25}{100} = \frac{1}{4}\\ \end{align*}\]

Como \(\frac{1}{4}=\frac{1}{2} \times \frac{1}{2}\), os eventos são independentes.

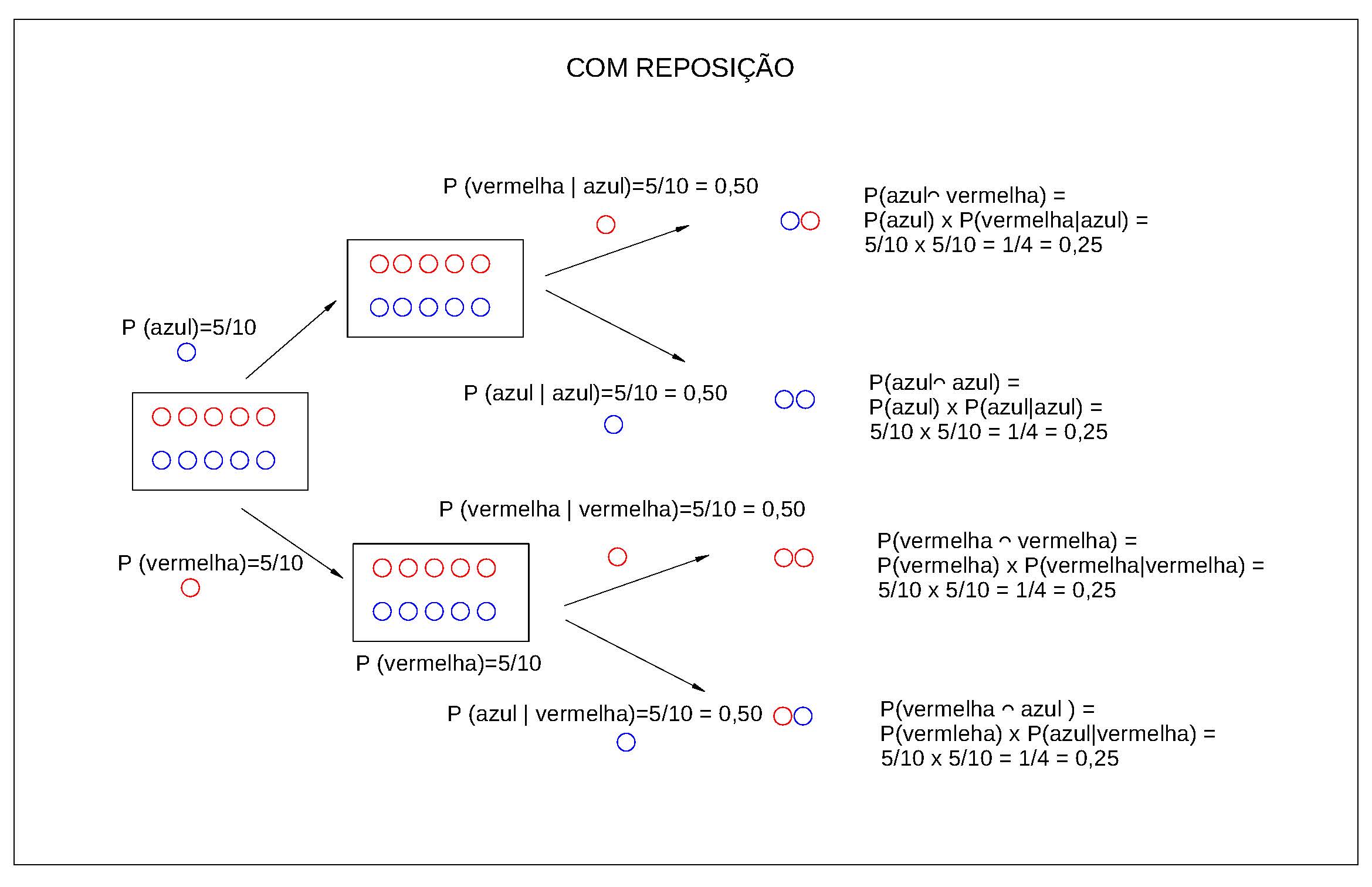
Figure 4.18: Ilustração do experimento aleatório sob a condição de reposição

4.5.2 Demonstração clássica de dependência

E se, ao retirarmos a primeira bola, não a devolvêssemos ao sacola?

Admitamos agora que o enunciado de nosso problema passou a ser:

Uma bolsa contém 5 bolas vermelhas e 5 azuis. Nós removemos uma bola aleatória da bolsa, registramos sua cor e não a colocamos de volta na sacola. Em seguida, removemos outra bola aleatória da bolsa e registramos sua cor.

1- Qual é a probabilidade de a primeira bola ser vermelha ?
2- Qual é a probabilidade de a segunda bola ser azul?
3- Qual é a probabilidade de a primeira bola ser vermelha e a segunda bola azul?
4- A primeira bola retirada foi uma bola vermelha e a segunda bola azul; esses eventos foram independentes ?

Solução:

\(1^{a}\) Etapa: analisar todos os possíveis resultados

Probabilidade da primeira bola retirada ser vermelha e a segunda ser azul:

Ao se retirar duas bolas do sacola há quatro possíveis combinações de resultados. Nós podemos obter:

• uma vermelha e depois outra vermelha;
  
• uma vermelha e depois uma azul;
  
• uma azul e depois uma vermelha ; ou,
  
• uma azul e depois outra azul.

Queremos saber a probabilidade do segundo resultado após termos obtido uma bola vermelha na primeira seleção.

Como existem 5 bolas vermelhas e 10 bolas no total, existem \(\frac{5}{10}\) maneiras de obter uma bola vermelha primeiro.

Entretanto, nessa nova situação, nós não colocamos a primeira bola de volta, então haverá apenas 4 bolas vermelhas e 5 bolas azuis na sacola.

• Haverá \(\frac{4}{9}\) maneiras de obter uma segunda bola vermelha se a primeira bola for vermelha . Isso significa que existem: \(\frac{5}{10} \times \frac{4}{9}= \frac{20}{90}\) maneiras de se obter uma bola vermelha em primeiro lugar e uma bola vermelha em segundo. Então, a probabilidade associada será de \(\frac{2}{9}\);

• Haverá \(\frac{5}{9}\) maneiras de obter uma segunda bola azul se a primeira bola for vermelha . Isso significa que existem: \(\frac{5}{10} \times \frac{5}{9}= \frac{25}{90}\) maneiras de se obter uma bola vermelha em primeiro lugar e uma bola azul em segundo. Então, a probabilidade associada será de \(\frac{5}{18}\);

• Haverá \(\frac{5}{9}\) maneiras de obter uma segunda bola vermelha se a primeira bola for azul. Isso significa que existem: \(\frac{5}{10} \times \frac{5}{9}= \frac{25}{90}\) maneiras de se obter uma bola azul em primeiro lugar e uma bola vermelha em segundo. Então, a probabilidade associada será de \(\frac{5}{18}\).

• Haverá \(\frac{4}{9}\) maneiras de obter uma segunda bola azul se a primeira bola for azul. Isso significa que existem: \(\frac{5}{10} \times \frac{4}{9}= \frac{20}{90}\) maneiras de se obter uma bola azul em primeiro lugar e uma bola azul em segundo. Então, a probabilidade associada será de \(\frac{2}{9}\);

Resumo das probabilidades calculadas:

1 -uma vermelha e depois outra vermelha : \(\frac{2}{9}\);
2- uma vermelha e depois uma azul: \(\frac{5}{18}\);
3- uma azul e depois uma vermelha : \(\frac{5}{18}\); e,
4- uma azul e depois outra azul: \(\frac{2}{9}\).

\(2^{a}\) Etapa: analisar a possibilidade de se obter uma bola vermelha na primeira extração:

• uma vermelha e depois outra vermelha : \(\frac{2}{9}\);
  
• uma vermelha e depois uma azul: \(\frac{5}{18}\).

A probabilidade total de se obter uma bola vermelha na primeira extração será:

\[ P(1^{a} vermelha)= \frac{2}{9} + \frac{5}{18} = \frac{1}{2} \]

\(3^{a}\) Etapa: analisar a possibilidade de se obter uma bola azul na segunda extração:

• uma vermelha e depois uma azul: \(\frac{5}{18}\);
  
• uma azul e depois outra azul: \(\frac{2}{9}\).

A probabilidade total de se obter uma bola azul na segunda extração será:

\(P(2^{a} azul)= \frac{5}{18} + \frac{2}{9} = \frac{1}{2}\)

\(4^{a}\) Etapa: analisar a possibilidade de se obter uma bola vermelha e em seguida azul:

• uma vermelha e depois outra azul: \(\frac{5}{18}\);

\(5^{a}\) Etapa: Esses dois eventos são independentes?

Esses eventos serão independentes se, e somente se:

\[ P (A \cap B)= P(A) \times P(B) \]

\[\begin{align*} P(1^{a} vermelha) & = \frac{2}{9} + \frac{5}{18} = \frac{1}{2} \\ P(2^{a} azul) & = \frac{5}{18} + \frac{2}{9} = \frac{1}{2} \\ P(1^{a} vermelha,2^{a} azul) & = \frac{5}{18} \\ \end{align*}\]

Como \(\frac{5}{18} \neq \frac{1}{2} \times \frac{1}{2}\), os eventos não são independentes.

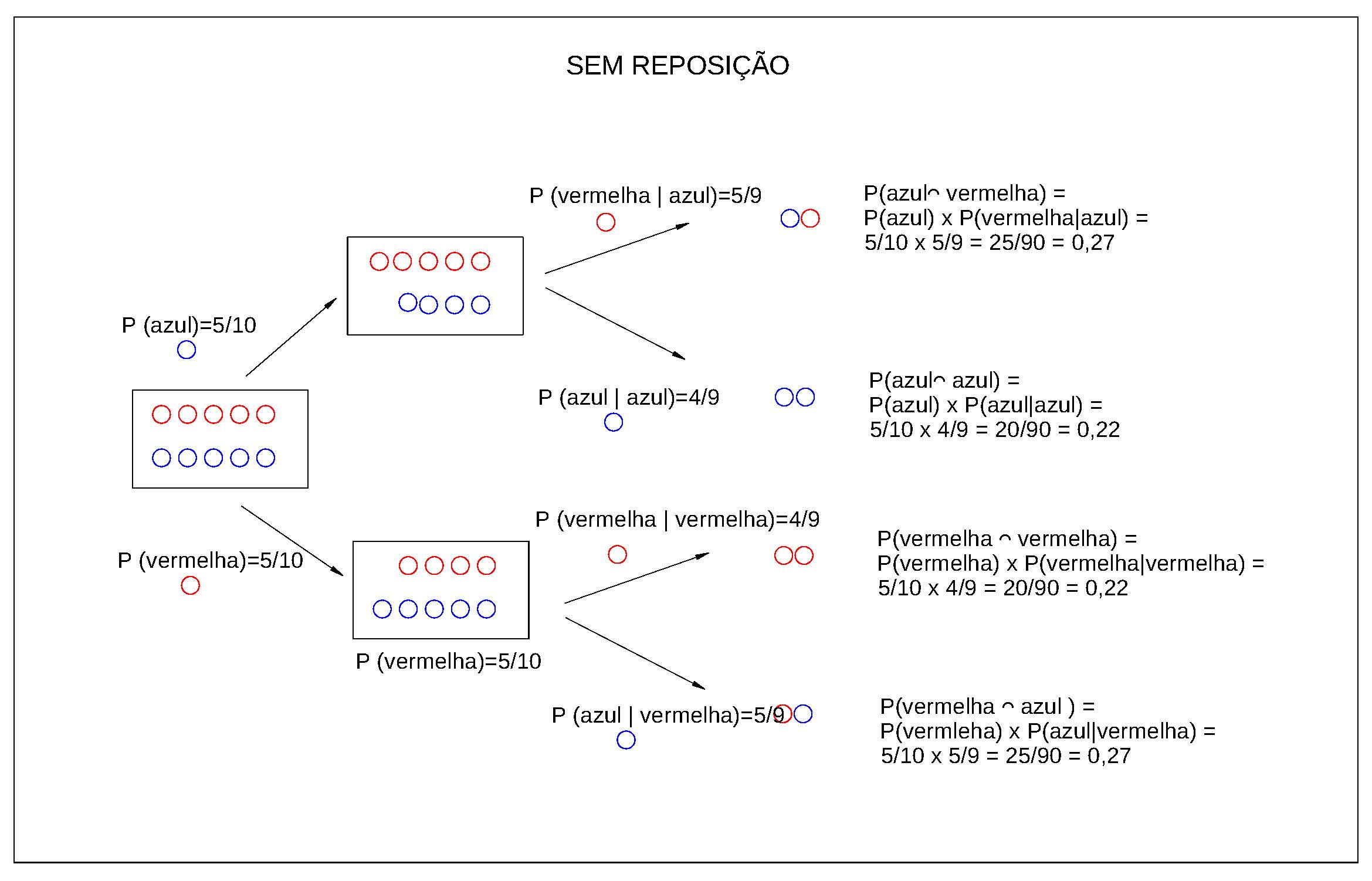
Figure 4.19: Ilustração do experimento aleatório sob a condição de não reposição