7.10 Amostragem probabilística

Uma amostragem de natureza probabilística é aquela que reúne todas as técnicas pelas quais se deixa completamente ao acaso a escolha dos elementos da população a serem incluídos na amostra. A aleatorização visa assegurar que a informação extraída da amostra possa ser generalizada na população de origem. A cada extração a probabilidade de um elemento ser incluído é igual para todos (embora ela e altere em razão de ser uma extração sem reposição).

7.10.1 Amostragem aleatória simples (AAS)

Consiste na seleção de $n$ elementos amostrais de tal modo que cada um deles tenha a mesma probabilidade de pertencer à amostra que os demais.

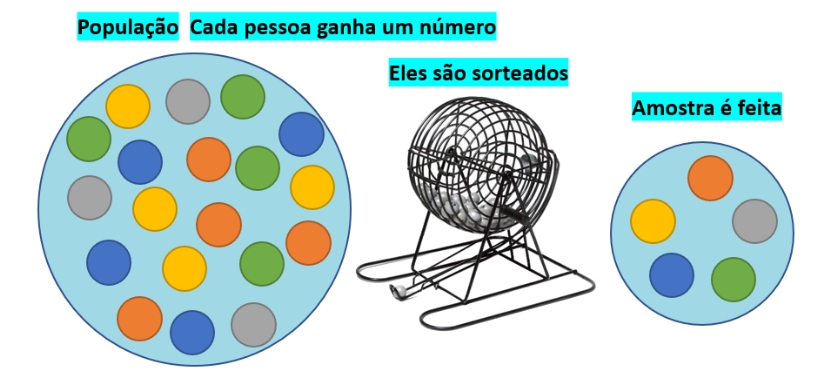
Figure 7.3: Amostra aleatória simples AAS

Duas situações distintas:

com reposição do elemento amostral escolhido: o mesmo elemento da população pode ser amostrado mais de uma vez (a probabilidade de seleção não se altera); ou,
sem reposição: cada elemento da população é amostrado uma única vez (a probabilidade de seleção se altera)

Amostragem aleatória simples sem reposição. Admita uma população ($N=5$) composta pelos elementos: {a, b, c, d, e} (podem ser as rendas anuais de cinco pessoas, os pesos de cinco vacas ou cinco modelos diferentes de aviões) da qual se deseje extrair uma amostra de tamanho $n=3$.

Haverá 10 amostras possíveis de serem extraídas com tamanho 3 ($n=3$): {abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde} pois:

\[ C_{(N,n)} = \frac{ N! }{ n! \times ( N-n)!}=10 \]

Amostragem aleatória simples com reposição. Considere agora a mesma população anterior ($N=5$) e o mesmo tamanho da amostra ($n=3$). Se a amostragem for feita com reposição teremos então $N^{n}=125$ amostras possíveis de serem extraídas: {aaa, aab, aac, aad, aae, aba, abb, abc, abd, abe, ……}

# Dados
conjunto=c("a", "b", "c", "d", "e")


# As 10 combinações possíveis tomando-se 3 elementos:
library(combinat)

## 
## Attaching package: 'combinat'

## The following object is masked from 'package:utils':
## 
##     combn

#combn(conjunto, 3) (remova o # para executar)

# As 125 permutações possíveis tomando-se 3 elementos:
# permn(conjunto) (remova o # para executar)

# Extração de uma amostra (sem reposição) composta por 3 elementos do conjunto:
amostra_sr=sample(conjunto, 3, replace=FALSE)
amostra_sr

## [1] "c" "e" "b"

# Extração de uma amostra (com reposição) composta por 3 elementos do conjunto:
amostra_cr=sample(conjunto, 3, replace=TRUE)
amostra_cr

## [1] "e" "c" "c"

Do ponto de vista da quantidade de informação contida na amostra, a amostragem sem reposição é mais adequada.

Todavia a amostragem com reposição conduz a um tratamento teórico mais simples, pois ele implica que tenhamos independência entre as unidades selecionadas (não há alteração na probabilidade de seleção).

Para populações muito grandes a reposição ou não é irrelevante.

Uma vez determinadas as possíveis amostras, segue-se o problema de como elas serão efetivamente extraídas na prática numa amostragem aleatória simples.

Numa situação simples como a que acabamos de conceber poderíamos escrever cada uma das 10 (ou 125) possíveis amostras em um pedaço de papel e colocá-los em uma urna para serem sorteados.

Ou então enumerar os elementos da lista de possibilidades atribuindo um número a cada um e, em seguida, usar uma tabela de números aleatórios (ou um programa computacional para sua geração) para a escolha dos elementos que integrarão a amostra.

Uma AAS raramente é realizada na prática pois é necessário dispor de uma listagem bem definida a priori.

Assim, sob circunstâncias reais, um planejamento amostral pode ser definido de modo a assegurar que uma amostra mais informativa, mais barata e rápida possa ser extraída, principalmente quando a amostragem aleatória simples mostrar-se impraticável.

Em estudos de larga escala muitas vezes requerem uma abordagem mista.

A amostragem mista tem vantagens a nível prático, quando se conhecem algumas informações da população; assim sendo define-se uma característica dos elementos a incluir na amostra, deixando-se os restantes fatores ao acaso.

Neste tipo de amostragem salientam-se os seguintes métodos:

1- sistemática;
2- estratificada; e,
3- por conglomerado.

7.10.2 Amostragem aleatória sistemática

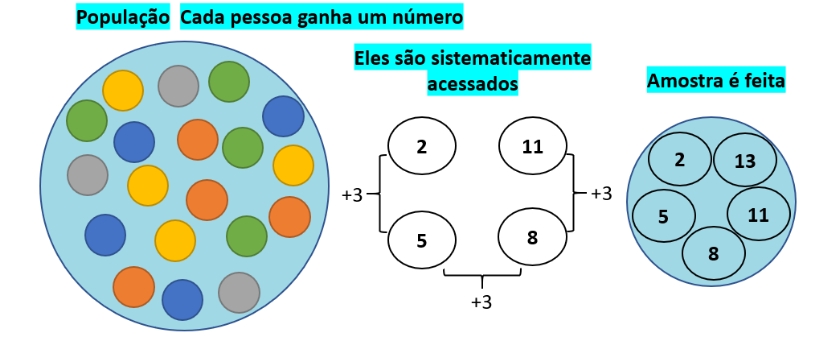
Figure 7.4: Amostra sistemática

Quando os elementos da população estão dispostos sob alguma maneira organizada e aleatória (linha de produção, listagens, … ) a extração de elementos pode ser realizada pela estipulação de um ponto de partida aleatório (o primeiro elemento a ser tomado como integrante da amostra) e de um passo (intervalo), de modo que a seleção dos demais elementos será feita a cada $k$ elementos da listagem.

Roteiro:

se $N$ é o tamanho da população a ser amostrada;
e $n$ o tamanho da amostra que se deseja;

calcula-se o passo (intervalo) a ser adotado para a extração dos demais elementos amostrais. O primeiro elemento a ser coletado será aleatoriamente escolhido dentre os $k$ primeiros.

\[ S=\frac{N}{n} \]

Sorteia-se o ponto de partida (um dos $S$ números do primeiro intervalo) e depois, a cada $S$ elementos da população, retira-se um para fazer parte da amostra, até completar o valor de$n$.

Algumas situações possíveis de se encontrar:

se $S$ for fracionário pode-se aumentar $n$ até tornar $S$ um inteiro;
reduzir $N$ em 1 unidade;
se $N$ for um número primo, excluem-se por sorteio alguns elementos da população para tornar $S$ inteiro.

Exemplo: considerem uma população composta por pelos seguintes elementos P={1, 2, 3, 4, 5, 6, 7, 8, 9, 10} (N=10) da qual desejamos extrair uma amostra de tamanho 3 (n=3).

O passo $S$ (o intervalo de extração de cada elemento) será igual a $S=\frac{N}{n}=\frac{10}{3}=3,33$ (fracionário). Aumentando-se para $n=4$ resultará também em um $S$ fracionário (2,5). Com $n$=5, $S=2$. O primeiro elemento a integrar a amostra será será aleatoriamente escolhido dentre os 5 ($S$) primeiros. Assim, as duas possíveis amostras serão:

\[\begin{align*} A1 & = {1, 3, 5, 7, 9}; e, \\ A2 & = {2, 4, 6, 8, 10}. \\ \end{align*}\]

Avaliar, alternativamente, excluir aleatoriamente 1 elemento da população ($N=9$). Mantendo-se $n=3$ teremos $S=3$.

\[\begin{align*} A1 & = {1, 4, 7}; \\ A2 & = {2, 5, 8}; e, \\ A3 & = {3, 7, 9}. \\ \end{align*}\]

Exemplo: uma operadora telefônica pretende saber a opinião de seus assinantes comerciais sobre seus serviços na cidade de Florianópolis. Supondo que há 25.037 assinantes comerciais e a amostra precisa ter no mínimo 800 elementos, mostre como seria organizada uma amostragem sistemática para selecionar os respondentes sabendo que a operadora dispõe de uma lista ordenada alfabeticamente com todos os seus assinantes.

Calculando o passo ($S$):

\[\begin{align*} S & = \frac{N}{n} \\ & = \frac{25037}{800} \\ & = 31,29 \end{align*}\]

Aumentar $n$ não irá resolver o problema ($N=25037$ é um número primo). Arredondar $S$ para cima irá extrapolar o tamanho da população ($32 \times 800=25600 >25037$).

Podemos arredondar $S$ para baixo ($31 \times 800=24800$) para baixo e excluir aleatoriamente 237 elementos da população (é uma população relativamente grande e isso não acarretará problema algum).

Assim nossa amostra será composta por 800 elementos ($n$) de uma população de (reduzida a) $24800$ elementos. Sorteamos aleatoriamente o primeiro elemento dentre os 31 primeiros da listagem. Os demais, a cada 31 elementos.

Na amostragem sistemática deve-se avaliar o risco de periodicidades sistemáticas:

se lista de elementos estiver organizada com base em alguma informação da população (escolaridade, renda, …) que possa induzir a algum tipo de viés;
se em um processo produtivo for sabidamente reconhecido que falhas podem se tornar mais frequentes a cada certo número de unidades produzidas (máquinas descalibradas).

7.10.3 Amostragem aleatória estratificada

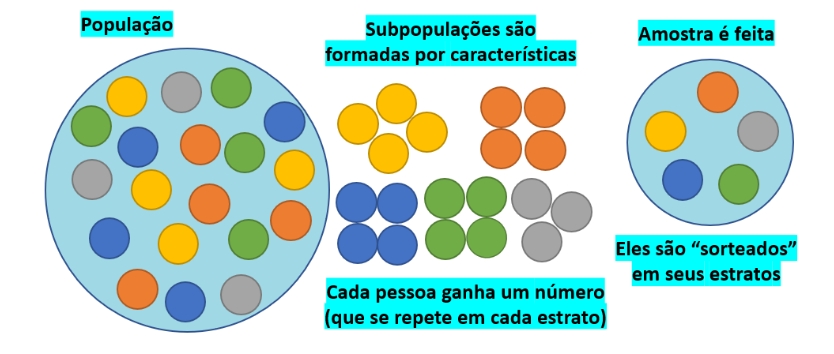
Figure 7.5: Amostra estratifiada

Quando se pode identificar na população a presença de grupos distintos (estratos) a amostragem estratificada se dá pela realização de amostragens aleatórias simples dentre os elementos de cada um desses grupos.

Um estrato é uma subdivisão da população onde se observa a existência de uma razoável homogeneidade interna da informação desejada. Desse modo, é esencial para que a amostra final tenha qualidade, que entre os estratos estabelecidos exista heterogeneidade e assim, cada indivíduo pertença a apenas um estrato.

Há dois modos possíveis de se realizar uma amostragem estratificada:

não proporcional; e,
proporcional.

Em uma amostragem estratificada não proporcional o total de elementos extraídos de cada estrato é igual à razão do tamanho da amostra pelo número de estratos (de cada estrato serão escolhidos aleatoriamente um mesmo número de elementos).

Esse modo de extração de elementos implica considerar igual representatividade de cada estrato na população, independentemente de quantos elementos ele abrigue (estratos menores teriam um mesmo peso que estrato maiores).

Já na amostragem estratificada proporcional a amostra extraída de cada um dos estratos segue algum critério de ponderação do peso ou variabilidade de cada estrato da população.

Na alocação proporcional ao tamanho dos estratos a proporção relativa de cada uma das $k$ amostras extraídas ($n_{k}$) em relação ao tamanho de cada um dos $k$ extratos ($N_{k}$) é a mesma (garantindo que estratos maiores tenham mais elementos dentro da amostra final e que estratos menores tenham menos presença nela):

\[ \frac{n_{1}}{N_{1}} = \frac{n_{2}}{N_{2}} = \dots = \frac{n_{k}}{N_{k}} \]

Onde:

$N$ é o tamanho da população;
$n$ o tamanho da amostra que se deseja extrair da população;
$N_{i}$ é o tamanho do $i-ésim$o estrato da população, tal que $N=N_{1}+N_{2}+\dots+N_{k}$;
$n_{i}$ o tamanho da $i-ésima$ amostra a ser extraída do $i-ésimo$ estrato, tal que $n = n_{1} + n_{2} + \dots + n_{k}$.

O tamanho da $i-ésima$ amostra a ser extraída de um $i-ésimo$ estrato será determinada em razão do tamanho da amostra que se deseja extrair ($n$), o tamanho da população ($N$) e o tamanho do $i-ésimo$ estrato ($N_{i}$) tal que:

\[ n_{i} = \frac{N_{i}}{N} \cdot n \]

para i=1,2,…,k estratos.

Exemplo: considerem uma comunidade universitária composta 8000 indivíduos (N=8000) sendo 800 professores ($N_{1}=800$), 1200 funcionários ($N_{2}=1200$) e 6000 estudantes ($N_{3}=6000$), da qual se estipulou extrair uma amostra de tamanho igual a 900 elementos ($n=900$) para fins de uma pesquisa sobre o estilo de liderança preferido, que se considera ser diferente para cada grupo componente da comunidade acadêmica.

Numa amostragem estratificada não proporcional os elementos são extraídos em igual quantidade de cada um dos estratos:

300 professores;
300 funcionários; e,
300 alunos.

Numa amostragem estratificada uniforme todas os elementos são extraídos em quantidade de modo independente do peso proporcional dos estratos na população. Esse tipo de amostragem apresenta resultados menos precisos mas, em contrapartida, estudar características de cada camada de forma mais eficiente.

Numa amostragem estratificada proporcional os elementos são extraídos de cada um dos estratos considerando-se seus diferentes tamanhos (suas proporções em relação à população total):

o estrato dos professores possui $N_{p}=800$ elementos;
o estrato dos funcionários possui $N_{f}=1200$ elementos; e,
o estrato dos estudantes possui $N_{e}=6000$ elementos.

Para uma amostra com um total de $n=900$ elementos seguem-se as quantidades a serem extraídas aleatoriamente de cada u dos três estratos:

$n_{p}=\frac{N_{p}}{N}.n=\frac{800}{8000}.900=90$ professores;
$n_{f}=\frac{N_{f}}{N}.n=\frac{1200}{8000}.900=135$ funcionários;
$n_{e}=\frac{N_{e}}{N}.n=\frac{6000}{8000}.900=675$ alunos;

Partindo-se desses tamanhos amostrais determinados (90 professores, 135 funcionários e 675 alunos) pode-se recorrer à extração sistemática usando-se a listagem dessas três categorias:

$S_{p}=\frac{N_{p}}{n_{p}}$ em que $S_{p}$ é o passo a ser seguido na extração de $n_{p}$ professores (90) da ``população’’ de $N_{p}$ professores (800);
$S_{f}=\frac{N_{f}}{n_{f}}$ em que $S_{f}$ é o passo a ser seguido na extração de $n_{f}$ funcionários (135) da ``população’’ de $N_{f}$ funcionários (1200); e,
$S_{e}=\frac{N_{e}}{n_{e}}$ em que $S_{e}$ é o passo a ser seguido na extração de $n_{e}$ alunos (675) da ``população’’ de $N_{e}$ alunos (6000).

Muitos ajustes devem ser feitos pois, de modo frequente, os resultados dos passos obtids na prática resultam em números fracionários. Todavia, devemos ter sempre procurar não reduzir o tamanho amostral e ter em mente que o tamanho da população não pode ser aumentado.

Para os professores: $S_{p}=\frac{800}{90}=8,88$. Se tomamos $S_{p}=9$ (um professor a cada nove da lista) veremos que para extrair 90 professores a população teria de ser de 810 (a população é de 800). Uma das opções seria usar $S_{p}=8$ e se extrair 100 professores (uma amostra um pouco maior). Outra possibilidade seria ainda usar $S_{p}=8$ remover aleatoriamente 80 professores da população e então tomar 90 professores (pois com $S_{p}=8$, $8 . 90=720$).

Para os funcionários: $S_{f}=\frac{1200}{135}=8,88$ (o mesmo porque essas amostras foram estabelecidas de modo proporcional). Se tomamos $S_{f}=9$ (um funcionário a cada nove da lista) veremos que para extrair 135 funcionários a população teria de ser de 1215 (a população é de 1200). Uma das opções seria usar $S_{f}=8$ e se extrair 150 funcionários (uma amostra um pouco maior). Outra possibilidade seria ainda usar $S_{f}=8$ remover aleatoriamente 120 funcionários da população e então tomar 135 funcionários (pois com $S_{f}=8$, $8 . 135=1080$).

Do mesmo modo para os alunos: $S_{e}=\frac{6000}{675}=8,88$ (o mesmo porque essas amostras foram estabelecidas de modo proporcional). Se tomamos $S_{e}=9$ (um aluno a cada nove da lista) veremos que para extrair 675 alunos a população teria de ser de 6075 (a população é de 6000). Uma das opções seria usar $S_{e}=8$ e se extrair 750 alunos (uma amostra um pouco maior). Outra possibilidade seria ainda usar $S_{e}=8$ remover aleatoriamente 600 funcionários da população e então tomar 600 alunos (pois com $S_{e}=8$, $8 . 135=1080$).

Ao final poderíamos extrair então 100 professores, 150 funcionários e 750 alunos; ou, pela segnda possibilidade, extrair 90 professores, 135 funcionários e 600 alunos (eliminando-se aleatoriamente elementos das populações antes de se sistematizar a extração, como antes explicado).

A proporção de elementos extraídos de cada um dos estratos é constante entre os extratos, asseguando uma extração proporcional:

\[ \frac{100}{800} = \frac{150}{1200} =\frac{750}{6000}=0,125 \\ \frac{90}{720} = \frac{135}{1080} =\frac{675}{5400}=0,125 \]

Pode-se otimizar uma amostragem estratificada proporcional consideran-de também sua variabilidade interna. O tamanho de cada uma das amostras ($n_{1},n_{2},\dots,n_{k}$) dos diferentes estratos são proporcionais aos tamanhos dos estratos ($N_{1},N_{2},\dots, N_{k}$) e também segundo algum critério adicional (otimização), como a variabilidade interna de cada estrato ($\sigma_{1},\sigma_{2},\dots,\sigma_{k}$) de modo a se manter iguais as razões:

\[ \frac{n_{1}}{N_{1} \cdot \sigma_{1}} = \frac{n_{2}}{N_{2} \cdot \sigma_{2}} = \dots = \frac{n_{k}}{N_{k} \cdot \sigma_{k}} \]

Onde:

$N$ é o tamanho da população;
$n$ o tamanho da amostra que se deseja extrair da população;
$N_{i}$ é o tamanho do $i-ésim$o estrato da população, tal que $N=N_{1}+N_{2}+\dots+N_{k}$;
$n_{i}$ o tamanho da $i-ésima$ amostra a ser extraída do $i-ésimo$ estrato, tal que $n = n_{1} + n_{2} + \dots + n_{k}$;e,
$\sigma_{i}$ é o desvio padrão do $i-ésimo$ estrato.

O tamanho da $i-ésima$ amostra a ser extraída de um $i-ésimo$ estrato será determinada em razão do tamanho da amostra que se deseja extrair ($n$), o tamanho da população ($N$), do tamanho e variabilidade do $i-ésimo$ estrato ($N_{i}$ e $\sigma_{i}$) tal que:

\[ n_{i} =\frac{ n \cdot N_{i} \cdot \sigma_{i} }{ N_{1} \cdot \sigma_{1} + N_{1} \cdot \sigma_{1} + \dots+ N_{k} \cdot \sigma_{k}} \]

para i=1,2,…, k estratos.

Exemplo: considere estudar a opinião de estudantes de uma universidade com relação à legalização do aborto. A equipe possui dados descritivos relacionados ao sexo, orientação religiosa e rendimento médio familiar de toda a comunidade acadêmica. Na revisão bibliográfica identifica-se que algumas das variáveis que habitualmente implicam em opiniões diferentes (escolaridade e idade) já não mais precisam ser consideradas; todavia, outras ainda devem ser consideradas. Assim, um plano de estratificação de vários niveis pode ser estabelecido partindo-se da premissa de homogeneidade de opinião interna em cada um deles: sexo, orientação religiosa e rendimento familiar.

Considerando uma amostra de $n=1.000$ estudantes e as seguintes medidas descritivas disponibilizadas pela universidade e relacionadas à sua população de estudantes:

sexo: 35% masculino e 65% feminino;
orientação religiosa: 60% católica; 20% evangélica; 10% sem; 5% espírita e 5% outras; e,
rendimento médio mensal familiar: 35% até R$ 4.000,00, 65% acima de R$ 4.000,00.

podemos estabelecer vária camadas estratificadas proporcionalmente, tal como a ilustrado na Figura 7.6.

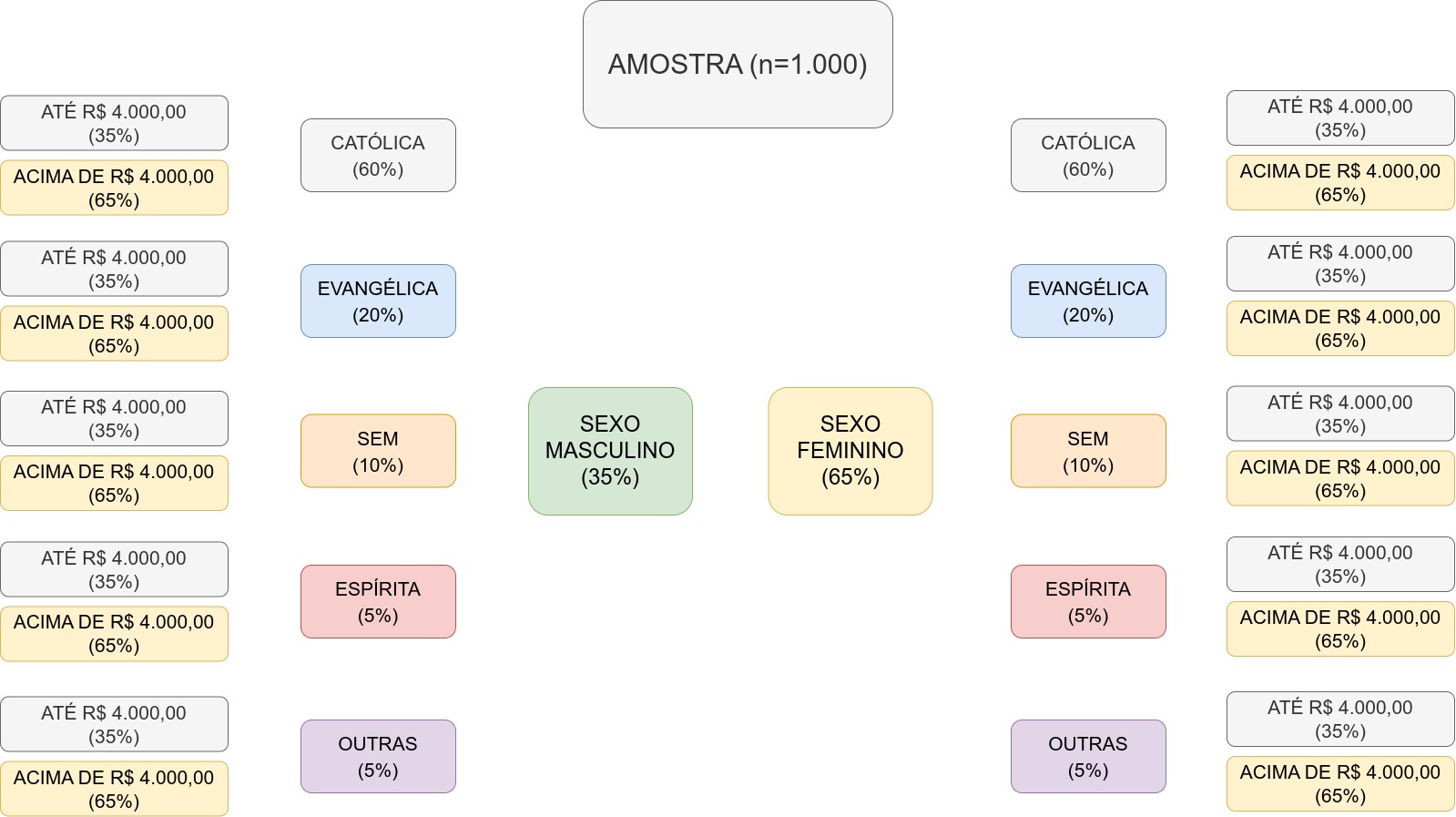
Figure 7.6: Plano de estratificação proporcional

7.10.4 Amostragem aleatória por conglomerados

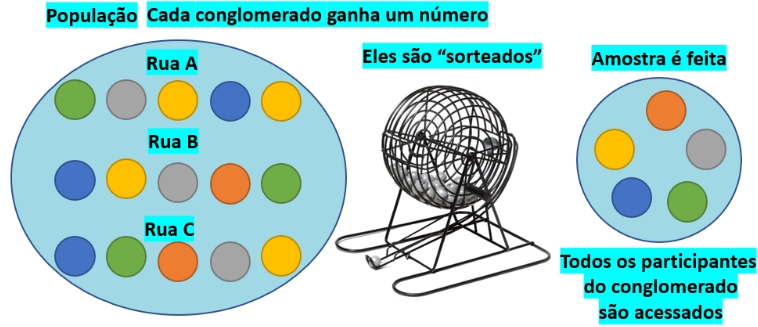
Figure 7.7: Amostragem por conglomerados

Muitas vezes a dispersão espacialde uma população a ser investigada torna impeditiva uma amostragem aleatória simples.

Um modo de contornar essa dificuldade é dividir a área total onde se assenta a população de interesse em várias áreas geográficas menores e sem sobreposição, tais como cidades, regionais de cidades, bairros, quarteirões de um bairro, …. Essa subdivisão pode também ser realizada valendo-se de critérios organizacionais como, por exempo, universidades, escolas, grau escolar, departamentos de uma empresa, ….

As subpopulações que se localizam nessas áreas menores passam a ser denominadas de conglomerados e são como que representações em escala reduzida da população total.

A heterogeneidade presente na população original passa a estar representada dentro de um conglomerado. Ou seja, é essencial para a qualidade final da amostra extraída desse modo, que os elementos dentro de cada conglomerado sejam tão diversos quanto a diversidade que se observa nos elementos da população total (a ideia de representação em escala reduzida).

Em uma amostragem de apenas 1 estágio, após serem aletariamente sorteados um certo número de conglomerados, todos os elementos internos desses conglomerados são estudados.

Todavia, considerando que os elementos de um conglomerado natural dentro de uma população são habitualmente mais homogêneos do que os elementos da população total (os moradores de um bairro são mais semelhantes entre si do que todos os moradores do município), pode não ser necessário um grande número de elementos para se representar adequadamente um conglomerado natural.

Uma diretriz científica num processo de amostragem por conglomerados é maximizar o número de conglomerados e diminuir o número de elementos aleatoriamente escolhidos dentro de cada um deles.

Recomenda-se observar as diferenças de tamanho existentes entre cada conglomerado, de modo a equilibrar a probabilidade. A probabilidade de seleção de um elemento num desenho de amostragem com probabilidade proporcional ao tamanho:

na primeira etapa é dada a cada conglomerado uma oportunidade de seleção proporcional ao seu tamanho; e,
na segunda etapa um mesmo número de elementos é escolhido dentro de cada conglomerado selecionado.

Esses procedimentos igualam as probabilidades últimas de seleção de todos os elementos da população pois:

conglomerados com mais elementos têm maior probabilidade de serem selecionados; e,
elementos em conglomerados maiores têm menor chance de seleção do que elementos em conglomerados menores.

Exemplo: a população universitária de Londrina (estimada em 25.000 estudantes) pode ser entendida como distribuída em vários conglomerados organizacionais como, por exemplo: UEL; UNIFIL; PUC; INESUL; UTFPr; Arthur Thomas; CESUMAR; Pitágoras; Positivo; ….

Se desejamos realizar uma pesquisa entre os estudantes universitários de Londrina (na qual sabe-se que não fará diferença se a instituição é pública ou privada) podemos sortear aleatoriamente alguns desses conglomerados.

Entretanto, lembrando que todos os elementos de um conglomerado devem ser entrevistados, pode ser que o número de estudantes em cada conglomerado escolhido ainda seja por demais elevado.

Nesse caso, um segundo estágio (como, por exemplo, utilizar a subdivisão administrativa que as universidades habitualmente adotam ao se subdividir em diversos centrso de estudos como conglomerados dentro dela) pode ser proposto.

Assim como na estratificação, a proposição de conglomerados deve sempre consider as variáveis condicionantes relacionadas com o objeto de estudo para que as informações de todas as unidade amostrais finais a serem entrevistadas possa ser usada seguramente para se inferir sobre a informação na população sob estudo.

Exemplo: a Pesquisa Nacional por Amostra de Domicílios (PNAD) do IBGE coleta informações demográficas e socioeconômicas sobre a população brasileira. Sinteticamente, utiliza amostragem por conglomerados em três estágios:

primeiro estágio: amostras de municípios (conglomerados) para cada uma das regiões geográficas do Brasil (Norte, Nordeste, Centro-Oeste, Sudeste e Sul);
segundo estágio: setores censitários sorteados (subdivisão estabelecida pelo IBGE dentro de um município) em cada município (conglomerado sorteado);
terceiro estágio: domicílios sorteados aleatoriamente em cada setor censitário.

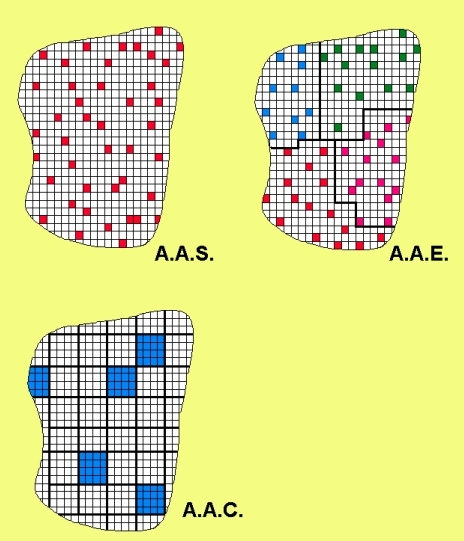
Figure 7.8: Ilustração comparativa dos principais modos de extração de amostras

Exemplo: considere estudar a opinião de estudantes universitários de toda uma cidade com relação à legalização do aborto. A equipe possui dados descritivos relacionados ao sexo, orientação religiosa e rendimento médio familiar de toda a comunidade acadêmica. Na revisão bibliográfica identifica-se que algumas das variáveis que habitualmente implicam em opiniões diferentes (escolaridade e idade) já não mais precisam ser consideradas; todavia, outras ainda devem ser consideradas. Assim, um plano de estratificação de vários niveis pode ser estabelecido partindo-se da premissa de homogeneidade de opinião interna em cada um deles: sexo, orientação religiosa e rendimento familiar.

Nesse caso, podemos considerar cada universidade como um conglomerado. Numa primeira etapa promovemos um sorteio e, na sequência, uma estratitificação da amostra total em termos da população estudantil de cada conglomearado. A partir desse ponto, em cada universidade, estratificações suplementares são feitas para se considerar proporcionalmente as diferentes opiniões (sexo, orientação religiosa, renda).

Ao final, após vários estágios, uma amostra não probabilística pode ser extraída de cada grupo individualizado anteriormente, tal como a ilustrado na Figura 7.9.

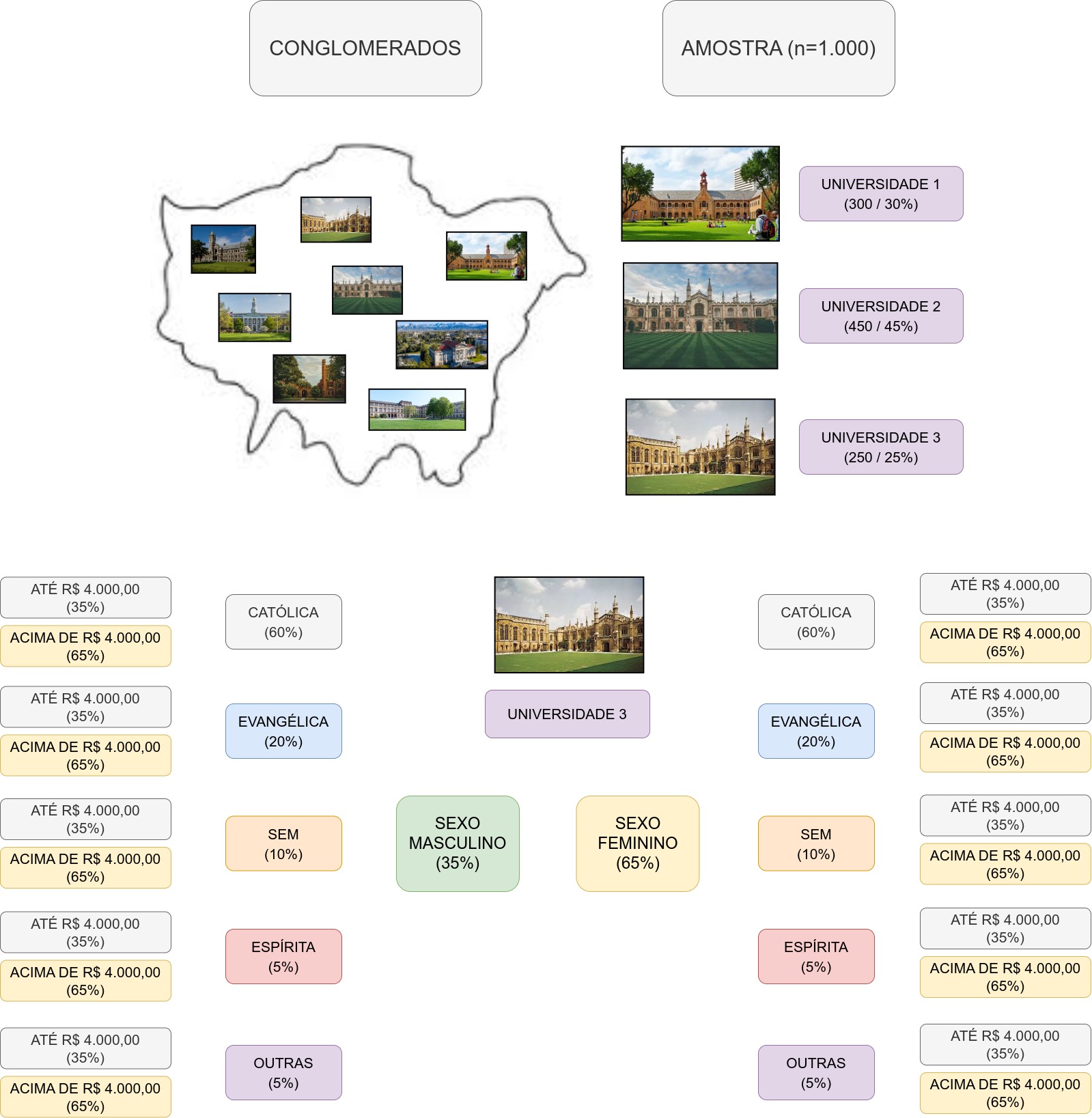
Figure 7.9: Planejamento da extração da amostra