3.6 Diferentes posições da média, moda e mediana (2\(^{o}\) quartil)
Essas três medidas podem se apresentar com valores em posições alternadas quando as comparamos:
- quando a moda=mediana=média temos uma distribuição de frequências razoavelmente simétrica;
- quando a moda \(\leq\) mediana \(\leq\) média (há uma quantidade maior de dados com grandes valores, arrastando a média para a direita, para cima) temos uma distribuição de frequências positivamente assimétrica, ; e,
- quando a moda \(\geq\) mediana \(\geq\) média (há uma quantidade maior de dados com pequenos valores, arrastando a média para a esquerda, para baixo) temos uma distribuição de frequências negativamente assimétrica.
barplot(tab_alturas,
main="Valores observados da alturas dos estudantes",
xlab="Altura (cm)",
ylab="Quantidade observada (un)",
ylim=c(0,6),
col="blue",
las=0,
hor="FALSE")
abline(v=mean(19.9, 21.1), col="red")
text( mean(19.9, 21.1)-0.5, 5, "Média=1,69 m", col = "red", srt=90)
abline(v=median(18.7 , 19.9), col="darkgreen")
text(median(18.7 , 19.9)-0.5, 5, "Mediana=1,675 m", col = "darkgreen", srt=90)
abline(v=c(16.3, 23.5), col="darkgrey")
text(c(16.3-0.5, 23.5-0.5), 5, c("Moda=1,66","Moda=1,73"), col = "darkgray", srt=90)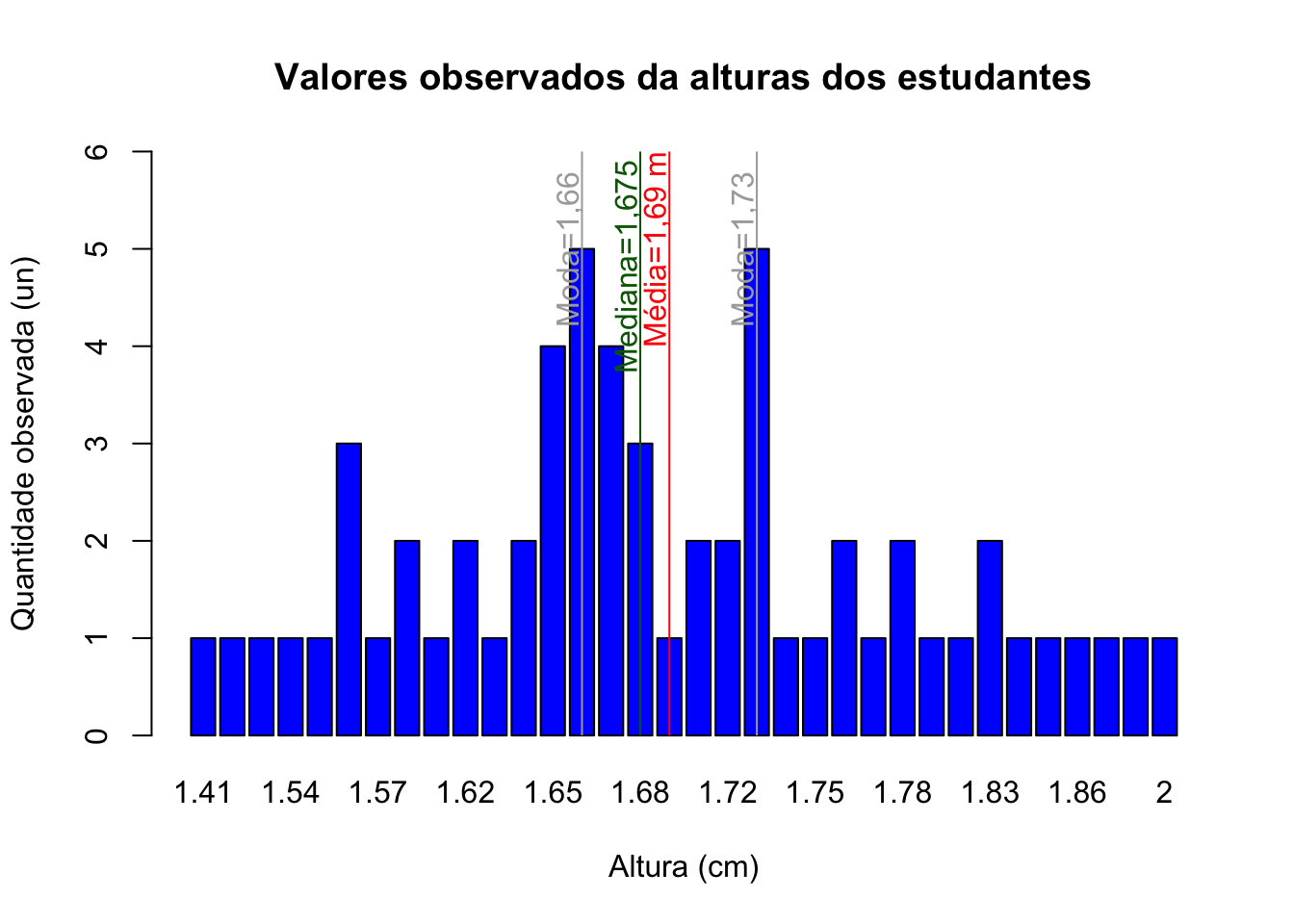
Figure 3.11: Valores observados das alturas dos estudantes e as posições da média, moda e mediana
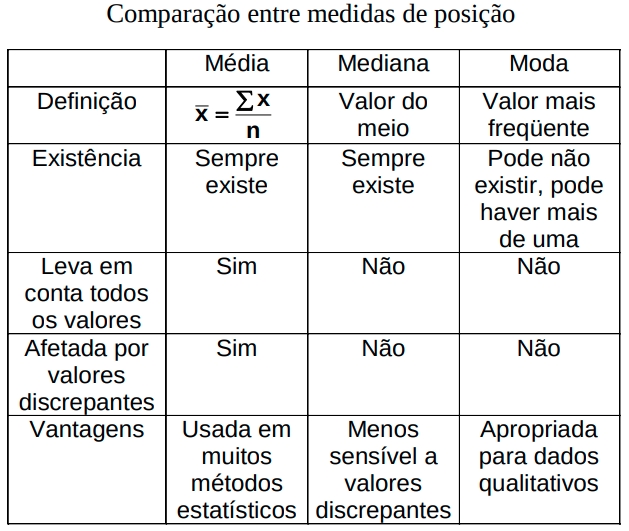
Figure 3.12: Quadro comparativo entre as medidas de tendência central (posição)