12.15 Verificações adicionais
- Análise de pontos com elevada capacidade de alavancar o modelo. A alavancagem mede o quanto uma observação \(x_{i}\) contribui para a predição de \(\hat{y}_{i}\) pelo modelo. Um ponto é considerado alavanca (leverage) quando este exerce uma forte influência no seu valor ajustado, sem com isso afetar a estimativa dos parâmetros do modelo. De modo análogo à distância de Cook, há diversos critérios para estabelecer um valor crítico para os hat values: \(h_{ii}\):
- \(h_{ii}\) > 2p/n (Hoaglin e Welsch, 1978),
- \(h_{ii}\) > 3p/n.
- Pontos discrepantes (\(outliers\)): A discrepância pode ser medida pela distância residual. Entretanto, os resíduos não são uma medida completa da discrepância. Para tanto basta-se imaginar casos onde onde uma observação possua elevada alavancagem que arraste o modelo inteiro em sua direção, resultando em pequenos resíduos. Uma forma de isolar esses pontos é dividindo seu resíduo por 1-\(h_{ii}\), obtendo-se a partir dessa expressão os resíduos \(studentizados\).
influentes: A estatística distância de Cook mede a influência de um determinado dado da amostra no que tange a quanto ele está afetando a linha de regressão, sendo medida pelo quanto a linha de regressão se alteraria caso esse dado fosse removido da da análise: ele exerce um destacado impacto da estimativa dos parâmetros do modelo. A influência na locação (afastamento de alguma observação da vizinhança do resto dos dados) pode ser investigada pelo gráfico feito das distâncias de Cook contra os valores ajustados. Há vários critérios para se estabelecer um valor limite para a estatística de Cook:\
\(D_{i}\) > 1 (Cook e Weisberg, 1982);
duas vezes a média das distâncias de Cook;
4/n < \(D_{i}\) < 1 (Bollen et al, 1990); ou,
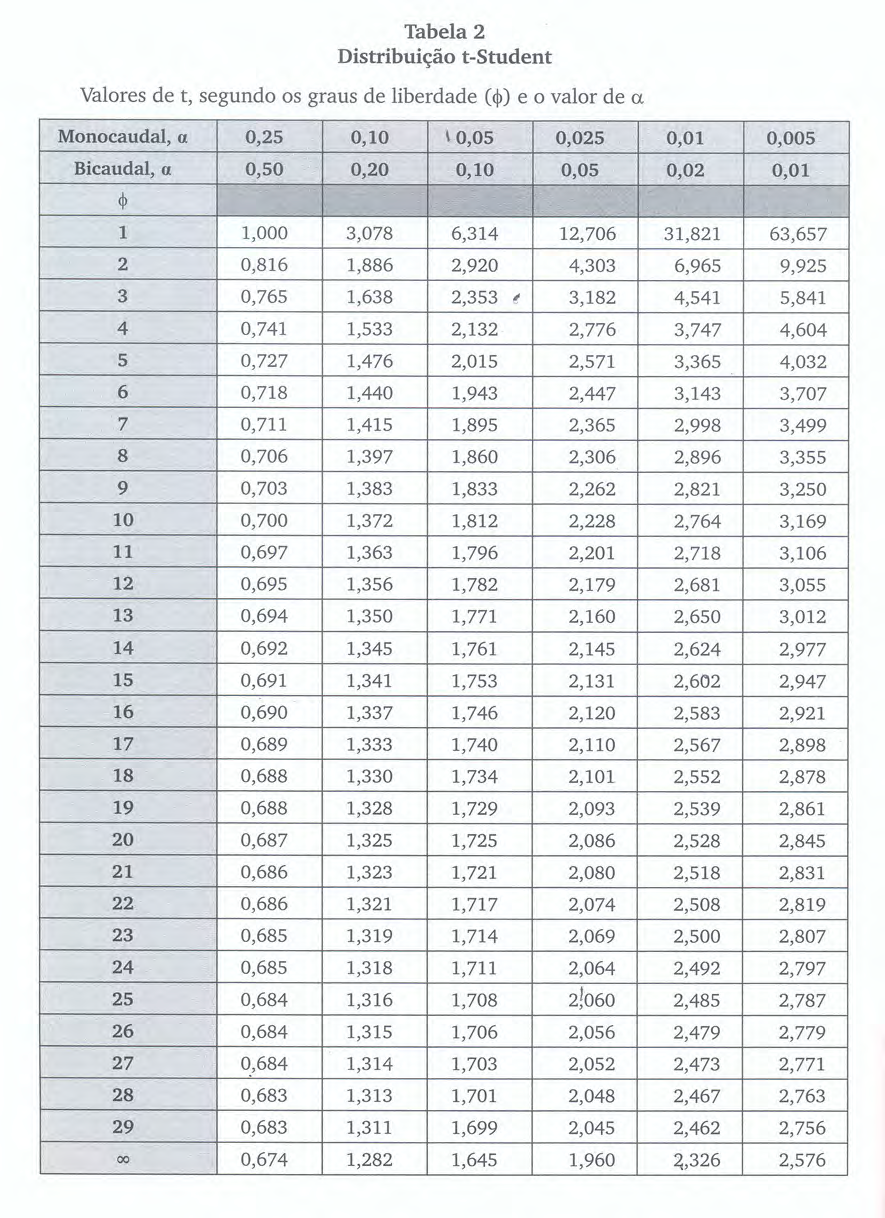
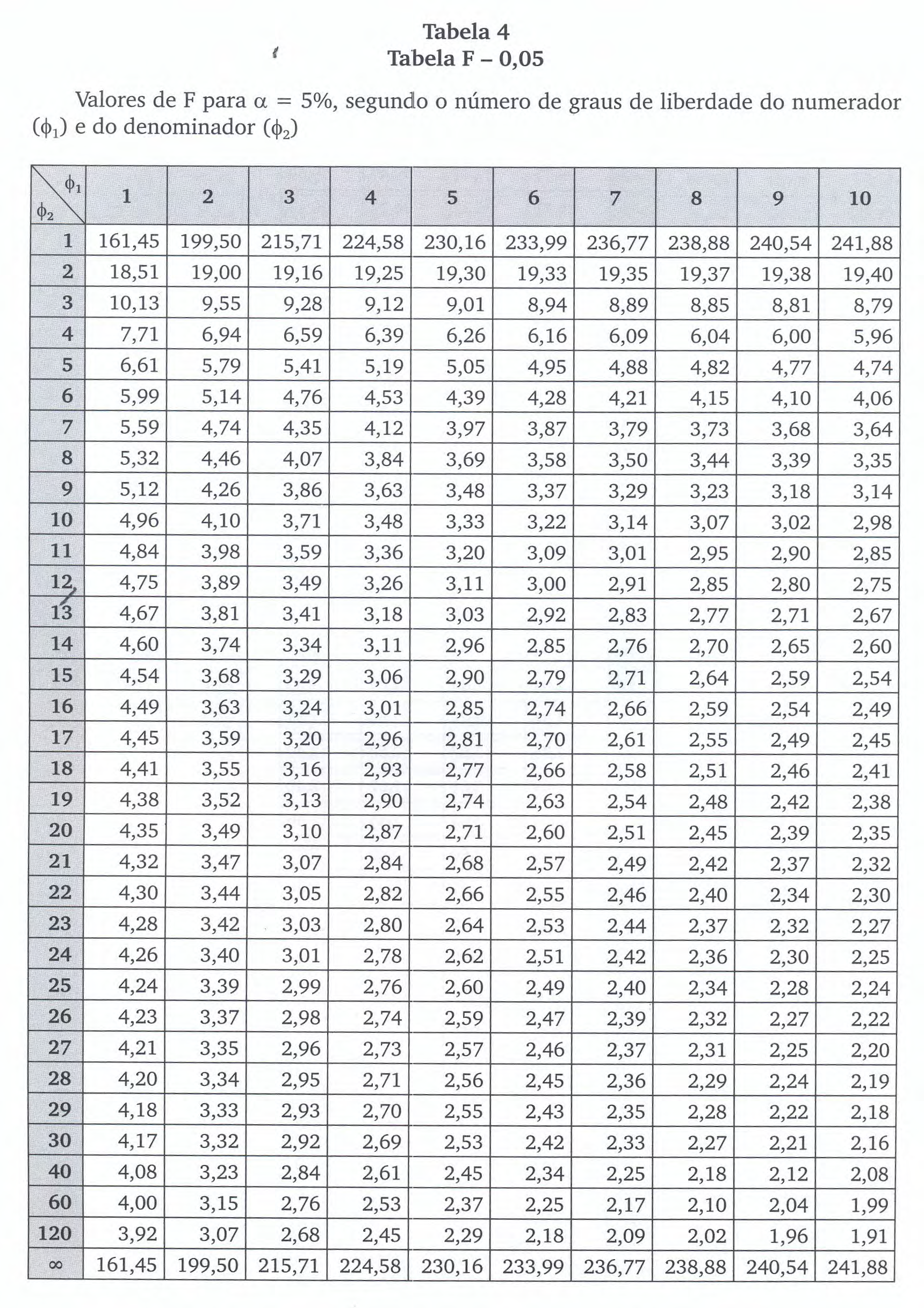
o valor crítico do quantil da distribuição F para uma significância igual a 0.5 com df1=p e f2=n-p.
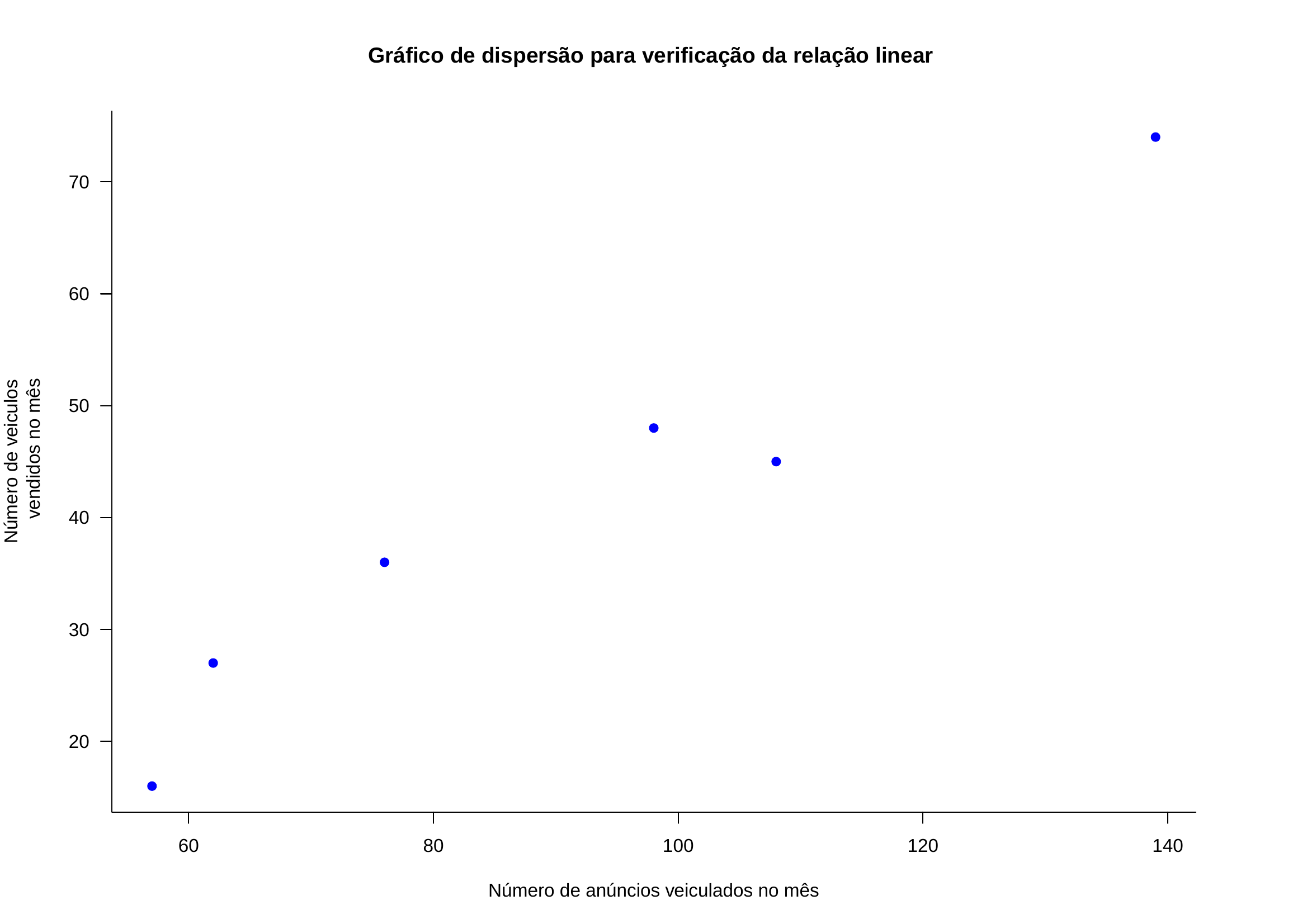
Exemplo 7: Um jornal deseja verificar a eficácia de seus anúncios na venda de carros usados e para isso realizou um levantamento de todos os seus anúncios e informações dos resultados obtidos pelas empresas que o contrataram e dele extraiu uma pequena amostra. A tabela abaixo mostra o número de anúncios e o correspondente número de veículos vendidos por 6 companhias que usaram apenas este jornal como veículo de propaganda. Estime os parâmetros de um modelo de regressão linear simples de \(X\) por \(Y\) verifique os pressupostos subjacentes ao método utilizado. Faça a análise dos resíduos e identifique possíveis \(outliers\) .
| Companhia | Anúncios feitos (X) | Carros vendidos (Y) |
|---|---|---|
| A | 74 | 139 |
| B | 45 | 108 |
| C | 48 | 98 |
| D | 36 | 76 |
| E | 27 | 62 |
| F | 16 | 57 |
Trazendo o modelo estimado anteriormente: \(\hat{y} = 27,844 + 1,5160 \cdot x\)
| Anúncios (X) | Carros vendidos (Y) | Valores estimados | Resíduos brutos | Resíduos padronizados |
|---|---|---|---|---|
| 74 | 139 | 140,028 | -1,028 | -0,1271 |
| 45 | 108 | 96,064 | 11,936 | 1,4762 |
| 48 | 98 | 100,612 | -2,612 | 0,3230 |
| 36 | 76 | 82,420 | -6,420 | 0,7940 |
| 27 | 62 | 68,776 | -6,776 | -0,8380 |
| 16 | 57 | 52,100 | 4,900 | 0,6060 |
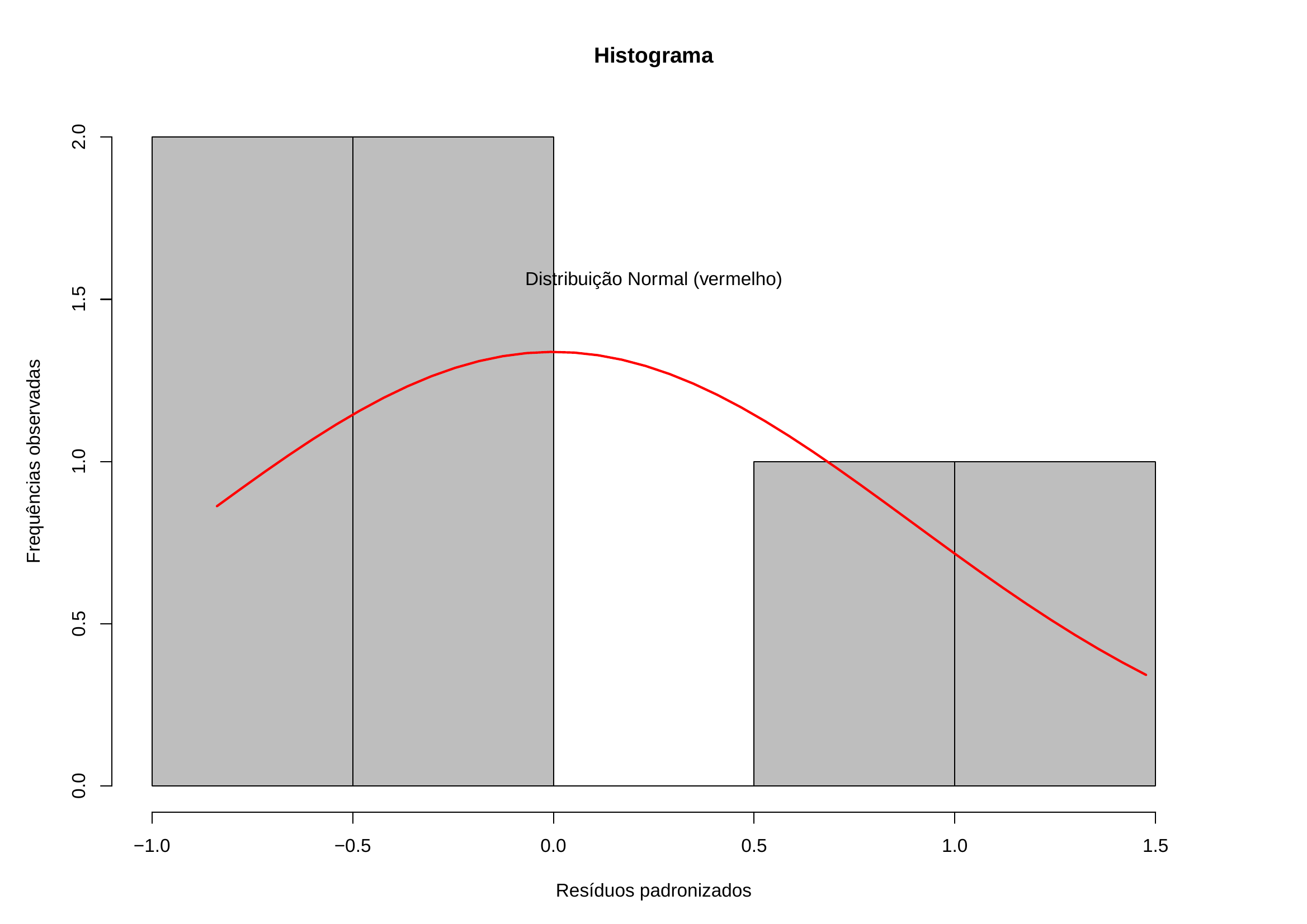
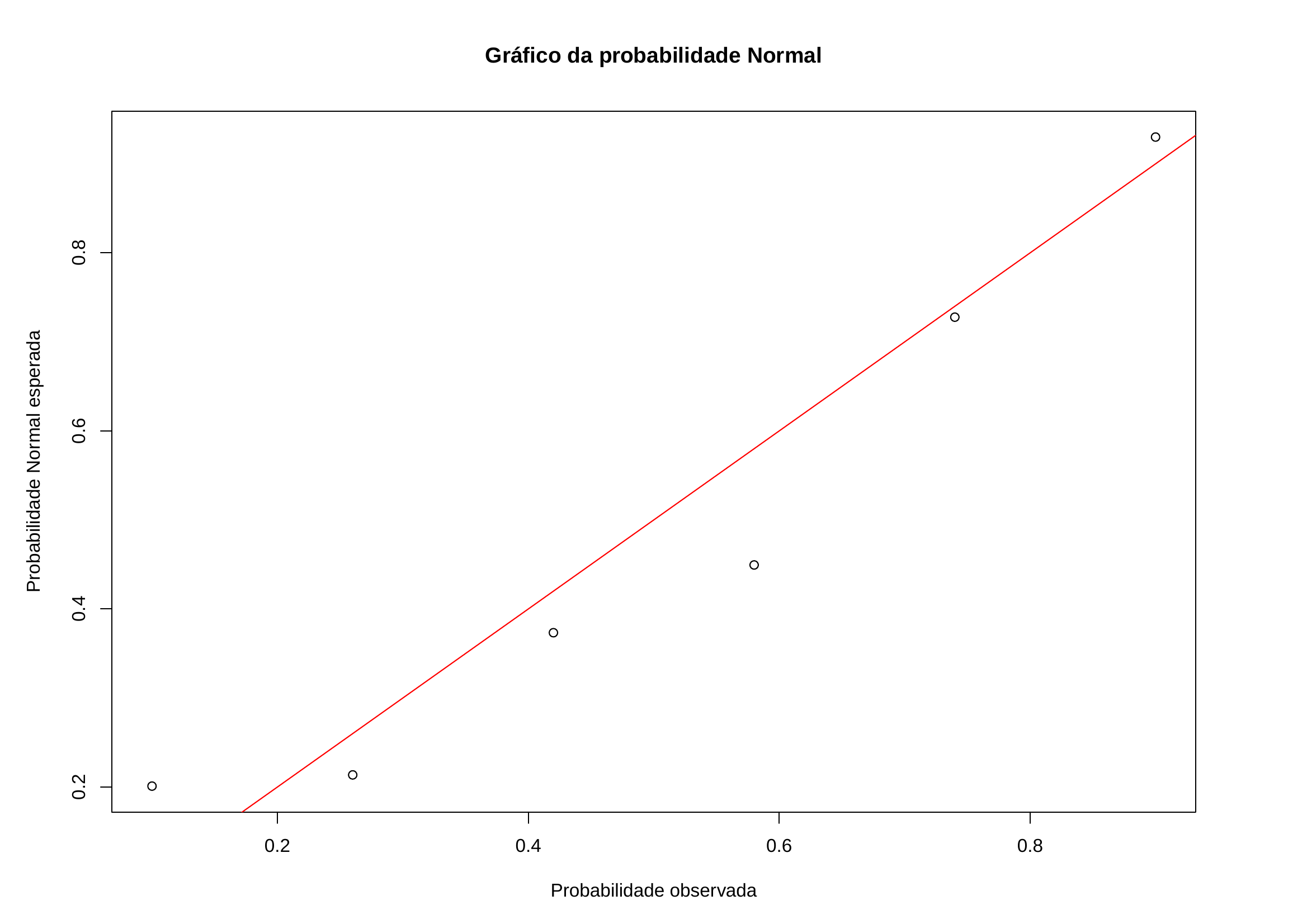
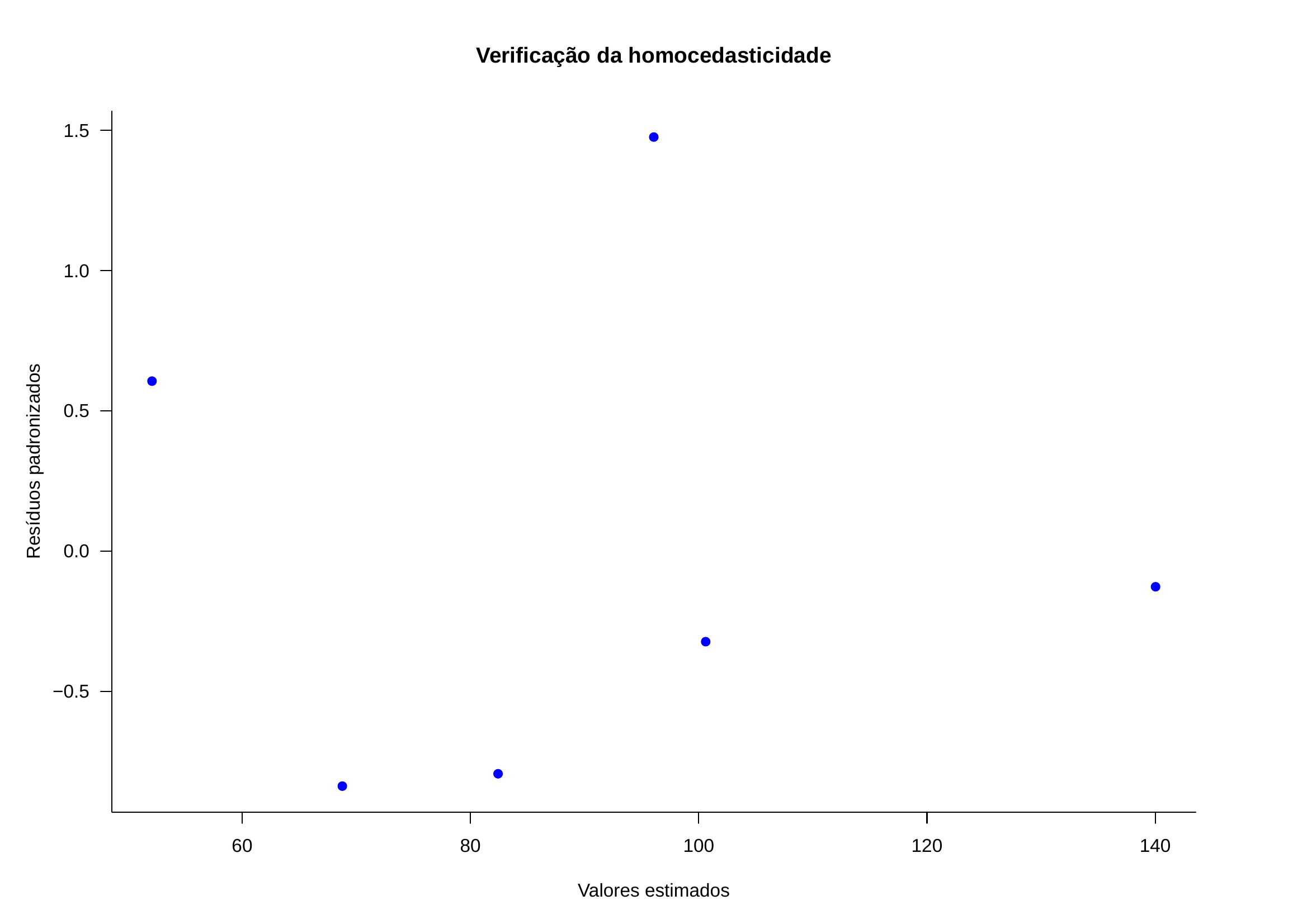
12.15.0.1 Roteiro básico para uma análise de regressão linear simples
- Definir o problema de pesquisa, selecionar a variável dependente e identificar a variável independente; ou seja, proceder a especificação do modelo. Aqui o pesquisador deve definir qual é a relação esperada entre a variável dependente e a independente;
- Maximizar o número de observações no sentido de aumentar o poder estatístico, a capacidade de generalização e reduzir toda sorte de problemas associados a estimação de parâmetros populacionais a partir de dados amostrais com \(n\) reduzido;
- Estimar um modelo;
- Verificar em que medida os dados disponíveis satisfazem os pressupostos da análise de regressão de mínimos quadrados ordinários. Como procedimento padrão, o pesquisador deve reportar as técnicas utilizadas para corrigir eventuais violações (transformações, re-codificações, aumento de \(n\), etc.);
- Interpretar os resultados, caso o modelo seja validado.
12.15.0.2 Homocedasticidade: transformações para estabilização da variância
Quando se observa que a distribuição gráfica dos resíduos não se mostra homocedástica, muitas vezes é útil aplicar uma transformação de Box-Cox para estabilizarmos a variância (torná-la constante independentemente do valor do resíduo).
Considerando \(X_{1}, ..., X_{n}\) os dados originais, a transformação de Box-Cox consiste em encontrar um \(\lambda\) tal que os dados transformados \(Y_{1}, ..., Y_{n}\) se aproximem de uma distribuição normal.
O modelo passa a assumir a forma: \(Y^{\lambda} = X \cdot \beta + \varepsilon\) com \(Y_{\lambda}\) sendo:
\[ \frac{Y^{\lambda} - 1}{\lambda} \text{ se } \lambda \ne 0 \\ ln (Y_{i}) \text{ se } \lambda = 0 \]
12.15.0.3 Transformações para linearização das relações
Algumas vezes as relações observadas entre a variável dependente e a independente não se mostram diretamente lineares.
Relações não-lineares podem ser linearizadas pela aplicação de transformações aos dados:
- Função hiperbólica: \(Y = \frac{X}{a \cdot X - b}\), pela forma transformada: \(\frac{1}{Y} = a - \frac{b}{X}\)
- Função exponencial: \(Y = a \cdot e^{b \cdot X}\), pela forma transformada: $Ln (Y) = Ln (a) + b X $
- Função potência: \(Y = a \cdot X ^{b}\), pela forma transformada: \(Ln (Y) = Ln (a) + b \cdot Ln (X)\)
12.15.0.5 Resolução do sistema de equações matriciais
Seja a matriz \(Y\) das observações realizadas na variável dependente \(Y_{i}\) (dimensão \(n \times 1\)):
\[ Y = \begin{pmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{pmatrix} \]
Seja a matriz \(X\) das observações realizadas na variável independente \(X_{i}\) (dimensão \(n \times 2\)):
\[ X = \begin{pmatrix} 1 & x_{1} \\ 1 & x_{2} \\ \vdots & \vdots \\ 1 & x_{n} \end{pmatrix} \]
Seja a matriz \(\beta\) dos parâmetros a serem estimados (dimensão: \(2 \times 1\)):
\[ \beta = \begin{pmatrix} \hat{\beta}_{0} \\ \hat{\beta}_{1} \end{pmatrix} \]
Seja a matriz \(e\) dos termos aleatórios (dimensão: \(n \times 1\)), não correlacionados, com média zero e variância constante:
\[ e = \begin{pmatrix} e_{1} \\ e_{2} \\ \vdots \\ e_{n} \end{pmatrix} \]
Então podemos escrever o seguinte sistema matricial:
\[ Y = X \cdot \hat{\beta} + e \]
A minimização da soma dos quadrados dos resíduos pode ser realizada fazendo-se:
\[ \Sigma (e_{i})^{2} = e^T \cdot e \]
O sistema acima tomará a forma:
\[ e = Y - X \cdot \hat{\beta} \]
\[ e^T \cdot e = (Y - X \cdot \hat{\beta})^T \cdot (Y - X \cdot \hat{\beta}) \]
Expandindo:
\[ Y^T \cdot Y - 2 \cdot \hat{\beta}^T \cdot X^T \cdot Y + \hat{\beta}^T \cdot X^T \cdot X \cdot \hat{\beta} \]
Minimizando os resíduos, obtemos a equação normal:
\[ (X^T \cdot X) \cdot \hat{\beta} = X^T \cdot Y \]
Multiplicando ambos os lados por \((X^T \cdot X)^{-1}\):
\[ (X^T \cdot X)^{-1} \cdot (X^T \cdot X) \cdot \hat{\beta} = (X^T \cdot X)^{-1} \cdot X^T \cdot Y \]
Por fim, considerando-se que \((X^T \cdot X)^{-1} \cdot (X^T \cdot X) = I\), obtemos a solução para \(\hat{\beta}\):
\[ \hat{\beta} = (X^T \cdot X)^{-1} \cdot X^T \cdot Y \]