5.2 Função de densidade de probabilidade (Probability Density Function - PDF)

Considerem os espaços amostrais a seguir ($\Omega_{1},\Omega_{2},\Omega_{3},\Omega_{4},\Omega_{5}$) representativos de 4 experimentos aleatórios e admitam também que todos os eventos possíveis são equiprováveis.

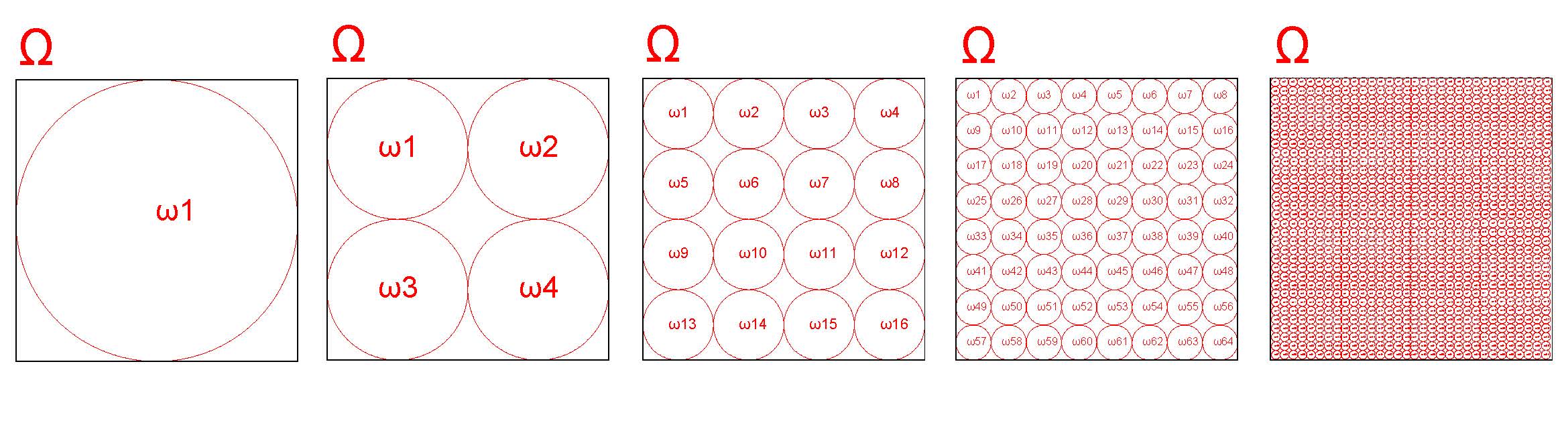
Figure 5.2: Diferentes espaços amostrais de um experimento aleatório (por razões gráficas desprezem o espaço fora dos círculos

Interpretem o último deles como um espaço amostral formado por $\infty$ pontos amostrais.

Os eventos que compõem os quatro primeiros espaços amostrais são variável aleatória discretas.

Discretas pois permitem a contagem dos possíveis valores (finitos ou infinitos contáveis) aleatórios que o experimento pode assumir. Mas no quinto espaço amostral temos incontáveis possibilidades.

Um espaço amostral com essa característica é representativo de uma variável aleatória contínua.

Sendo todos os eventos representados nos espaços amostrais equiprováveis, comparemos as probabilidades associadas a cada um desses possíveis resultados.

Em $\Omega_{1}$, $P(\omega_{1})=1$
Em $\Omega_{2}$, $P(\omega_{1})=P(\omega_{2})=P(\omega_{3})=P(\omega_{4})=0,50$
Em $\Omega_{3}$, $P(\omega_{1})=P(\omega_{2})=...=P(\omega_{16})=0,0625$
Em $\Omega_{4}$, $P(\omega_{1})=P(\omega_{2})=...=P(\omega_{64})=0,015625$
Em $\Omega_{5}$, $P(\omega_{n}) \rightarrow 0$, à medida que o número de eventos $n \rightarrow \infty$

A probabilidade individual de qualquer evento do quinto espaço amostral ocorrer $\rightarrow 0$.

Por essa razão, no caso de variáveis aleatórias contínuas, não faz sentido falar em uma probabilidade pontual exata, associada a um resultado específico. Isso ocorre porque, para qualquer valor particular, a probabilidade é sempre igual a zero.

Experimentos aleatórios nos quais os possíveis resultados assumem valores resultantes de processos de mensuração tais como, por exemplo, rendas, pesos, velocidades, tempos, comprimentos, pertencentes aos números Reais, podem ser adequadamente modelados por variáveis aleatórias contínuas.

Para estes uma função densidade de probabilidade é definida de modo a retornar a probabilidade de ocorrência associada a um intervalo de valores, posto a probabilidade exata de ocorrência de um valor aleatório contínuo tender a zero ($P(X=x) \to 0$).

A função $f(x)$ é uma função densidade de probabilidade para a variável aleatória contínua $X$ se atende às seguintes condições relacionadas aos axiomas da probabilidade:

1- $f(x) \geq 0$, para todo $x \in (-\infty, \infty)$;
2- A integral da função sobre todo o domínio é igual a 1:

\[ \underset{-\infty }{\overset{\infty }{\int }}f\left(x\right)dx = 1 \].

Se $X$ é uma variável aleatória contínua, a probabilidade de $X$ assumir qualquer valor exato é $P(X = x) = 0$. No entanto, a probabilidade intervalar de $X$ estar entre dois valores distintos, $a$ e $b$, é dada por:

\[ P(a < X < b) = \int_{a}^{b} f(x) \, dx. \]

Graficamente, a interpretação de uma função densidade de probabilidade contínua é representada pela área sob a curva da função $f(x)$, delimitada pelos valores de interesse $a$ e $b$. Essa área corresponde à probabilidade de $X$ estar no intervalo $(a, b)$.

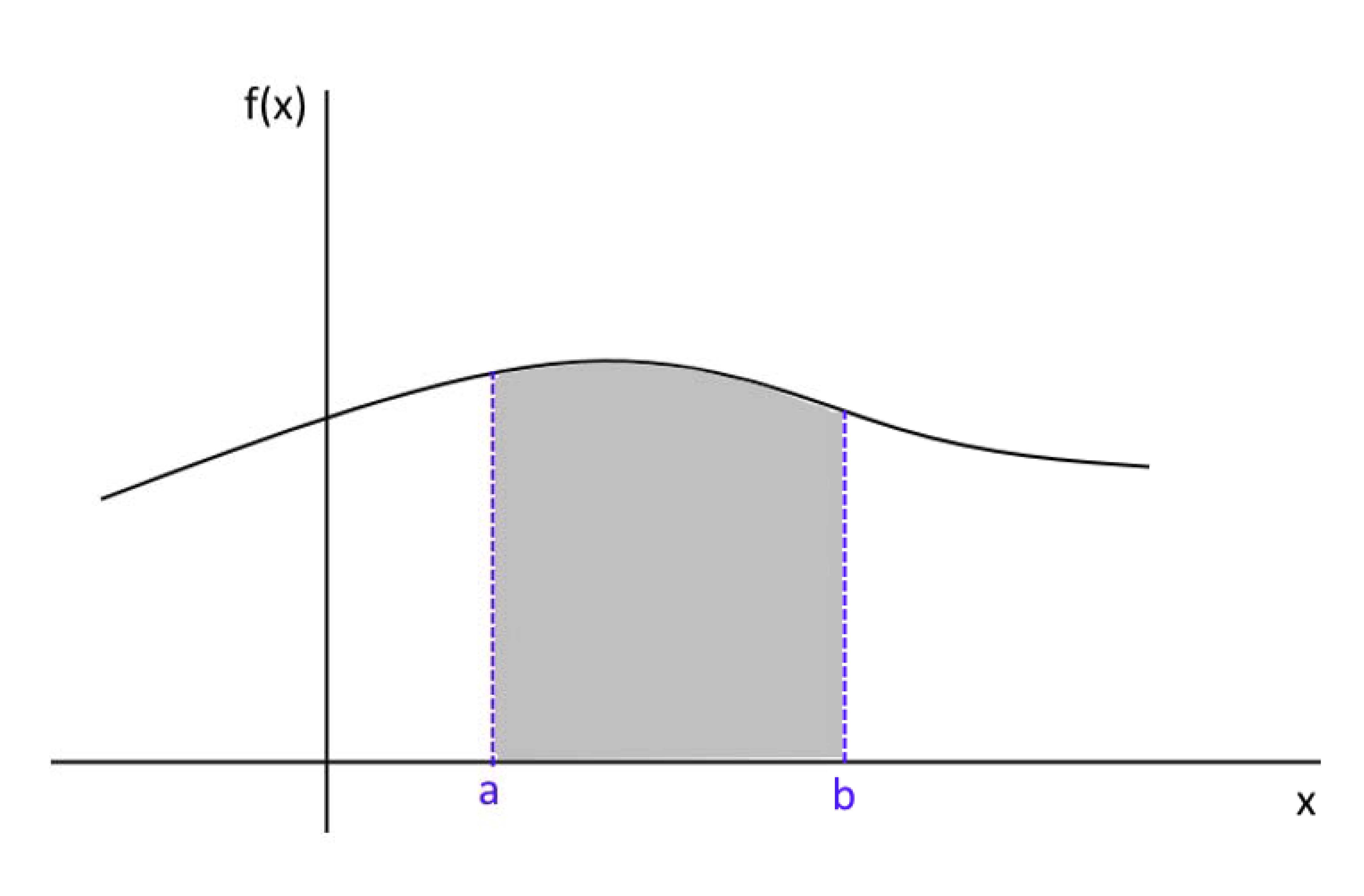
A área sob a curva de uma função de probabilidade de uma variável contínua entre dois valores quaisquer é a probabilidade de se observar valores entre esses dois pontos

Figure 5.3: A área sob a curva de uma função de probabilidade de uma variável contínua entre dois valores quaisquer é a probabilidade de se observar valores entre esses dois pontos

Como $f(x) \geq 0$, a curva da função densidade de probabilidade estará acima do eixo $x$ e a totalidade da área será igual a $1$, conforme

\[ \underset{-\infty }{\overset{\infty }{\int }}f\left(x\right)dx = 1. \]

A função $f(x)$ é uma função densidade de probabilidade para a variável aleatória contínua $X$ se atende às seguintes condições relacionadas aos axiomas da probabilidade:

Para tornar o conceito de densidade mais compreensível admita a função densidade de probabilidade (fdp) a seguir e sua representação gráfica na Figura 5.4

\[ f(X=x)= \begin{cases} 2 . x \hspace{0.6cm} \text{para } 0 \le x \le 1 \\ 0, \hspace{0.9cm} \text{para qualquer outro x}\\ \end{cases} \]

$A área definida por (ODA) equivale à probabilidade de $f(X=x)$ no intervalo $0 \le x \le 0,50$ é notadamente menor que a área definida por (ABCD) equivalente à probabilidade de $f(X=x)$ no intervalo $0,5 \le x \le 1$. Tendo os intervalos [0;0,50] e [0,50; 1,00] igual amplitude, depreende-se que uma fdp é uma função indicadora da concentração massa (probabilidade) nos possíveis valores de $X$$

Figure 5.4: A área definida por (ODA) equivale à probabilidade de $f(X=x)$ no intervalo $0 \le x \le 0,50$ é notadamente menor que a área definida por (ABCD) equivalente à probabilidade de $f(X=x)$ no intervalo $0,5 \le x \le 1$. Tendo os intervalos [0;0,50] e [0,50; 1,00] igual amplitude, depreende-se que uma fdp é uma função indicadora da concentração massa (probabilidade) nos possíveis valores de $X$

A função de distribuição cumulativa, definida como $F(x) = P(X \leq x)$, também terá a forma de uma curva, crescente, que aumenta continuamente de $0$ para $1$. Essa característica reflete o fato de que, ao longo do eixo $x$, a probabilidade cumulativa acumula todos os valores de $f(x)$ até $x$, de modo que:

$F(x)$ é não decrescente ($F(x_1) \leq F(x_2)$ para $x_{1} \leq x_{2}$);
$F(x)$ atinge valores-limite:

\[ \lim_{x \to -\infty} F(x) = 0 \quad \text{e} \quad \lim_{x \to \infty} F(x) = 1. \]

Assim, $F(x)$ descreve graficamente a probabilidade acumulada até qualquer valor $x$, reforçando a relação entre a densidade de probabilidade e a probabilidade cumulativa.

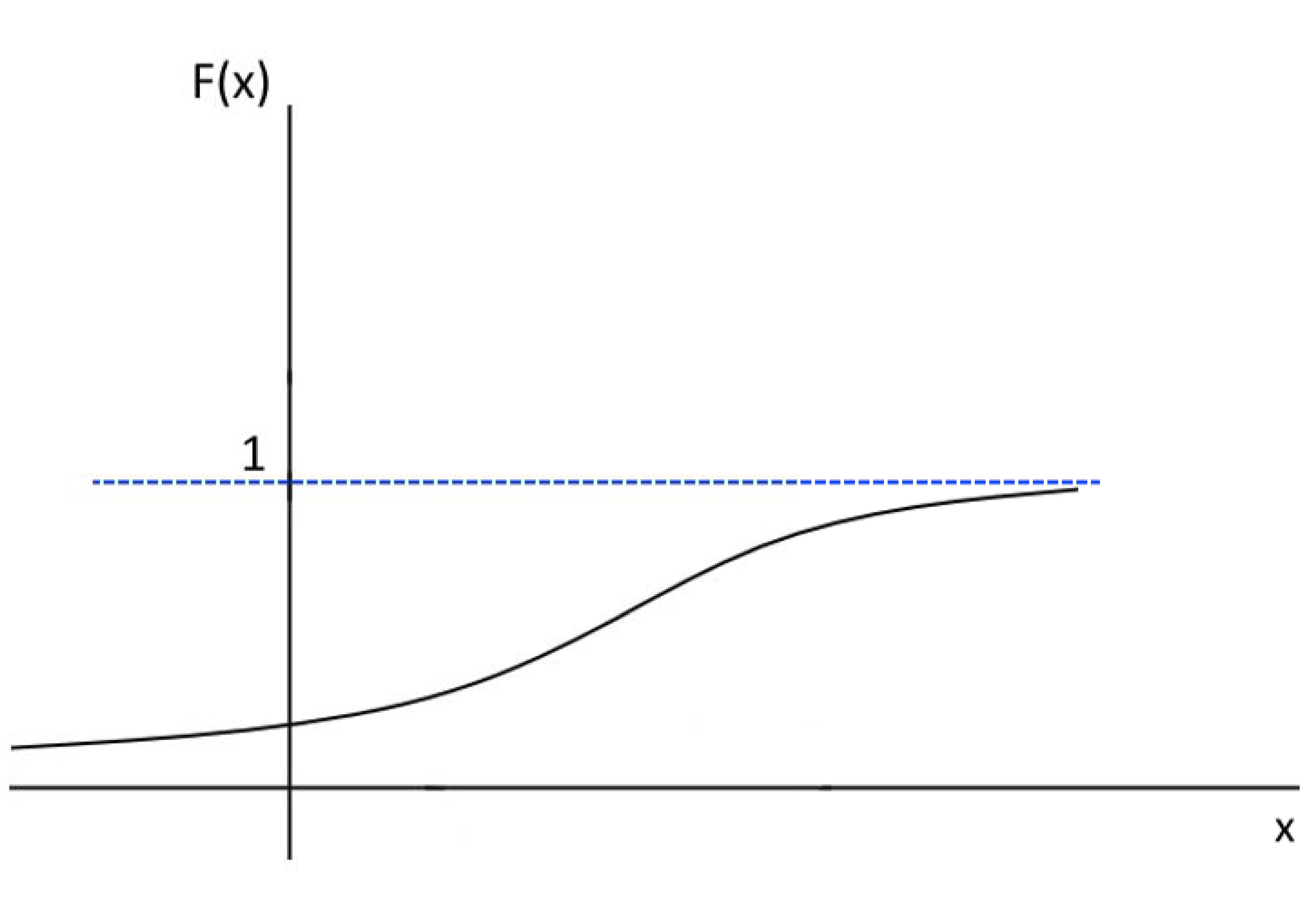
Figure 5.5: Função de probabilidade cumulativa

Exemplo: Seja a seguinte função e verifique se a função $f(x)$ pode ser a função de densidade de probabilidade da variável aleatória contínua $X$ e determine qual a probabilidade associada a valores compreendidos no intervalo $0 \leq X \leq \frac{1}{2}$.

A resolução deste exemplo será feita de um modo geométrico.

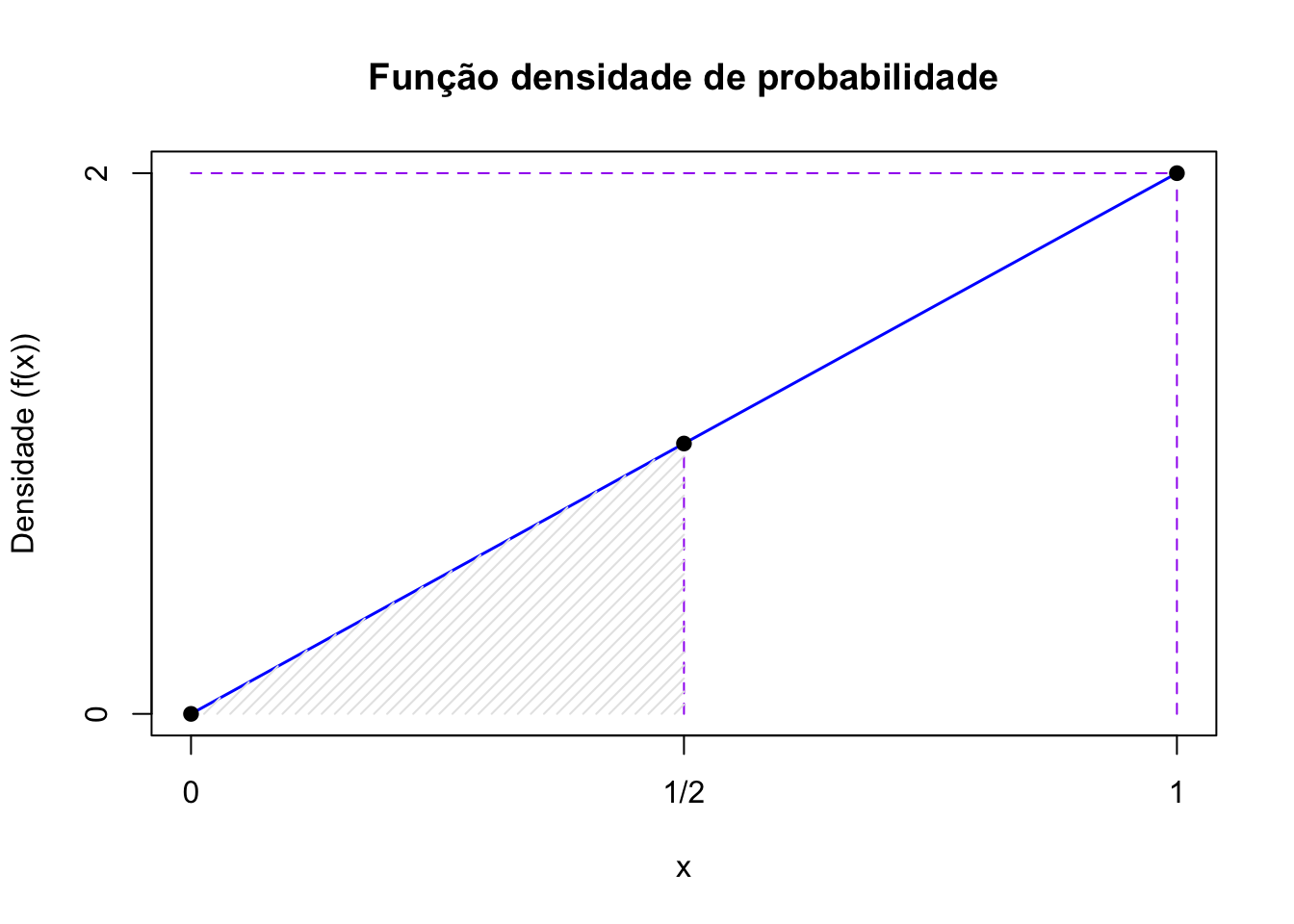
Figure 5.6: A probabilidade de se observar valores entre 0 e 1/2 é igual à area sob a função densidade de probabilidade entre esses dois valores

Verificações para se aceitar a função como uma função de densidade de probabilidade para a variável aleatória $X$:

\[ f(x) \geq 0 \]

\[ \underset{-\infty }{\overset{\infty }{\int }}f\left(x\right)dx = 1 \]

Resp.: Atende às duas condições (não assume valores menores que zero e a área sob a reta dessa função é unitária)

Cálculo da probabilidade para o intervalo $0 \leq X \leq \frac{1}{2}$ a partir da área do triângulo hachurado ($\frac{base \times altura}{2}$):

\[ P ( 0 \leq X \leq \frac{1}{2}) = \frac{1}{2} \times (\frac{1}{2} \times 1 ) = \frac{1}{4} \]

Exemplo: Verifique se as funções a seguir atendem os pressupostos necessários para ser uma função densidade de probabilidade (assuma que toda $f(x)=0$ para valores fora dos intervalos especificados):

1- $f(x)=3x$ para $0 \le x \le 1$;
2- $f(x)=\frac{x^{2}}{2}$ para $x \ge 0$;
3- $f(x) = \frac{(x-3)}{2}$ para $3 \le x \le 5$;
4- $f(x)=2$ para $0 \le x \le 2$;
5-

\[ f(X=x)= \begin{cases} \frac{(2+x)}{4}, \hspace{0.6cm} \text{para } -2 \le x \le 0 \\ \frac{(2-x)}{4}, \hspace{0.6cm} \text{para } 0 \le x \le 2\\ \end{cases} \] 6- $f(x)=- \pi$ para $-\pi < x < 0$

Os gráficos das funções densidade de probabilidade são:

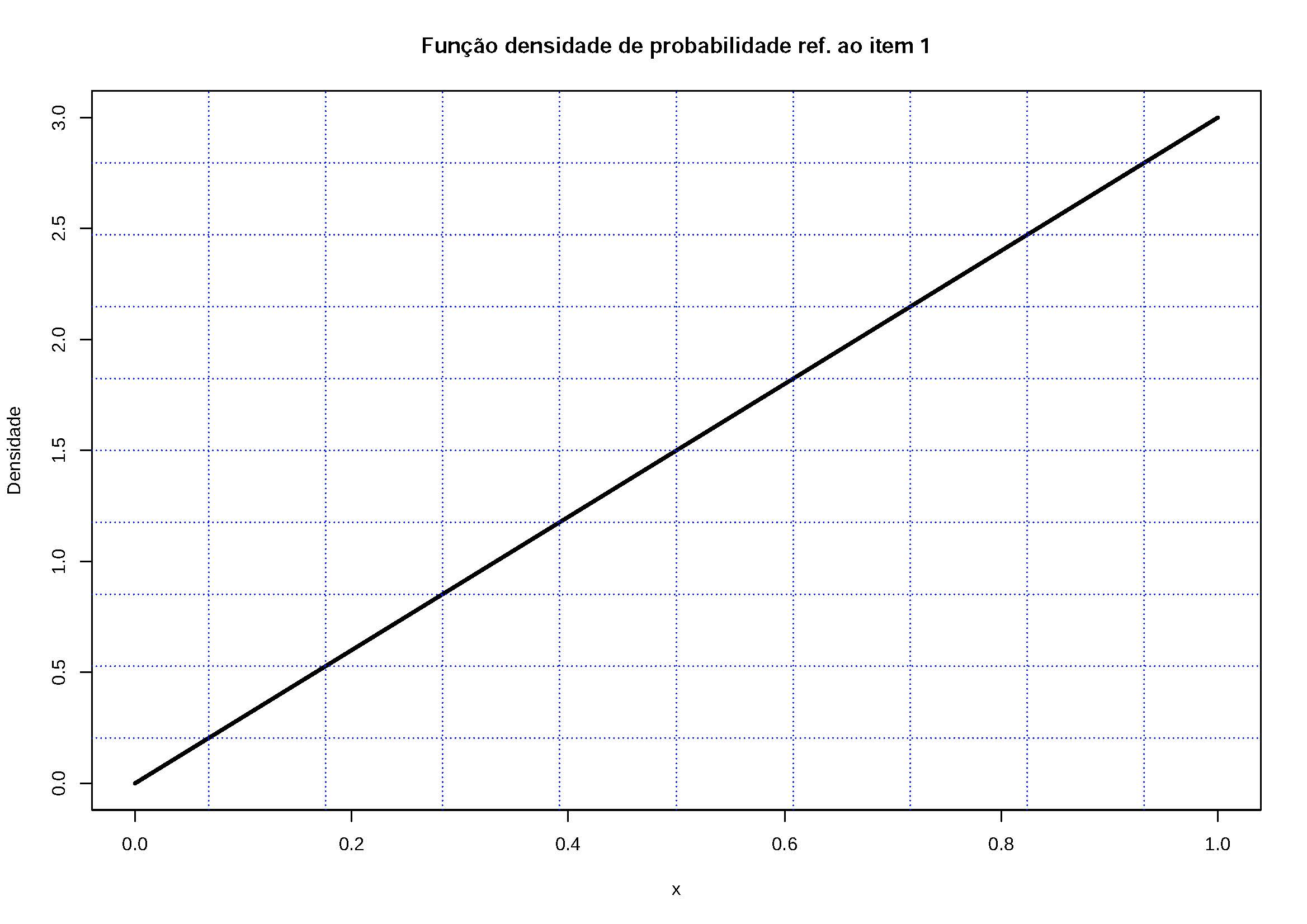
$A área definida por $f(x)$ no intervalo $0 \le x \le 1$ é maior que 1. Por essa razão não pode ser uma fdp$

Figure 5.7: A área definida por $f(x)$ no intervalo $0 \le x \le 1$ é maior que 1. Por essa razão não pode ser uma fdp

$A área definida por $f(x)$ no intervalo $x \ge 0$ é maior que 1. Por essa razão não pode ser uma fdp$

Figure 5.8: A área definida por $f(x)$ no intervalo $x \ge 0$ é maior que 1. Por essa razão não pode ser uma fdp

$Os valores assumidos por $f(x)$ são $\ge 0$ e a área definida por f(x) o intervalo $3 \le x \le 5$ é igual a 1. Por essa razão pode ser uma fdp$

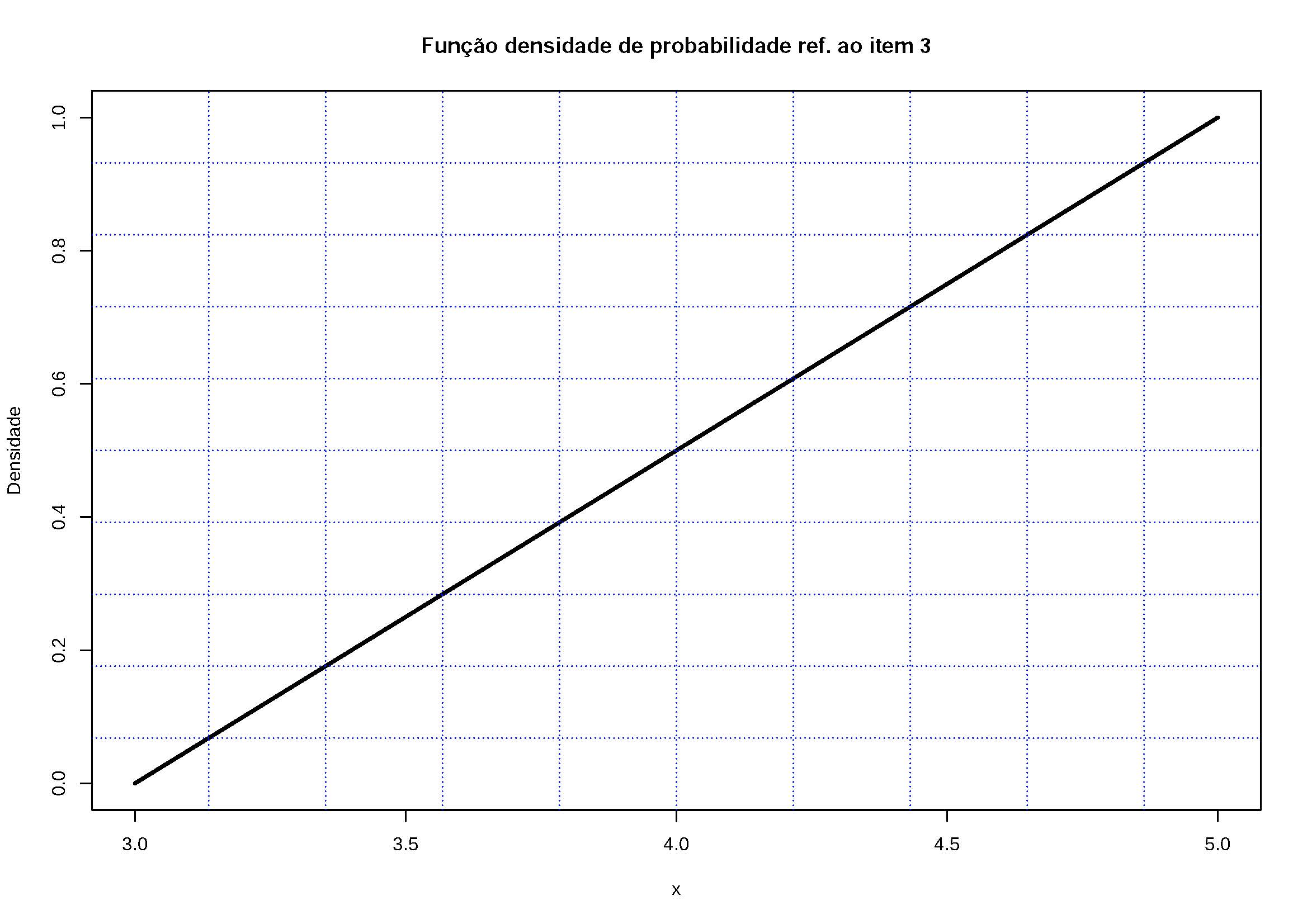
Figure 5.9: Os valores assumidos por $f(x)$ são $\ge 0$ e a área definida por f(x) o intervalo $3 \le x \le 5$ é igual a 1. Por essa razão pode ser uma fdp

$A área definida por $f(x)$ no intervalo $0 \le x \le 2$ é maior que 1. Por essa razão não pode ser uma fdp$

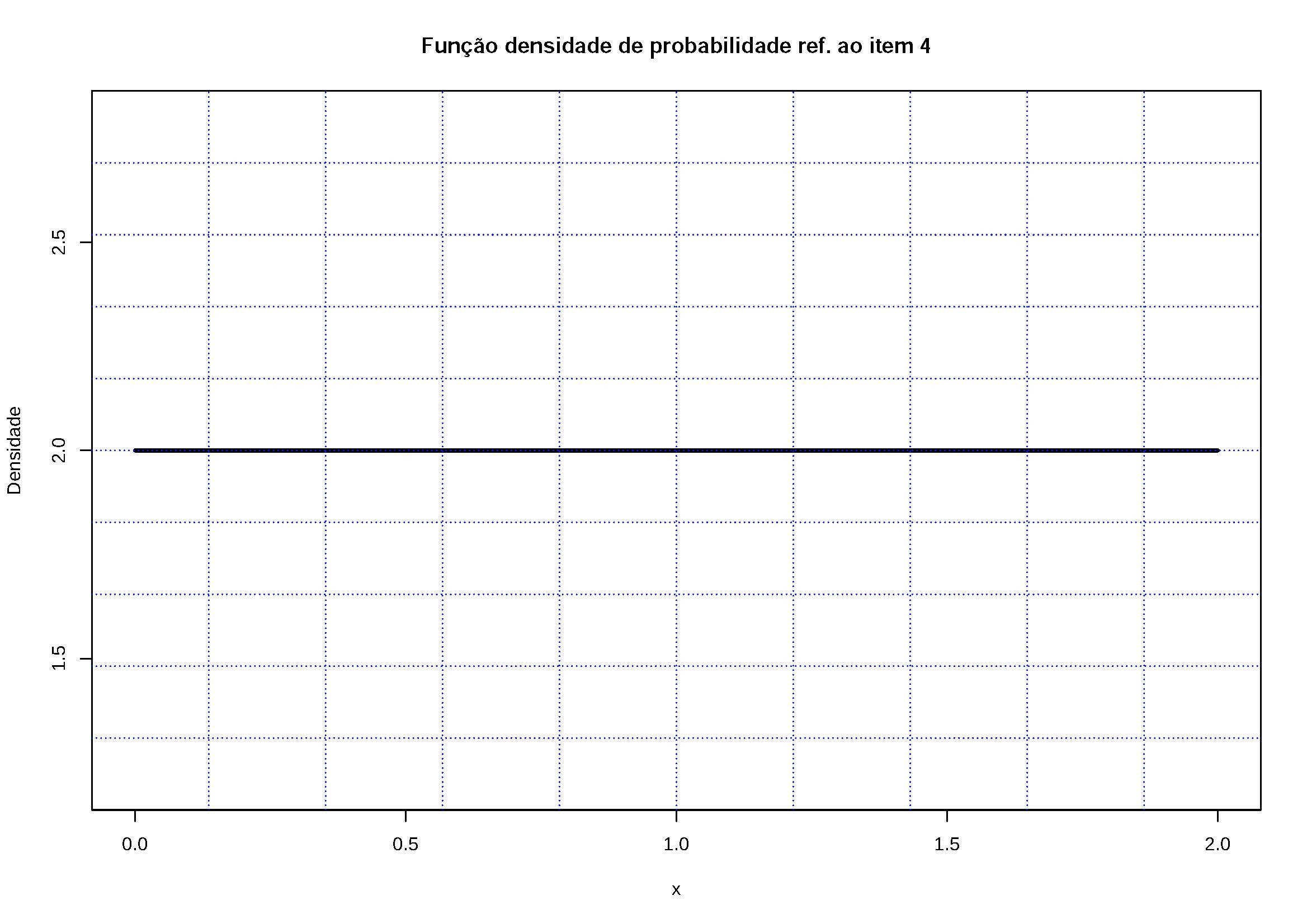
Figure 5.10: A área definida por $f(x)$ no intervalo $0 \le x \le 2$ é maior que 1. Por essa razão não pode ser uma fdp

$Os valores assumidos por $f(x)$ são $\ge 0$ e a área definida por $f(x)$ nos intervalos $-2 \le x \le 0$ e $0 \le x \le 2$ é igual a 1. Pode ser uma fdp$

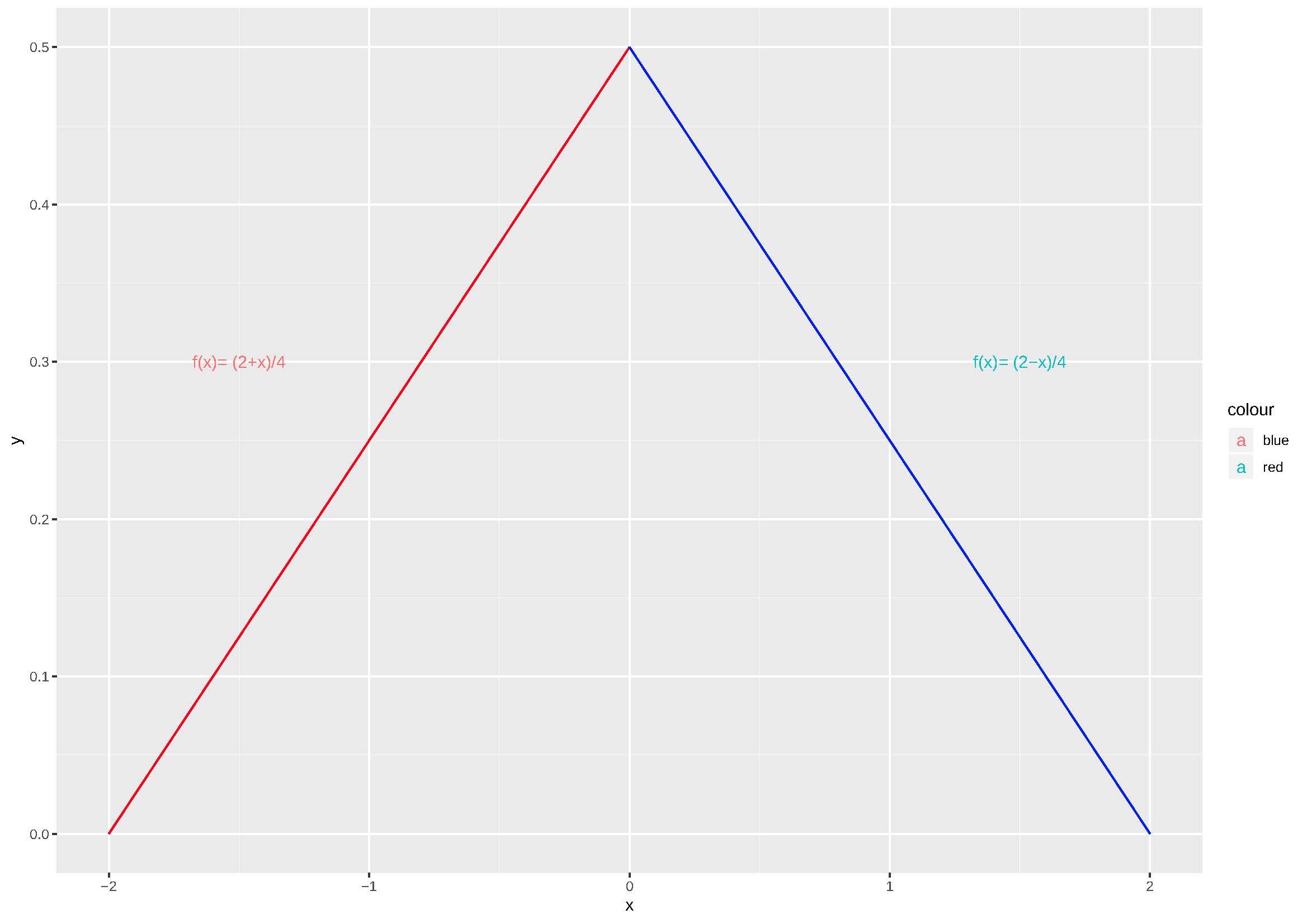
Figure 5.11: Os valores assumidos por $f(x)$ são $\ge 0$ e a área definida por $f(x)$ nos intervalos $-2 \le x \le 0$ e $0 \le x \le 2$ é igual a 1. Pode ser uma fdp

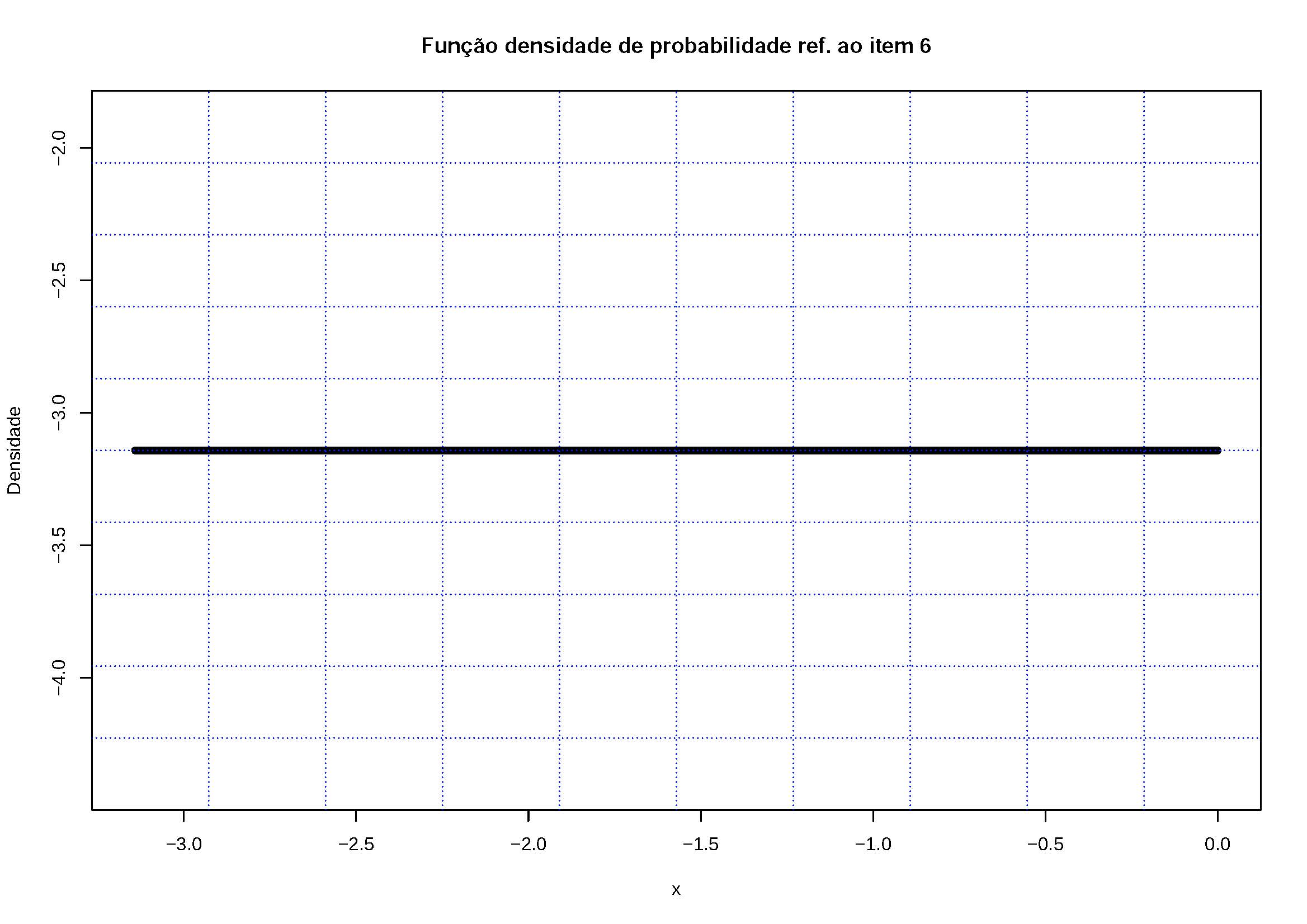
Figure 5.12: Os valores assumidos por f(x) são $<0$. Por esa razão não pode ser uma fdp.

Exemplo: A dureza $X$ de uma peça de aço pode ser entendida como sendo uma variável aleatória contínua uniforme no intervalo $(50,70)$ da escala Rockwel. Calcule a esperança e a variâcia dessa variável aleatória e a probabilidade de que uma peça tenha dureza entre 55 e 60?

Definindo a variável aleatória contínua $X:X \sim U(50,70)$:

\[ f(X=x)= \begin{cases} \frac{1}{70-50}=\frac{1}{20}, \hspace{0.6cm} \text{para } 50 \le x \le 70 \\ 0, \hspace{1cm} \text{para qualquer outro x}\\ \end{cases} \]

Sua esperança e a variância são:

Esperança: $E(X) = \mu = \frac{(70+50)}{2}=60$; e,
Variância: $Var(X) = \frac{(70-50)^{2} }{12}=33,33$.

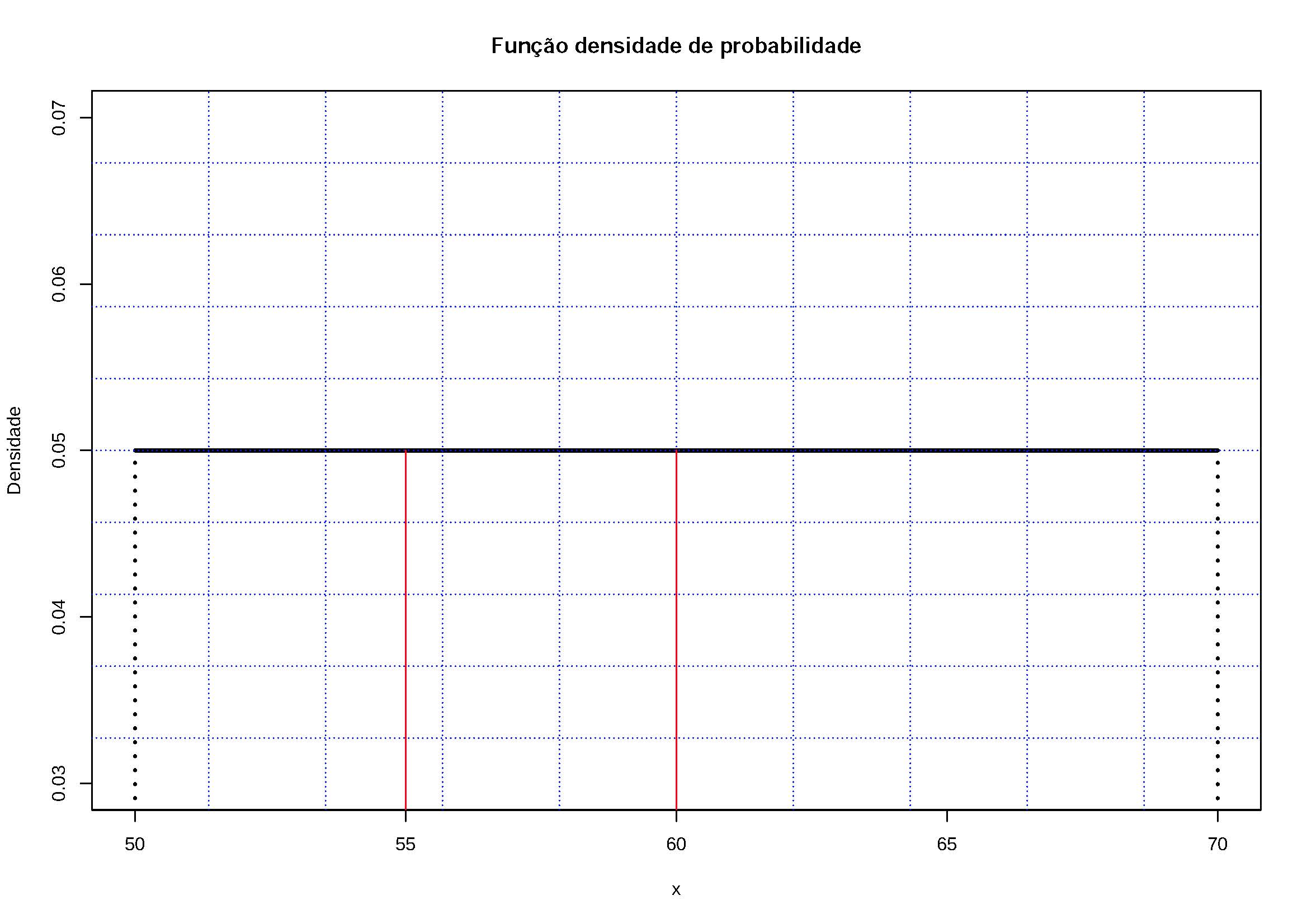
$Os valores assumidos por $f(x)$ são $\ge 0$ e a área definida por $f(x)$ no intervalo $50 \le x \le 70$ é igual a 1. Por essa razão pode ser uma fdp. A probabilidade pedida equivale à área $P(60 \le x \le 55) = (60-55) . 0,05=0,25$.$

Figure 5.13: Os valores assumidos por $f(x)$ são $\ge 0$ e a área definida por $f(x)$ no intervalo $50 \le x \le 70$ é igual a 1. Por essa razão pode ser uma fdp. A probabilidade pedida equivale à área $P(60 \le x \le 55) = (60-55) . 0,05=0,25$.