10.2 Distribuição das proporções amostrais

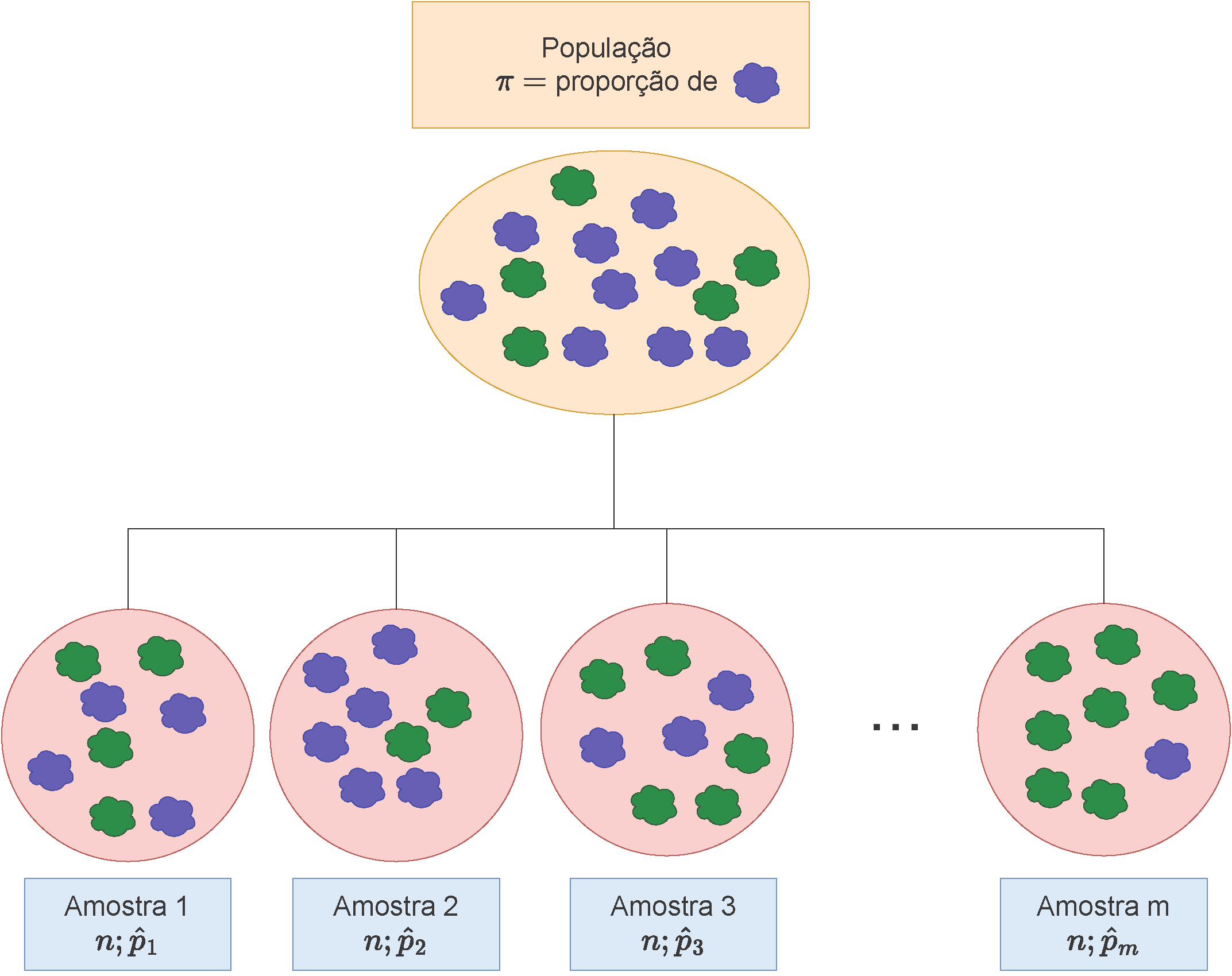
$Ilustração de $m$ amostras de mesmo tamanho ($n$) extraídas de uma mesma população onde a característica de interesse se manifesta sob uma proporção populacional $\pi$$

Figure 10.1: Ilustração de $m$ amostras de mesmo tamanho ($n$) extraídas de uma mesma população onde a característica de interesse se manifesta sob uma proporção populacional $\pi$

Para estudarmos a distribuição das proporções amostrais ($\hat{p}$) considerem uma população apresentando uma determinada característica de interesse com proporção $\pi$. Essa característica de interesse assume apenas duas possibilidades em cada elemento da população: ela pode ou não estar presente:

\[ X_{i}= \begin{cases} 1, \text{ se o i-ésimo elemento é portador da característica}\\ 0, \text{ se o i-ésimo elemento não é portador da característica}\\ \end{cases} \]

Assim, ao se escolher ao acaso um elemento da população, a probabilidade dessa característica estar presente pode ser estimada seguindo o modelo teórico de uma variável de Bernoulli e assim $X_{i} \sim Ber(\pi)$ e, como tal, $E(X)=\pi$ e $Var(X)=\pi(1-\pi)$.

Repetindo-se essa ``extração’’ por $n$ vezes podemos definir a variável aleatória $Y_{n}$ como sendo o número de sucessos observados em $n$ repetições de Bernoulli:

\[ Y_{n}= X_{1} + \dots + X_{n} \]

e assim, $Y_{n} \sim Bin(n, \pi)$ e a proporção amostral observada de sucessos ao final das $n$ repetições será a média:

\[ \hat{p}=\frac{Y}{n}=\frac{X_{1} + \dots + X_{n}}{n} \].

em que $\hat{p}$ é uma estimativa amostral da proporção populacional $\pi$.

Demonstra-se que para:

um razoável número de repetições: $n \ge 30$;
de uma população onde a proporção $\pi$ não é extrema: próximas a 0 ou 1; e tal que
$(n \cdot \pi)$ e $(n \cdot (1-\pi))$ sejam maiores que 15 (alguns autores consideram limites mais brandos, iguais a 10 ou ainda a 5),

ao se repetir o experimento anotando-se as proporções amostrais $\hat{p}$ obtida em cada uma das $n$ repetições de Bernoulli , o perfil da curva de distribuição dessas proporções amostrais torna-se razoavelmente simétrico à medida que o número $n$ de repetições de Bernoulli cresce, para qualquer que seja a proporção populacional, e oscila em torno de $\pi$.

Pelo Teorema de DeMoivre e Laplace (anteriores ao Teorema do Limite Central), demonstra-se que, para um grande número de repetições ($n$), o valor esperado e a variância das proporções amostrais são:

\[\begin{align*} E(Y) & =n \cdot \pi \\ Var(Y) & =n \cdot \pi \cdot (1-\pi) \end{align*}\]

e a distribuição das proporções amostrais será aproximadamente Normal com parâmetros $\mu=n.\pi$ e $\sigma^{2}=n.\pi.(1-\pi)$:

\[ Y \sim N \left( n\cdot\pi ; n\cdot\pi\cdot(1-\pi) \right) \]

Uma vez que a proporção amostral está definida como: $\hat{p} = \frac{Y_{n}}{n}$ segue-se que o valor esperado $\hat{p}=\mu$:

\[\begin{align*} E(\hat{p}) & = E(\frac{Y}{n}) \\ & = \frac{1}{n} \cdot E(Y) \\ & = \frac{1}{n} \cdot n \cdot \pi \\ & = \pi \end{align*}\]

e a variância $Var(\hat{p}=\frac{1}{n}.\pi.(1-\pi)$):

\[\begin{align*} Var(\hat{p})& = Var(\frac{Y}{n}) \\ & = \frac{1}{n^{2}} \cdot Var(Y)\\ & = \frac{1}{n^{2}} \cdot n \cdot \pi \cdot (1-\pi)\\ & = \frac{1}{n} \cdot \pi \cdot (1-\pi ) \end{align*}\]

Assim, as proporções amostrais se distribuem de modo aproximadamente Normal sob uma média $\mu=\pi$ e com uma variância $\sigma^{2}=\frac{\pi \cdot (1- \pi)}{n}$:

\[ \hat{p} \sim N \left(\pi ; \frac{\pi \cdot (1- \pi) }{n} \right) \]

10.2.1 Simulações ilustrativas da aproximação da distribuição das proporções amostrais pela distribuição Normal

Para exemplificar considere o lançamento de um dado de seis faces,. A probabilidade de que uma certa face caia voltada para cima é de $\frac{1}{6}=0,167$. Se lançarmos esse dado um número crescente de vezes e anotarmos a proporção delas em que a face escolhida caiu voltada para cima comprova-se que o valor esperado das proporções amostrais aproxima-se da proporção populacional.

As Figuras 10.2 (tamanho de cada amostra $n=n_1$) e 10.3 (tamanho de cada amostra $n=n_2$) mostram o perfil assumido pela distribuição de 100 proporções amostrais obtidas de uma população que apresenta uma proporção $\pi=p_1$ da característica de interesse.

#############################################################################
# Considere uma população cuja característica de interesse (A) se manifesta de modo dicotômico:
# sim/não, sob uma probabilidade p_1 e (1-p_1).
# A probabilidade de se obter um elemento com a característica de interesse 
# - ao se sortear aleatoriamente um indivíduo qualquer - pode ser modelada como uma variável de Bernoulli.
# A probabilidade de se observar a característica de interesse ao se  
# repetir a amostragem (com reposição) por n_1 (n_2) vezes pode ser modelada como uma variável binomial (repetição de um experimento de Bernoulli n_1/n_2 vezes)   
# Repetindo-se esses experimentos binomiais por N vezes, as proporções amostrais de
# elementos com a característica de interesse (sucesso) nas N amostras obtidas será 
# dada pelo número de elementos de cada conjunto nas n_1 (n_2) repetições dividido por 
# n_1 (n_2).
# Desse modo, obtemos N proporções de amostras de tamanho n_1 (n_2)
#
#
# Selecionando-se aleatoriamente um elemento desta população 
# resulta em uma variável aleatória dicotômica/Bernoulli que assume 
# o valor 1 caso o elemento selecionado possua a propriedade A (sucesso)
# e assume o valor 0 caso não possua a propriedade A.
#
# A retirada (com reposição) de `n_1` elementos dessa população poderemos observar a frequência absoluta com que a propriedade A (sucesso) se manifesta na amostra, 
# a qual pode ser expressa  como uma variável aleatória (X) que segue o modelo teórico  Binomial de probabilidade. 
# 
# A frequência relativa, o quociente entre o número de sucessos por `n_1` expressa a 
# proporção com que a propriedade "A" foi observada na 'amostra' de tamanho `n_1` é também uma variável aleatória (p) com distribuição altamente relacionada à variável X  pois é a média de `n_1` ensaios (repetições) de Bernoulli.
#  
# Repetindo-se sucessivamente  `N` vezes extrações de tamanho `n_1` 
# a anotando-se a proporção de sucesso em cada uma dessas amostras poderemos analisar como eles se distribuem em relação à quantidade de elementos extraídos `n_1` (repetições de Bernoulli) 
# e à verdadeira proporção com que a propriedade A se manifesta na população (pi)  
#
# Demonstra-se que:
# para `n_1` suficientemente grande (repetições de Bernoulli com reposição);]
# n_1 * pi > 5 e 
# n_1*(1-pi) 5
# a distribuição de p pode ser aproximada pela distribuição Normal 
# tal que p ~N (mu,sigma)
# onde mu e sigma são aproximados por:
# mu = E(p) = pi
# sigma^2 = sigma^2*p >>>> sigma = sqrt[ p*(1-p)/(n_1)  ]
# 
#############################################################################

# Proporção escolhida para a manifestação da característica: sim/não (probabilidade de cada evento de Bernoulli)
p_1=round(1/6,2)

# Número de amostras
N=100             

# Tamanho escolhido para cada amostra: repetições de Bernoulli
n_1=10

# Vetor com o número de sucessos observados (a frequência absoluta) nas N amostras de n_1 elementos dicotômicos (repetições de Bernoulli, sob uma probabilidade individual de sucesso igual a p_1)

suc_10rep=rbinom(n=N, size = n_1, prob = p_1)
suc_10rep 

#  Vendo a proporção de sucessos (a frequência relativa) em cada uma das N_1 amostras de n_1 elementos dicotômicos
prop_10rep=suc_10rep/n_1
mean(prop_10rep) # ~ pi
sd(prop_10rep) # ~ sqrt(pi*(1-pi)/n_1)

# Dataframe com as N proporções amostrais sob n_1 
dados_10=as.data.frame(prop_10rep)

#############################################################################
# O mesmo procedimento, mas agora com amostras com um maior número de elementos em cada uma
#############################################################################

# Tamanho escolhido para cada amostra: repetições de Bernoulli
n_2=100

# Vetor com o número de sucessos observados (a frequência absoluta) nas N amostras de n_2 elementos dicotômicos (repetições de Bernoulli, sob uma probabilidade individual de sucesso igual a p_1)

suc_100rep=rbinom(n=N, size = n_2, prob = p_1)
suc_100rep 


#  Vendo a proporção de sucessos (a frequência relativa) em cada uma das N_1 amostras de n_1 elementos dicotômicos
prop_100rep=suc_100rep/n_2
mean(prop_100rep) # ~ pi
sd(prop_100rep) # ~ sqrt(pi*(1-pi)/n_2)

# Dataframe com as N proporções amostrais sob n_2 
dados_100=as.data.frame(prop_100rep)

meu_titulo1=paste("Distribuição de frequência das proporções de sucesso observadas em \n",N, "amostras de n=", n_1, "elementos dicotômicos extraídos (com reposição) da população","\n(proporção de sucesso na população \u03c0=", p_1,")")
meu_titulo2=paste("As proporções amostrais ~ \nN(\u03bc= \u03c0=",round(mean(dados_10$prop_10rep),3),";\u03c3 =sqrt(\u03c0*(1- \u03c0)/n)=",round(sd(dados_10$prop_10rep),3),")")


ggplot(dados_10, aes(x = prop_10rep)) + 
  geom_histogram(aes(y =..density..),
                 breaks = seq(0, 0.4, by = 0.05), 
                 colour = "black", 
                 fill = "lightblue") +
  stat_function(fun = dnorm, 
                args = list(mean = p_1, sd = sqrt(p_1*(1-p_1)/n_1)),
                 colour="red") +
  scale_y_continuous(name="",breaks = NULL) +
  scale_x_continuous(name="Valores das proporções amostrais") +
  #labs(title=meu_titulo1)+
  annotate(geom="text", x=mean(prop_10rep), y=max(dnorm(prop_10rep)),
           label=meu_titulo2, angle=0, vjust=0, hjust=0, color="blue",size=4)+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))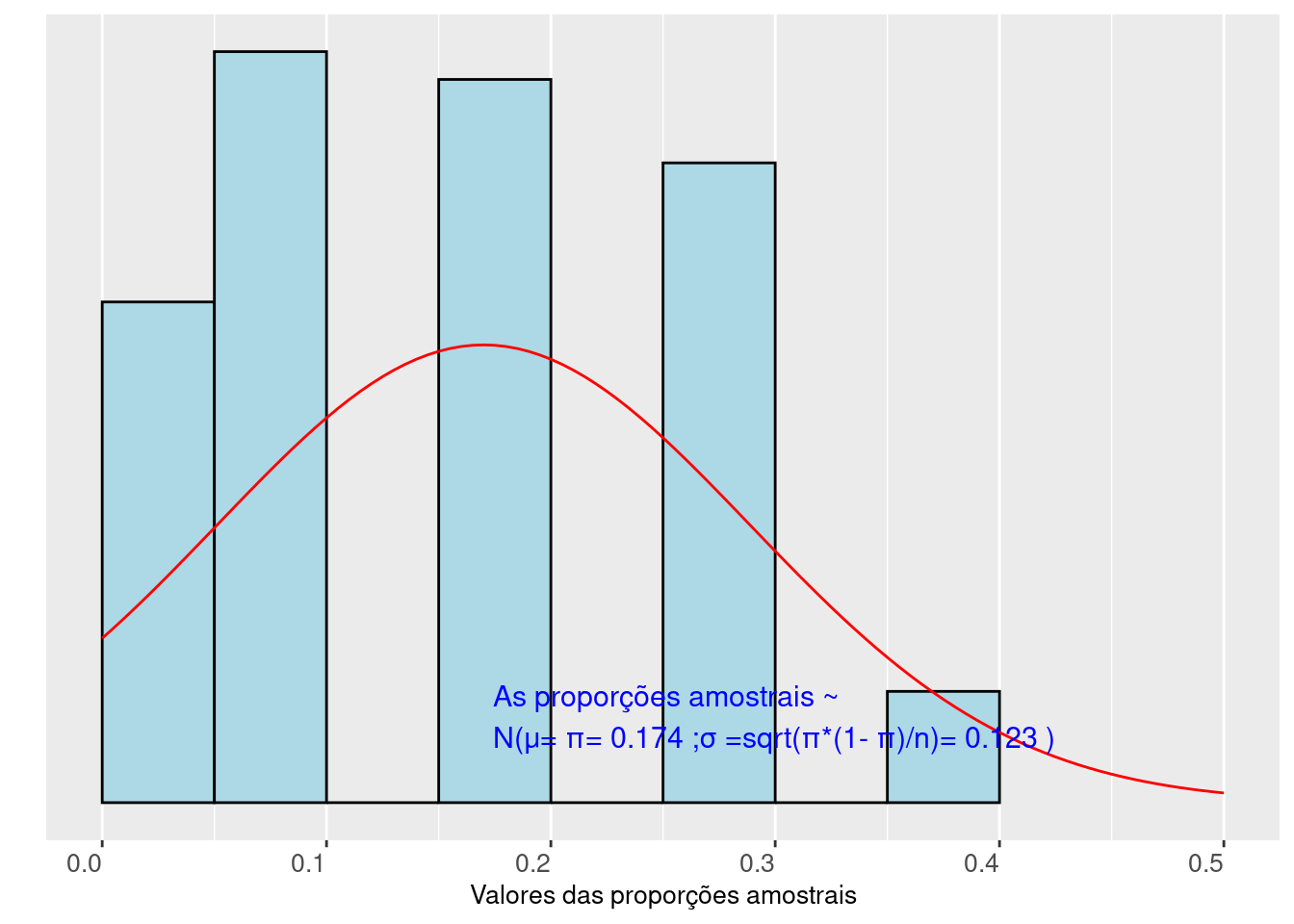

Distribuição das frequências das proporções de sucesso observadas em 100 amostras de tamanho n=10 elementos dicotômicos extraídos (com reposição) de uma população
(a proporção de sucesso na população é π=1/6)

Figure 10.2: Distribuição das frequências das proporções de sucesso observadas em 100 amostras de tamanho n=10 elementos dicotômicos extraídos (com reposição) de uma população
(a proporção de sucesso na população é π=1/6)

meu_titulo1=paste("Distribuição de frequências das proporções de sucesso observadas em \n",N, "amostras de n=", n_2, "elementos dicotômicos extraídos (com reposição) da população","\n(proporção de sucesso na população \u03c0=", p_1,")")
meu_titulo2=paste("As proporções amostrais ~ \nN(\u03bc= \u03c0=",round(mean(dados_100$prop_100rep),3),";\u03c3=sqrt(\u03c0*(1- \u03c0)/n)=",round(sd(dados_100$prop_100rep),3),")")

ggplot(dados_100, aes(x = prop_100rep)) + 
  geom_histogram(aes(y =..density..),
                 breaks = seq(0, 0.4, by = 0.03), 
                 colour = "black", 
                 fill = "lightblue") +
  stat_function(fun = dnorm, 
                args = list(mean = p_1, 
                            sd = sqrt(p_1*(1-p_1)/n_2)), 
                colour="red") +
  scale_y_continuous(name="",breaks = NULL) +
  scale_x_continuous(name="Valores das proporções amostrais") +
  #labs(title=meu_titulo1)+
  annotate(geom="text", x=mean(prop_100rep), y=max(dnorm(prop_100rep)),
           label=meu_titulo2, angle=0, vjust=0, hjust=0, color="blue",size=4)+
  theme(plot.title = element_text(size = 10, face = "bold"),
        axis.text.x = element_text(angle=0, hjust=1, size=10),
        axis.text.y = element_text(angle=0, hjust=1, size=10),
        axis.title.x = element_text(size = 10),
        axis.title.y = element_text(size = 10))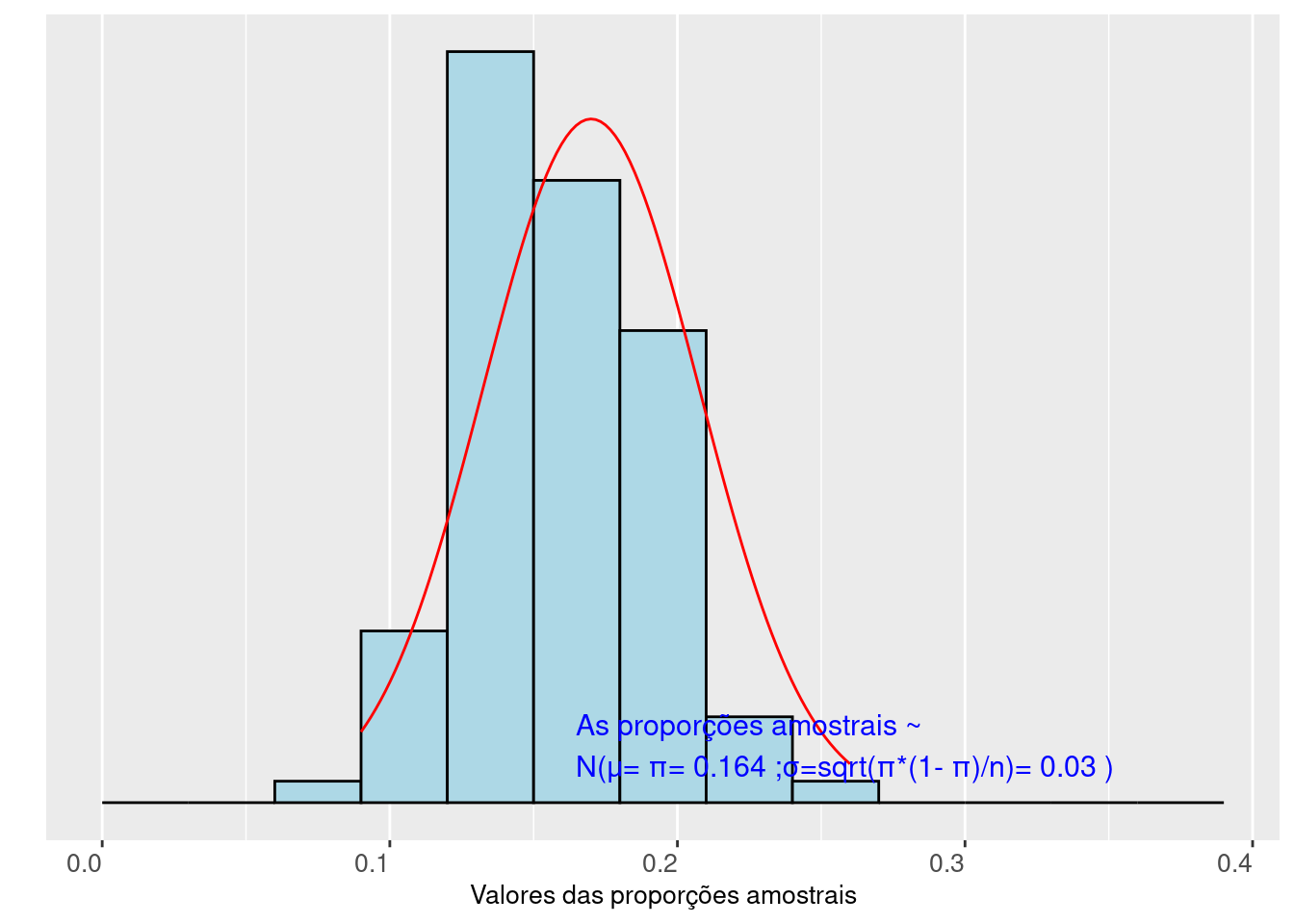

Distribuição das frequências das proporções de sucesso observadas em 100 amostras de tamanho n=100 elementos dicotômicos extraídos (com reposição) de uma população
(a proporção de sucesso na população é π=1/6)

Figure 10.3: Distribuição das frequências das proporções de sucesso observadas em 100 amostras de tamanho n=100 elementos dicotômicos extraídos (com reposição) de uma população (a proporção de sucesso na população é π=1/6)