4.7 Teorema de Bayes

Figure 4.20: Thomas Bayes (1702 - 1761)

Admita o espaço amostral de um experimento baseado no sorteio aleatório de um estudante de uma escola, com dois possíveis resultados quanto ao sexo:

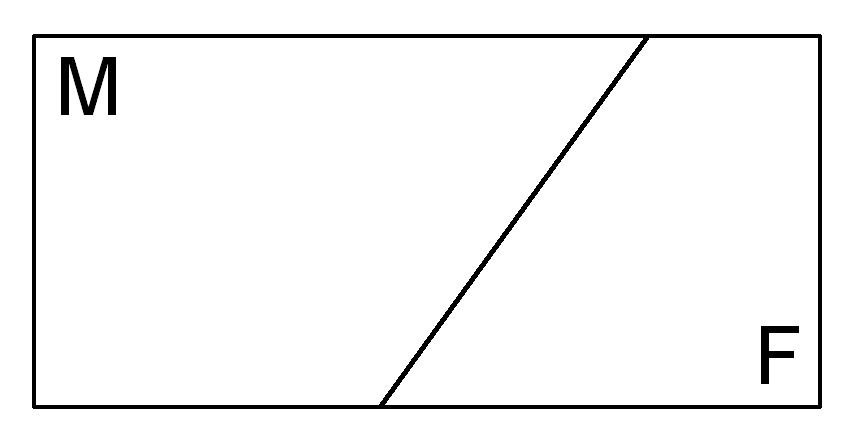
Figure 4.21: Espaço amostral

Considere agora um evento definido nesse espaço amostral como sendo ``ter um carro’’:

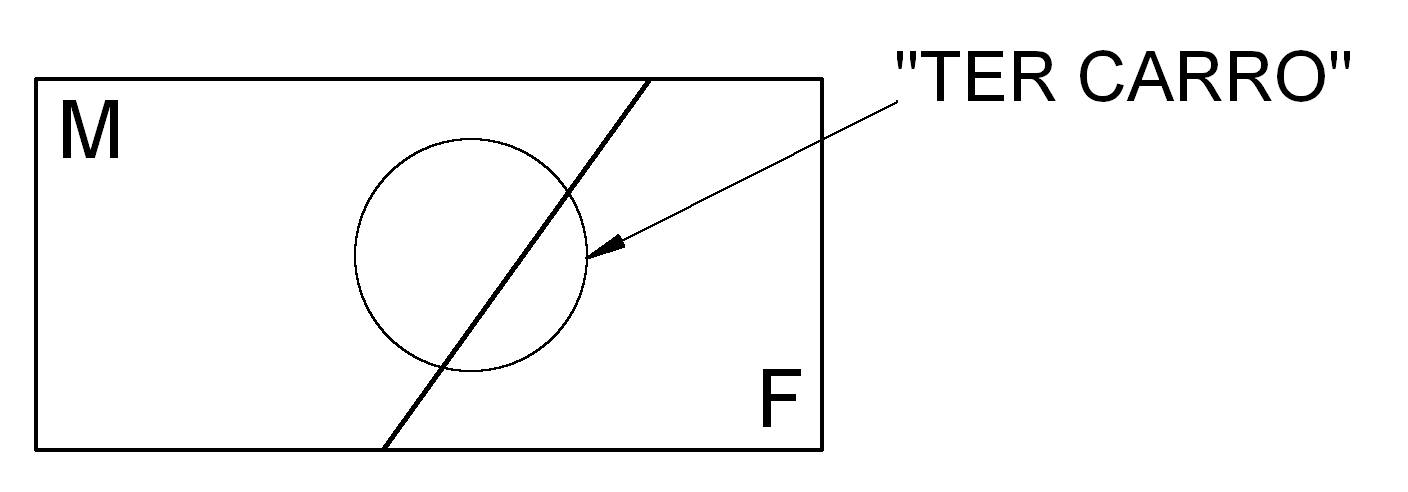
Figure 4.22: Espaço amostral

As interseções desse evento com os elementos do espaço amostral são:

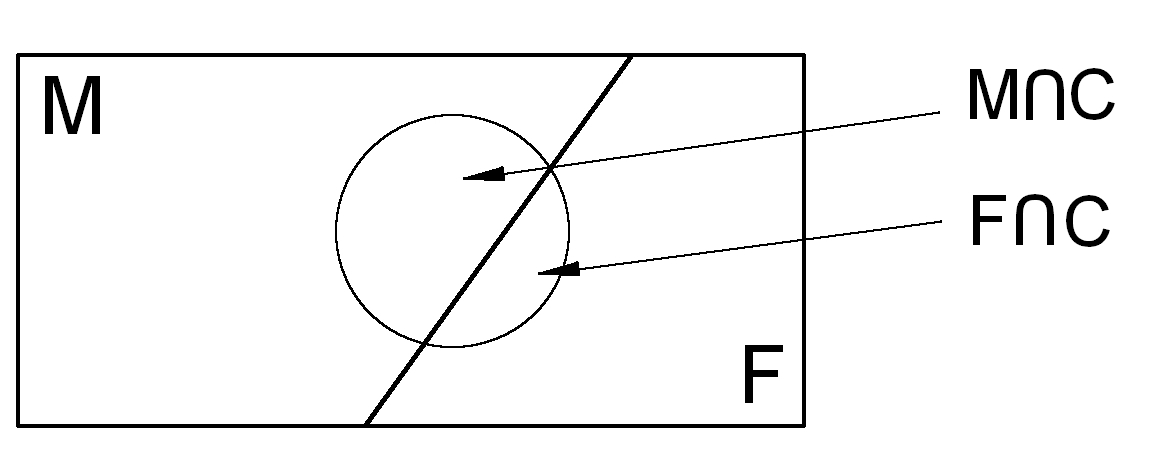
Figure 4.23: Espaço amostral

Pela regra da probabilidade condicionada temos que

\[ P(C|F) = \frac{P(C \cap F)}{ P(F)}\\ P(C \cap F) = P(C|F) P(F) \]

e, de modo equivalente,

\[ P(C|M) = \frac{P(C \cap M)}{ P(M)}\\ P(C \cap M) = P(C|M) P(M) \]

A probabilidade de se ter um carro é dada pela regra da união de eventos que, nesse caso são disjuntos e assim:

\[ P(C) = P(C \cap M) \cup P(C \cap F)\\ P(C) = P(C|M) P(M) + P(C|F) P(F) \]

Sorteado aleatoriamente um estudante da escola verificou-se possuir um carro. Qual a probabilidade de que seja do sexo feminino (\(P(F|C)\))?

\[ P(F|C) = \frac{P(F \cap C)}{ P(C)}\\ P(F \cap C) = P(F|C) P(C) \\ \]

Pela igualdade \(P(C \cap F)=P(F \cap C)\):

\[ P(C \cap F) = P(C|F) P(F) \\ P(F \cap C) = P(F|C) P(C) \]

substituindo-se na expressão acima chega-se a:

\[\begin{align*} P(C \cap F) & =P(F \cap C)\\ P(C|F).P(F) & = P(F|C).P(C)\\ P(F|C) & = \frac{P(C|F)P(F)}{P(C)} \end{align*}\]

uma relação entre duas probabilidades inversamente condicionadas conhecida como Teorema de Bayes.

Adimita então serem dados:

``M’’: ser do sexo masculino: \(P(M)=0,65\);
``F’’: ser do sexo feminino: \(P(F)=0,35\).
``C’’: possuir um carro:
- \(P(C|M)=0,30\)
- \(P(C|F)=0,18\).

A probabilidade de se ter carro (\(P(C)\)) resulta de união de dois únicos e possíveis eventos condicionados ao sexo e disjuntos. Assim:

\[\begin{align*} P(C) & = P(C \cap M) \cup P(C \cap F)\\ P(C) & = [P(M).P(C|M)] \cup [P(F).P(C|F)] \\ P(C) & = [0,65 . 0,30] + [0,35 . 0,18] \\ P(C) & = 0,258\\ \end{align*}\]

e podemos calcular \(P(F|C)\):

\[\begin{align*} P(F|C) & = \frac{P(F).P(C|F)}{P(C)}\\ P(F|C) & = \frac{0,35 . 0,18 }{ 0,258}\\ P(F|C) & = 0,2442\\ \end{align*}\]

A probabilidade de que um estudante aleatoriamente sorteado nessa escola e sabendo-se a priori que possui um carro ser do sexo feminino é de 24,42%.

Para um espaço amostral mais amplo, de modo geral consideremos, inicialmente o diagrama da Figura 4.24 onde \(\Omega\) é o espaço amostral de um experimento aleatório qualquer:

Figure 4.24: Espaço amostral

Admita que \(E_{1}\), \(E_{2}\), \(E_{3}\) e \(E_{4}\) formem a partição do espaço amostral \(\Omega\) (seus elementos são mutuamente exclusivos) como exposto na Figura 4.25

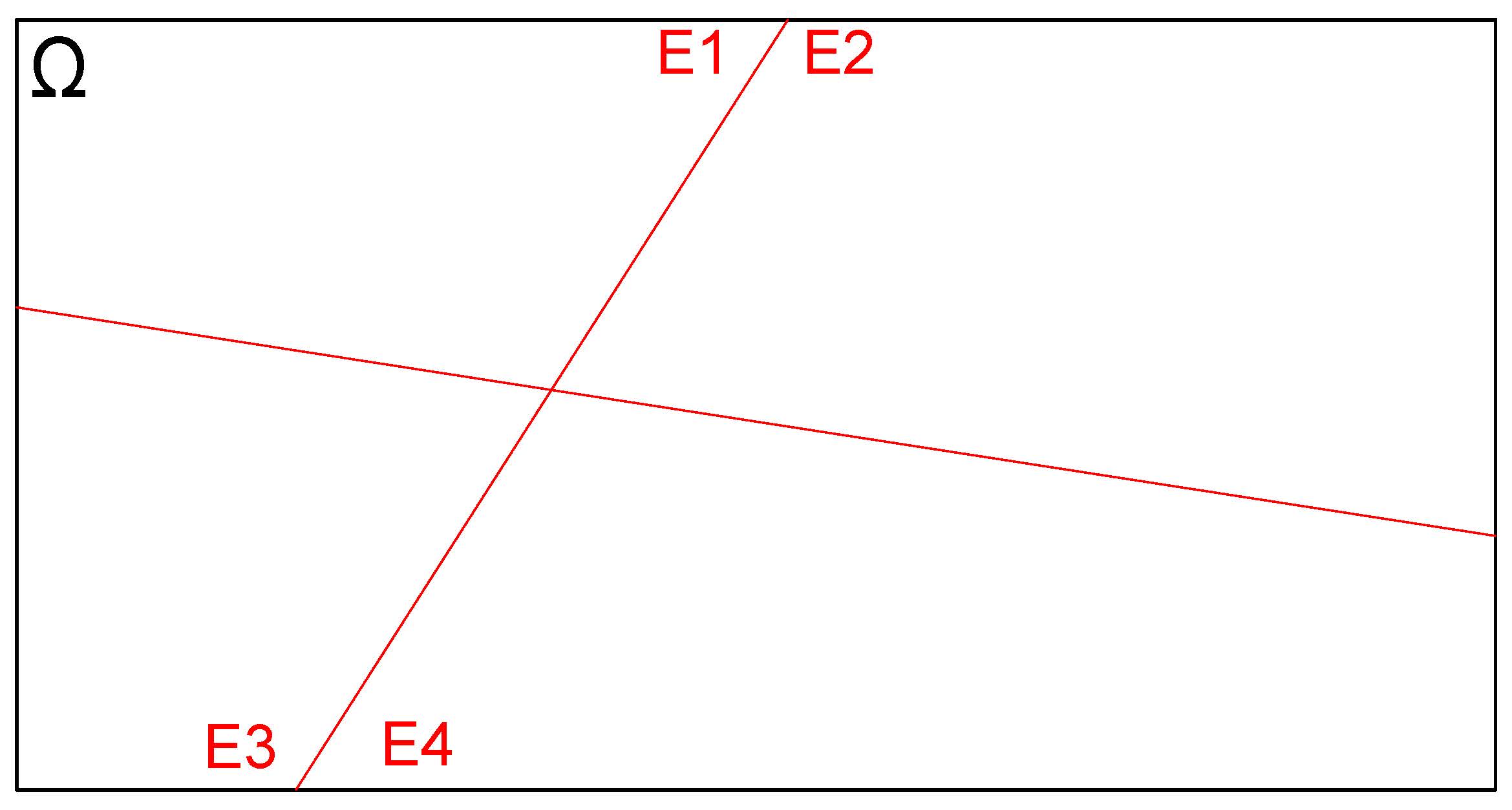
Figure 4.25: Espaço amostral e suas partições

E seja \(B\) um evento qualquer em \(\Omega\) como ilustrado na Figura 4.26

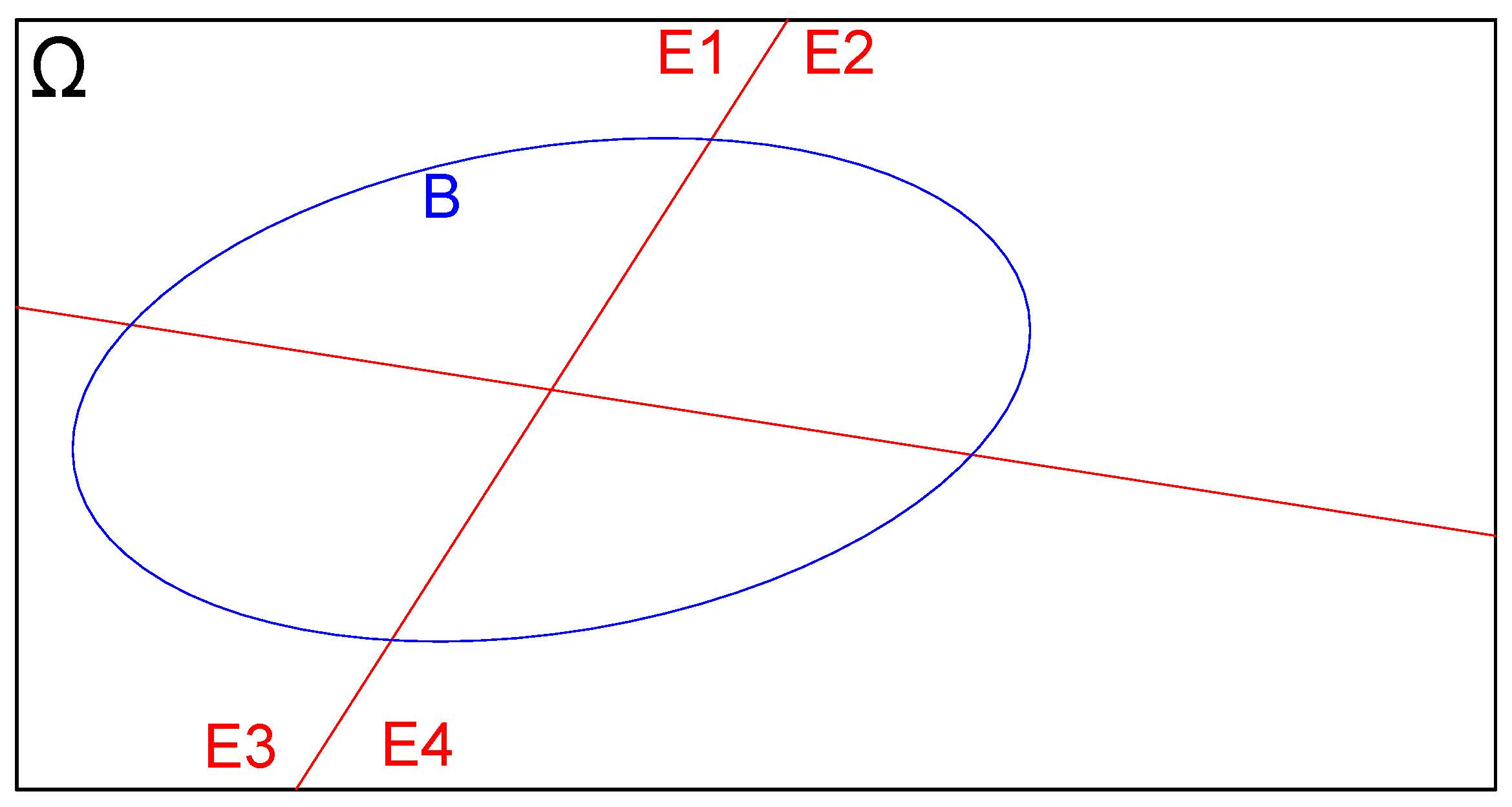
Figure 4.26: Evento definido sobre o espaço amostral

Delimitemos as interseções do evento \(B\) com as partições \(E_{1}\), \(E_{2}\), \(E_{3}\) e \(E_{4}\) do espaço amostral \(\Omega\), como ilustrado na Figura 4.27

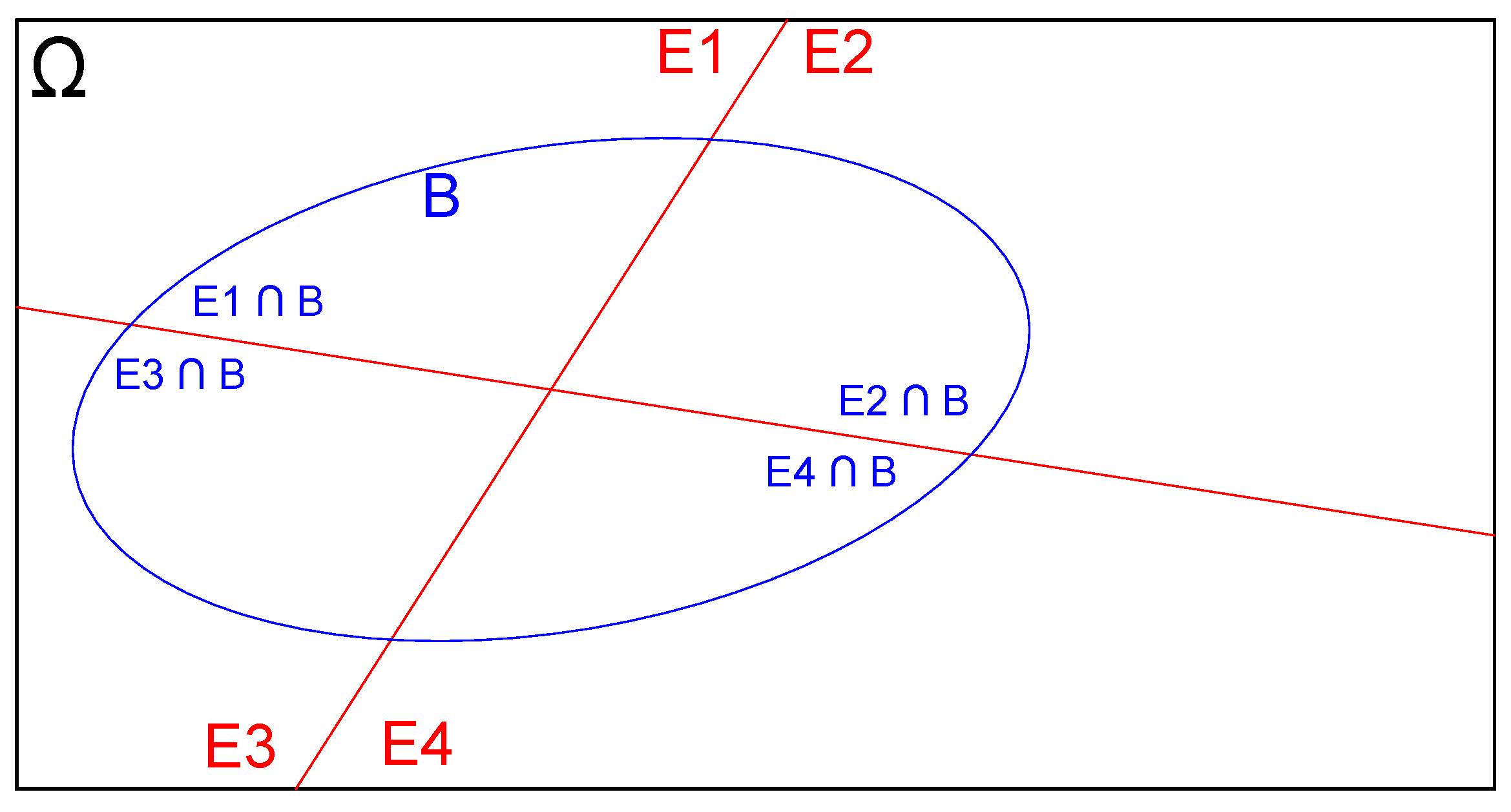
Figure 4.27: Interseções das partições do espaço amostral com o evento B

Isso pode ser estendido, em uma forma geral, para \(i=1, \dots, n\) partições como ilustrado na Figura 4.28

Figure 4.28: Interseções das n partições do espaço amostral com o evento B

Na representação esquemática da Figura 4.28 podemos identificar:

1- \(E_{1}\), \(E_{2}\), , \(E_{i}\), , \(E_{n}\) constituem-se em partições do espaço amostral \(\Omega\);
2- Todas as partições são mutuamente exclusivas: \(E_{i} \cap E_{j} = \varnothing\),\(\forall\) \(i \neq j\) (a interseção de quaisquer partições é vazia);
3- Sendo vazias as interseções entre quaisquer partições, o espaço amostral \(\Omega\) será a simples união de todas elas: \(\Omega = E_{1} \cup E_{2} \cup E_{3} \cup E_{4}\cup \dots \cup E_{i} \dots \cup E_{n}\); e,
4- B é um evento qualquer definido sobre as partições de \(\Omega\)

São conhecidas as probabilidades de ocorrência de cada um dos elementos do espaço amostral \(\Omega\):

\[ P(E_{1}); P(E_{2}); P(E_{3}); \dots;P(E_{i}); \dots; P(E_{n}) \]

e também as probabilidades do evento \(B\) condicionadas a cada elemento do espaço amostral:

\[ P(B|E_{1}); P(B|E_{2});\dots;P(B|E_{i});\dots; P(B|E_{n}) \]

A probabilidade de ocorrência do evento B é dada pela soma das probabilidades de cada uma de suas interseções com os elementos do espaço amostral \(\Omega\), uma vez que essas interseções são disjuntas entre si:

\[\begin{align*} P(B) & = P(E_{1} \cap B) \cup P(E_{2} \cap B) \cup \dots P(E_{i} \cap B) \cup \dots P(E_{n} \cap B) \\ P(B) & = \sum _{i=1}^{n}P\left({E}_{i}\cap B\right) \end{align*}\]

Pela Regra do produto de eventos condicionados, a probabilidade de ocorrência do evento B posto ter ocorrido um evento \(E_{i}\) é:

\[\begin{align*} P(B|E_{i}) & = \frac{P(E_{i}\cap B)}{P(E_{i})} \\ P(E_{i}\cap B) & = P(E_{i}) \times P(B|E_{i}) \end{align*}\]

com \(P(E) > 0\)

Aplicando-se na expressão anteriormente desenvolvida da probabilidade de ocorrência do evento B teremos:

\[\begin{align*} P(B) & = P(E_{1} \cap B) \cup P(E_{2} \cap B) \cup \dots \cup P(E_{i} \cap B) \cup \dots \cup P(E_{n} \cap B) \\ P(B) & = P(E_{1}) \times P(B|E_{1}) + P(E_{2}) \times P(B|E_{2}) + \\ & \dots +P(E_{i}) \times P(B|E_{i}) + \\ & \dots + P(E_{n}) \times P(B|E_{n}) \end{align*}\]

Portanto a probabilidade total do evento B em \(\Omega\) é dada pelo somatório:

\[ P(B) = \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\cdot P\left(B|{E}_{i}\right)\right] \]

Pela Regra do produto de eventos condicionados a probabilidade de ocorrência de um evento \(E_{i}\) posto ter ocorrido o evento \(B\) é:

\[\begin{align*} P(E_{i}|B) & = \frac{P(E_{i} \cap B)}{P(B)} \\ P(E_{i} \cap B) & = P(B) \times P(E_{k}|B) \\ P(B) & = \frac{P(E_{i}\cap B)}{P(E_{k}|B)} \end{align*}\]

com \(P(B) > 0\)

Pela igualdade dos dois modos de se expressar a probabilidade total do evento \(B\) desenvolvidos:

\[ P(B) = \frac{P(E_{i}\cap B)}{P(E_{i}|B)} \]

\[ P(B) = \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\cdot P\left(B|{E}_{i}\right)\right] \]

tem-se

\[ \frac{P(E_{i}\cap B)}{P(E_{i}|B)}=\sum _{i=1}^{n}\left[P\left({E}_{i}\right)\cdot P\left(B|{E}_{i}\right)\right] \]

Rearranjando-se em termos da expressão anterior para exprimir a probabilidade de ocorrência de um evento \(E_{i}\) posto ter ocorrido o evento \(B\) chegamos a:

\[ P(E_{i}|B) = \frac{P(E_{i}\cap B)}{\sum _{i=1}^{n}\left[P\left({E}_{i}\right)\cdot P\left(B|{E}_{i}\right)\right]} \]

Sendo

\[ P(E_{i} \cap B) = P(B) \times P(E_{i}|B) \]

a expressão anterior pode ser reescrita como:

\[ P(E_{i}|B) = \frac{ P(E_{i}) \times P(B|E{i}) }{ \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \]

uma forma mais geral do Teorema de Bayes.

O Teorema de Bayes é também chamado de Teorema da probabilidade a posteriori ao permitir que se calcule \(P(E_{i}|B)\) em termos da ocorrência \(P(B|E_{i})\)

É, de certo modo, uma conjugação do teorema na probabilidade total e da regra do produto de probabilidades.

O denominador:

\[ P(B)= \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] \]

é a denominada probabilidade marginal de ocorrência do evento \(B\) no espaço amostral \(\Omega\) composto por \(n\) elementos (partições).

Na expressão do Teorema de Bayes:

\(P(E_{k}|B)\) é a denominada probabilidade a posteriori do evento \(E_{k}\) condicionada pela ocorrência anterior do evento B;
\(P(E_{k})\) é a denominada probabilidade a priori do evento \(E_{k}\);
\(P(B|E_{k})\) é a denominada probabilidade a posteriori do evento \(B\) condicionada pela ocorrência anterior do evento \(E_{k}\);
\(P(E_{i})\) é a denominada probabilidade a priori de cada evento \(E_{i}\);
\(P(B|E_{i})\) é a denominada probabilidade a posteriori do evento \(B\) condicionada pela ocorrência anterior de cada evento \(E_{i}\).

Exemplo: Constatou-se que o aumento nas vendas de um certo produto comercializado por uma empresa num mês pode ocorrer somente por uma das quatro causas mutuamente exclusivas a seguir:

1- ação de marketing;
2- propaganda;
3- flutuações na economia do país; ou,
4- efeitos sazonais.

A probabilidade de haver uma ação da empresa no mês focada para o marketing é de 40%; e para propaganda é de 30%; as probabilidades de ocorrerem flutuações na economia do país é de 20% e de efeitos sazonais é de 10%. Uma pesquisa mostrou que a probabilidade de haver um aumento nas vendas do produto devido a uma ação de marketing é de 7%; devido à publicidade, de 7,5%, por flutuações na economia do país, de 3% e por sazonalidade de 2%.

Em um determinado mês a empresa observou um considerável incremento nas vendas. Qual seria sua causa mais provável? Qual a probabilidade de incremento das vendas em um certo mês?

Inicialmente definimos um experimento aleatório como sendo “qual fato ocorreu no mês”.

Não sabemos qual fato ocorreu, mas sabemos que as possibilidades são apenas 4 (marketing, propaganda, flutuações na economia ou efeitos sazonais).

Podemos então conceber que esses fatos são elementos do espaço amostral do experimento aleatório: pois são eventos exaustivos e exclusivos: não pode ocorrer mais de um ao mesmo tempo e ao menos um ocorrerá.

Assim esse espaço amostral é composto pelos seguintes “elementos” e suas probabilidaes são tiradas do enunciado:

\(E_{1}\) o elemento “Ação de marketing” \(\therefore \rightarrow\) \(P(E_{1})=0,40\);
\(E_{2}\) o elemento “Ação de propaganda” \(\therefore \rightarrow\) \(P(E_{2})=0,30\);
\(E_{3}\) o elemento “Flutuações na economia” \(\therefore \rightarrow\) \(P(E_{3})=0,20\); ou,
\(E_{4}\) o elemento “Sazonalidade” \(\therefore \rightarrow\) \(P(E_{4})=0,10\).

Chamemos de \(B\) ao evento “ocorrer um incremento nas vendas”, um evento construído sobre os elementos do espeço amostral e que apresenta diferentes probabilidades a depender de qual elemento do espaço amostral ocorreu (a probabilidade de \(B\) está condicionada aos elementos do espaço amstral). Da leitura do enunciado extraímos as probabilidades de ocorrência de cada um dos eventos influenciadores:

As probabilidades condicionadas de ocorrer um incremento das vendas (\(B\)) pela ocorrência anterior de cada um dos elementos do espaço amostral (posto ter ocorrido o evento \(E_{i}\)) também são tiradas do enunciado:

\(P(B|E_{1}) = 0,07\) ;
\(P(B|E_{2}) = 0,075\);
\(P(B|E_{3}) = 0,03\); e,
\(P(B|E_{4}) = 0,02\).

Para responder à indagação do problema (“Qual a causa mais provável?”) podemos invertê-la e reformulá-la:

“Qual a probabilidade de ter ocorrido cada um dos quatro eventos (\(E_{1}\), \(E_{2}\), \(E_{3}\), \(E_{4}\)) posto (dado) ter ocorrido um incremento nas vendas?

Calculemos para cada um deles usando o Teorema de Bayes:

\[ P(E_{i}|B) = \frac{ P(E_{i}) \times P(B|E{i}) }{ \sum _{i=1}^{n}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \]

Probabilidade da empresa ter realizado uma ação de marketing, posto ter ocorrido um incremento nas vendas de seu produto:

\[\begin{align*} P(E_{1}|B) & = \frac{ P(E_{1}) \times P(B|E{1}) }{ \sum _{i=1}^{4}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \\ P(E_{1}|B) & = \frac{0,40 \times 0,07} { (0,40 \times 0,07) + (0,30 \times 0,075) +(0,20 \times 0,03) +(0,10 \times 0,02) } \\ P(E_{1}|B) & = 0,4786 \\ \end{align*}\]

Probabilidade da empresa ter realizado propaganda, posto ter ocorrido um incremento nas vendas de seu produto:

\[\begin{align*} P(E_{2}|B) & = \frac{ P(E_{2}) \times P(B|E{2}) }{ \sum _{i=1}^{4}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \\ P(E_{2}|B) & = \frac{0,30 \times 0,075} { (0,40 \times 0,07) + (0,30 \times 0,075) +(0,20 \times 0,03) +(0,10 \times 0,02) } \\ P(E_{2}|B) & = 0,3846 \end{align*}\]

Probabilidade da empresa ter ocorrido flutuações na economia, posto ter ocorrido um incremento nas vendas de seu produto:

\[\begin{align*} P(E_{3}|B) & = \frac{ P(E_{3}) \times P(B|E{3}) }{ \sum _{i=1}^{4}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \\ P(E_{3}|B) & = \frac{0,20 \times 0,03} { (0,40 \times 0,07) + (0,30 \times 0,075) +(0,20 \times 0,03) +(0,10 \times 0,02) } \\ P(E_{3}|B) & = 0,1026 \end{align*}\]

Probabilidade da empresa ter ocorrido efeitos sazonais, posto ter ocorrido um incremento nas vendas de seu produto:

\[\begin{align*} P(E_{4}|B) & = \frac{ P(E_{4}) \times P(B|E{4}) }{ \sum _{i=1}^{4}\left[P\left({E}_{i}\right)\times P\left(B|{E}_{i}\right)\right] } \\ P(E_{4}|B) & = \frac{0,10 \times 0,02} { (0,40 \times 0,07) + (0,30 \times 0,075) +(0,20 \times 0,03) +(0,10 \times 0,02) } \\ P(E_{4}|B) & = 0,03419 \end{align*}\]

Respostas:

1- Os cálculos indicam que o evento mais provável pelo incremento das vendas observado naquele mês foi o de uma ação de marketing;
2- A probabilidade de incremento das vendas em um determinado mês como resultado dos quatro possíveis eventos indicados é o próprio denominador do Teorema de Bayes: 0,0585.

Exemplo: Considere 5 urnas, cada uma delas contendo 6 bolas. Duas dessas urnas (urnas tipo \(C_{1}\)) possuem 3 bolas brancas em seu interior. Duas outras (urnas tipo \(C_{2}\)) possuem 2 bolas brancas em seu interior e a última (urnas tipo \(C_{3}\)) possui 6 bolas brancas em seu interior (cf. Figura 4.29).

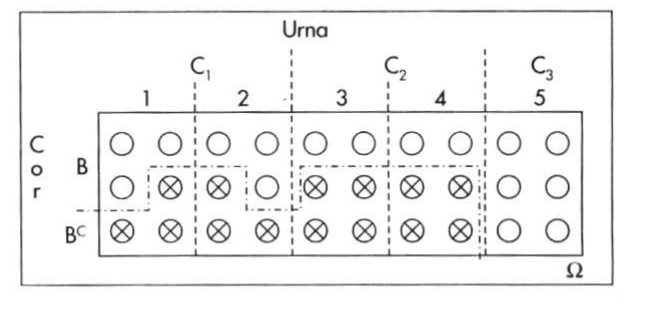
Figure 4.29: Cinco urnas cada uma com 6 bolas em cores de diferentes quantidades da cor branca

Escolhida aleatoriamente uma urna retira-se uma bola. Qual a probabilidade da urna escolhida ter sido a urna \(C_{3}\) sabendo-se que a bola retirada foi branca?

Desejamos determinar \(P(C_{3} | Branca)\)

Da leitura do enunciado extraímos as seguintes informações:

\[\begin{align*} P(C_{1}) & = \frac{2}{5} \\ P(C_{2}) & = \frac{2}{5} \\ P(C_{3}) & = \frac{1}{5} \\ P(Branca | C_{1}) & = \frac{1}{2} \\ P(Branca | C_{2}) & = \frac{1}{3} \\ P(Branca | C_{3}) & = 1 \end{align*}\]

\[\begin{align*} P(C_{3} | Branca) & = \frac{ P(C_{3}) \times P(Branca | C_{3}) }{ \sum_{i=1}^{3}\left[P\left({C}_{i}\right)\times P\left(Branca | {C}_{i}\right)\right] } \\ P(C_{3} | Branca) & = \frac{ 0,20 \times 1,00} { (0,40 \times 0,50 ) + (0,40 \times 0,33 ) +(0,20 \times 1,00)} \\ P(C_{3} | Branca) & = 0,375 \end{align*}\]