10.5 Intervalos de confiança para proporções amostrais

Podemos escrever o parâmetro (\(\pi\)) da proporção populacional em função da proporção amostral observada \(\hat{p}\) e de seu desvio padrão \(\sigma_{\hat{p}}\):

\[ Z=\frac{\hat{p}-\pi }{\sqrt{\frac{\pi \left(1-\pi \right)}{n}}} \sim N\left(0,1\right), \]

ou

\[ Z=\frac{\hat{p}-\pi }{{\sigma }_{\hat{p}}} \]

com \(Z \sim N\left(0,1\right)\).

Assim,

\[ \hat{p} - \pi = Z \cdot {\sigma }_{\hat{p}} \]

e

\[ \pi = \hat{p} + Z \cdot {\sigma }_{\hat{p}} \]

Observa-se, todavia, que a variância da distribuição Normal da aproximação da distribuição das proporções amostrais é expressa em termos do parâmetro da proporção populacional \(\pi\) que não é conhecido:

\[ \hat{p} \sim N [\pi ; \frac{\pi \cdot (1- \pi) }{n} ] \]

\[ {\sigma }_{\hat{p}}=\sqrt{\frac{\pi \left(1-\pi \right)}{n}}. \]

Demonstra-se que para:

• um razoável número de repetições: \(n \ge 30\);
  
• de uma população onde a proporção \(\pi\) não é extrema: próximas a 0 ou 1; e tal que
• \((n \cdot \pi)\) e \((n \cdot (1-\pi))\) sejam maiores que 15 (alguns autores consideram limites mais brandos, iguais a 10 ou ainda a 5),

Podemos tomar a proporção amostral \(\hat{p}\) como uma aproximação direta da proporção populacional \(\pi\) na expressão da variância da distribuição Normal que modela a distribuição das proporções amostrais sem que isso resulte em grande alteração na distribuição da variável \(Z\).

Ou ainda, alternativamente, fazendo-se antes uma aproximação com correção de continuidade, onde definimos uma nova estimativa amostral da proporção populacional \(\hat{p}_{c}\) corrigida:

\[ \hat{p}_{c} = \hat{p}+\frac{1}{2n} \]

se \(\hat{p} < 0,50\),

ou

\[ \hat{p}_{c} = \hat{p}- \frac{1}{2n} \]

se \(\hat{p} > 0,50\).

As probabilidades associadas aos valores assumidos pela variável \(Z \sim N\left(0,1\right)\): a área sob a curva, encontram-se tabelados e podem ser utilizados para construir intervalos de confiança para o parâmetro da proporção populacional \(\pi\) associados a probabilidades desejadas.

\[ P [ \hat{p} - Z \cdot {\sigma }_{\hat{p}} < \pi < \hat{p} + Z \cdot {\sigma }_{\hat{p}} ] = (1-\alpha) \]

Assim (com \(\hat{p}\) ou \(\hat{p}_{c}\)) podemos construir intervalos de confiança em torno da proporção populacional \(\pi\) associados a um nível de significância estabelecido:

Bilaterais: intervalo delimitado por dois valores: mínimo e máximo, para a proporção amostral, dentro do qual todos os valores possuem um mesmo nível de significância:

\[ P[\hat{p} - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} \hspace{0.1cm} \le \hspace{0.1cm} \pi \hspace{0.1cm} \le \hspace{0.1cm} \hat{p} + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1-\hat{p} \right)}{n}}] = (1-\alpha) \]

Unilaterais: intervalos delimitados apenas em um de seus lados nos quais todos os valores possuem um mesmo nível de significância:

• Valor máximo (limitando à direita):

\[ P[\pi \le \hat{p} + {z}_{\alpha} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} ] = (1- \alpha) \]

• Valor mínimo (limitando à esquerda):

\[ P [\pi \hspace{0.1cm} \ge \hat{p} - {z}_{\alpha} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} \hspace{0.1cm}] = (1-\alpha) \]

# Intervalos de confiança das proporções amostrais observadas

IC.N = function (N, n, p, conf, er) {
zc = qnorm(1-((1-conf)/2)) #Z=1,96  
suc=rbinom(n=N, size = n, prob = p)
prop_suc=suc/n
dados=as.data.frame(prop_suc)
dados$lim_sup=dados$prop_suc + zc*sqrt(dados$prop_suc*(1-dados$prop_suc)*(1/n))         
dados$lim_inf=dados$prop_suc - zc*sqrt(dados$prop_suc*(1-dados$prop_suc)*(1/n))   
names=c("Proporção amostral", "lim superior", "lim inferior")
colnames(dados)=names
row.names(dados)=NULL
meu_titulo001=paste0("Intervalos com iguais níveis de confiança fixados em ", 100*conf, "% \n(",N," amostras de tamanho ",n,") \nAs linhas verticais mostram a propoção populacional em azul (\u03c0: ", p , ") \ne a média das proporções amostrais em vermelho ( \u0070\u0302: ",round(mean(dados$`Proporção amostral`),4) , ").")
meu_titulo002=paste0("Parâmetros da distribuição da população Normal aproximada ( \u03bc, \u03c3) = (", round(mean(dados$`Proporção amostral`),4) ,", ", round(sqrt(p*(1-p)/n),4)     ,")")  



plot(0, 0, 
type="n", 
xlim=c( 0.5*min(dados$`lim inferior`) , 1.1*max(dados$`lim superior`) ), 
ylim=c(0,N), 
bty="l",
xlab="Proporções amostrais observadas", 
ylab="Amostras extraídas", 
main="", #meu_titulo001
sub="") #meu_titulo002

for (i in 1:N) {
prop_amostral=dados$`Proporção amostral`[i]
li = dados$`lim inferior`[i]
ls = dados$`lim superior`[i]
plotx = c(li,ls)
ploty = c(i,i)
if (li > p | ls < p) lines(plotx,ploty, col="red", lwd=2, lend=0)
  else lines(plotx,ploty, lend=0) 
    if (li > p | ls < p) points(prop_amostral, i, col="red", cex=1)+text(y=i+3,x=prop_amostral, labels=round(prop_amostral,1), cex=1, col='red')
      else points(prop_amostral, i, col="black", cex=1) 
segments(x0=mean(dados$`Proporção amostral`) , y0=0, x1=mean(dados$`Proporção amostral`) ,y1=N,col="red", lwd=2, lty=2)
segments(x0=p , y0=0, x1=p ,y1=N,col="blue", lwd=2, lty=1)
} 
}

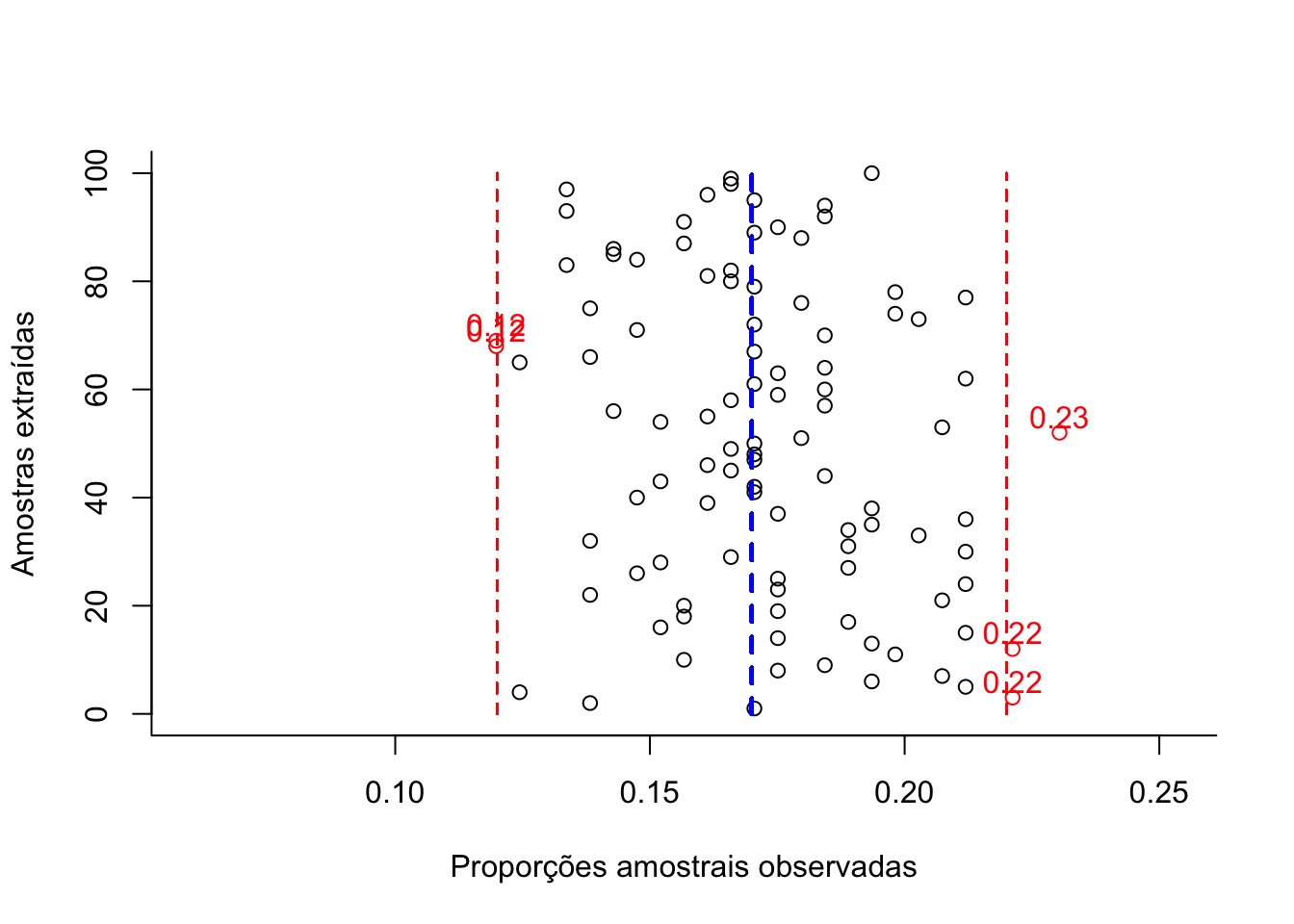
Figure 10.8: Intervalos de confiança construídos para as diversas proporções amostrais obtidas de amostragens (com reposição) de elementos de uma população que apresentam a característica de interesse se manifestando de modo dicotômico. O dimensionamento foi estimado ignorando-se o conhecimento da proporção populacional (π) para um nível de confiança (1-α) e um erro amostral (ε) estipulados: 385 elementos.

Exemplo: Em uma amostra aleatória, 136 pessoas de um grupo de 400 que receberam a vacina contra gripe, declararam haver sentido algum efeito colateral. Construa um intervalo com 95% de confiança para a verdadeira proporção populacional da ocorrência de efeitos colaterais vacinais .

Dados do problema:

• \(\hat{p}=\frac{136}{400}=0,34\) é a proporção amostral observada;
• o tamanho amostral (\(n=400\)) é grande e a proporção amostral (\(\hat{p}=0,34\)) não é extrema (próxima a zero ou um);
  
• \(\pi\) é a proporção populacional (desconhecida); e,
• para o nível de confiança solicitado (\((1-\alpha)=0,95\)) temos da tabela \({z}_{\left(\frac{\alpha }{2}\right)}= +/-1,96\).

Um intervalo bilateral (fechado) para a proporção populacional desconhecida (\(\pi\)) sob um nível de confiança (\(1-\alpha\)) de 0,95 estará delimitado:

\[\begin{align*} \hat{p} - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} \le & \pi \le \hat{p} + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1-\hat{p} \right)}{n}}\\ 0,34 - 1,96 \cdot \sqrt{ \frac{0,34 \cdot (1-0,34)}{400} } \le & \pi \le 0,34 + 1,96 \cdot \sqrt{ \frac{0,34 \cdot (1-0,34)}{n} }\\ 0,2936\le & \pi \le 0,3864 \end{align*}\]

Exemplo: Em uma amostra aleatória de 2000 eleitores do Brasil constatou-se uma intenção de voto de 43% para um candidato à presidência. Realizada a eleição, deseja-se inferir qual o intervalo de variação da proporção populacional a um nível de confiança de 99%.

Dados do problema:

• \(\hat{p}=0,43\) é a proporção amostral observada;
• o tamanho amostral (\(n=2000\)) é grande e a proporção amostral (\(\hat{p}=0,43\)) não é extrema (próxima a zero ou um);
  
• \(\pi\) é a proporção populacional (desconhecida); e,
• para o nível de confiança solicitado (\((1-\alpha)=0,99\)) temos da tabela \({z}_{\left(\frac{\alpha }{2}\right)}= +/-2,58\).

Um intervalo bilateral (fechado) para a proporção populacional desconhecida (\(\pi\)) sob um nível de confiança (\(1-\alpha\)) de 0,99 estará delimitado:

\[\begin{align*} \hat{p} - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1- \hat{p} \right)}{n}} \le & \pi \le \hat{p} + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{\frac{\hat{p} \cdot \left(1-\hat{p} \right)}{n}}\\ 0,43 - 2,58 \cdot \sqrt{ \frac{0,43 \cdot (1-0,43)}{2000} } \le & \pi \le 0,43 + 2,58 \cdot \sqrt{ \frac{0,43 \cdot (1-0,43)}{2000} }\\ 0,4014\le & \pi \le 0,4586\\ \end{align*}\]

10.5.1 Intervalos de confiança para a diferença entre duas proporções amostrais

Para a construção de um intervalo de confiança para a diferença de duas proporções populacionais \(\pi_{X}\) e \(\pi_{Y}\) a partir das proporções obtidas em duas amostras de razoável tamanho (\(n_{X} \ge 30\) e \(n_{Y} \ge 30\)) e proporções amostrais \(\hat{p}_{X}\) e \(\hat{p}_{Y}\) não extremas (próximos a zero ou um) demosntra-se que a variável aleatória dessa diferença é tal que

\[ Z=\frac{(\hat{p}_{X}-\hat{p}_{Y} )- (\pi_{X}-\pi_{Y}) }{\sqrt{ \frac{\pi_{X}(1-\pi_{X})}{n_{X}}+ \frac{\pi_{Y}(1-\pi_{Y})}{n_{Y}}}} \sim N\left(0,1\right), \]

Sob as condições anunciadas, demostran-se que se pode tomar as proporções amostrais \(\hat{p}_{X}\) e \(\hat{p}_{Y}\) como aproximações diretas das proporções populacionais \(\pi_{X}\) e \(\pi_{Y}\) na expressão da variância da distribuição Normal que modela a distribuição das diferenças das proporções amostrais sem que isso resulte em grande alteração na distribuição da variável \(Z\).

\[ Z=\frac{(\hat{p}_{X}-\hat{p}_{Y} )- (\pi_{X}-\pi_{Y}) }{\sqrt{ \frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}} \sim N\left(0,1\right), \]

Assim podemos construir intervalos de confiança em torno da diferença das proporções populacionais \(\pi_{X}\) e \(\pi_{Y}\) associados a um nível de significância estabelecido:

Bilaterais: intervalo delimitado por dois valores: mínimo e máximo, para a proporção amostral, dentro do qual todos os valores possuem um mesmo nível de significância:

\[ P\left[(\hat{p}_{X}-\hat{p}_{Y}) - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{{\frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}} \\ \le \hspace{0.1cm} (\pi_{X}-\pi_{Y}) \hspace{0.1cm} \le \hspace{0.1cm} \\ (\hat{p}_{X}-\hat{p}_{Y}) + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{{\frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}}\right] = (1-\alpha) \]

Unilaterais: intervalos delimitados apenas em um de seus lados nos quais todos os valores possuem um mesmo nível de significância:

• Valor máximo (limitando à direita):

\[ P\left[(\pi_{X}-\pi_{Y}) \hspace{0.1cm} \le \hspace{0.1cm} (\hat{p}_{X}-\hat{p}_{Y}) + {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{{\frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}}\right] = (1-\alpha) \]

• Valor mínimo (limitando à esquerda):

\[ P\left[(\pi_{X}-\pi_{Y}) \hspace{0.1cm} \ge \hspace{0.1cm} (\hat{p}_{X}-\hat{p}_{Y}) - {z}_{\left(\frac{\alpha }{2}\right)} \cdot \sqrt{{\frac{\hat{p}_{X}(1-\hat{p}_{X})}{n_{X}}+ \frac{\hat{p}_{Y}(1-\hat{p}_{Y})}{n_{Y}}}}\right] = (1-\alpha) \]