3.3 Sínteses numéricas descritivas


Além da apresentação elementar de algumas informações relacionadas aos dados brutos da amostra, tais como os valores mínimo e máximo observados, a estatística descritiva possui muitas outras ferramentas para condensar a informação contida nos dados.


São chamadas de sínteses numéricas, medidas que condensam variados aspectos relacionados aos valores dos dados. As principais sínteses numéricas são:


  • de tendência central (posição): média (simples ou aritmética, geométrica, harmônica, anarmônica, quadrática, biquadrática), moda e mediana;
  • de dispersão (variabilidade): absolutas (amplitude total, variância e desvio padrão) ou relativas (coeficiente de variação, unidades padronizadas); e,
  • de subdivisão (separatrizes, quantis): mediana (50%), quartis (25%, 50%, 75%), decis (10%, ….90%) e percentis (1%….99%).


Uma medida de posição ou dispersão é dita resistente quando forem pouco afetadas pela alteração de uma pequena porção dos dados. A mediana é uma medida resistente, já a média e a variância não são.

3.3.1 Medidas de tendência central (posição)

3.3.1.1 Média


Sejam \(x_{1}, x_{2}, ..., x_{n}\) os \(n\) valores assumidos pela variável \(X\) (dados brutos). A média aritmética simples será dada por:


\[ \stackrel{-}{x}=\frac{\sum _{i=1}^{n}{x}_{i}}{n} \]


Algumas propriedades da média aritmética:


  • somando-se (ou subtraindo-se) cada um dos elementos do conjunto de dados por uma constante arbitrária qualquer \(k\), a média aritmética ficará adicionada (ou subtraída) dessa essa constante \(k\)


alturas_ad=alturas+0.05

par(mfrow=c(1,2))

stripchart(alturas,method = "stack",  at=0.5, 
main="",pch = 20,
col="blue", cex=1, xlab="Alturas originais dos estudantes (m)", 
ylab="Quantidades observadas (un)")
abline(v=mean(alturas), col="red") 
text(mean(alturas)-0.2, 1, "Média=1,69 m", col = "red", srt=90) 

stripchart(alturas_ad,method = "stack",  at=0.5, 
main="",pch = 20,
col="blue", cex=1, xlab="Alt. dos estudantes (m) adic. de 5cm", 
ylab="Quantidades observadas (un)")
abline(v=mean(alturas_ad), col="red") 
text(mean(alturas_ad)-0.2, 1, "Média=1,74 m", col = "red", srt=90)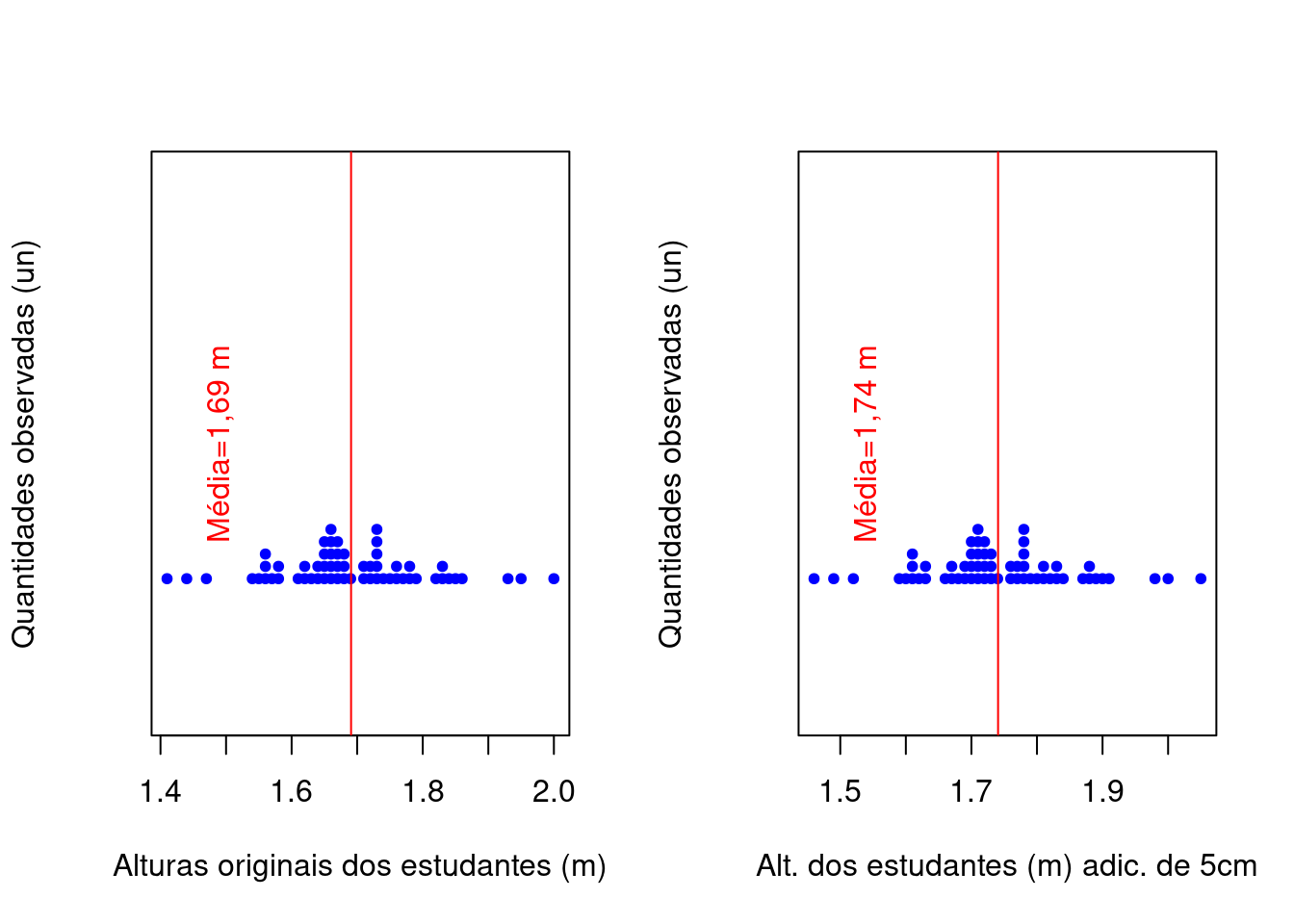
Mudanças na média pela adição (subtração) de uma constante $k=0.05$

Figure 3.3: Mudanças na média pela adição (subtração) de uma constante \(k=0.05\)


  • multiplicando-se (ou dividindo-se) cada um dos elementos do conjunto de dados por uma constante arbitrária \(k\), a média aritmética ficará multiplicada (ou dividida) por essa constante \(k\)


alturas_mult=alturas*1.2

par(mfrow=c(1,2))

stripchart(alturas,method = "stack",  at=0.5, 
main="",pch = 20,
col="blue",  xlab="Alturas originais dos estudantes (m)", 
ylab="Quantidades observadas (un)")
abline(v=mean(alturas), col="red") 
text(mean(alturas)-0.1, 1, "Média=1,69 m", col = "red", srt=90) 


stripchart(alturas_mult,method = "stack",  at=0.5, 
main="",pch = 20,
col="blue",  xlab="Alt. dos estudantes (m) mult. por 1,2", 
ylab="Quantidades observadas (un)")
abline(v=mean(alturas_mult), col="red") 
text(mean(alturas_mult)-0.1, 1, "Média= 2,02 m", col = "red", srt=90)
Mudanças na média pela multiplicação (divisão) de uma constante $k=1.2$

Figure 3.4: Mudanças na média pela multiplicação (divisão) de uma constante \(k=1.2\)


  • a soma dos desvios observados entre cada um dos valores assumidos pela variável \(X\) e sua média \(\stackrel{-}{x}\) é nula;
  • a soma dos quadrados dos desvios é mínima;
  • em uma distribuição de frequências, a soma dos produtos dos desvios entre a média o valor médio de cada uma das classes, pelas respectivas frequências é nula; e,
  • multiplicando-se (ou dividindo-se) todas as frequências de uma distribuição por uma constante arbitrária, a média aritmética não se altera.


Usando os dados das medidas das alturas dos 60 estudantes teremos o seguinte valor para a média:


round(mean(alturas),2)
## [1] 1.69

3.3.1.2 Moda


Moda é o valor que ocorre com maior frequência na amostra. Uma amostra pode se apresentar como:


  • unimodal;
  • bimodal;
  • plurimodal; ou,
  • amodal.


tab_alturas=table(alturas)

tab_alturas
## alturas
## 1.41 1.44 1.47 1.54 1.55 1.56 1.57 1.58 1.61 1.62 1.63 1.64 1.65 1.66 1.67 1.68 
##    1    1    1    1    1    3    1    2    1    2    1    2    4    5    4    3 
## 1.69 1.71 1.72 1.73 1.74 1.75 1.76 1.77 1.78 1.79 1.82 1.83 1.84 1.85 1.86 1.93 
##    1    2    2    5    1    1    2    1    2    1    1    2    1    1    1    1 
## 1.95    2 
##    1    1
barplot(tab_alturas,
        main="Valores observados da alturas dos estudantes",
        xlab="Altura (cm)",
        ylab="Quantidade observada (un)",
        ylim=c(0,6),
        col="blue",
        las=0, 
        hor="FALSE")
Bimodal: 1,66 m e 1,73 m

Figure 3.5: Bimodal: 1,66 m e 1,73 m


Usando os dados das medidas das alturas dos 60 estudantes teremos os seguintes valores para a moda:


# função em R para extrair a moda:

Modes <- function(x) {
  ux <- unique(x)
  tab <- tabulate(match(x, ux))
  ux[tab == max(tab)]
}

Modes(alturas)
## [1] 1.66 1.73

3.3.2 Medidas de dispersão (variabilidade)


O conhecimento de uma medida de tendência central nos provê uma informação útil mas incompleta. As medidas de dispersão nos ajudam a ter uma perspectiva melhor dos dados.


  • amplitude total dos dados;
  • desvio padrão (variância): é considerada a mais útil das medidas de dispersão;
  • coeficiente de variação; e,
  • unidades padronizadas.


Diferentes tipos quanto à dimensão (unidade):


  • medidas absolutas são aquelas expressas na mesma unidade de medida da variável do fenômeno estudado (\(m;kg;\frac{R\$}{mês};\dots\));
  • medidas relativas são adimiensionais e assim podem ser usadas para se comparar a variabilidade de dois ou mais conjuntos de dados, mesmo quando as variáveis se refiram a diferentes fenômenos ou que sejam expressas, originalmente, em diferentes unidades.


3.3.2.1 Amplitude total dos dados


A amplitude total dos dados é a simples diferença entre o maior e o menor dos valores observados:


\[ A=x_{max} - x_{min} \]


3.3.2.2 Estimação da variância (e desvio padrão)


Sejam \(x_{1}, x_{2}, ..., x_{n}\) os \(n\) valores assumidos pela variável \(X\). Dá-se o nome de desvios a contar da média as diferenças entre cada uma das observações e a média: \(x_{i} - \stackrel{-}{x}\) com \(i=1,2,...,n\).


Não é possível considerar a possibilidade de se adotar o valor médio desses desvios pois uma das propriedades da média é que a soma dos desvios em torno de si é nula.


\[ \stackrel{-}{d} = \frac{\sum _{i=1}^{n}\left(x_{i}-\stackrel{-}{x}\right)}{n} \] \[ \sum _{i=1}^{n}\left(x_{i}-\stackrel{-}{x}\right)=0 \]


constitui-se numa restrição linear dos desvios porque qualquer \(n-1\) deles completamente determina o outro. Tampouco se considera a possibilidade de se adotar o valor médio desses desvios em módulo, pelas dificuldades teóricas em problemas de inferência.


\[ \stackrel{-}{d} = \frac{\sum _{i=1}^{n}\left|x_{i}-\stackrel{-}{x}\right|}{n} \]


Uma alternativa é adotar o valor médio do quadrado desses desvios.


\[ S^{2}=\frac{\sum _{i=1}^{n}\left(x_{i}-\stackrel{-}{x}\right)^{2}}{n-1} \]


ou,


\[ S^{2}=\frac{1}{(n-1)} \times \left[ \sum _{i=1}^{n} (x_{i}^{2}) - \frac{({\sum _{i=1}^{n}x_{i})}^{2} }{n}\right] \]


Diz-se que a variância amostral (variância ajustada) possui \((n-1)\) graus de liberdade, denotado pela letra grega \(\nu\). A perda de um grau de liberdade deve-se à necessidade de se substituir a média populacional desconhecida (\(\mu\)) por sua estimativa amostral (\(\stackrel{-}{x}\)), deduzida a partir dos dados coletados.


Pode-se demonstrar que em razão dessa restrição a melhor estimativa para a variância populacional é obtida dividindo-se a soma dos quadrados dos desvios por \((n-1)\). Assim \(S^{2}\) será um estimador não tendencioso para a variância amostral ao ser dividido por \((n-1)\).


IC.Na = function (N, n, mu, sigma) {
  dados=data.frame()
  plot(0, 0, 
       type="n", 
       xlim=c(sigma-0.1*sigma,sigma+0.1*sigma), 
       ylim=c(0,N), 
       bty="l",
       xlab="Desvio padrão", 
       ylab="Amostras extraídas", 
       main=paste0("Flutuação dos valores dos desvios padrão \nobtidos em ", N," amostras de tamanho ",n), 
       sub=paste0("A população de origem tem uma distribuição ~ N  (\u03bc:",mu," ; \u03c3:", sigma,")"))
  abline(v=sigma, col='darkgreen', lwd=2, lty=2)
for (i in 1:N) {
  x = rnorm(n, mu, sigma)
  media = mean(x)
  sd = sqrt(sum((x-mean(x))^2)/(n-1))
  sd_vies = sqrt(sum((x-mean(x))^2)/(n))
  temp=cbind(mu, media, sd, sd_vies)
  dados=rbind(dados, temp)
  plotx = c(sd)
  ploty = c(i,i)
  if ( sd < sigma) points(sd, i, col="blue",cex=1)+text(y=i+3,x=sd, labels=round(sd,3), cex=1, col='blue')
  else 
    points(sd, i, col="blue", cex=1)+text(y=i+3,x=sd, labels=round(sd,3), cex=1, col='blue') 
  plotx = c(sd_vies)
  ploty = c(i,i)
  if ( sd_vies < sigma) points(sd_vies, i, col="red",cex=1)+text(y=i+3,x=sd_vies, labels=round(sd_vies,3), cex=1, col='red')
  else 
    points(sd_vies, i, col="red", cex=1)+text(y=i+3,x=sd_vies, labels=round(sd_vies,3), cex=1, col='red') 
} 
abline(v=mean(dados$sd), col='blue', lwd=2, lty=2)
abline(v=mean(dados$sd_vies), col='red', lwd=2, lty=2)
}


IC.Na(N=100, n=15, mu=170, sigma=7)
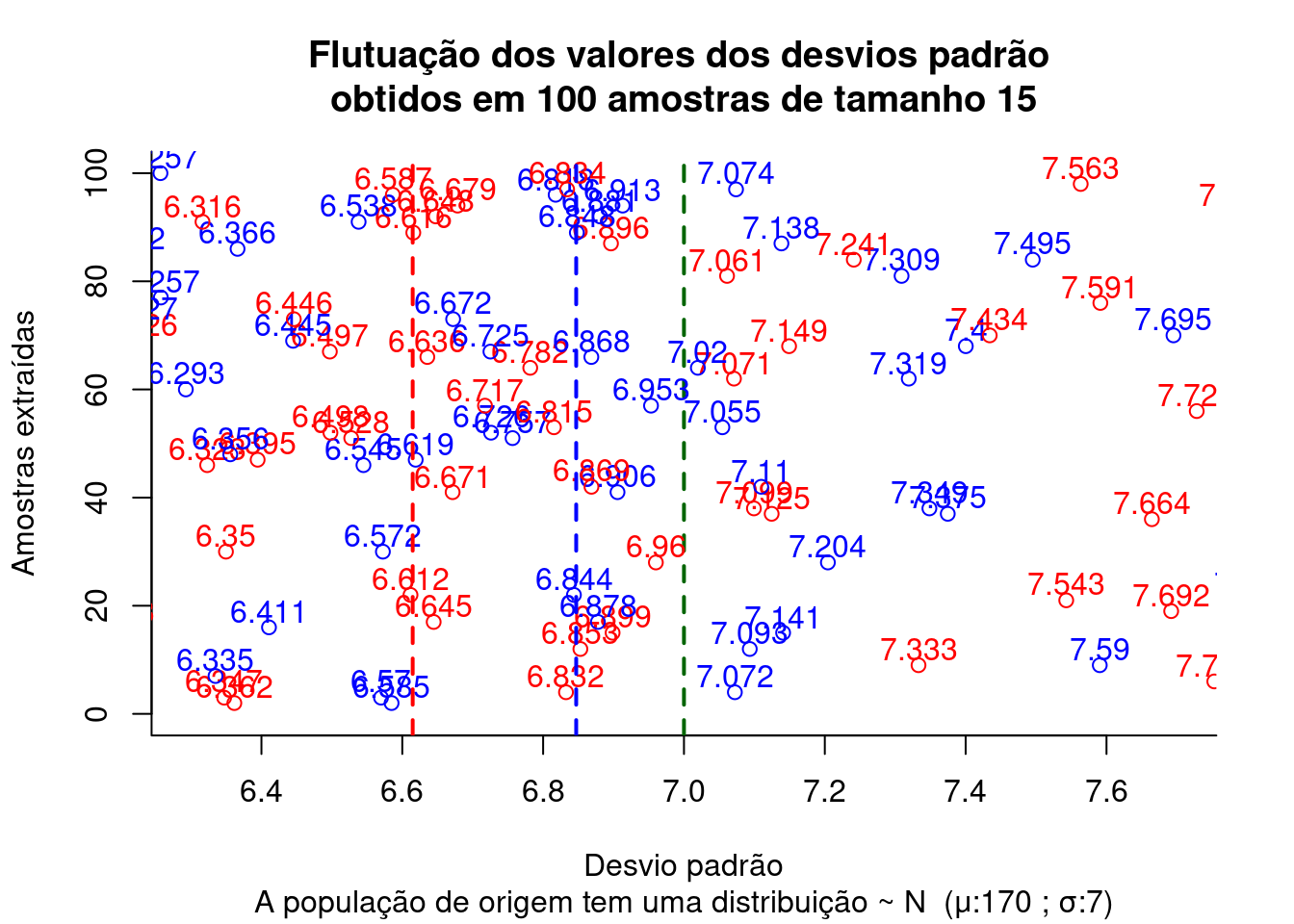
Flutuação dos valores do desvio padrão obtidos pelo estimador não viesado (em azul) e pelo estimador viesado (em vermelho) para diversas amostras extraídas de uma mesma população distribuição $\sim N (\mu; \sigma)$ (em verde o desvio padrão populacional, em azul a média dos desvios padrão amostrais correta e em vermelho a estimada de modo viesado)

Figure 3.6: Flutuação dos valores do desvio padrão obtidos pelo estimador não viesado (em azul) e pelo estimador viesado (em vermelho) para diversas amostras extraídas de uma mesma população distribuição \(\sim N (\mu; \sigma)\) (em verde o desvio padrão populacional, em azul a média dos desvios padrão amostrais correta e em vermelho a estimada de modo viesado)


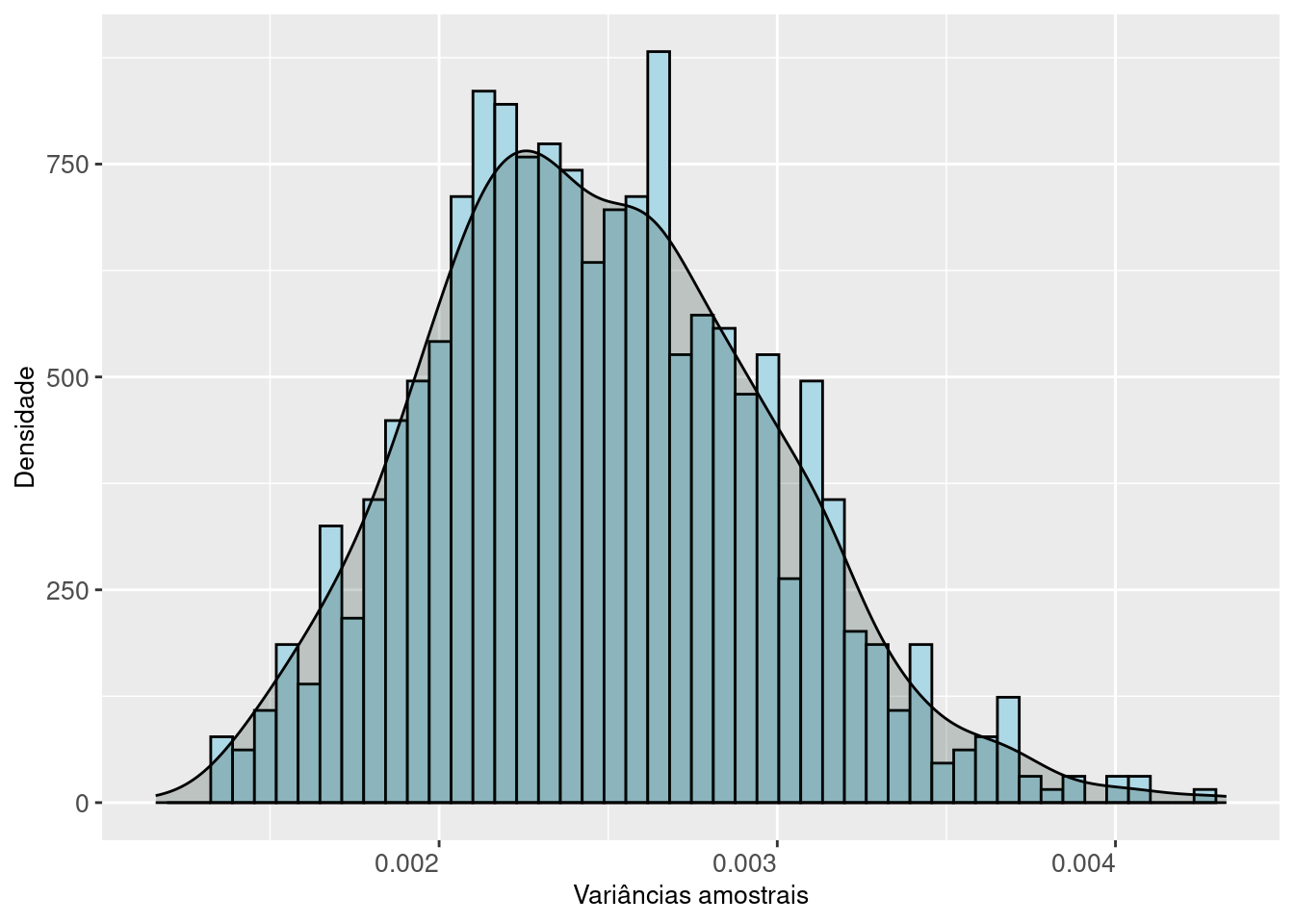
A distribuição das variâncias amostrais segue uma curva aproximada pela distribuição Qui-quadrado com (n-1) graus de liberdade

Figure 3.7: A distribuição das variâncias amostrais segue uma curva aproximada pela distribuição Qui-quadrado com (n-1) graus de liberdade


Uma medida de dispersão que apresenta a mesma unidade que a das observações originais é o desvio-padrão, definido como a raiz quadrada positiva da variância.


\[ S= \sqrt{\frac{\sum _{i=1}^{n}\left(x_{i}-\stackrel{-}{x}\right)^{2}}{n-1}} \]


Tanto a variância quanto o desvio padrão indicam, em média, qual será o erro (desvio) cometido ao tentar substituir cada observação pela medida resumo do conjunto de dados (média).


Usando os dados das medidas das alturas dos 60 estudantes teremos o seguinte valor para a variância (com unidade igual a \(m^{2}\)) e o desvio padrão (com unidade igual a \(m\)):


# Variãncia
var(alturas)
## [1] 0.0130809
# Desvio padrão
sd(alturas) 
## [1] 0.1143718

Propriedades da variância:


  • somando-se (ou subtraindo-se) cada um dos elementos do conjunto de dados por uma constante arbitrária, a variância (e o desvio padrão) não se altera; e,
  • multiplicando-se (ou dividindo-se) cada um dos elementos do conjunto de dados por uma constante arbitrária, a variância ficará multiplicada (ou dividida) pelo quadrado dessa constante. O desvio padrão fica multiplicado (ou dividido) por essa constante


# Adicionando-se uma constante k=0.05
alturas_ad=alturas+0.05

# Variância não se altera
var_ad= var(alturas_ad)
var_ad
## [1] 0.0130809
# Multiplicando-se uma constante k=1.2
alturas_mult=alturas*1.2

# Variância fica multiplicada (dividida) pelo quadrado dessa constante)
var(alturas_mult)
## [1] 0.0188365
all.equal(var(alturas_mult), var(alturas)*(1.2^2)) 
## [1] TRUE

3.3.2.3 Coeficiente de variação.


O coeficiente de variação (uma medida adimensional) é dado pela razão do desvio padrão pela média:


\[ CV(\%)= 100\cdot(\frac{s}{\stackrel{-}{x}}) \]



Classificação da variabilidade a partir da medida do Coeficiente de variação
Classificação Medida do Coeficiente de variação (CV %)
Baixo CV ≤ 10%
Médio 10% ≤ CV ≤ 20%
Alto 20% ≤ CV ≤ 30%
Muito alto CV ≥ 30%

3.3.3 Medidas de subdivisão (separatrizes)


Separatrizes (quantis) são medidas quantitativas que delimitam uma proporção de observações existentes em um conjunto de dados previamente ordenados com valores menores que ela.


Assim, se tomamrmos como exemplo a mediana, ela é dita uma separatriz (ou quantil) de 50% pois aproximadamente 50% dos dados de um conjunto possuem valores menores que ela.


Para se determinar qualquer separatriz necessitamos saber antes qual a posição que ela ocupa nos dados ordenados crescentemente: \(x_{1}<x_{2}< \dots< x_{n}\):


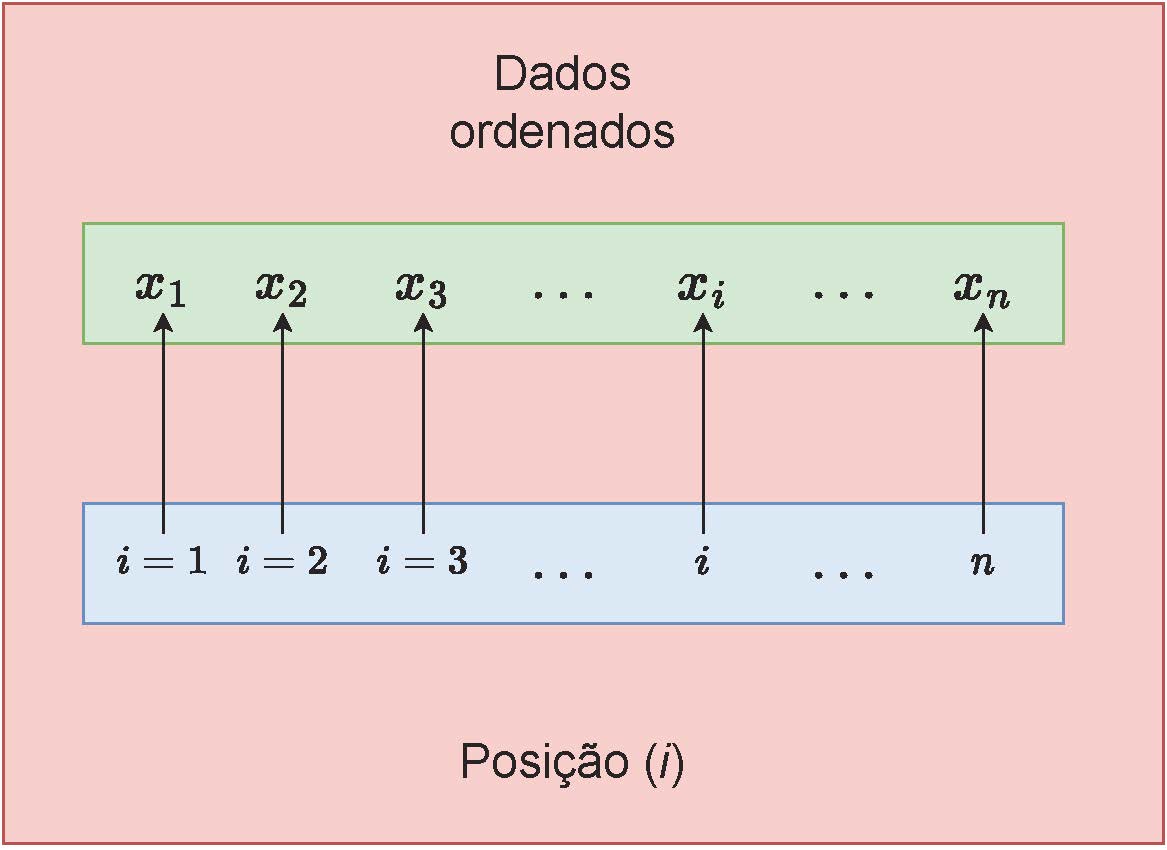
Entendendo a indexação de dados

Figure 3.8: Entendendo a indexação de dados


De modo geral, um quantil de ordem \(p\) (ou também \(p-quantil\), indicado por \(q_{p}\)) é uma medida separatriz onde \(p\) é uma proporção qualquer (limitada no intervalo 0 < p < 1), tal que 100\(p\)% das observações sejam menores que seu valor \(q_{p}\). Desse modo, o valor \(q_{p}\) de uma variável aleatória \(X\) remete à medida da probabilidade:


\[ P(X=x | x\leq q_{p})=p \]

Os quantis recebem diferentes nomes em função do modo como subdividem o conjunto de dados:


  • percentil (subdivisão em 100 partes): \(p_{1}, \dots, p_{99}\)
  • decis (subdivisão em 10 partes): \(d_{10}, \dots, d_{90}\)
  • quartis (subdivisão em 4 partes): \(Q_{1}, \dots, Q_{3}\)


Naturalmente que os valores de \(p_{50}\), \(d_{5}\) e \(Q_{2}\) são os mesmos posto tratarem-se de separatrizes que subdividem os dados na mesma propoção (50%).


Os quantis mais informativos (e que por essa razão são usados para um importante gráfico que mais adiante será exposto em detalhes - Boxplot) são: \


  • 1\(^{o}\) Quartil (\(q_{0,25}\)): 25% dos dados possuem valores abaixo desse valor e 75% estão acima;
  • 2\(^{o}\) Quartil ou mediana (\(q_{0,50}\)): 50% dos dados possuem valores abaixo desse valor e 50% estão acima; e,
  • 3\(^{o}\) Quartil (\(q_{0,75}\)): 75% dos dados possuem valores abaixo desse valor e 25% estão acima.


Todavia a medicina utiliza para muitos propósitos os percentis como, por exemplo, as curvas de crescimento idade \(versus\) altura.


De modo geral, para se calcular a posição L que um quantil qualquer de ordem p assume em um rol de dados há algumas regras empíricas:

\[ L_{p}=\frac{p}{100} \times (n)\\ L_{p}=\frac{p}{100} \times (n+1)\\ L_{p}=[\frac{p}{100} \times (n-1)]+1\\ \]

Onde:


  • p é a ordem do quantil em % (50% no caso mediana, por exemplo);
  • n é o número de dados do rol; e,
  • L é a posição do valor referente ao quantil desejado.


Os quartis calculados a partir das posições determinadas por essas regras aproximadamente subdividem o conjunto de dados em 25%, 50% e 75%.


Assim, para a determinação dos quartis pela primeira regra o valor de p seria:


  • para o primeiro quartil (\(Q_{1}\)): \(L_{q_{0,25}}=\frac{25}{100} \times (n)\);
  • para o segundo quartil (a mediana ou \(Q_{2}\)): \(L_{q_{0,50}}=\frac{50}{100} \times (n)\); ou,
  • para o terceiro quartil (\(Q_{3}\)): \(L_{q_{0,75}}=\frac{75}{100} \times (n)\).


Novamente podemos nos deparar com duas situações possíveis para o valor calculado para a posição L qualquer que seja a regra:


  • se valor calculado da posição L for um inteiro, nessa posição encontraremos o valor referente ao quantil desejado;
  • se o valor calculado da posição L for fracionário, o valor desse quantil será determinado pela média entre os dois valores dos dados que estão nas posições imediatamente anterior e imediatamente posterior à posição L calculada.


Juntamente com as observações mínima (\(x_{i}\)) e máxima (\(x_{n}\)), o 1\(^{o}\), 2\(^{o}\) e 3\(^{o}\) Quartis são importantes para se ter uma boa idéia da assimetria da distribuição dos dados.


Para uma distribuição simétrica (ou aproximadamente simétrica) deveremos observar (Distribuição Gaussiana):


  • a dispersão inferior: \(q_{2} - x_{1} \approx x_{n} - q_{2}\) à dispersão superior ;
  • \(q_{2} - q_{1} \approx q_{3} - q_{2}\); e,
  • \(q_{1} - x_{1} \approx x_{n} - q_{3}\).


Para nosso conjunto de dados, segundo a regra empírica apresentada teremos as seguintes posições para determinação dos valores dos quartis:


  • para o primeiro quartil:

\[\begin{align*} L_{Q_{1}} & =\frac{p}{100} \times (n) \\ & =\frac{25}{100} \times (60) \\ & = 0,25*60 \\ & = 15 \end{align*}\]

  • para o segundo quartil:

\[\begin{align*} L_{Q_{2}} & =\frac{p}{100} \times (n) \\ & =\frac{50}{100} \times (60) \\ & = 0,5*60 \\ & = 30 \end{align*}\]


- para o terceiro quartil:

\[\begin{align*} L_{Q_{3}} & =\frac{p}{100} \times (n) \\ & =\frac{75}{100} \times (60) \\ & = 0,75*60 \\ & = 45 \end{align*}\]


E os quartis serão:


-\(Q_{1}\)=1,63
-\(Q_{2}\)=1,67
-\(Q_{3}\)=1,75


Há muitos modos de se estabelecer os quantis descritos na literatura. O próprio R apresenta 9 modos diferentes:


quantile(alturas, type=1)
##   0%  25%  50%  75% 100% 
## 1.41 1.63 1.67 1.75 2.00
quantile(alturas, type=2)
##    0%   25%   50%   75%  100% 
## 1.410 1.635 1.675 1.755 2.000
quantile(alturas, type=3)
##   0%  25%  50%  75% 100% 
## 1.41 1.63 1.67 1.75 2.00
quantile(alturas, type=4)
##   0%  25%  50%  75% 100% 
## 1.41 1.63 1.67 1.75 2.00
quantile(alturas, type=5)
##    0%   25%   50%   75%  100% 
## 1.410 1.635 1.675 1.755 2.000
quantile(alturas, type=6)
##     0%    25%    50%    75%   100% 
## 1.4100 1.6325 1.6750 1.7575 2.0000
quantile(alturas, type=7)
##     0%    25%    50%    75%   100% 
## 1.4100 1.6375 1.6750 1.7525 2.0000
quantile(alturas, type=8)
##       0%      25%      50%      75%     100% 
## 1.410000 1.634167 1.675000 1.755833 2.000000
quantile(alturas, type=9)
##       0%      25%      50%      75%     100% 
## 1.410000 1.634375 1.675000 1.755625 2.000000


Para grandes conjuntos de dados a diferença entre os quantis determinados sob esses diferentes modos será desprezível.


## Padronização (z-scores)


À conversão do valor assumido por uma variável em unidades de desvio padrão acima (ou abaixo) do valor médio de sua distribuição é dado o nome de padronização. Essa métrica permite comparações com outras, procedentes de outros fenômenos.


Para padronizar (achar o seu z-score Z) o valor de uma variável procede-se segundo a fórmula:


\[ Z=\frac{x_{i} - \stackrel{-}{x}}{s} \]


O valor \(Z\) expressa quantos desvios esse dado está acima (ou abaixo) da média da distribuição.


Pelo Teorema de Tchebichev pode-se estimar a probabilidade mínima dos dados situados a certa distância de \(k\) desvios da média dessa distribuição:


\[ P(|X-\mu|\ge k\sigma) \leq 1 - \frac{1}{k^{2}} \]


Assim, se \(k=2\) ao menos 75% das observações devem estar entre a média e dois desvios padrões acima ou abaixo da média.


med=round(mean(alturas),2)
desv= round(sd(alturas),2)


No exemplo das alturas dos estudantes temos a média de 1.69 m e um desvio padrão de 0.11 m. Assim, ao menos 75% das alturas deverão estar entre 1.47 m e 1.91 m.


sort(alturas)
##  [1] 1.41 1.44 1.47 1.54 1.55 1.56 1.56 1.56 1.57 1.58 1.58 1.61 1.62 1.62 1.63
## [16] 1.64 1.64 1.65 1.65 1.65 1.65 1.66 1.66 1.66 1.66 1.66 1.67 1.67 1.67 1.67
## [31] 1.68 1.68 1.68 1.69 1.71 1.71 1.72 1.72 1.73 1.73 1.73 1.73 1.73 1.74 1.75
## [46] 1.76 1.76 1.77 1.78 1.78 1.79 1.82 1.83 1.83 1.84 1.85 1.86 1.93 1.95 2.00
# Duas observações menores que 1,47m e trẽs maiores que 1,91m.
# Assim, 54 observações dentro do intervalo, equivalendo a 91,66% do total.