3.6 Apresentação gráfica de dados

Uma apresentação na forma gráfica torna ainda mais fácil a visualização das informações contidas nos dados. Há uma gama enorme de gráficos para a representação de dados a depender de sua natureza (qualitativa ou quantitativa).

3.6.1 Gráficos para uma variável qualitativa

• ranking: barras;
• parte em relação ao todo: setores;

3.6.1.1 Colunas

A partir das tabelas mostradas na seção 3.5.1.1 Dados qualitativos em entrada única poderíamos eleborar a apresentação gráfica na forma de Gráficos de colunas:

desembarque=c('AM','AM','A','A','A','AM','EU','EU','EU','EU','AM','AS','AS','AS','OC','AS','EU','AM')
tab_desembarque=table(desembarque)

barplot(tab_desembarque,
        main="Desembarques no terminal internacional A em Cumbica \n(10/10/2021: 8 h 00min às 12 h 00 min)",
        sub= "Continente de procedência: América: AM; África: A; Europa: EU; Ásia: AS; Oceania: OC \nfonte: próprio autor",
        xlab="",
        ylab="Quantidade observada (un)",
        ylim=c(0,6),
        col="blue",
        las=0, 
        hor="FALSE")

Figure 3.14: Gráfico de barras dos dados observados no terminal de desembarque internacional do aeroporto

library(ggplot2)
dados=data.frame(tipo=c("Casal com filhos",
                          "Casal sem filhos",
                          "Solteiro, s/parceiro",
                          "Morando sozinho",
                          "Outros domicíclios"),
                 quant=c(24.1, 31.1, 
                       19.1, 30.1,
                       6.7))

ggplot(dados, aes(x=tipo, y=quant, color=tipo)) +
geom_bar(stat="identity", position=position_dodge())+
ggtitle("Estrutura domiciliar dos Estados Unidos, 2005") +
theme(legend.position="bottom")+
geom_text(aes(label=quant), vjust=1.6, color="white", position = position_dodge(0.9), size=3.5)+
scale_fill_brewer(palette="Paired")+
theme_minimal()+
xlab("")  +
ylab("Frequência absoluta observada (milhões)")+
labs(colour = "Tipos de domicílios")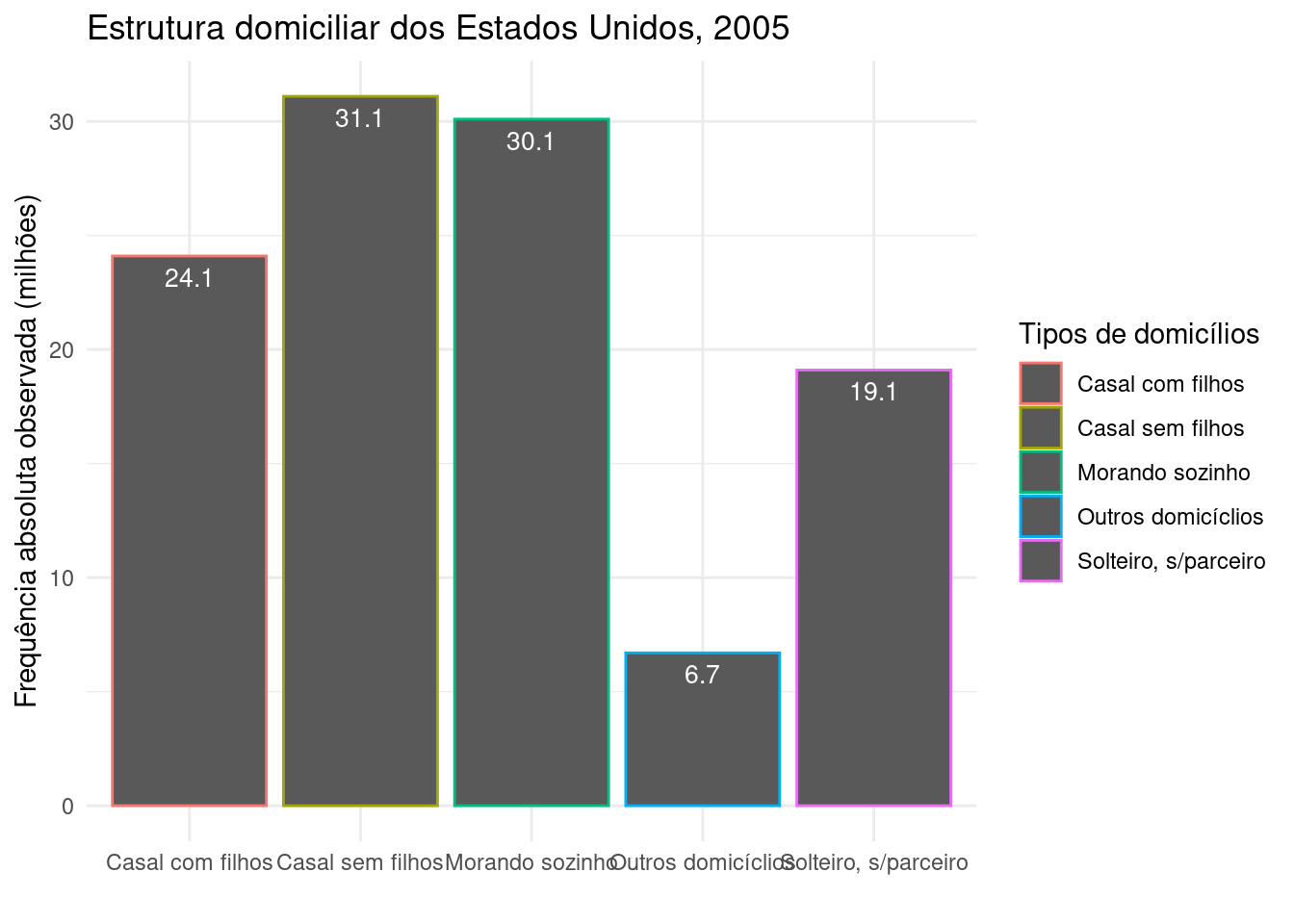 

Figure 3.15: Gráfico de barras da estrutura domiciliar dos Estados Unidos

3.6.1.2 Setores

Em um Gráfico de setores a representação das quantidades está associada a uma fração do comprimento de um círculo. Para sua confecção considera-se a proporção da quantidade observada específica da quantidade total de dados, expressa na forma de fração do ângulo de um setor circular em relação ao ângulo interno total de um círculo (360^o).

library(scales)

## 
## Attaching package: 'scales'

## The following objects are masked from 'package:formattable':
## 
##     comma, percent, scientific

library(ggplot2)

desembarques_classes=data.frame(
  group = c("América","África","Europa","Ásia","Oceania"),
  value = c(5,3,5,4,1))


blank_theme=theme_minimal()+
  theme(
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    panel.border = element_blank(),
    panel.grid=element_blank(),
    axis.ticks = element_blank(),
    plot.title=element_text(size=14, face="bold")
  )

ggplot(desembarques_classes, aes(x="", y=value, fill=group)) +
  blank_theme +
  scale_fill_brewer("Blues")+
  labs(title="Desembarques no terminal internacional A em Cumbica", 
          subtitle="(10/10/2021: 8 h 00min às 12 h 00 min)",
           caption = "Fonte: próprio autor") +
  theme(axis.text.x=element_blank()) +
  geom_bar(width = 1, stat = "identity") +
  coord_polar("y", start=0) +
  geom_text(aes(y = value/2 + c(0, cumsum(value)[-length(value)]),
                label = percent(value/18 )), size=5)+
  guides(fill = guide_legend(title = "Legenda",
                             label.position = "right",
                             title.position = "top", title.vjust = 1))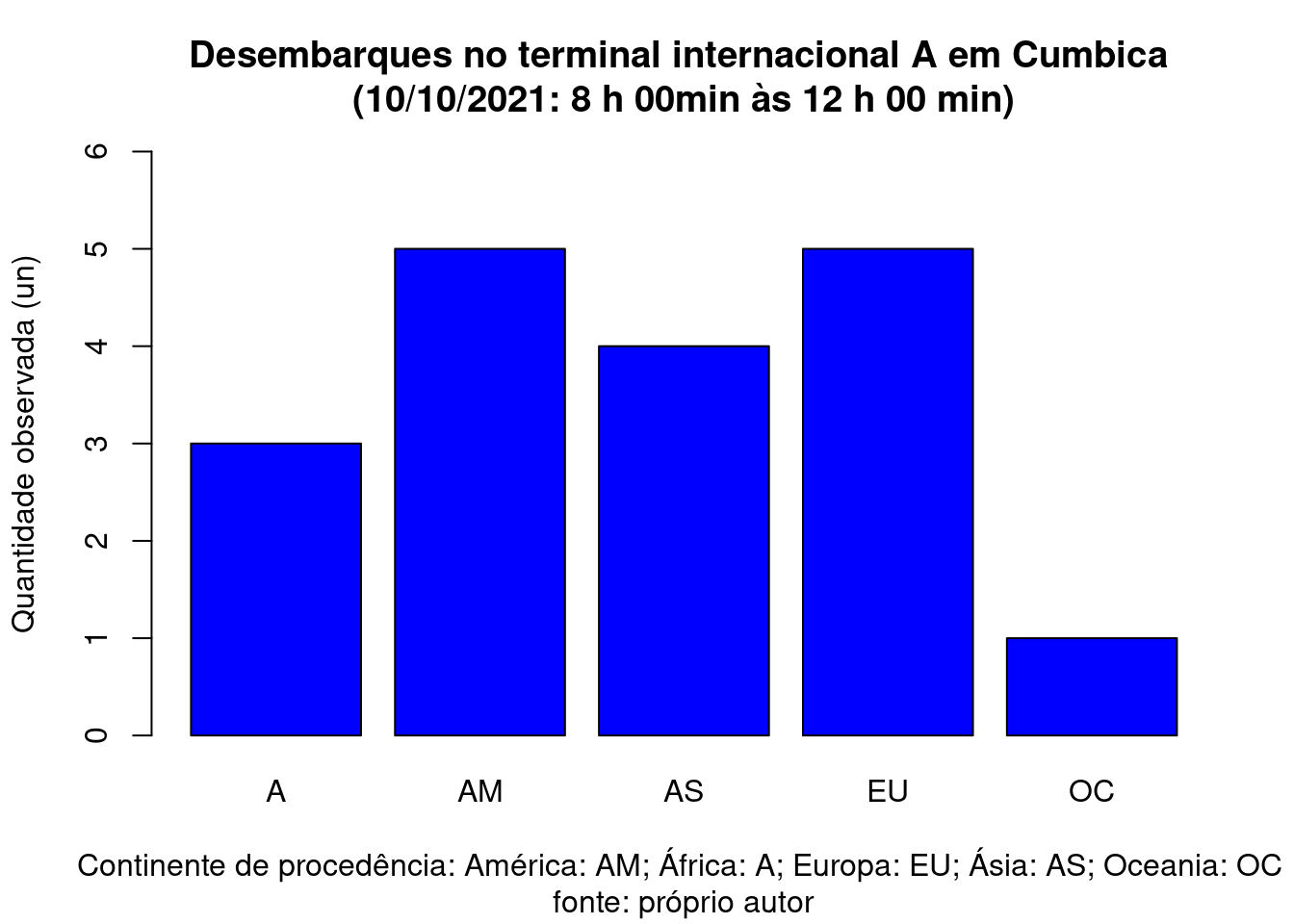 

Figure 3.16: Gráfico de setores dos desembarques observados no terminal de desembarque internacional do aeroporto

library(ggplot2)
library(scales)

blank_theme=theme_minimal()+
  theme(
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    panel.border = element_blank(),
    panel.grid=element_blank(),
    axis.ticks = element_blank(),
    plot.title=element_text(size=14, face="bold")
  )

bp=ggplot(dados, aes(x="", y=quant, fill=tipo))+
  geom_bar(width = 1, stat = "identity")
pie=bp + coord_polar("y", start=0)
pie + 
  scale_fill_brewer("Blues")+
  blank_theme +
  theme(axis.text.x=element_blank()) +
  geom_text(aes(x =  1.2,label = quant), position = position_stack(vjust = 0.5)) +
  ggtitle("Estrutura domiciliar dos Estados Unidos, 2005") +
  theme(legend.position = "right", legend.justification = "center", legend.direction = "vertical",
        legend.spacing.x = unit(0.5, 'cm'),legend.spacing.y = unit(0.5, 'cm'))+
  guides(fill = guide_legend(title = "Tipos de domicílios",
                             label.position = "right",
                             title.position = "top", title.vjust = 1))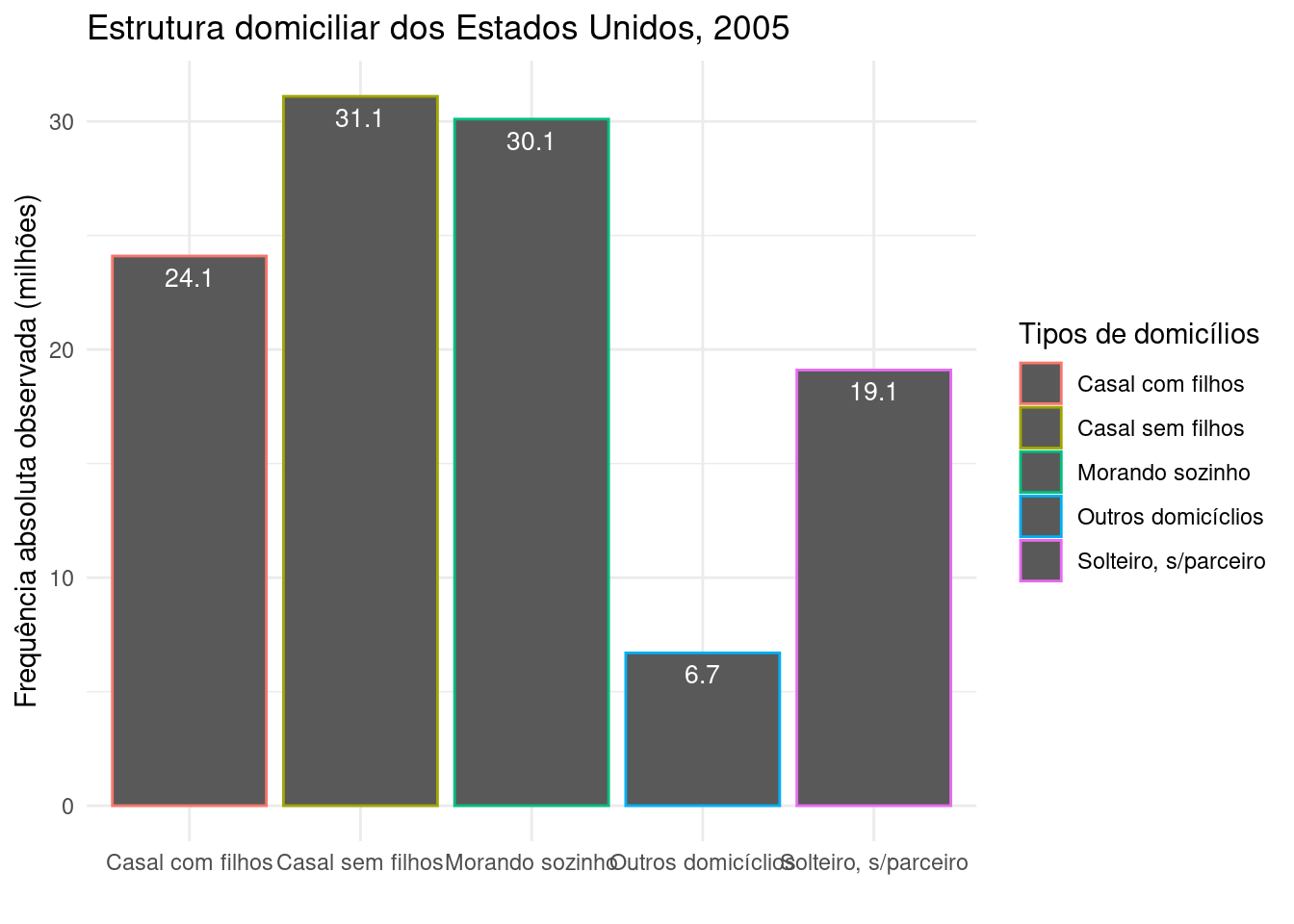 

Figure 3.17: Gráfico de setores da estrutura domiciliar dos Estados Unidos

3.6.1.3 Colunas para dados em uma tabela de dupla entrada

library(ggplot2)             # Carrega a biblioteca ggplot2

# Dados fornecidos
casal_com_filho_democratas <- 3478
casal_com_filho_republicano <- 2136
casal_sem_filho_democratas <- 2209
casal_sem_filho_republicano <- 2177

# Criar um dataframe com os dados
dados <- data.frame(
  Categoria = c("Com Filhos", "Com Filhos", "Sem Filhos", "Sem Filhos"),
  Partido = c("Democratas", "Republicanos", "Democratas", "Republicanos"),
  Contagem = c(casal_com_filho_democratas, casal_com_filho_republicano,
               casal_sem_filho_democratas, casal_sem_filho_republicano)
)

# Criar o gráfico de barras empilhadas
ggplot(dados, aes(x = Categoria, y = Contagem, fill = Partido)) +
  geom_bar(stat = "identity") +
  labs(title = "Contagem de Votos por Categoria e Partido (Censo dos EUA,2005)",
       x = "Categoria",
       y = "Contagem") +
  scale_fill_manual(values = c("Democratas" = "lightgreen", "Republicanos" = "lightblue")) +
  theme_minimal()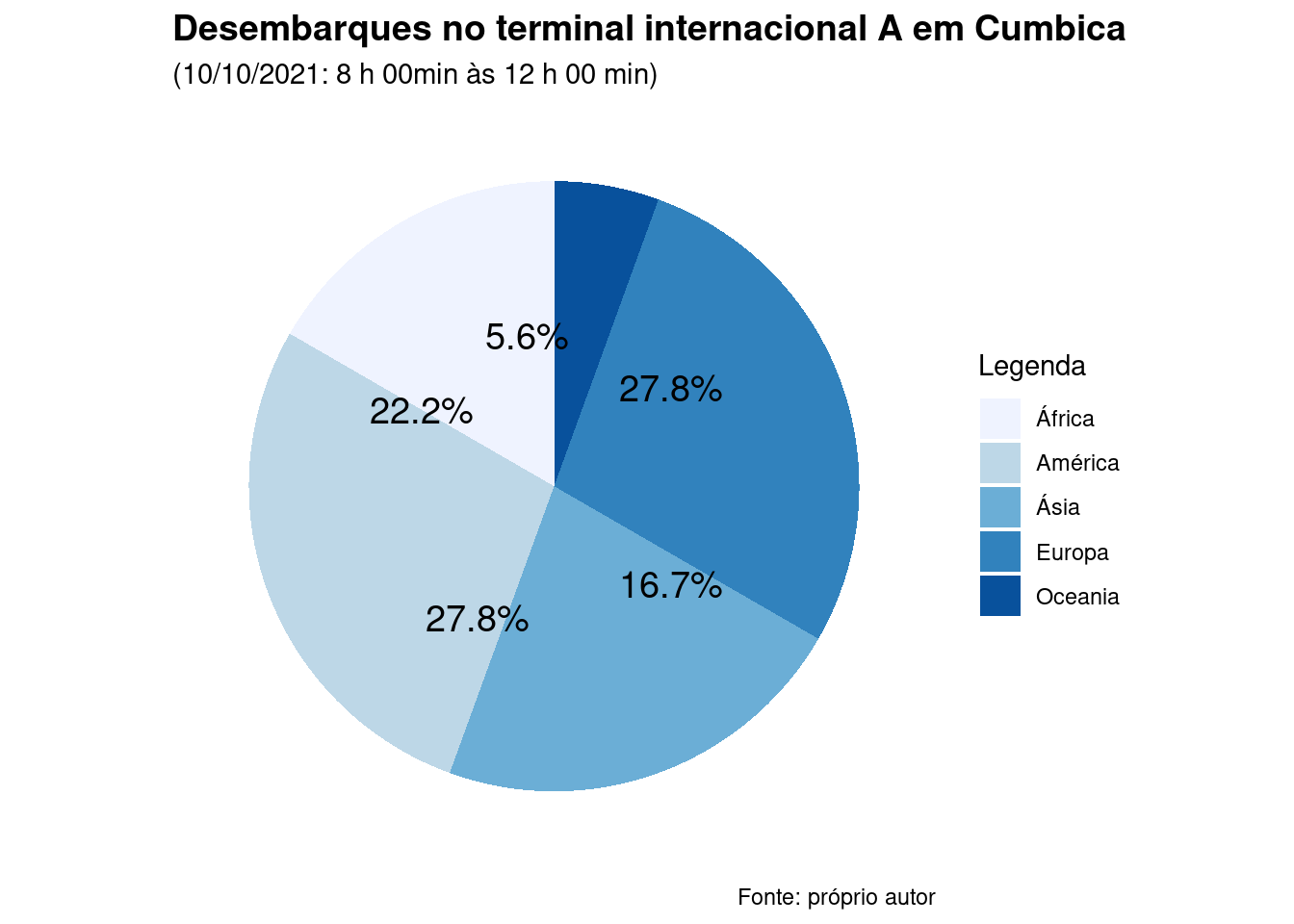

Figure 3.18: Gráfico de barras da estrutura familiar em relação à inclinação partidária nos Estados Unidos

library(ggplot2)             # Carrega a biblioteca ggplot2

# Dados fornecidos
fumantes_filho_bp = 275
fumantes_filho_pn = 2144
n_fumantes_filho_bp = 311
n_fumantes_filho_pn = 6640

# Criar um dataframe com os dados
dados <- data.frame(
  Risco = c("Fumante", "Fumante", "Não fumante", "Não fumante"),
  Peso = c("Baixo peso", "Peso normal", "Baixo peso", "Peso normal"),
  Contagem = c(fumantes_filho_bp, fumantes_filho_pn,
               n_fumantes_filho_bp, n_fumantes_filho_pn)
)

# Criar o gráfico de barras empilhadas
ggplot(dados, aes(x = Risco, y = Contagem, fill = Peso)) +
  geom_bar(stat = "identity") +
  labs(title = "Peso de recém nascidos em Pelotas (RS, 1982)",
       x = "Exposição ao risco",
       y = "Contagem") +
  scale_fill_manual(values = c("Baixo peso" = "gray", "Peso normal" = "lightgreen")) +
  theme_minimal()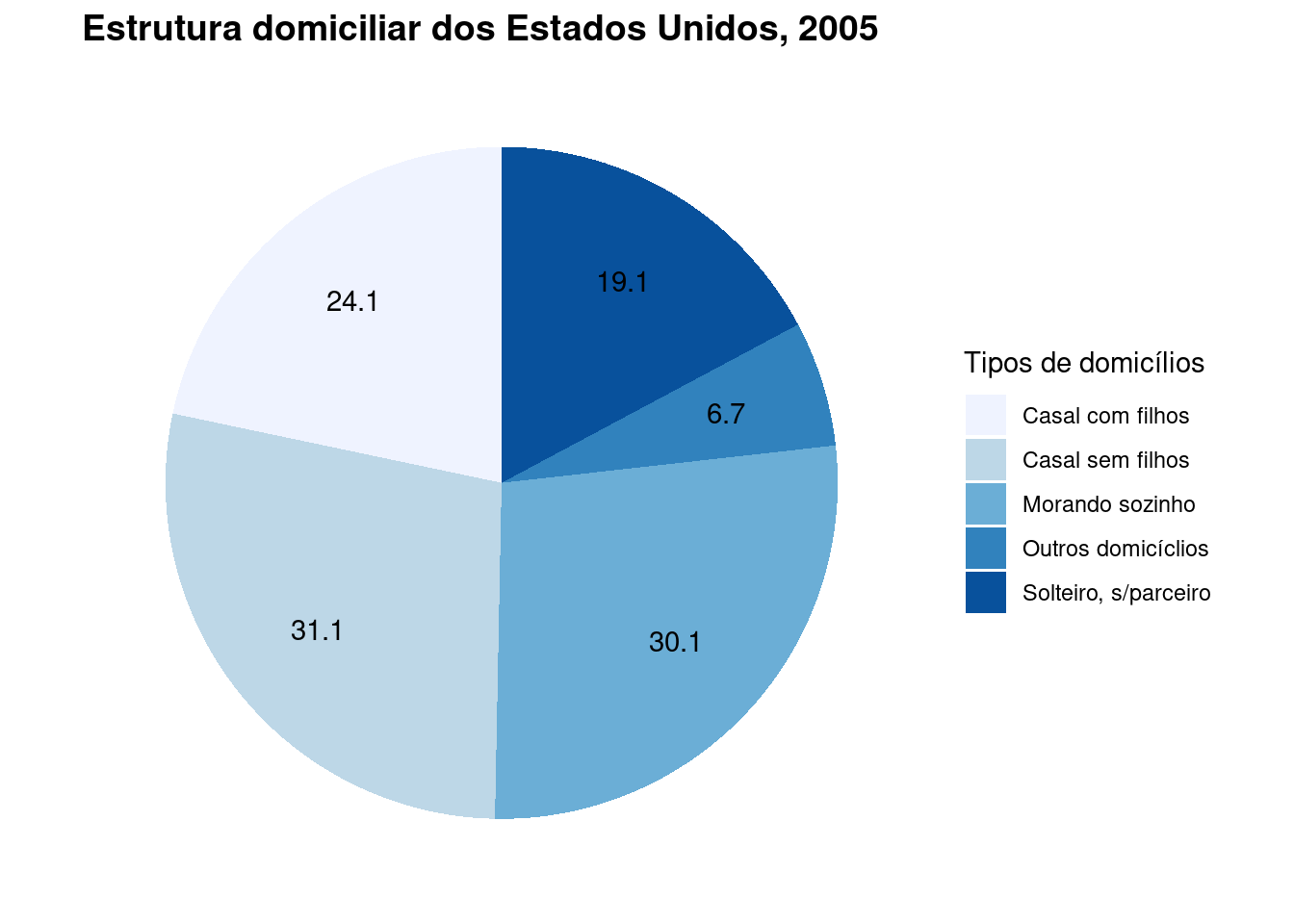

Figure 3.19: Gráfico de barras da exposição ao fator de risco e o efeito

3.6.2 Gráficos para uma variável quantitativa

• ranking: barras;
• parte em relação ao todo: setores;
• dispersão unidimensional;
• distribuição: histograma e o box plot.

3.6.2.1 Barras

Se modificarmos o diagrama de ramos e folhas dos comprimentos e quantidades observadas, representando cada uma das alturas medidas por um retângulo cujas alturas sejam proporcionais à quantidade contada de cada uma dessas alturas teremos um Gráfico de barras.

tab_alturas=table(alturas)

barplot(tab_alturas,
        main="Valores observados da alturas dos estudantes",
        xlab="Altura (cm)",
        ylab="Quantidade observada (un)",
        ylim=c(0,6),
        col="blue",
        las=0, 
        hor="FALSE")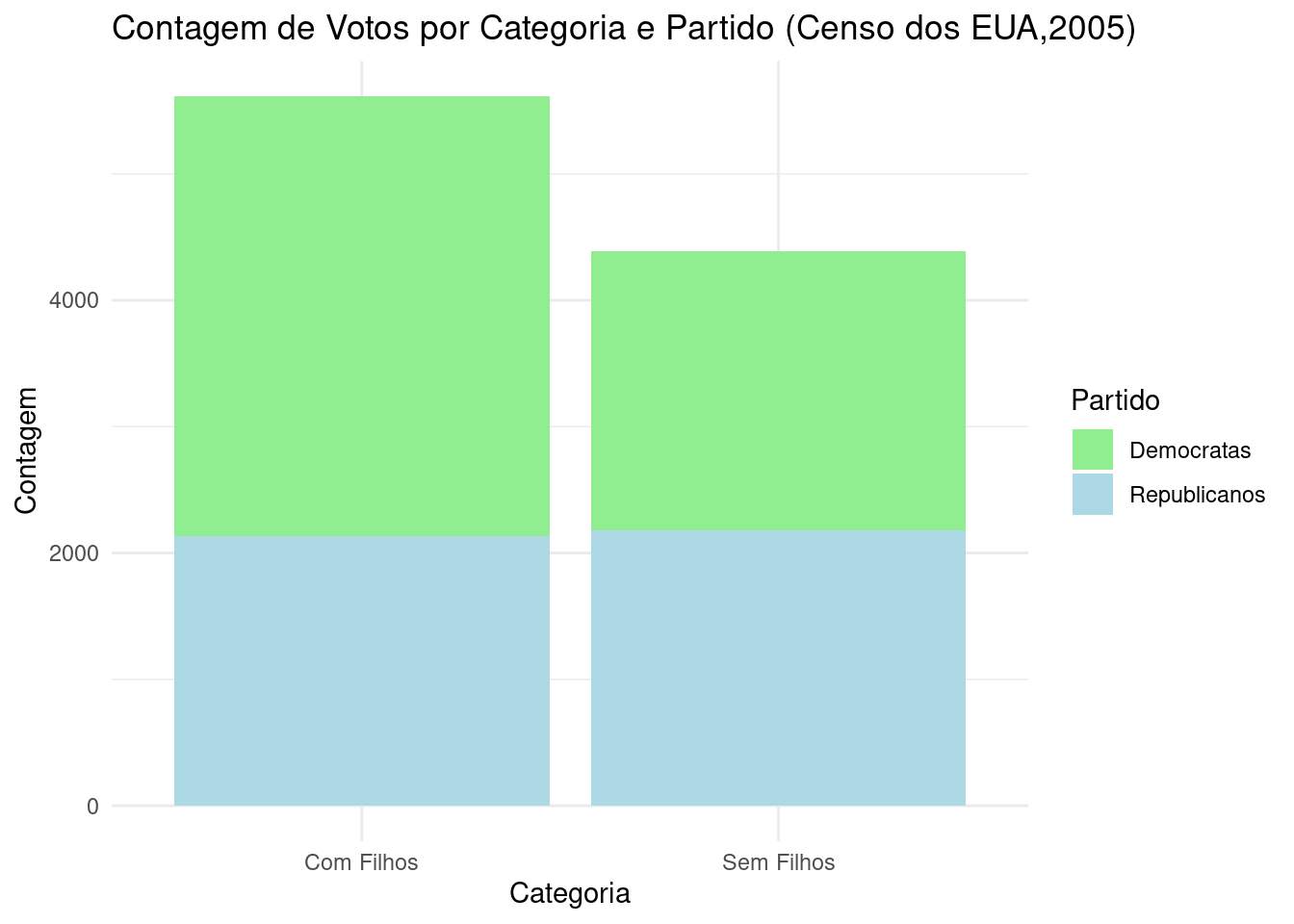

Figure 3.20: Gráfico de barras dos dados brutos: uma barra para cada observação e sua altura expressando o número de observações com esse valor

3.6.2.2 Histograma

Para dados quantitativos, o agrupamento dos valores brutos observados em classes (cada uma com um valor mínimo e máximo fixado) permite a geração de um Histograma, um tipo diferente de Gráfico de barras onde cada coluna está unida às colunas imediatamente adjacentes (indicando a continuidade de valores das medidas) e sua altura expressa a quantidade de observações contidas nessa classe.

Para as classes estabelecias na seção anterior o histograma das alturas dos estudantes terá esse aspecto:

h1=hist(alturas, breaks=seq(1.41 , 2.01 , 0.1),  include.lowest = TRUE, right = FALSE, main= "Histograma das alturas dos estudantes", col="blue", 
xlab="Classes de alturas (m)", ylab="Frequência absoluta observada (un)" , cex=0.7, ylim=c(0,30))
text(h1$mids,h1$counts,labels=h1$counts, adj=c(0.5, -0.5))
abline(v=mean(alturas), col="red") 
text(mean(alturas)-0.01, 28, "Média=1,69 m", col = "red", srt=90)
abline(v=median(alturas), col="darkgreen") 
text(median(alturas)-0.01, 27.2, "Mediana=1,675 m", col = "darkgreen", srt=90)
abline(v=Modes(alturas), col="darkgrey") 
text(Modes(alturas)+c(-0.01, -0.01), 27, c("Moda=1,66","Moda=1,73"), col = "darkgray", srt=90)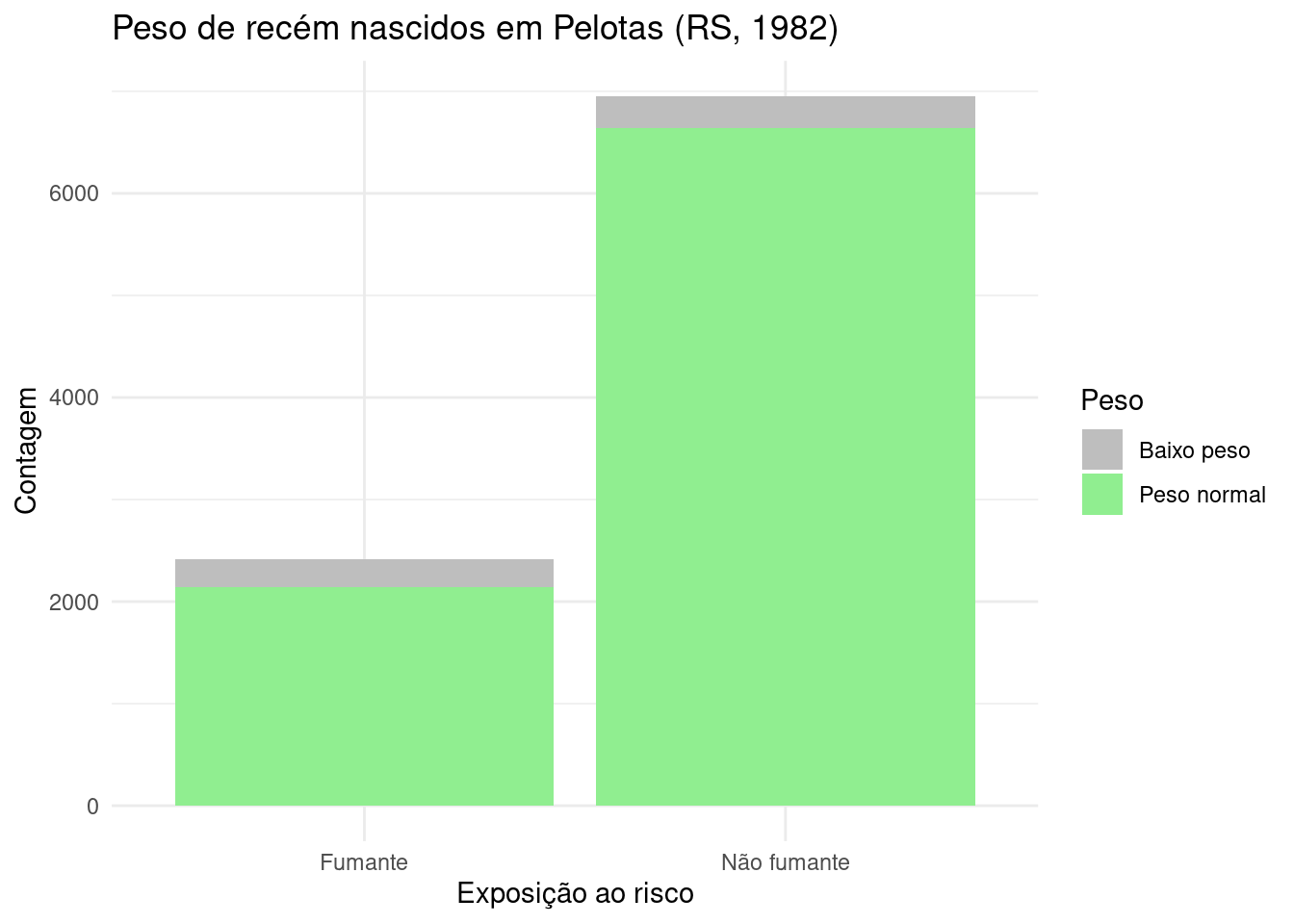

Figure 3.21: Histograma das alturas dos estudantes com as posições da média, moda e mediana

Um histograma é a representação gráfica de uma tabela de distribuição de frequências em colunas (retângulos).

A base de cada retângulo representa o intervalo de cada classe e a altura, a quantidade ou a frequência absoluta com que aquele valor da classe ocorre no conjunto de dados.

O termo histograma foi cunhado por Karl Pearson (c. 1891) e vem da composição em grego de istos (mastro) com gramma (escrita), convertida em inglês para historical diagram: histogram.

Como elemento gráfico, seu uso é anterior à sua denominação (maiores detalhes em: (link) ).

Num histograma de densidade, a altura de cada retângulo representa uma densidade relacionada à frequência relativa no intervalo de cada classe.

h2=hist(alturas,breaks=seq(1.41 , 2.01 , 0.10),  include.lowest = TRUE, right = FALSE, main= "Histograma das densidades das alturas dos estudantes", col="blue", 
xlab="Classes de alturas (m)", ylab="Densidade da freq. relativa", prob="TRUE", ylim=c(0,5))
text(h2$mids,h2$density,labels=round(h2$density, 5), adj=c(0.5, -0.5), cex=0.7)
lines(density(alturas), col="red")             
lines(density(alturas, adjust=2), col="orange")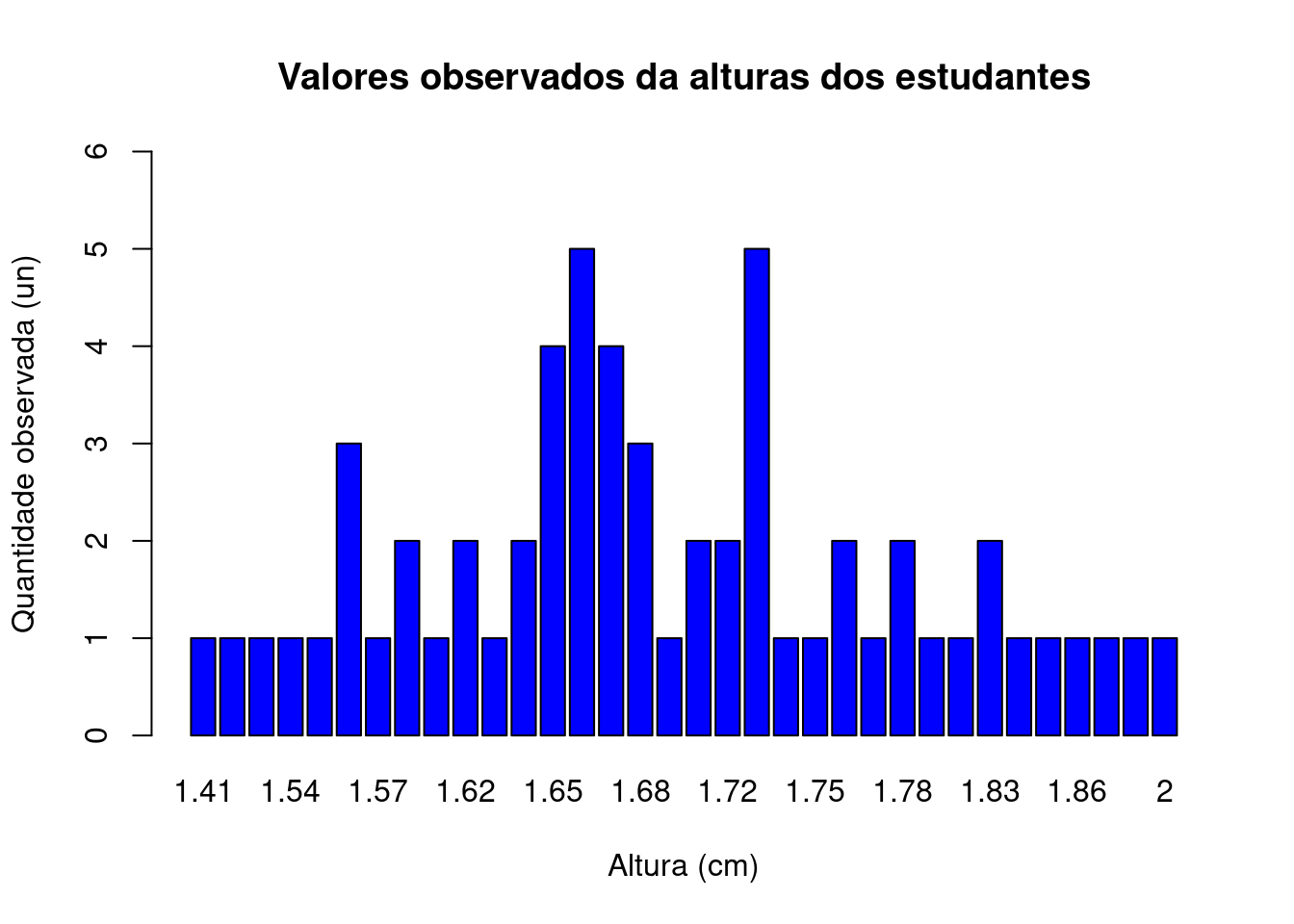  

Figure 3.22: A linha vermelha é uma aproximação da Função de Densidade da frequência relativa de observação (a linha preta é a curva da função densidade de uma distribuição Normal com média e variâncias dadas pelos dados

Como a área de cada retângulo é igual à proporção (\(fr_{i}\)) da classe (\(i\)) a soma de todas essas áreas será igual a 1:

(0.10*0.5)+(0.10*1.333)+(0.10*3.833)+(0.10*2.833)+(0.10*1)+(0.10*0.50)

## [1] 0.9999

Uma aproximação para a área sob a curva da Função de Densidade pode ser soma das áreas de um dos retângulo com:

• Base = \(\Delta_{i}\); e,\
• Altura =\(\frac{fr_{i}}{\Delta_{i}}\).

A área da curva da Função de Densidade delimitada por dois valores quaisquer é uma analogia para a probabilidade de que um determinado valor de altura de um estudante (amostrado aleatoriamente dentre todos os 60 estudantes) esteja contida nesse intervalo.

Equivale dizer que, amostrando-se aleatoriamente um estudante dentre todos os 60 alunos, a probabilidade de que a altura desse estudante estaje contida entre os valores mínimo e máximo da amostra é, naturalmente, igual a 1 (100%)

3.6.2.3 Setores

Em um Gráfico de setores a representação das quantidades está associada a uma fração do comprimento de um círculo. Para sua confecção considera-se a proporção da quantidade observada específica da quantidade total de dados, expressa na forma de fração do ângulo de um setor circular em relação ao ângulo interno total de um círculo (360^o).

library(scales)
library(ggplot2)

alturas_classes=data.frame(
  group = c("1,41-1,51",
            "1,51-1,61",
            "1,61-1,71",
            "1,71-1,81",
            "1,81-1,91",
            "1,91-2,01"),
  value = c(3,8,23,17,6,3))

blank_theme=theme_minimal()+
  theme(
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    panel.border = element_blank(),
    panel.grid=element_blank(),
    axis.ticks = element_blank(),
    plot.title=element_text(size=14, face="bold")
  )

ggplot(alturas_classes, aes(x="", y=value, fill=group)) +
  blank_theme +
  scale_fill_brewer("Blues")+
  ggtitle("Alturas dos estudantes") +
  theme(axis.text.x=element_blank()) +
  geom_bar(width = 1, stat = "identity") +
  coord_polar("y", start=0) +
  geom_text(aes(y = value/2 + c(0, cumsum(value)[-length(value)]),
                label = percent(value/60 )), size=5)+
  guides(fill = guide_legend("Classes de valores (m)",
                             label.position = "right",
                             title.position = "top", title.vjust = 1))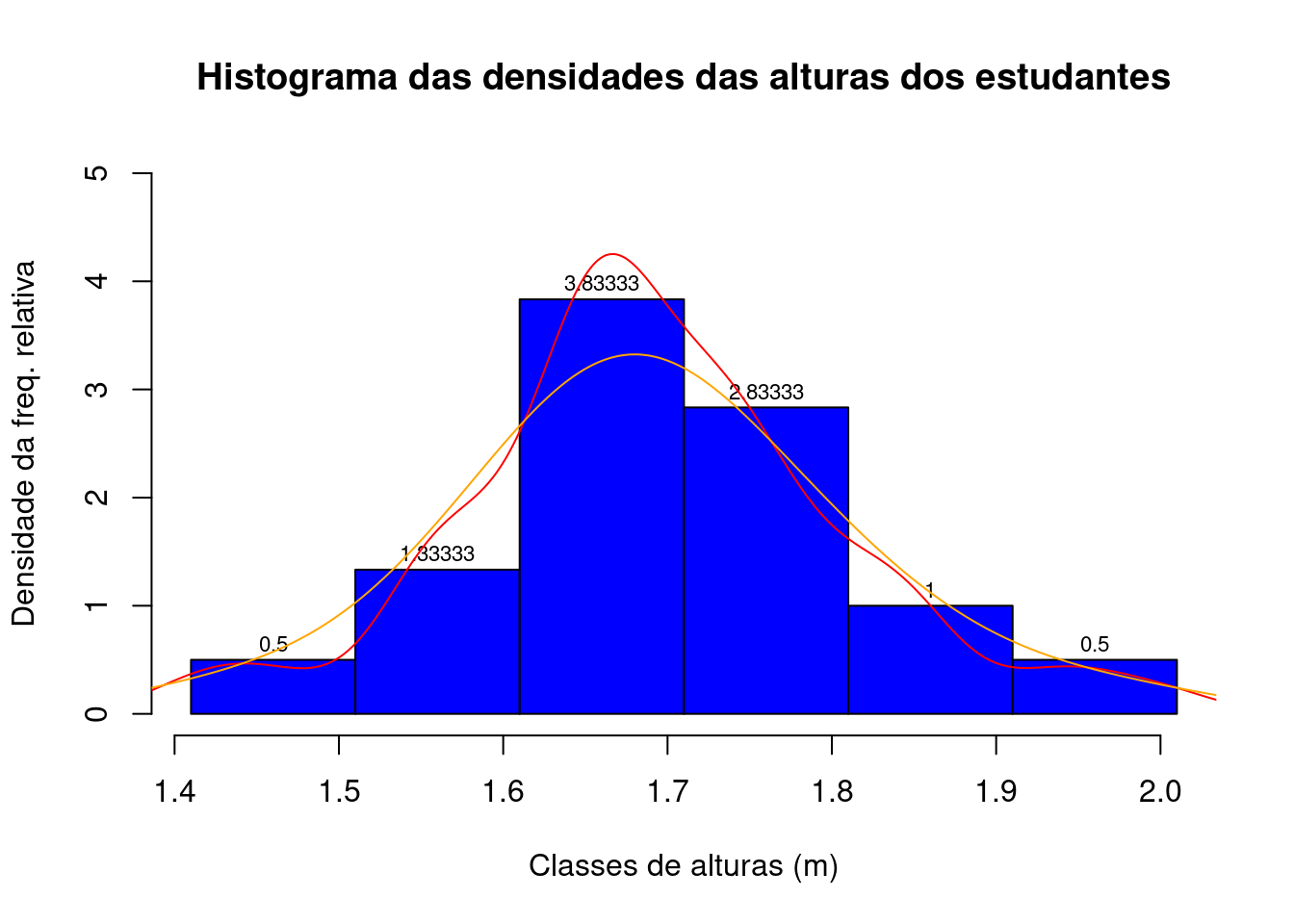 

Figure 3.23: Gráfico de setores das alturas dos estudantes

3.6.2.4 Box-plot (gráfico de caixas)

O gráfico Box-plot ( box and whisker plot ): esse gráfico apresenta de modo conjunto, informações sobre a posição, dispersão, assimetria e dados discrepantes do conjunto analisado:

• a mediana (\(Q_{2}\));
• os valores mínimo: \(x_{1}\) e máximo: \(x_{n}\) (dados ordenados);
• o 1\(^{o}\) e 3\(^{o}\) quartis;
• a dispersão (intervalo interquartílico: \(d_{q}=(Q_{3} - Q_{1})\));
• os limites superior: \(LS=Q_{3} + 1,50.d_{q}\), e inferior: \(LI=Q_{1} - 1,50.d_{q}\) ( bigodes);
• os valores mínimo e máximo observados (caso não existam valores superiores aos limites LI e LS); ou
• as observações mais extremas, situadas fora dos limites LI e LS (que podem ou não ser outliers , dados atípicos).

min=min(alturas)
q1=1.635
q2=1.675
med=mean(alturas)
q3=1.755
max=max(alturas)
iq=q3-q1
ls=q3+1.5*iq
li=q1-1.5*iq
head(sort(alturas,TRUE)) #2.00 1.95 >>1.93<< 1.86 1.85 1.84

## [1] 2.00 1.95 1.93 1.86 1.85 1.84

tail(sort(alturas,TRUE)) # 1.56 1.55 1.54 1.47 1.44 >>1.41<<

## [1] 1.56 1.55 1.54 1.47 1.44 1.41

boxplot(alturas, 
        main="Boxplot do conjunto de dados de alturas",
        ylim=c(1.2, 2.1))

lines( y=c(1.47, 1.47), x=c(0.6,1), col="blue") 
text(x=0.60, y=1.47-0.05, "Delimitador inferior do bigode=1,47", col = "blue", srt=0)

lines( y=c(1.93,1.93), x=c(0.6,1), col="blue") 
text(x=0.60, y=1.93+0.05, "Delimitador superior do bigode=1,93", col = "blue", srt=0)

lines(y=c(med, med),  x=c(1,1.4), col="blue") 
text(x=1.4 , y= med+0.05 , "Média=1,6907", col = "blue", srt=0)

lines(y=c(q1, q1), x=c(1, 1.4), col="blue") 
text(x=1.4, y=q1 -0.05, "Primeiro quartil: Q1=1,635", col = "blue", srt=0)

lines(y=c(q2, q2),  x=c(0.6,1), col="blue") 
text(x=0.60 , y= q2 - 0.05, "Mediana: Q2=1,675", col = "blue", srt=0)

lines(y=c(q3, q3), x=c(1, 1.4), col="blue") 
text(x= 1.4 , y=q3 + 0.05, "Terceiro quartil: Q3=1,755", col = "blue", srt=0)

lines(y=c(li,li) , x=c(1.01,1.4) , col="red", lty=2) 
text(x=1.2, y=q1-1.5*iq-0.05 , "Limite inferior teórico: LI=1,455) ", col = "red", srt=0)

lines(y=c(ls,ls) , x=c(1.01,1.4) , col="red", lty=2) 
text(x=1.2, y=q3+1.5*iq +0.05 , "Limite superior teórico: LS=1,935", col = "red", srt=0)

points (y=1.47, x=1 , col="green", cex=1, lwd=5) 
text(x=1, y=1.47-0.05 , "Última observação dentro do LI: h=1,47 ", col = "green", srt=0)

points (y=1.93, x=1 , col="green", cex=1, lwd=5) 
text(x=1, y=1.93+0.05 , "Última observação dentro do LS: h=1,93 ", col = "green", srt=0)

Figure 3.24: Box-plot de um rol de valores com Distribuição Normal (média 20 e variãncia 5