6.1 Modelos teóricos discretos
6.1.1 Uniforme
Variável aleatória \(X\), assumindo valores \(x_{1}, x_{2} , \dots, x_{k}\) tem distribuição uniforme se, e somente se,
\[ P(X=x_{i})=\frac{1}{k}. \] para todo \(i=1, 2, \dots, k\). Para uma variável com distribuição uniforme:
- Esperança: \(E(X)=\frac{1}{k}\sum_{i=1}^{k} x_{i}\)
- Variância: \(VAR(X)=\frac{1}{k} \left[ \sum_{i=1} ^{k} x_{i}^{2}\times\frac{( \sum_{i=1} ^{k} x_{i})^2}{k} \right]\)
6.1.2 Bernoulli
Variável aleatória com distribuição Bernoulli é uma variável definida por um experimento probabilístico em que os resultados possíveis se resumem a apenas dois: sucesso ou fracasso (ocorrência ou não).
Caracterização de uma variável aleatória \(X\) com distribuição de Bernoulli: \(X\sim Ber(p)\)
| xi | Evento | P(X = xi) |
|---|---|---|
| 1 | Sucesso | p |
| 0 | Fracasso | q=(1-p) |
| Σ | - | 1 |
Para uma variável de Bernoulli:
- Esperança: \(E(X)=p\)
- Variância: \(VAR(X)=p(1-p)\)
Exemplo: Seja \(X\) uma variável aleatória resultante do lançamento de um dado uma única vez e cujo sucesso está definido como obter a face com 5 pontos. Calcule a probabilidade de sucesso e fracasso, assim como sua variância.
| xi | Evento | P(X = xi) |
| (face 5 no lançamento de um dado) | ||
| 1 | Sucesso | p=1/6 |
| 0 | Fracasso | q=5/6 |
| Σ | - | 1 |
- Esperança: \(E(X)= \frac{1}{6}\)
- Variância: \(Var(X)= \frac{5}{36}\)
Admita agora \(X\) uma variável aleatória resultante de realização de \(n\) tentativas (repetições) de Bernoulli e definindo \(x\) como sendo o número de sucessos verificados nessas \(n\) tentativas. Desse modo, proporção de sucessos observada após \(n\) repetições é expressa como \(\frac{x}{n}\).
Se \(p\) é a probabilidade de sucesso a cada repetição e se \(\epsilon\) é um número qualquer positivo, tem-se:
\[
\underset{n\to \infty }{lim}P\left(\left|\frac{x}{n}-p\right|\ge \epsilon \right)=0
\]
A Lei dos grandes números para infinitas repetições de Bernoulli afirma que, após um grande número de repetições (\(n\)), a proporção de sucessos observada (\(\frac{x}{n}\)) irá se aproximar da probabilidade teórica da variável aleatória de Bernoulli \(p\).
6.1.3 Binomial
Variável aleatória com distribuição Binomial é uma variável resultante da repetição de um experimento modelado por uma variável de Bernoulli (isto é, a cada repetição apenas dois resultados podem ocorrer: sucesso ou fracasso).
Para que \(X\) seja uma variável aleatória com distribuição Binomial: \(X\sim b(n,p)\) é necessário que:
- o experimento deve ser realizado um número \(n\) finito de vezes;
- cada repetição deve ser independente das demais;
- cada repetição é, em essência, um ensaio de Bernoulli onde só pode haver dois resultados: sucesso ou fracasso;
- a probabilidade de sucesso \(p\) em cada repetição é sempre a mesma; e, consequentemente,
- a probabilidade de fracasso \(q=1-p\) em cada repetição é também a mesma.
Considerem o diagrama de árvore ilustrado na Figura 6.1 que representa, esquematicamente, 3 repetições independentes de um evento modelado por uma variável de Bernoulli, com probabilidade individual de sucesso \(P(X=1)=p\) e, de fracasso, \(P(X=0)=1-p=q\).
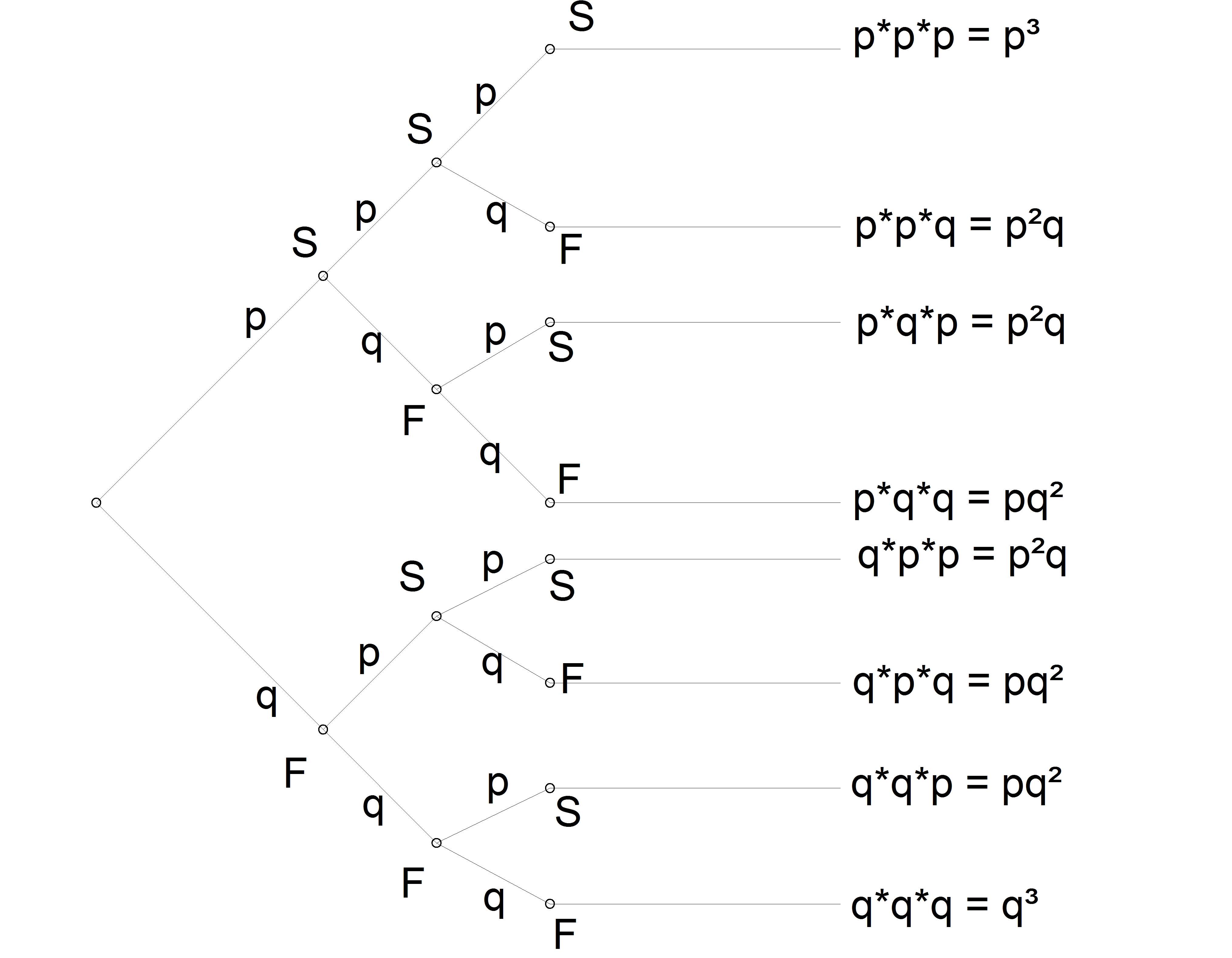
Figure 6.1: Três repetições independentes de um experimento aleatório modelado por uma variável de Bernoulli
Se \(p\) é a probabilidade de se verificar sucesso em qualquer uma das \(n\) repetições de Bernoulli realizadas no experimento aletório então uma variável aleatória Binomial \(X\) definida sobre esse experimento apresentará \(k\) sucessos após \(n\) repetições independentes e terá a seguinte função de probabilidade:
\[\begin{align*} f(k) & = P(X=k) \\ f(k) & = {C}_{k}^{n}. {p}^{k}. {q}^{(n-k)} \\ f(k) & = \frac{n!}{k!. (n-k)!} . {p}^{k}. {q}^{(n-k)} \end{align*}\]
Sendo a probabilidade \(p\) de sucesso, igual em todas as repetições, então:
- Esperança: \(E\left(X\right)=\sum _{i=1}^{n}{x}_{i}. P\left(X={x}_{i}\right)=n. p\)
- Variância: \(V\left(X\right)=E\left({X}^{2}\right)-{\left[E\left(X\right)\right]}^{2} = n . p . q\)
Exemplo: Numa prova com 6 questões, a probabilidade de que um aluno acerte cada uma delas é de 0,30. Admitindo que a resolução dessas 6 questões é feita de modo independente, qual a probabilidade desse aluno acertar 4 questões?
1- cada questão apresenta apenas duas possibilidades: acertar ou errar; assim, esse experimento aleatório pode seguir o modelo teórico de Bernoulli tendo o evento de sucesso definido como: a chance de acertar uma prova, com probabilidade de ocorrência \(p=0,30\);
2- ao se repetir esse experimento \(n=6\) (pois este é o número de questões a serem resolvidas) o experimento passa seguir o modelo teórico Binomial pois nos foi assegurada a independência entre cada repetição bem como a constância da probabilidade \(p\).
A probabilidade de se acertar \(k=4\) questões em \(n-6\) repetições independentes tendo cada uma uma probabilidade de sucesso \(p=0,30\) será então:
\[\begin{align*} P\left(X=k\right) & = {C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=4\right) & = 15 . 0,30^{4} . 0,70^{(6-4)} \\ & = 0,0595 \end{align*}\]
Conclusão: a probabilidade de um aluno acertar 4 questões das 6 resolvidas, considerando a probabilidade associada ao acerto de cada questão, é de 0,0595.
Exemplo: Ainda utilizando a construção teórica desse experimento, admitamos que nosso interesse reside em obter as seguintes probabilidades a ele associadas: 1- probabilidade do aluno não acertar nenhuma questão;
2- probabilidade do aluno acertar todas as questões;
3- probabilidade do aluno acertar no mínimo 2 questões; e a
4- probabilidade do aluno acertar no máximo 2 questões.
A resposta aos dois primeiros itens é imediata pela simples aplicação dos dados ao odelo, pois o número de sucessos desejado é \(k=0\) no primeiro e \(k=6\) no segundo (e \(p=0,30\) para todos) . Assim:
\[\begin{align*} P\left(X=k\right) & ={C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=0\right) & = 1 . 0,30^{0} . 0,70^{(6-0)} \\ & = 0,1176 \end{align*}\]
\[\begin{align*} P\left(X=k\right) & ={C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=6\right) & = 1 . 0,30^{6} . 0,70^{(6-6)} \\ & = 0,000729 \end{align*}\]
A resposta aos dois últimos itens irá demandar o uso da regra da adição de probabilidades e, como cada evento é disjunto dos demais, essa regra recai sobre a simples adição das probabilidades envolvidas.
Ao perguntar qual a probabilidade do aluno acertar no mínimo 2 questões (\(P(X \ge 2)\)) equivale a se perguntar qual a probabilidade do aluno acertar 2 OU 3 OU 4 OU 5 OU 6 questões. Assim, temos como elementos desses eventos de sucesso \({2, 3, 4, 5, 6}\). Assim a solução passará pelo cálculo das probabilidades individuais para cada um desses eventos de sucesso que serão simplesmente somadas pois, a ocorrência de cada um desses eventos de sucesso é disjunta dos demais (se ocorrer 2 não ocorre simultaneamente 3).
\[\begin{align*} P\left(X=k\right) & ={C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=2\right) & = 15 . 0,30^{2} . 0,70^{(6-2)} \\ & = 0,3241 \end{align*}\]
\[\begin{align*} P\left(X=k\right) & ={C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=3\right) & = 20 . 0,30^{3} . 0,70^{(6-3)} \\ & = 0,1852 \end{align*}\]
\[\begin{align*} P\left(X=k\right) & ={C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=4\right) & = 15 . 0,30^{4} . 0,70^{(6-4)} \\ & = 0,0595 \end{align*}\]
\[\begin{align*} P\left(X=k\right) & ={C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=5\right) & = 6 . 0,30^{5} . 0,70^{(6-5)} \\ & = 0,01020 \end{align*}\]
\[\begin{align*} P\left(X=k\right) & ={C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=6\right) & = 1 . 0,30^{6} . 0,70^{(6-6)} \\ & = 0,000729 \end{align*}\]
Assim, \(P\left(X\ge2\right)=0,3241+0,1852+0,0595+0,01020+0,00079=0,5797\)
# Defina o número de repetições (n) e o número de sucessos (k)
n=6 # Número de repetições
k=c(0,1,2,3,4,5,6) # Número de sucessos varia de nenhum (0) até dez (10) acertar as dez questões
p=0.30 # A probabilidade em cada repetição de Bernoulli
# Probabilidade de k sucessos em n repetições (utilizando a função 'dbinom')
probabilidade <- dbinom(k, n, prob = p) # Neste exemplo, 0.5 é a probabilidade de sucesso
# Crie uma tabela com duas colunas (Número de Sucessos e Probabilidade)
tabela <- data.frame(Número_de_Sucessos = k, Probabilidade = probabilidade)
# Exiba a tabela
print(tabela)## Número_de_Sucessos Probabilidade
## 1 0 0.117649
## 2 1 0.302526
## 3 2 0.324135
## 4 3 0.185220
## 5 4 0.059535
## 6 5 0.010206
## 7 6 0.000729
Exemplo: Uma pessoa trabalha em 3 empregos onde desenvolve atividades iguais, sendo remunerada também igualmente nos três lugares. A probabilidade de que o pagamento saia até o 2\(^{o}\) dia útil nos três empregos é de 0,85. Qual a probabilidade de apenas um salário sair até o 2\(^{o}\) dia útil?
1- a probabilidade de ocorrência do pagamento até o 2\(^{o}\) dia útil em cada emprego pode ser modelada por uma variável aleatória de Bernoulli pois apresenta apenas duas possibilidades: ocorrer ou não, cuja probabilidade de sucesso nos foi dada: \(p=0,85\);
2- os três empregos podem ser considerados como repetições desse experimento básico;
3- esse experimento final pode ter as probabilidades modeladas por uma variável aleatória Binomial com evento de sucesso definido como chance de se receber apenas um pagamento até o 2\(^{o}\) dia útil (\(k=1\)) pois consiste na repetição de (\(n=3\)) experimentos de Bernoulli independentes e com probabilidade individual constante (\(p-0,85\)).
A probabilidade de se receber o pagamento até o 2\(^{o}\) dia útil em apenas um emprego será dada por:
\[\begin{align*} P\left(X=k\right) & ={C}_{k}^{n}. {p}^{k}. {q}^{n-k} \\ P\left(X=1\right) & =3 . 0,85^{1} . 0,15^{2} \\ & = 0,0574 \end{align*}\]
Conclusão: a probabilidade desse trabalhador receber apenas um salário até o 2\(^{o}\) dia útil do mês é de 0,0574.
# Defina o número de repetições (n) e o número de sucessos (k)
n=3 # Número de repetições
k=c(0,1,2,3) # Número de sucessos varia de nenhum (0) até três (3) receber até o segundo dia nos três empregos
p=0.85 # A probabilidade em cada repetição de Bernoulli
# Probabilidade de k sucessos em n repetições (utilizando a função 'dbinom')
probabilidade = dbinom(k, n, prob = p) # Neste exemplo, 0,856 é a probabilidade de sucesso
# Crie uma tabela com duas colunas (Número de Sucessos e Probabilidade)
tabela = data.frame(Número_de_Sucessos = k, Probabilidade = probabilidade)
# Exiba a tabela
print(tabela)## Número_de_Sucessos Probabilidade
## 1 0 0.003375
## 2 1 0.057375
## 3 2 0.325125
## 4 3 0.614125
6.1.4 Poisson
A distribuição de Poisson (assim chamada em homenagem a Siméon Denis Poisson que a descobriu no início do século XIX) é largamente empregada quando se deseja contar o número de eventos raros cuja probabilidade média seja dada em termos de um intervalo de tempo, determinada extensão, área ou volume (uma taxa).
Uma variável aleatória discreta \(X\) com Distribuição de Poisson é aquela que pode assumir infinitos valores numeráveis (\(k=0,1,2, .s, \infty\)). Sua representação é: \(X \sim Pois (\lambda)\) e sua função de probabilidade para esses valores é:
\[\begin{align*} f(k) & = P(X=k) \\ & = \frac{\lambda^{k}. \epsilon^{-\lambda}} {k!} \end{align*}\]
Com \(\epsilon= 2,718\) (número irracional de Euler).
A esperança e a variância de uma variável aleatória discreta com Distribuição de Poisson são dados pelo seu parâmetro \(\lambda\) que expressa o número médio de eventos ocorrendo no intervalo de tempo, ou em uma determinada extensão, área ou volume :
- Esperança: \(E(X) = \lambda\);
- Variância: \(Var(X) = \lambda\)
Exemplo:Uma central telefônica recebe em média 5 chamadas por minuto. Supondo que a Distribuição de Poisson seja adequada a esse contexto, obter as probabilidade de que essa central não receba chamadas num intervalo de 1 e que receba no máximo duas chamadas em 4 minutos.
Dados do problema:
1- \(\lambda=\) é o parãmetro da distribuição de Poisson (a esperança, a média); assim temos \(\lambda=5\) chamadas por minuto (é importante atentar para qual é a unidade associada ao valor do \(\lambda\));
2- não receber chamada alguma equivale a um \(k=0\);
3- na sequência, ao se perguntar sobre a probabilidade de se receber no máximo duas chamadas em 4 minutos equivale a não receber chamada alguma ou uma chamada ou duas chamadas (soma das probabilidades de eventos mutuamente excludentes);
4- mas é necessário reestimar o valor de \(\lambda\) pois agora o intervalo de tempo é de 4 minutos e o valor que nos foi dado é para 1 minuto (o que é feito mediante uma simples regra de três: 5 chamadas em um minuto passam a ser 20 chamadas em quatro minutos)
Probabilidade de não receber chamada alguma:
\[\begin{align*} P(X=k) & = \frac{\lambda ^{k}. \epsilon^{-\lambda}} {k!} \\ P(X=0) & = \frac{5^{0}. \epsilon^{-5}} {0!} \\ P(X=0) & = \frac{1 . 0,00673}{1}\\ & = 0,00673 \end{align*}\]
Probabilidade de receber no máximo 2 chamadas em 4 minutos (\(\lambda = 20\) chamadas por 4 minutos):
\[\begin{align*} P(X=0) & = \frac{20^{0}. \epsilon^{-20}} {0!} = 2,061154e-09 \\ P(X=1) & = \frac{20^{1}. \epsilon^{-20}} {1!} = 4,122307e-08 \\ P(X=2) & = \frac{20^{2}. \epsilon^{-20}} {2!} = 4,122307e-07 \\ \end{align*}\]
\(P(X \le 2)=P(X=0)+P(X=1)+P(X=2)=4,554699e-7\)
# Defina o número de repetições (n) e o número de sucessos (k)
k= 0 # Número de sucessos varia de nenhum (0) até infinito
l= 5 # A probabilidade de sucesso na proporção dada (área, comprimento, tempo...) 5 chamadas por minuto
k1= c(0,1,2)
l1= 20 # 5 chamadas em 1 minuto >> 20 chamadas em 20 minutos
# Probabilidade de k sucessos em n repetições (utilizando a função 'dbinom')
probabilidade = dpois(k, lambda = l) # Neste exemplo, l=5 chamadas por minuto
probabilidade1 = dpois(k1, lambda = l1) # Neste exemplo, l=20 chamadas por minuto
# Crie uma tabela com duas colunas (Número de Sucessos e Probabilidade)
tabela = data.frame(Número_de_Sucessos = k, Probabilidade = probabilidade)
tabela1 = data.frame(Número_de_Sucessos = k1, Probabilidade = probabilidade1)
# Exiba a tabela
print(tabela)## Número_de_Sucessos Probabilidade
## 1 0 0.006737947## Número_de_Sucessos Probabilidade
## 1 0 2.061154e-09
## 2 1 4.122307e-08
## 3 2 4.122307e-07
Exemplo: Um posto de bombeiros recebe em média 3 chamadas por dia. Admitindo que as probabilidades associadas ao recebimento de diferentes números de chamadas podem ser modeladas por uma variável aleatória de Poisson qual seria a probabilidade desse posto receber 4 chamadas em 2 dias?
A unidade da esperança dessa variável de Poisson (\(\lambda\)) de chamadas nos foi dada por dia ao passo que a probabilidade pedida está associada a um período de dois dias, exigindo que a esperança \(\lambda\) seja convertida para essa nova unidade (uma simples regra de três: 3 chamadas por dia, então para 2 dias, 6 chamadas). Assim, a probabilidade pedida será:
\[\begin{align*} P(X=k) & = \frac{\lambda ^{k}. \epsilon^{-\lambda}} {k!}\\ P(X=4) & = \frac{6^{4}. \epsilon^{-6}} {4!} \\ & = 0,1338 \end{align*}\]
A figura abaixo ilustra a distribuição acumulada das probabilidades de alguns sucessos para o exemplo em estudo.
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.5.1
## ✔ lubridate 1.9.4 ✔ tibble 3.2.1
## ✔ purrr 1.0.4 ✔ tidyr 1.3.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ readr::col_factor() masks scales::col_factor()
## ✖ purrr::discard() masks scales::discard()
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::group_rows() masks kableExtra::group_rows()
## ✖ dplyr::lag() masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errorsprob=c(0.00248, 0.01448, 0.044643, 0.08929, 0.1338, 0.16072, 0.16072, 0.137762, 0.256105)
k=c("k=0", "k=1", "k=2", "k=3", "k=4", "k=5", "k=6", "k=7", "soma(k=8,k=9,...,inf)")
legend_title="Sucessos"
nchamadas=data.frame(sucesso = k, proporcao= prob)
nchamadas=nchamadas %>%
mutate(va_poisson = "Probabilidades segundo o modelo teórico de Poisson")
ggplot(nchamadas, aes(x = va_poisson, y =proporcao, fill = forcats::fct_rev(sucesso))) +
geom_col( width = 0.2) +
geom_text(aes(label = proporcao),size=3,
position = position_stack(vjust = 0.5) ) +
theme(legend.position = "right") +
ylab("Probabilidade acumulada") +
xlab(NULL)+
scale_fill_discrete(name="Número de sucessos",
labels=rev(c("k=0", "k=1","k=2","k=3","k=4",
"k=5","k=6","k=7","soma(k=8,k=9,...,inf)")))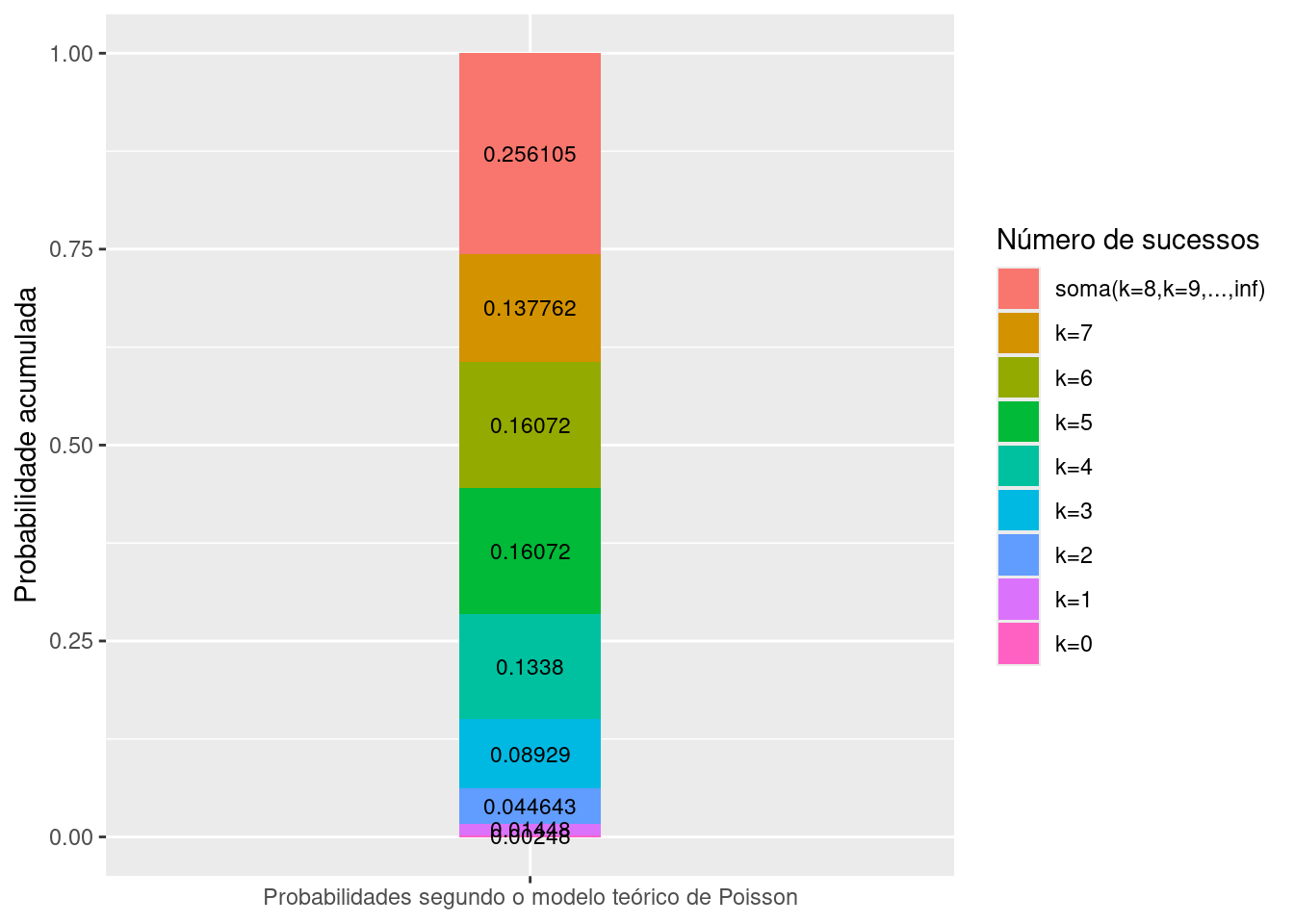
Figure 6.2: Gráfico ilustrativo das probabilidades acumuladas
Exemplo: Por um posto de pedágio passam, em média, 5 carros por minuto. Qual a probabilidade de passarem exatamente 3 carros em 1 minuto?
\[\begin{align*} P(X=k) & = \frac{\lambda ^{k}. \epsilon^{-\lambda}} {k!} \\ P(X=3) & = \frac{5^{3}. \epsilon^{-5}} {3!} \\ & = 0,1404 \end{align*}\]
Uma variável aleatória discreta de Poisson modela muito bem eventos raros; ou seja, aqueles que não acontecem com grande frequência para qualquer intervalo considerado (tempo, extensão, área, volume). Trata-se de uma caso de variável Binomial no qual \(n \to \infty\) e \(p\) é pequeno (\(n \ge 50\) e \(n . p \le (5)\)). Nesse cenário pode-se demonstrar que:
\[ lim_{n \to \infty} P(X) = {C}_{k}^{n}. {p}^{k}. {q}^{n-k} \]
é igual a:
\[ P(X=k) = \frac{\lambda ^{k}. \epsilon^{-\lambda}} {k!} \]
Tal aproximação era, tempos atrás (antes da era computacional), bastante útil pois, para um \(n\) muito grande o cálculo fatorial era trabalhoso! Nesse contexto pode-se modelar o experimento acima, de modo bem aproximado, por uma variável aleatória de Poisson com \(\lambda=n . p\):
\[ f(k) = P(X=k) = \frac{n . p^{k}. \epsilon^{- n . p}} {k!} \]
6.1.5 Multinomial
A distribuição multinomial é uma generalização da distribuição binomial - a qual admite apenas dois resultados: sucesso e fracasso - para as situações de mais de dois valores. Assim como a distribuição binomial, a distribuição multinomial é uma função de distribuição para processos discretos nos quais prevalecem probabilidades fixas para cada valor gerado de modo independente uns dos outros.
Admita que \(X\) seja uma variável aleatória com distribuição multinomial: \(X_{k} \sim multinomial(n , \boldsymbol{p})\) que envolve um processo aleatório que possui um conjunto de \(k\) possíveis resultados, cada um com sua probabilidade \(p_{k}\) definida:
\[ X_{k} = \begin{cases} X_{1} \text{ com probabilidade } p_{1} \\ X_{2} \text{ com probabilidade } p_{2} \\ \vdots \\ X_{k} \text{ com probabilidade } p_{k} \\ \end{cases} \]
- \(X_{1}, X_{2}, \dots, X_{k}\) são os \(k\) possíveis resultados assumidos pela variável aleatória multinomial \(X_{k}\) ;
- \(\boldsymbol{p}\) é o vetor de probabilidades \(p_{1}, p_{2}, \dots, p_{k}\) associadas à ocorrência de cada um dos possíveis resultados da variável aleatória multinomial \(X_{k}\);
- \(n\) é o número finito de vezes que o experimento é realizado;
- \(n_{1}, n_{2}, \dots, n_{k}\) é o número de sucessos observados em cada um dos possíveis resultados que a variável aleatória multinomial \(X_{k}\) pode assumir, de tal modo que \(n_{1} + n_{2} + \dots + n_{k} = n\);
- as probabilidades de sucesso \(p_{k}\) em cada uma das repetições são sempre as mesmas: indepenendência de resultados entre as as repetições.
A função de distribuição de probabilidades é dada por:
\[\begin{align*} f(X=(n_{1}, n_{2}, \dots, n_{k})) & = P(X_{1}=n_{1}; X_{2}=n_{2}, \dots, X_{k}=n_{k}) \\ P(X_{1}=n_{1}; X_{2}=n_{2}, \dots, X_{k}=n_{k}) & = \frac{n!}{n_1!n_2!\cdots n_{k}!}. p_1^{n_1} \cdot p_2^{n_2} \dots p_k^{n_k} \end{align*}\]
A esperança e a variância de uma variável aleatória discreta com Distribuição de multinomial são dadas por:
- O vetor esperança: \(E(X_{k}) = n.\boldsymbol{p}_{k} = \{n.p_{1};n.p_{2};\cdots;n.p_{k}; \}\);
- O vetor variância: \(Var(X_{k}) = n.\boldsymbol{p}_{k}.(1-\boldsymbol{p}_{k})= \{n.p_{1}.(1-p_{1});n.p_{2}.(1-p_{2});\cdots;n.p_{k}.(1-p_{k})\}\).
Os valores do vetor da esperança numericamente calculados poderão ser arredondados se o objetivo incluir sua aplicação prática em algum contexto; caso contrário, permanecem como calculados foram.
Exemplo: Em uma partida de xadrez dois jogadores têm a probabilidade de vencer, perder ou empatar. A probabilidade do jogador “A” vencer é 0,40, do jogador “B” vencer é 0,35 e do jogo terminar empatado é de 0,25. Calcule a probabilidade de em 12 partidas, observar-se que o jogador “A” ganhou 7 partidas, o jogador “B” venceu 2 partidas e as 3 partidas restantes terminaram em empate.
Uma variável aleatória \(X\) pode ser definda para modelar a probabilidade dos diferentes resultados possíveis nesse experimento aleatório tal que \(X_{3} \sim multinomial (n, \boldsymbol{p})\) tal que:
\[ X_{3} = \begin{cases} X_1\text{: "A" ganha } \text{probabilidade } p_{1}=0,40 \\ X_2\text{: "B" ganha } \text{probabilidade } p_{2}=0,35 \\ X_3\text{: empate entre "A" e "B"} \text{probabilidade } p_{3}=0,25 \\ \end{cases} \]
\[\begin{align*} P(X_{1}=n_{1};X_{2}=n_{2};X_{3}=n_{3}) & = \frac{n!}{n_1!n_2!n_{3}!} \cdot p_1^{n_1} \cdot p_2^{n_2} \cdot p_3^{n_3}\\ P(X_{1}=7;X_{2}=2;X_{3}=3) & = \frac{12!}{7!2!3!} \cdot 0,40^{7} \cdot 0,35^{2} \cdot 0,25^{3}\\ P(X_{1}=7;X_{2}=2;X_{3}=3) & = 0.02483712 \end{align*}\]
# Defina as probabilidades de sucsesso de cada possível resultado da variável aleatória: p_(k). Admita que existam apenas tês:
p1= 0.4
p2= 0.35
p3= 0.25
# O número de repetições 'n' é automaticamente definido pelo arranjo de sucessos que se deseja estimar a probabilidade
x=c(7,2,3) # Nesse caso deseja-se 7 sucessos do resultado X_1 (jogador 1), 2 do X_2 (jogador 2) e 3 do X_3 (jogador 3)
# Probabilidade desse vetor de sucessos (utilizando a função 'dmultinom')
probabilidade = dmultinom(x=c(7,2,3), prob = c(0.4,0.35,0.25))
print(probabilidade)## [1] 0.02483712