11.9 Teste de médias amostrais independentes de duas populações Normais

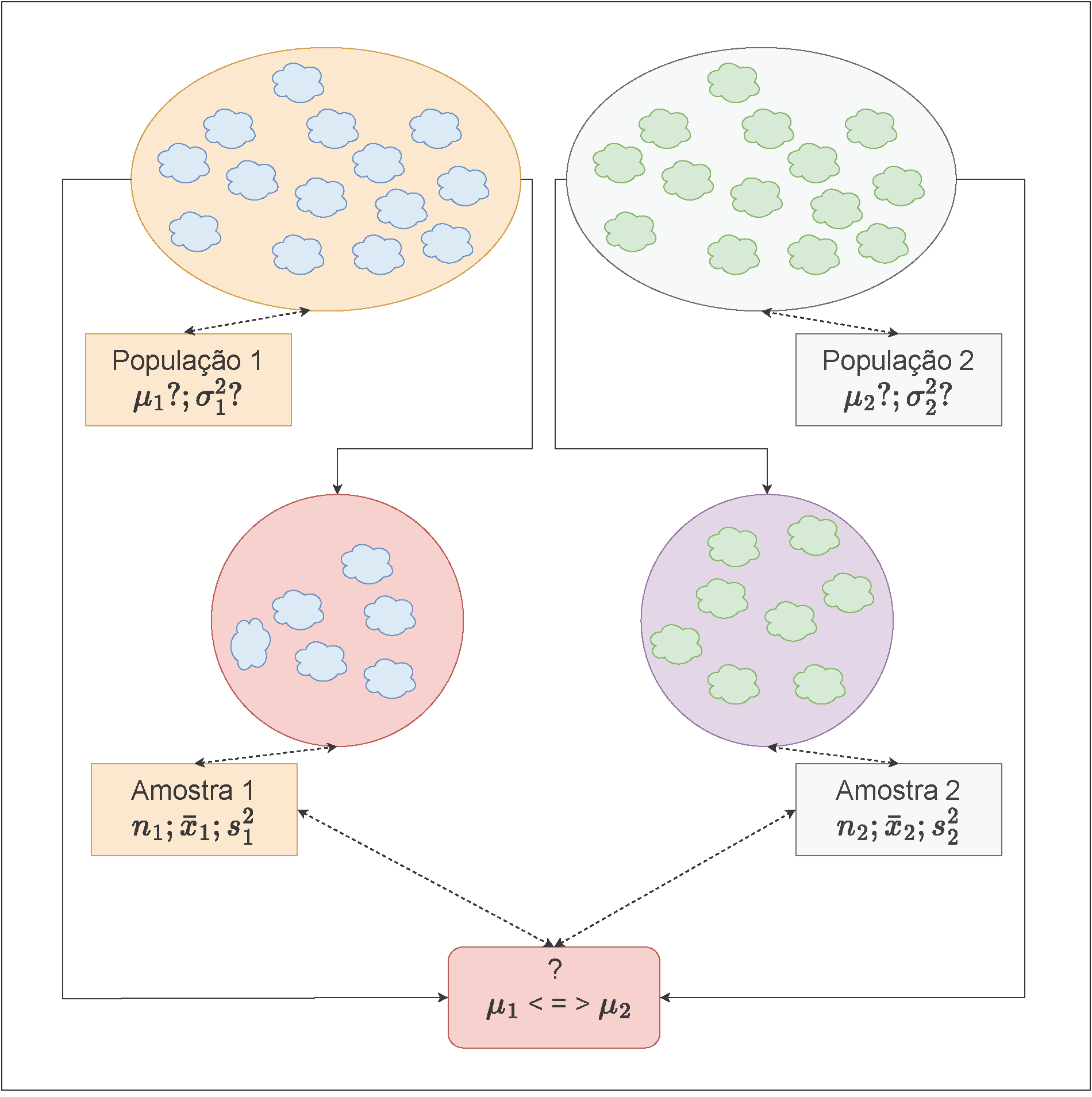
Figure 11.17: Visão esquemática das amostras de duas populações

Pelo Teorema Limite Central, para tamanhos amostrais \(n\) suficientemente grandes a média amostral \(\stackrel{-}{X}\) tem distribuição aproximadamente Normal, com média \(\mu\) e variância \(\frac{\sigma^{2}}{n}\), independente da distribuição da população, onde \(\mu\) e \(\sigma^{2}\) são a média e a variância populacionais.

• grandes: \(n \geq 30 (40)\); e
  
• pequenas: \(n < 30\).

Situações possíveis:

• Variâncias populacionais conhecidas ou não conhecidas mas com amostras de grande tamanho;
  
• Variâncias populacionais desconhecidas:
  • Variâncias populacionais admitidas iguais; ou,
    
  • Variâncias populacionais quaisquer.

Os valores assumidos pelas características de nosso interesse nas populações são tais que:

\[ X_{1} \sim \mathcal{N}(\mu_{1}; \sigma^{2}_{1}) \]

e

\[ X_{2} \sim \mathcal{N}(\mu_{2}; \sigma^{2}_{2}) \]

Ao se extrair duas amostras, os valores amostrais assumidos por essas características serão duas variáveis aleatórias tais que:

\[ \stackrel{-}{X}_{1} \sim \mathcal{N} (\mu_{1}\frac{\sigma^{2}_{1}}{n_{1}}) \]

e

\[ \stackrel{-}{X}_{2} \sim \mathcal{N} (\mu_{2};\frac{\sigma^{2}_{2}}{n_{2}}). \]

É de nosso particular interesse definir uma variável aleatória expressa como a diferença das variáveis \(\stackrel{-}{X}_{1}\) e \(\stackrel{-}{X}_{2}\).

Segue-se assim (por serem independentes) que

\[ \stackrel{-}{X}_{1}-\stackrel{-}{X}_{2} \sim \mathcal{N} (\mu_{1}-\mu_{2}; \frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}}) . \]

11.9.1 As estruturas possíveis dos testes de hipóteses relacionados às suas médias serão:

Teste bilateral (tipo: diferente de)

\[ \begin{cases} H_{0}:\mu_{1} - \mu_{2} = \Delta_{0} \\ H_{1}:\mu_{1} - \mu_{2} \ne \Delta_{0} \\ \end{cases} \]

Teste unilateral à esquerda (tipo: menor que)

\[ \begin{cases} H_{0}:\mu_{1} - \mu_{2} \ge \Delta_{0}\\ H_{1}: \mu_{1} - \mu_{2} < \Delta_{0}\\ \end{cases} \]

Teste unilateral à direita (tipo: maior que)

\[ \begin{cases} H_{0}:\mu_{1} - \mu_{2} \le \Delta_{0}\\ H_{1}: \mu_{1} - \mu_{2} > \Delta_{0}\\ \end{cases} \]

Os valores assumidos pelas diferenças amostrais são tais que:

\[ \frac{\stackrel{-}{X}_{1}-\stackrel{-}{X}_{2} - \Delta_{0}}{\sqrt{\frac{\sigma^{2}_{1}}{n_{1}} + \frac{\sigma^{2}_{2}}{n_{2}}}} \sim \mathcal{N} (0,1) \]

para

• amostras Normais: \(n_{1}\) e \(n_{2}\) qualquer;
  
• amostras sob outras distribuições, desde que: \(n_{1}\) e \(n_{2} \ge 30(40)\):
  
• \({Z}_{tab\left(\frac{\alpha }{2}\right)}\) ou \({Z}_{tab\left(\alpha \right)}\): valores da distribuição Normal padronizada para o nível de significância pretendido no teste (bilateral ou unilateral); e,
  
• \(Z_{calc} = \frac{(\stackrel{-}{x}_{1} - \stackrel{-}{x}_{2})-\Delta_{0}}{\sqrt{\frac{\sigma^{2}_{1}}{n_{1}}+\frac{\sigma^{2}_{2}}{n_{2}}}} \sim \mathcal{N}(0,1)\)

em que:

• \(\Delta_{0}\) é o valor inferido à diferença das médias populacionais \(\mu_{1}\) e \(\mu_{2}\), usualmente 0 (igualdade);
  
• \(\sigma_{1}^{2}\) é a variância da população 1;
  
• \(\sigma_{2}^{2}\) é a variância da população 2;
  
• \(\stackrel{-}{x}_{1}, n_{1}\) são a média e o tamanho da amostra 1; e,
  
• \(\stackrel{-}{x}_{2}, n_{2}\) são a média e o tamanho da amostra 2.

11.9.2 Testes de hipóteses para as médias de duas populações com variâncias conhecidas (ou não conhecidas mas o tamanho das amostras é grande)

Probabilidade dos intervalos de confiança para os testes de hipóteses com o uso da estatística Z (\(Z \sim \mathcal{N}(0,1)\)):

• Teste de hipóteses bilateral (tipo: diferente de):

\[\begin{align*} P[\left|Z_{calc}\right| \le {Z}_{tab\left(\frac{\alpha }{2}\right)}|\mu_{1}=\mu_{2}] & =(1-\alpha)\\ P(-{Z}_{tab\left(\frac{\alpha }{2}\right)} \le Z_{calc} \le {Z}_{tab\left(\frac{\alpha }{2}\right)}) & = (1-\alpha)\\ \end{align*}\]

• Teste de hipóteses unilateral à esquerda (tipo: menor que):

\[\begin{align*} P[Z_{calc} \ge -{Z}_{tab\left(\alpha \right)}|\mu_{1} \ge \mu_{2}] & =(1-\alpha) \\ P( Z_{calc} \ge -{Z}_{tab\left(\alpha \right)}) & = (1-\alpha) \\ \end{align*}\]

• Teste de hipóteses unilateral à direita (tipo maior que):

\[\begin{align*} P[Z_{calc} \le {Z}_{tab\left(\alpha \right)}|\mu_{1} \le \mu_{2}] & =(1-\alpha) \\ P( Z_{calc} \le {Z}_{tab\left(\alpha \right)}) & = (1-\alpha) \\ \end{align*}\]

Nas figuras 11.8, 11.9 e 11.10 observam-se:

 

• as regiões de rejeição da hipótese nula (subdivididas nos dois ou em apenas um dos lados) sob a curva da função densidade de probabilidade da distribuição adequada ao teste com probabilidades iguais ao nível de significância \(\alpha\) ;
  
• a região de não rejeição da hipótese nula (delimitada à esquerda e à direita ou apenas em um dos lados) com probabilidade igual ao nível de confiança \((1-\alpha)\); e,
  
• os valores críticos da estatística do teste.

Exemplo: Duas máquinas são usadas para encher garrafas plásticas com um volume líquido de 16oz. Os volumes de enchimento podem ser admitidos como normais, tendo desvios padrão iguais a \(\sigma_{1}=0,020\)oz e \(\sigma_{2}=0,025\)oz. O departamento de engenharia da fábrica deseja saber a um nível de significância de \(\alpha=0,01\) se ambas as máquinas enchem um mesmo volume e para isso coletou uma amostra de 10 garrafas enchidas por cada uma das máquinas cf. tabela abaixo:

Enchimento de duas máquinas

Máquina 01		Máquina 02
16,03	16,01	16,02	16,03
16,04	15,96	15,97	16,04
16,05	15,98	15,96	16,02
16,05	16,02	16,01	16,01
16,02	15,99	15,99	16,00

As variâncias populacionais \(\sigma_{1}^{2}\) e \(\sigma_{2}^{2}\) são conhecidas e as populações seguem uma distribuição Normal. A estatística do teste é:

\[ z_{calc} = \frac{(\stackrel{-}{x}_{1} - \stackrel{-}{x}_{2}) }{\sqrt{\frac{\sigma^{2}_{1}}{n_{1}}+\frac{\sigma^{2}_{2}}{n_{2}}}} \]

tal que tal que Z (\(Z \sim \mathcal{N}(0,1)\)), em que:

• \(\mu_{1} , \mu_{2}\) são as médias das populações em teste;
  
• \(\sigma_{1}^{2}=0,020^{2}, \sigma_{2}^{2}=0,025^{2}\) são as variâncias das populações em teste;
  
• \(\stackrel{-}{x}_{1}=16,015, n_{1}=10\) são a média e o tamanho da amostra 1;
  
• \(\stackrel{-}{x}_{2}=16,005, n_{2}=10\) são a média e o tamanho da amostra 2; e,
  
• o nível de significância estabelecido para o teste é \(\alpha=0,01\).

O problema nos pede um teste bilateral (tipo: diferente de):

\[ \begin{cases} H_{0}: \mu_{1} - \mu_{2} = 0 \\ H_{1}: \mu_{1} - \mu_{2} \ne 0 \\ \end{cases} \]

Se \(z_{calc}\) for tal que:

\[ -{z}_{tab\left(\frac{\alpha }{2}\right)} \le z_{calc} \le {z}_{tab\left(\frac{\alpha }{2}\right)} \]

não se rejeita a hipótese nula sob o nível de signficância estabelecido. Da tabela da distribuição Normal padronziada obtemos o valor crítico bicaudal: \(|{Z}_{tab\left(\frac{\alpha }{2}\right)}|=2,57\). Pelo cálculo, a estatística do teste é \(z_{calc}=0,98773\).

alfa=0.01

prob_desejada1=alfa/2
z_desejado1=round(qnorm(prob_desejada1),4)
d_desejada1=dnorm(z_desejado1, 0, 1)

prob_desejada2=1-alfa/2
z_desejado2=round(qnorm(prob_desejada2),4)
d_desejada2=dnorm(z_desejado2, 0, 1)

z_calculado=0.98773
d_calculado=dnorm(z_calculado, 0, 1)


ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de z", breaks = c(z_desejado1,z_desejado2))  +
  labs(title= 
         "Regiões críticas sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P(-2,57, 2,57)=(1-\u03b1) em cinza (nível de confiança=0,99) \nP(-\U221e; -2,57)= P(2,57; \U221e)= \u03b1/2 em vermelho (nível de significância/2=0,005) ")+
  geom_segment(aes(x = z_desejado1, y = 0, xend = z_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = z_desejado2, y = 0, xend = z_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_desejado1-0.1, y=d_desejada1, label="valor crítico=-2,57", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.3, y=d_desejada2, label="valor crítico=2,57", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1-1.5, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.5, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+2, y=0.2, label="Região de não rejeição da hipótese nula \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  geom_segment(aes(x = z_calculado, y = 0, xend = z_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_calculado-0.1, y=d_calculado, label="valor da estatística do teste=0,9877", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()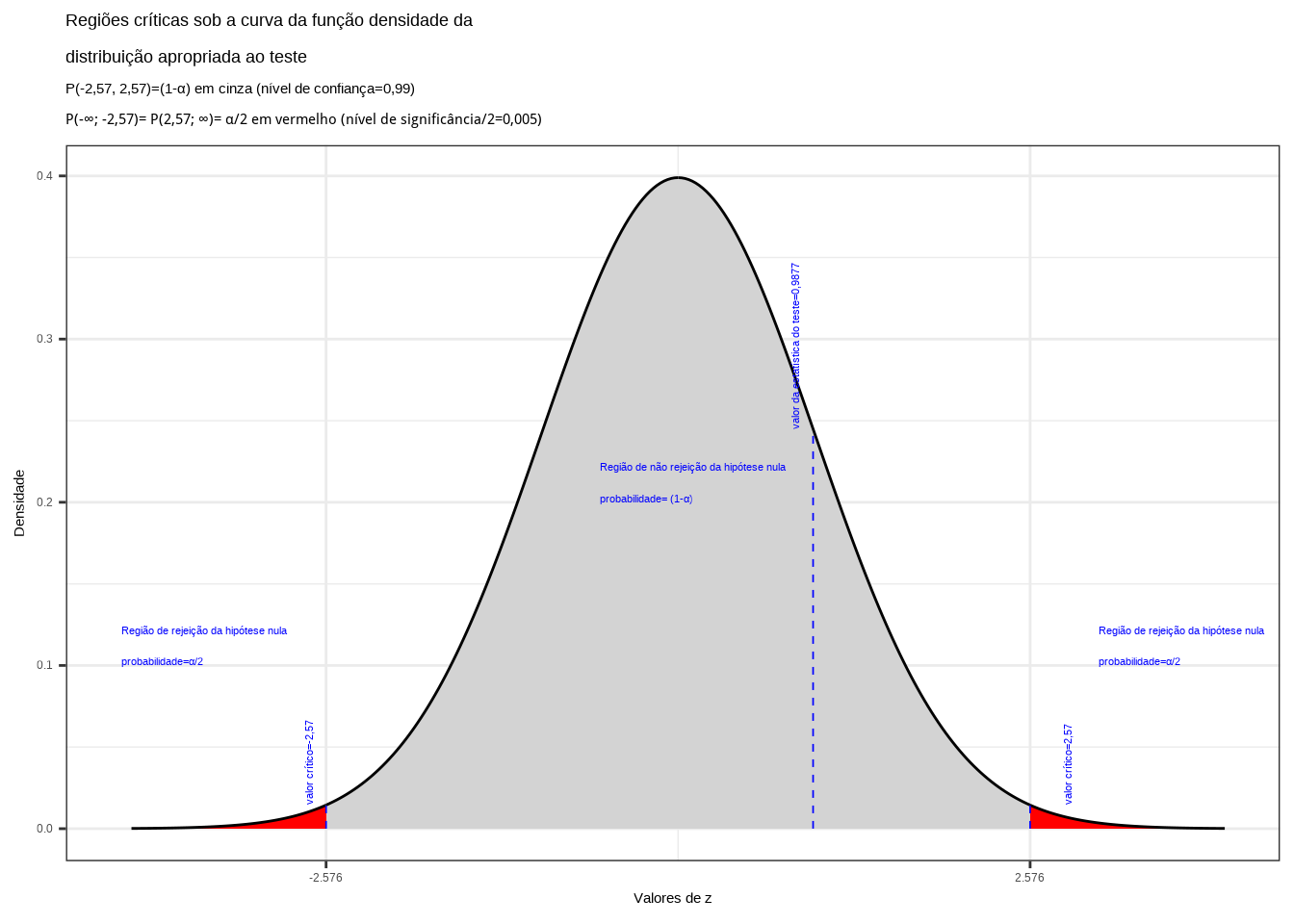

Figure 11.18: Regiões de rejeição da hipótese nula para o teste bilateral (tipo: diferente de) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valores críticos da estatística do teste: \(z_{crit} =\pm 2,57\). O valor calculado da estatística (\(z_{calc}=0,987\)) não nos possibilita a rejeição da hipótese nula sob aquele nível de confiança

Conclusão: Os resultados obtidos pela análise estatística de comparação de médias das duas amostras colhidas de garrafas de plástico enchidas por duas máquinas diferentes \(1\) e \(2\) não nos permitem rejeitar a hipótese de que suas médias sejam iguais sob um nível de confiança de 99% (Figura 11.18).

Podemos ainda realizar testes de hipóteses para as diferenças entre as médias observadas (\(\mu_{1}<\mu_{2}\) ou \(\mu_{1}>\mu_{2}\)). As conclusões derivadas desses testes deverão indicar que as médias não diferem entre si ao nível de significância dos testes chegando assim, por outras vias (agora não se rejeitando a hipótese nula), à mesma conclusão do teste de igualdade das médias antes realizado.

Teste unilateral à esquerda (tipo: menor que)

Nessa situação postula-se que a diferença da média 1 para a média 2 é no mínimo 0 (o que equivale dizer que a média 1 é no mínimo igual à média 2):

\[ \begin{cases} H_{0}: \mu_{1} - \mu_{2} \ge 0 \\ H_{1}: \mu_{1} - \mu_{2} < 0 \end{cases} \]

Da tabela da distribuição Normal padronizada obtemos o valor crítico monocaudal: \({Z}_{tab\left(\alpha \right)}=-2,33\). Pelo cálculo, a estatística do teste é \(Z_{calc}=0,98773\).

alfa=0.01
prob_desejada=alfa
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)

z_calculado=0.98773
d_calculado=dnorm(z_calculado, 0, 1)




ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-4, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de z", breaks = c(z_desejado))  +
  labs(title= 
         "Região crítica sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P( -2,33,\U221e,)=(1-\u03b1) em cinza (nível de confiança=0,99) \nP(-\U221e; -2,33)=\u03b1 em vermelho (nível de significância=0,01) ")+
geom_segment(aes(x = z_desejado, y = 0, xend = z_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
annotate(geom="text", x=z_desejado-0.1, y=d_desejada, label="valor crítico=-2,33", angle=90, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado-2, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1", angle=0, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado+1, y=0.2, label="Região de não rejeição da hipótese nula  \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  geom_segment(aes(x = z_calculado, y = 0, xend = z_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_calculado-0.1, y=d_calculado, label="valor da estatística do teste=0,98773", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()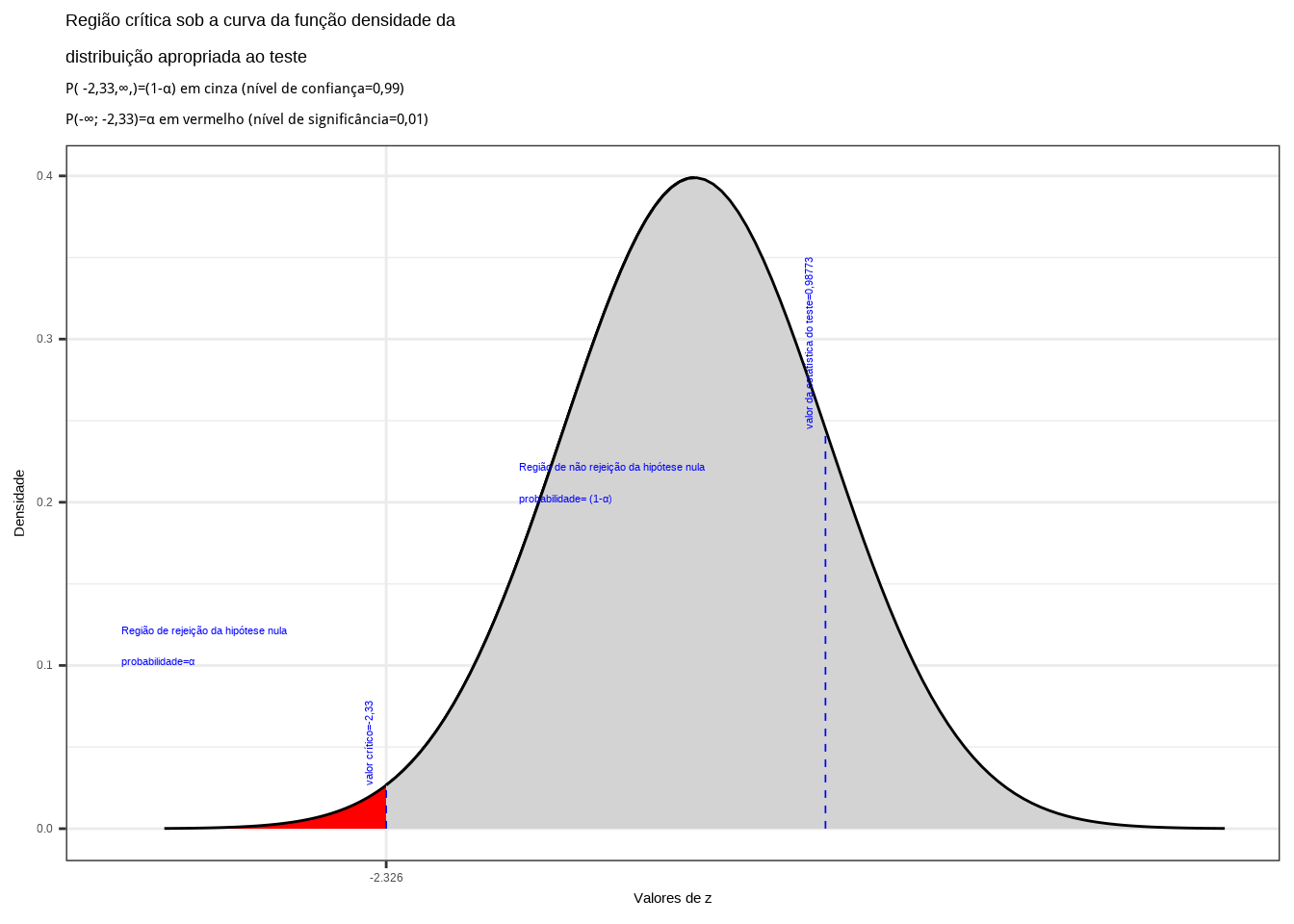

Figure 11.19: Regiões de rejeição da hipótese nula para o teste unilateral à esquerda (tipo: menor que) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valor crítico da estatística do teste: \(z_{crit}=-2,33\). O valor calculado da estatística (\(z_{calc}=0,98773\)) não nos possibilita a rejeição da hipótese nula sob aquele nível de confiança

Conclusão: Os resultados obtidos pela análise estatística de comparação de médias das duas amostras colhidas de garrafas de plástico enchidas por duas máquinas diferentes \(1\) e \(2\) não nos permitem rejeitar a hipótese de que a média de enchimento da máquina 1 seja no mínimo igual à da máquina 2 sob um nível de confiança de 99% (Figura 11.19).

Teste unilateral à direita (tipo: maior que)

Nessa situação postula-se que a diferença da média 1 para a média 2 é no máximo 0 (o que equivale dizer que a média 1 é no máximo igual à média 2):

\[ \begin{cases} H_{0}: \mu_{1} - \mu_{2} \le 0 \\ H_{1}: \mu_{1} - \mu_{2} > 0 \\ \end{cases} \]

Da tabela da distribuição Normal padronizada obtemos o valor crítico monocaudal: \({Z}_{tab\left(\alpha \right)}=-2,33\). Pelo cálculo, a estatística do teste é \(Z_{calc}=0,98773\).

alfa=0.99
prob_desejada=alfa
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)

z_calculado=0.98773
d_calculado=dnorm(z_calculado, 0, 1)




ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(-4, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de z", breaks = c(z_desejado))  +
  labs(title= 
         "Região crítica sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P(- \U221e; 2,33)=(1-\u03b1) em cinza (nível de confiança=0,99) \nP(2,33 ; \U221e)=\u03b1 em vermelho (nível de significância=0,01) ")+
geom_segment(aes(x = z_desejado, y = 0, xend = z_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
annotate(geom="text", x=z_desejado-0.1, y=d_desejada, label="valor crítico=-1,88", angle=90, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1", angle=0, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado-3, y=0.2, label="Região de não rejeição da hipótese nula  \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  geom_segment(aes(x = z_calculado, y = 0, xend = z_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_calculado-0.1, y=d_calculado, label="valor da estatística do teste=0,98773", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()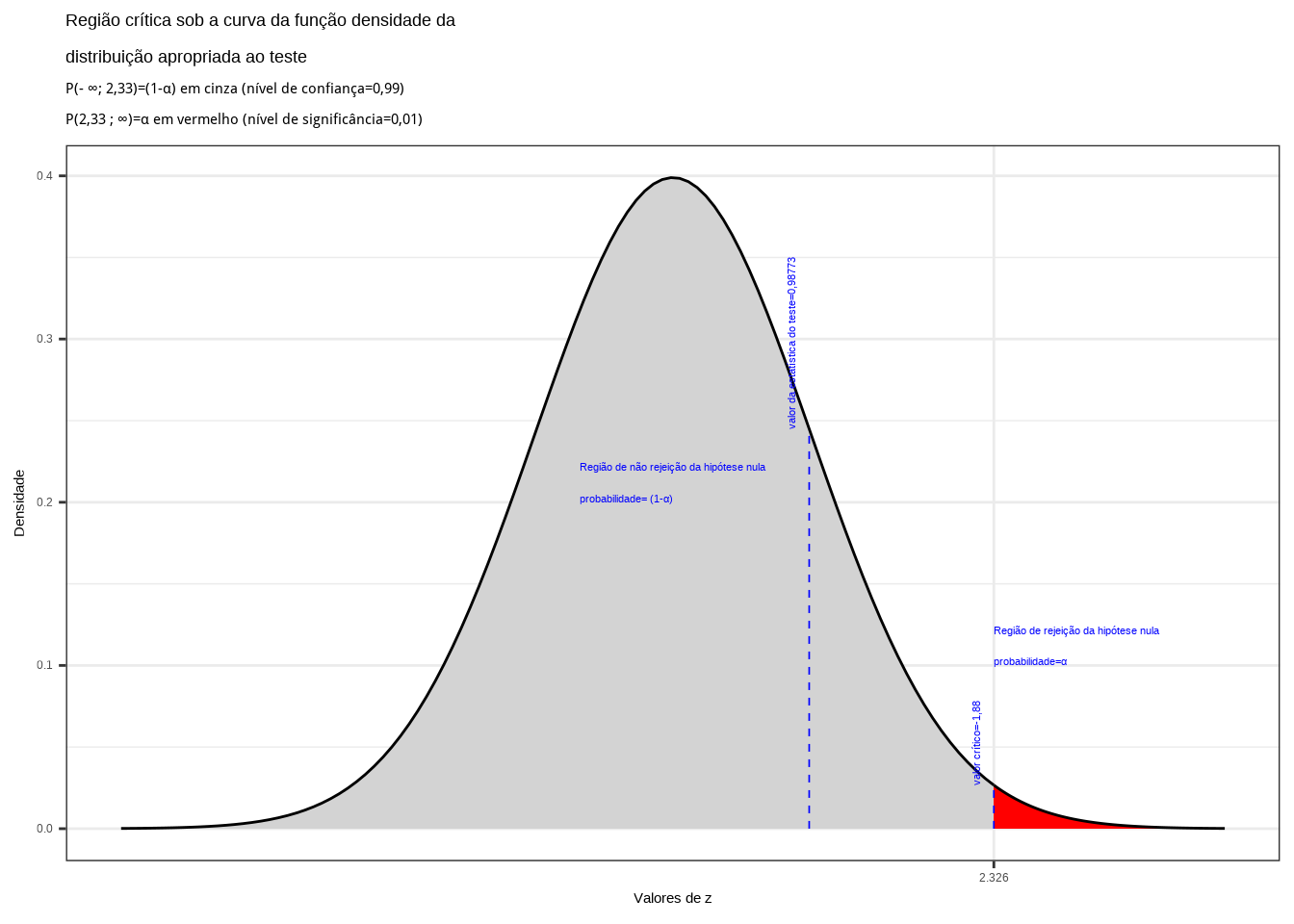

Figure 11.20: Região de rejeição da hipótese nula para o teste unilateral à direita (tipo: maior que) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: \(z_{crit} = 2,33\). O valor calculado da estatística (\(z_{calc}=0,98773\)) não nos possibilita a rejeição da hipótese nula sob aquele nível de confiança

Conclusão: Os resultados obtidos pela análise estatística de comparação de médias das duas amostras colhidas de garrafas de plástico enchidas por duas máquinas diferentes \(1\) e \(2\) não nos permitem rejeitar a hipótese de que a média de enchimento da máquina 1 seja no máximo igual à da máquina 2 sob um nível de confiança de 99% (Figura 11.20).

Pelo teste unilateral à esquerda concluiu-se que \(\mu_{1} \ge \mu_{2}\); pelo teste unilateral à direita conclui-se que \(\mu_{1} \le \mu_{2}\). Sob o nível de significânca estabelecido conclui-se que \(\mu_{1} = \mu_{2}\).

11.9.3 Testes de hipóteses para as médias de duas populações Normais com variâncias desconhecidas mas iguais: teste “t’’ homocedástico (\(\sigma_{1}^{2}=\sigma_{2}^{2}=?\))

Probabilidade dos intervalos de confiança para os testes de hipóteses com o uso da estatística t (\(T \sim t_{(n_{1} + n_{2} - 2)}\)). Os valores assumidos pelas diferenças amostrais são tais que

\[ T = \frac{(\stackrel{-}{x}_{1} - \stackrel{-}{x}_{2})-\Delta_{0}} {S_{c} \cdot \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}} \sim t_{(n_{1} + n_{2} - 2)} \]

em que:

• \(\Delta_{0}\) usualmente é 0 (igualdade);
  
• \(\sigma_{1}^{2} = \sigma_{2}^{2} = \sigma^{2}\) são as variâncias populacionais desconhecidas, mas admitidas iguais (homogêneas);
  
• \(\stackrel{-}{x}_{1}, S_{1}^{2}, n_{1}\) são a média, a variância e o tamanho referentes à amostra 1;
  
• \(\stackrel{-}{x}_{2}, S_{2}^{2}, n_{2}\) são a média, a variância e o tamanho referentes à amostra 2; e,
  
• \(S_{c}^{2}\) é a variância conjunta ou ponderada.

Condições:

• amostras Normais (\(n_{1}\) e \(n_{2}\) qualquer);
  
• amostras sob outras distribuições (desde que \(n_{1}\) e \(n_{2}\) \(\ge 30\));
  
• a utilização da estatística ``t’’ para \(n_{1}\) e \(n_{2} \ge 30\) apenas pressupõe que \(S_{c}\) e seja um estimador suficientemente bom para \(\sigma_{i}\); e,
• \({t}_{tab\left(\frac{\alpha }{2};{n}_{1}+{n}_{2}-2\right)}\) ou \({t}_{tab\left(\alpha ;{n}_{1}+{n}_{2}-2\right)}\): o quantil associado na distribuição ``t’’ de Student ao nível de significância pretendido no teste, com \(({n}_{1}+{n}_{2}-2)\) graus de liberdade.

A variância conjunta (ou variância ponderada) \(S_{c}^{2}\) a ser utilizada no cálculo da estatística do teste é definida como:

\[ S_{c}^{2} = \frac{\left({n}_{1}-1\right)\cdot {S}_{1}^{2}+\left({n}_{2}-1\right)\cdot {S}_{2}^{2}}{{n}_{1}+{n}_{2}-2} \]

Probabilidade dos intervalos de confiança para os testes de hipóteses com o uso da estatística t (T \(\sim t_{(n_{1} + n_{2} - 2)}\))

• Teste de hipóteses bilateral (tipo: diferente de):

\[\begin{align*} P[\left|t_{calc}\right| \ge {t}_{tab\left(\frac{\alpha }{2};{n}_{1}+{n}_{2}-2\right)}|\mu_{1}=\mu_{2}] & =(1-\alpha) \\ P(- {t}_{tab\left(\frac{\alpha }{2};{n}_{1}+{n}_{2}-2\right)} \le t_{calc} \le {t}_{tab\left(\frac{\alpha }{2};{n}_{1}+{n}_{2}-2\right)}) & =(1-\alpha)\\ \end{align*}\]

• Teste de hipóteses unilateral à esquerda (tipo: menor que):

\[\begin{align*} P[t_{calc} \ge -{t}_{tab\left(\alpha \right)}|\mu_{1} \ge \mu_{2}] & = (1-\alpha) \\ P( t_{calc} \ge -{t}_{tab\left(\alpha;{n}_{1}+{n}_{2}-2\right)} ) & = (1-\alpha) \\ \end{align*}\]

• Teste de hipóteses unilateral à direita (tipo: maior que):

\[\begin{align*} P[t_{calc} \le {t}_{tab\left(\alpha \right)}|\mu_{1} \le \mu_{2}] & =(1-\alpha) P( t_{calc} \le {t}_{tab\left(\alpha;{n}_{1}+{n}_{2}-2\right)}) & = (1-\alpha) \end{align*}\]

Nas figuras 11.8, 11.9 e 11.10 observam-se:

 

• as regiões de rejeição da hipótese nula (subdivididas nos dois ou em apenas um dos lados) sob a curva da função densidade de probabilidade da distribuição adequada ao teste com probabilidades iguais ao nível de significância \(\alpha\) ;
  
• a região de não rejeição da hipótese nula (delimitada à esquerda e à direita ou apenas em um dos lados) com probabilidade igual ao nível de confiança \((1-\alpha)\); e,
  
• os valores críticos da estatística do teste.

11.9.3.1 Teste “F” para a razão de duas variâncias

Para se verificar se a consideração de igualdade das variâncias é estatisticamente sustentável pode-se recorrer ao teste ``F’’ de sua razão. Estrutura do teste:

\[ \begin{cases} H_{0}: \sigma_{1}^{2}-\sigma_{2}^{2}=\delta \\ H_{1}: \sigma_{1}^{2} - \sigma_{2}^{2} \ne \delta \end{cases} \]

em que, usualmente, \(\delta=0\) (igualdade).

Tendo-se \(\frac{({\sigma }_{2}^{2}}{{\sigma }_{1}^2}=\frac{{\sigma }_{1}^{2}}{{\sigma }_{2}^2}=1)\) na Hipótese nula (\(H_{0}\)) pela pressuposição da igualdade, \(F_{calc}\) será dado por:

\[ f_{calc} = (\frac{{S}_{1}^{2}}{{S}_{2}^{2}})\cdot (\frac{{\sigma }_{1}^{2}}{{\sigma }_{2}^2}) \sim F_{(n_{1} -1), (n_{2} -1)} \]

A Hipótese nula será rejeitada se:

\[ f_{calc} \ge f_{((n_{1} -1), (n_{2} -1), 1-\frac{\alpha}{2})} \]

ou

\[ f_{calc} \le f_{((n_{1} -1), (n_{2} -1), \frac{\alpha}{2})} \]

em que \({f}_{({n}_{1}-1),({n}_{2}-1)}\) são os quantis de ordem \(\alpha\) (pelo lado esquerdo da curva) e \((1-\frac{\alpha}{2})\) (pelo lado direito da curva) da Distribuição F (Ronald Fisher e George Waddel Snedecor) com graus de liberdade: \((n_{1}-1)\) são os graus de liberdade (GL) no numerador e \((n_{2}-1)\) são os graus de liberdade (GL) no denominador (em concordância com a razão utilizada (\(\frac{S_{1}}{S_{2}}\)).

Em razão da limitação das tabelas torna-se interessante relembrar a propriedade:

\[ {f}_{(({n}_{1}-1),({n}_{2}-1), \alpha)} = \frac{1}{ {f}_{(({n}_{1}-1),({n}_{2}-1), (1-\frac{\alpha}{2}))} } \]

Regiões de rejeição da hipótese nula (Figura 11.21):

prob_desejada1=0.025
prob_desejada2=0.975

df1=3
df2=50  

f_desejado1=round(qf(prob_desejada1,df1, df2), 4)
f_desejado2=round(qf(prob_desejada2,df1, df2), 4)

d_desejada1=df(f_desejado1,df1, df2)
d_desejada2=df(f_desejado2,df1, df2)


f_test_1=ggplot(data.frame(x = c(0, 6)), aes(x)) +
  stat_function(fun = df,
                geom = "area",
                fill = "red",
                xlim = c(0,f_desejado1),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  stat_function(fun = df,
                geom = "area",
                fill = "lightgrey",
                xlim = c(f_desejado1, f_desejado2),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  stat_function(fun = df,
                geom = "area",
                fill = "red",
                xlim = c(f_desejado2,6),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  scale_y_continuous(name="Densidade") +
  #scale_x_continuous(name="Valores score (f)", breaks = c(f_desejado1, f_desejado2))+  
  scale_x_continuous(name="Valores score (f)")+  
  labs(title="Curva da função densidade \nDistribuição F", 
  subtitle = "P(f crítico 1, f crítico 2)=(1-\u03b1) em cinza (nível de confiança) \nP(0; f crítico 1)= P(f crítico 2; \U221e)= \u03b1/2 em vermelho (nível de significância/2) ")+
  geom_segment(aes(x = f_desejado1, y = 0, xend = f_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = f_desejado2, y = 0, xend = f_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=f_desejado1+0.2, y=0.2, label="f crítico 1", angle=90, vjust=0, hjust=0, color="blue",size=4)+
  annotate(geom="text", x=f_desejado2-0.2, y=0.2, label="f crítico 2", angle=90, vjust=0, hjust=0, color="blue",size=4)+
  annotate(geom="text", x=f_desejado1+1, y=0.4, label="Zona de não rejeição \n(para f calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=f_desejado2+1, y=0.2, label="Zona de rejeição  \n(para f calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=f_desejado1-1, y=0.2, label="Zona de rejeição  \n(para f calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()

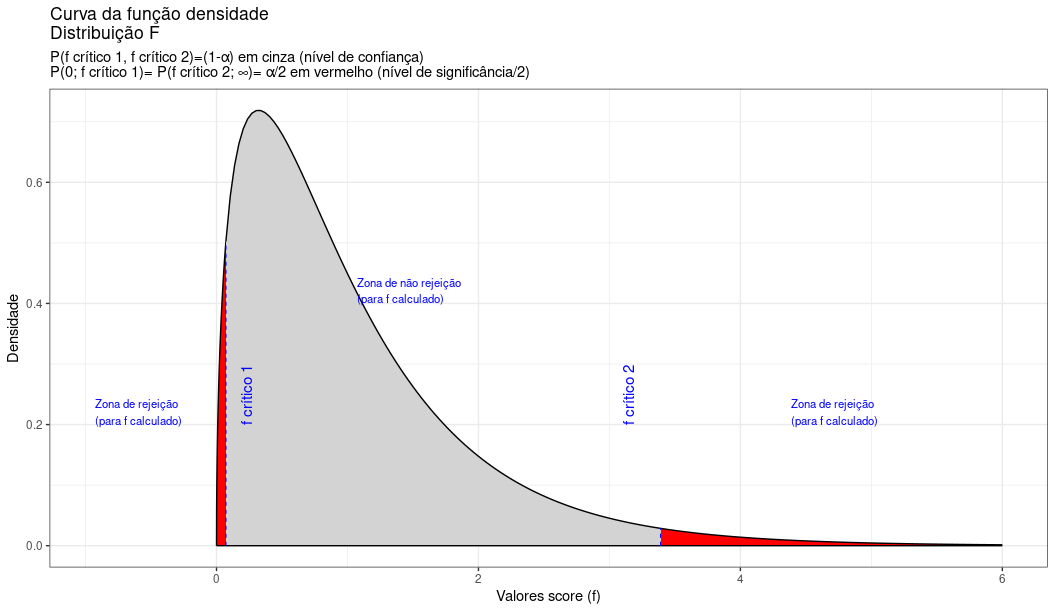
Figure 11.21: Regiões de rejeição da hipótese nula para o teste bilateral (tipo: diferente de) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valores críticos da estatística do teste: \(f_{crit1}\) e \(f_{crit2}\) para o nível de significância pretendido (\(\alpha\) dividido em ambas as caudas) e (\(df_{1}; df_{2}\)) graus de liberdade. A curva não é simétrica e assim, os valores críticos são diferentes

Uma regra prática permite reverter o teste bilateral em um teste unilateral à direita se tomarmos o maior valor (\(f_{calc}\) maior que 1, portanto) de \(f_{calc}\) dentre as possíveis razões:

\[ f_{calc} = (\frac{{S}_{1}^{2}}{{S}_{2}^{2}})\cdot (\frac{{\sigma }_{1}^{2}}{{\sigma }_{2}^2}) \sim F(_{(n_{1} -1), (n_{2} -1))} \]

ou

\[ f_{calc} = (\frac{{S}_{2}^{2}}{{S}_{1}^{2}})\cdot (\frac{{\sigma }_{2}^{2}}{{\sigma }_{1}^2}) \sim F(_{(n_{2} -1), (n_{1} -1))} \]

em que:

• \({F}_{tab\left(\alpha ,{n}_{1}-1,{n}_{2}-1\right)}\) é o quantil de ordem \(\alpha\) da Distribuição ``F’’ (Ronald Fisher e George Waddel Snedecor) com graus de liberdade \((n_{1}-1)\) no numerador e \((n_{2}-1)\) no denominador (em concordância com a razão utilizada: \(\frac{S_{1}}{S_{2}}\)); ou,
• \((n_{2}-1)\) são os graus de liberdade (GL) no numerador e \((n_{1}-1)\) são os graus de liberdade (GL) no denominador (em concordância com a razão utilizada: \(\frac{S_{2}}{S_{1}}\)).

Região de rejeição da hipótese nula (Figura 11.22):

prob_desejada1=0.95

df1=3
df2=50  

f_desejado1=round(qf(prob_desejada1,df1, df2), 4)
d_desejada1=df(f_desejado1,df1, df2)



df_test_2=ggplot(data.frame(x = c(0, 6)), aes(x)) +
  stat_function(fun = df,
                geom = "area",
                fill = "lightgrey",
                xlim = c(0,f_desejado1),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  stat_function(fun = df,
                geom = "area",
                fill = "red",
                xlim = c(f_desejado1,6),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  scale_y_continuous(name="Densidade") +
  #scale_x_continuous(name="Valores score (f)", breaks = c(f_desejado1, f_desejado2))+  
  scale_x_continuous(name="Valores score (f)")+  
  labs(title="Curva da função densidade \nDistribuição F", 
  subtitle = "P(0; f crítico 1)=(1-\u03b1) em cinza (nível de confiança) \nP(f crítico ; \U221e)= \u03b1 em vermelho (nível de significância) ")+
  geom_segment(aes(x = f_desejado1, y = 0, xend = f_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=f_desejado1+0.1, y=d_desejada1, label="f crítico 1", angle=90, vjust=0, hjust=0, color="blue",size=4)+
 annotate(geom="text", x=f_desejado1+1, y=d_desejada1, label="Zona de rejeição \n(para f calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=f_desejado1-1, y=d_desejada1, label="Zona de não rejeição  \n(para f calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()

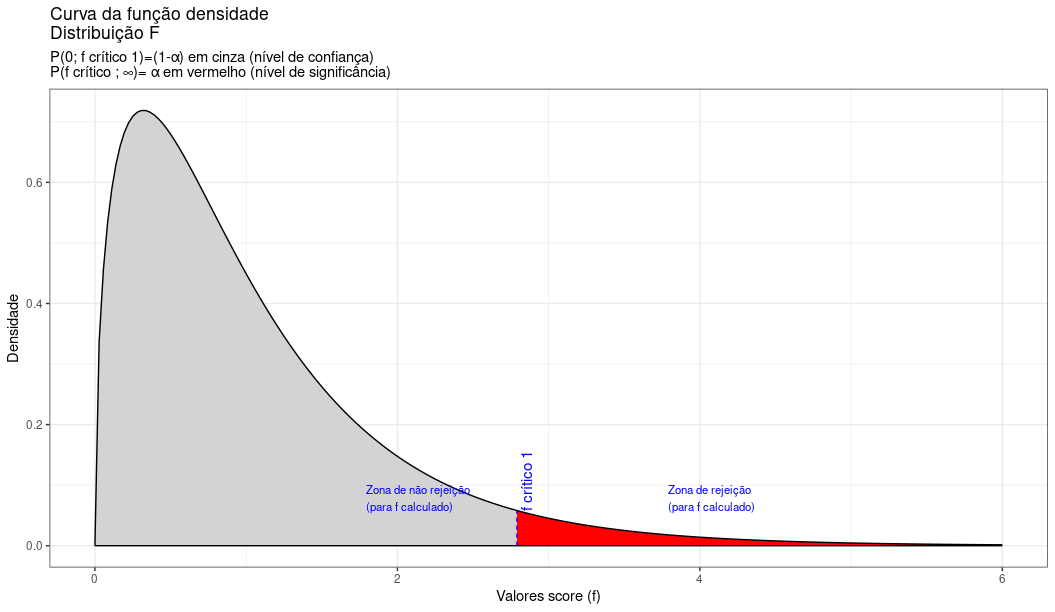
Figure 11.22: Região de rejeição da hipótese nula para o teste uniletaral à direita (tipo: menor que): a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: \(f_{crit}\) para o nível de significância pretendido (\(\alpha\) em uma cauda) e (\(df_{1}; df_{2}\)) graus de liberdade.

Exemplo: A Secretaria de Educação de um município deseja saber se o desempenho dos alunos de duas diferentes escolas municipais na disciplina de matemática pode ser considerado igual a um nível de significância de \(\alpha=0,05\). Verifique antes de as variâncias são . Para tanto ministrou um mesmo teste a 10 alunos de cada uma delas e obteve os seguintes notas:

Notas em matemática de duas escolas

Escola 01		Escola 02
78	83	85	79
84	79	75	88
81	75	83	94
78	85	87	87
76	81	80	82

• Teste de hipóteses para a igualdade das variâncias:

\[ \begin{cases} H_{0}: \sigma_{1}^{2}-\sigma_{2}^{2}=\delta \\ H_{1}: \sigma_{1}^{2} - \sigma_{2}^{2} \ne \delta \end{cases} \]

em que, usualmente, \(\delta=0\) (igualdade). Se \(\sigma_{1}^{2}=\sigma_{2}^{2}\), então \(\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}=1\).

\[ F_{cal}=\frac{{S}_{2}^{2}}{{S}_{1}^{2}}\cdot \frac{{\sigma }_{2}^{2}}{{\sigma }_{1}^2}=2,56 \]

\[ F_{critico\left(\alpha ,{n}_{1}-1,{n}_{2}-1\right)} = F_{tab\left(5\% ,9,9\right)} = 3,18 \]

prob_desejada1=0.95

df1=9
df2=9  

f_desejado1=round(qf(prob_desejada1,df1, df2), 4)
d_desejada1=df(f_desejado1,df1, df2)

f_calculado=2.56
d_calculado=df(f_calculado,df1, df2)

f_test_3=ggplot(data.frame(x = c(0, 6)), aes(x)) +
  stat_function(fun = df,
                geom = "area",
                fill = "lightgrey",
                xlim = c(0,f_desejado1),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  stat_function(fun = df,
                geom = "area",
                fill = "red",
                xlim = c(f_desejado1,6),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  scale_y_continuous(name="Densidade") +
  #scale_x_continuous(name="Valores score (f)", breaks = c(f_desejado1, f_desejado2))+  
  scale_x_continuous(name="Valores score (f)")+  
  labs(title="Curva da função densidade \nDistribuição F", 
  subtitle = "P(0; 3,18 1)=(1-\u03b1) em cinza (nível de confiança=0,95) \nP(3,18 ; \U221e)= \u03b1 em vermelho (nível de significância=0,05) ")+
  geom_segment(aes(x = f_desejado1, y = 0, xend = f_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=f_desejado1+0.1, y=d_desejada1, label="F crítico 1=3,18", angle=90, vjust=0, hjust=0, color="blue",size=4)+
 annotate(geom="text", x=f_desejado1+1, y=d_desejada1, label="Zona de rejeição \n(para F calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=f_desejado1-2, y=d_desejada1, label="Zona de não rejeição  \n(para F calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
    geom_segment(aes(x = f_calculado, y = 0, xend = f_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=f_calculado+0.1, y=d_calculado, label="f calculado=2,56", angle=90, vjust=0, hjust=0, color="blue",size=4)+
  theme_bw()

O valor calculado da estatística de teste (\(F_{calc}=2,56\)) situa-se na região não significante do teste, não permitindo a rejeição da hipótese nula de que as variâncias sejam iguais sob o nível de confiança estabelecido. Não se pode rejeitar a hipótese de que as variâncias sejam iguais a um nível de significância de 5% (Figura 11.23).

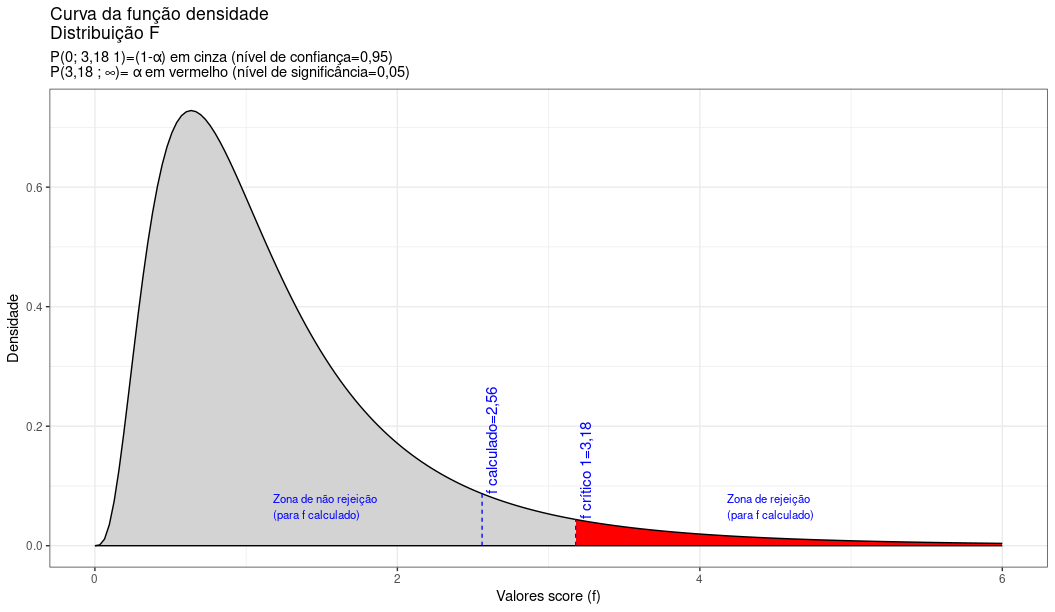
Figure 11.23: O valor calculado da estatística de teste (\(F_{calc}=2,56\)) situa-se na região não significante do teste, não permitindo a rejeição da hipótese nula de que as variâncias são iguais sob o nível de confiança estabelecido.

Estrutura do teste:

\[ \begin{cases} H_{0}: \mu_{1} - \mu_{2} = 0 \\ H_{1}: \mu_{1} - \mu_{2} \ne 0 \\ \end{cases} \]

Variâncias populacionais desconhecidas mas estatisticamente iguais. Nada se sabe sobre a distribuição da população e amostras de reduzido tamanho.

\[ S_{c}^{2} = \frac{\left({n}_{1}-1\right)\cdot {S}_{1}^{2}+\left({n}_{2}-1\right)\cdot {S}_{2}^{2}}{{n}_{1}+{n}_{2}-2} \]

é a variância conjunta ponderada, em que:

• \(\mu_{1} , \mu_{2}\) são as médias das populações em teste;
  
• \(\sigma_{1}^{2}=\sigma_{2}^{2}=\sigma^{2}\) são as variâncias das populações em teste, desconhecidas e estatisticamente iguais;
  
• \(\stackrel{-}{x}_{1}=80, S_{1}^{2}= 3,366^{2} , n_{1}=10\) são a média, a variância e o tamanho referentes à amostra 1;
  
• \(\stackrel{-}{x}_{2}=84, S_{2}^{2}= 5,395^{2} , n_{2}=10\) são a média, a variância e o tamanho referentes à amostra 2;
  
• \({t}_{tab\left(\frac{\alpha }{2};{n}_{1}+{n}_{2}-2\right)}\): o quantil associado na distribuição ``t’’ de Student ao nível de significância pretendido no teste, com \(({n}_{1}+{n}_{2}-2)\) graus de liberdade.

\[\begin{align*} S_{c}^{2} & = 20,2180\\ S_{c} & = 4,4964 \end{align*}\]

Estatística do teste:

\[ t_{calc} = \frac{(\stackrel{-}{x}_{1} - \stackrel{-}{x}_{2})} {S_{c} \cdot \sqrt{\frac{1}{n_{1}}+\frac{1}{n_{2}}}} \]

\[ t_{cal}= -1,9892 \]

Teste bilateral:

\[ {t}_{tab\left(\frac{\alpha }{2};{n}_{1}+{n}_{2}-2\right)} < t_{calc} < {t}_{tab\left(\frac{\alpha }{2};{n}_{1}+{n}_{2}-2\right)} \]

\[ |{t}_{tab\left(\frac{\alpha }{2};{n}_{1}+{n}_{2}-2\right)}|=|{t}_{tab\left(2.5\%;18\right)}|=2,101 \]

alfa=0.05

prob_desejada1=alfa/2
df=8
t_desejado1=round(qt(prob_desejada1,df ),df)
d_desejada1=dt(t_desejado1,df)

prob_desejada2=1-alfa/2
df=8
t_desejado2=round(qt(prob_desejada2, df),df)
d_desejada2=dt(t_desejado2,df)

t_calculado=-1.9892
d_calculado=dt(t_calculado,df)


ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dt,
            args=list(df), 
            fill = "red", 
            xlim = c(-4, t_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(t_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(0, t_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "red", 
            xlim = c(t_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de t", breaks = c(t_desejado1, t_desejado2))  +
  labs(title= 
         "Regiões críticas sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P(-2,101, 2,101)=(1-\u03b1) em cinza (nível de confiança=0,95) \nP(-\U221e; -2,101)= P(2,101; \U221e)= \u03b1/2 em vermelho (nível de significância/2=0,025) ")+ geom_segment(aes(x = t_desejado1, y = 0, xend = t_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
 geom_segment(aes(x = t_desejado2, y = 0, xend = t_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=t_desejado1-0.1, y=d_desejada1, label="valor crítico=-2,101", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado2+0.3, y=d_desejada2, label="valor crítico=2,101", angle=90, vjust=0, hjust=0, color="blue",size=3)+
 annotate(geom="text", x=t_desejado1-2, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
 annotate(geom="text", x=t_desejado2+0.5, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
 annotate(geom="text", x=t_desejado1+2, y=0.2, label="Região de não rejeição da hipótese nula \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
 geom_segment(aes(x = t_calculado, y = 0, xend = t_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
 annotate(geom="text", x=t_calculado-0.1, y=d_calculado, label="valor da estatística do teste=-1,9892", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()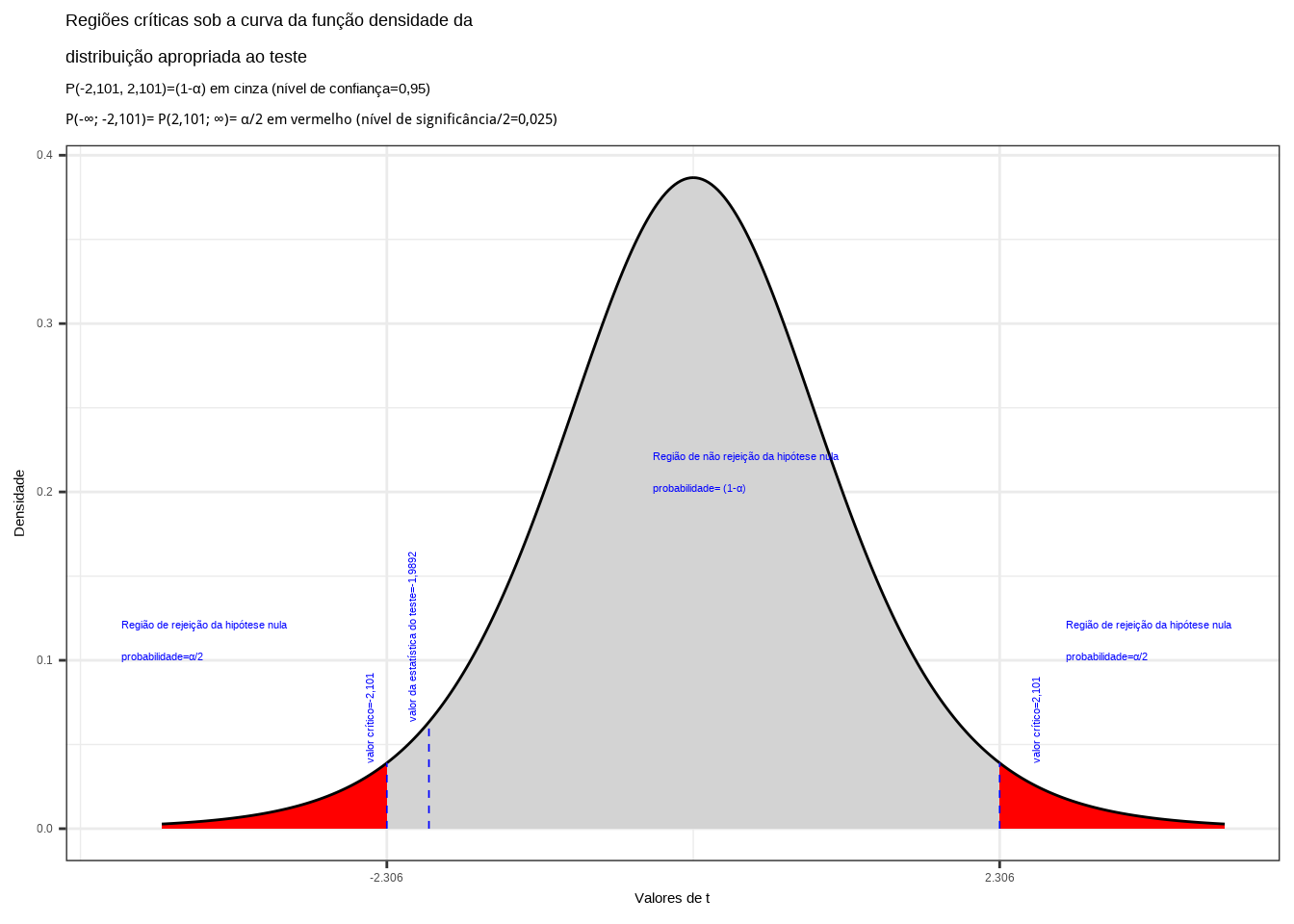

Figure 11.24: Regiões de rejeição da hipótese nula para o teste bilateral (tipo: diferente de) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valores críticos da estatística do teste: \(t_{crit} =\pm 2,101\). O valor calculado da estatística (\(t_{calc}=-1,9892\)) situa-se na faixa de não significância do teste, impossibilitando a rejeição da hipótese nula sob aquele nível de confiança

Conclusão: Os resultados obtidos pela análise estatística de comparação de médias das duas amostras colhidas das notas de testes de matemáticas realizados em duas escolas diferentes (escola 1 e escola 2) não nos permitem rejeitar a hipótese de que suas médias sejam iguais a um nível de confiança de 5% (Figura 11.24).

11.9.4 Teste de hipóteses para as médias de duas populações Normais com variâncias desconhecidas e desiguais: teste “``t’’ heterocedástico (\(\sigma_{1}^{2} \neq \sigma_{2}^{2}=?\))

Probabilidade dos intervalos de confiança para os testes de hipóteses com o uso da estatística t (\(T \sim t_{\nu}\)). Os valores assumidos pelas diferenças amostrais são tais que

\[ T = \frac{(\stackrel{-}{x}_{1} - \stackrel{-}{x}_{2})-\Delta_{0}}{ \sqrt{\frac{S_{1}^{2}}{n_{1}}+\frac{S_{2}^{2}}{n_{2}}}} \sim t_{\nu} \]

em que:

• \(\Delta_{0}\) usualmente é 0 (igualdade);
  
• \(\stackrel{-}{x}_{1}, S_{1}^{2}, n_{1}\) são a média, a variância e o tamanho referentes à amostra 1;
  
• \(\stackrel{-}{x}_{2}, S_{2}^{2}, n_{2}\) são a média, a variância e o tamanho referentes à amostra 2; e,
  
• a aproximação dos graus de liberdade (\(\nu\)) é dada por uma combinação linear de variâncias de amostras independentes (Welch-Satterhwaite, 1946)

\[ \nu=\frac{{\left(\frac{{S}_{1}^{2}}{{n}_{1}}+\frac{{S}_{2}^{2}}{{n}_{2}}\right)}^{2}}{\frac{{\left(\frac{{S}_{1}^{2}}{{n}_{1}}\right)}^{2}}{{n}_{1}-1}+\frac{{\left(\frac{{S}_{2}^{2}}{{n}_{2}}\right)}^{2}}{{n}_{2}-1}} \]

Condições:

• amostras Normais (\(n_{1}\) e \(n_{2}\) qualquer);
  
• amostras sob outras distribuições (desde que \(n_{1}\) e \(n_{2}\) \(\ge 30\));
  
• \({t}_{tab\left(\frac{\alpha }{2};\nu\right)}\) ou \({t}_{tab\left(\alpha ;\nu\right)}\): o quantil associado na distribuição ``t’’ de Student ao nível de significância pretendido no teste, com \(\nu\) graus de liberdade.

Probabilidade dos intervalos de confiança para os testes de hipóteses com o uso da estatística t (T \(\sim t_{\nu}\))

• Teste de hipóteses bilateral (tipo: diferente de):

\[\begin{align*} P[\left|t_{calc}\right| \ge {t}_{tab\left(\frac{\alpha }{2};\nu \right)} |\mu_{1} = \mu_{2} ] & = (1-\alpha) \\ P( - {t}_{tab\left(\frac{\alpha }{2};\nu \right)} \le t_{calc} \le {t}_{tab\left(\frac{\alpha }{2};\nu \right)} ) & = (1-\alpha) \\ \end{align*}\]

• Teste de hipóteses unilateral à esquerda (tipo: menor que):

\[\begin{align*} P[t_{calc} \ge {t}_{tab \left(\alpha ;\nu \right)} |\mu_{1} \ge \mu_{2}] & = (1-\alpha) \\ P(t_{calc} \ge {t}_{tab \left(\alpha ;\nu \right)}) & = (1-\alpha) \\ \end{align*}\]

• Teste de hipóteses unilateral à direita (tipo: maior que):

\[\begin{align*} P[t_{calc} \le {t}_{tab \left(\alpha ;\nu \right)}|\mu_{1} \le \mu_{2}] & = (1-\alpha) \\ P( t_{calc} \le {t}_{tab \left(\alpha ;\nu \right)} ) & = (1-\alpha) \\ \end{align*}\]

Exemplo: a Secretaria de Educação de um município deseja saber se o desempenho dos alunos de duas diferentes escolas municipais na disciplina de matemática pode ser considerado igual a um nível de significância de \(\alpha=0,05\) (verifique antes se as variâncias podem ser admitidas como iguais). Para tanto ministrou um mesmo teste a 10 alunos de cada uma delas e obteve os seguintes notas:

Desempenho dos alunos de duas escolas

Escola 01		Escola 02
68	94	85	79
51	100	75	88
50	75	83	94
81	70	87	87
100	20	80	82

Estrutura do teste:

\[ \begin{cases} H_{0}: \mu_{1} - \mu_{2} = 0 \\ H_{1}: \mu_{1} - \mu_{2} \ne 0 \end{cases} \]

• Teste de hipóteses bilateral (tipo: diferente de):

\[ P (- {t}_{tab\left(\frac{\alpha }{2};\nu \right)} \le t_{calc} \le {t}_{tab\left(\frac{\alpha }{2};\nu \right)}) = (1-\alpha) \]

As variâncias populacionais não são conhecidas e o tamanho das amostras é reduzido.

Teste de hipóteses para a igualdade das variâncias:

\[ \begin{cases} H_{0}: \sigma_{1}^{2}-\sigma_{2}^{2}=\delta & \text{usualmente $\delta=0$ (igualdade)}\\ H_{1}: \sigma_{1}^{2} - \sigma_{2}^{2} \ne \delta \end{cases} \]

Se \(\sigma_{1}^{2}=\sigma_{2}^{2}\), então \(\frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}=1\). O maior valor de \(F_{calc}\) é dado por:

\[ F_{cal}=\frac{{S}_{1}^{2}}{{S}_{2}^{2}}\cdot \frac{{\sigma }_{1}^{2}}{{\sigma }_{2}^2}=22,056 \]

e o valor crítico é

\[ {F}_{tab\left(\alpha ,{n}_{1}-1,{n}_{2}-1\right)} = {F}_{tab\left(5\% ,9,9\right)} = 3,18 \]

prob_desejada1=0.95

df1=9
df2=9  

f_desejado1=round(qf(prob_desejada1,df1, df2), 4)
d_desejada1=df(f_desejado1,df1, df2)

f_calculado=22.056
d_calculada=df(f_calculado,df1, df2)


f_test_4=ggplot(data.frame(x = c(0, 25)), aes(x)) +
  stat_function(fun = df,
                geom = "area",
                fill = "lightgrey",
                xlim = c(0,f_desejado1),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  stat_function(fun = df,
                geom = "area",
                fill = "red",
                xlim = c(f_desejado1,25),
                colour="black",
                args = list(
                  df1 = df1,
                  df2 = df2
                ))+
  scale_y_continuous(name="Densidade") +
  #scale_x_continuous(name="Valores score (f)", breaks = c(f_desejado1, f_desejado2))+  
  scale_x_continuous(name="Valores score (f)")+  
  labs(title="Curva da função densidade \nDistribuição F", 
  subtitle = "P(0; 22,056)=(1-\u03b1) em cinza (nível de confiança) \nP(22,056 ; \U221e)= \u03b1 em vermelho (nível de significância) ")+
  geom_segment(aes(x = f_desejado1, y = 0, xend = f_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=f_desejado1+0.1, y=d_desejada1, label="F crítico", angle=90, vjust=0, hjust=0, color="blue",size=4)+
    geom_segment(aes(x = f_calculado, y = 0, xend = f_calculado, yend = d_calculada), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=f_calculado+0.1, y=d_desejada1, label="F calculado", angle=90, vjust=0, hjust=0, color="blue",size=4)+
 annotate(geom="text", x=f_desejado1+5, y=d_desejada1, label="Zona de rejeição \n(para F calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=f_desejado1-2.5, y=d_desejada1, label="Zona de não rejeição  \n(para F calculado)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()

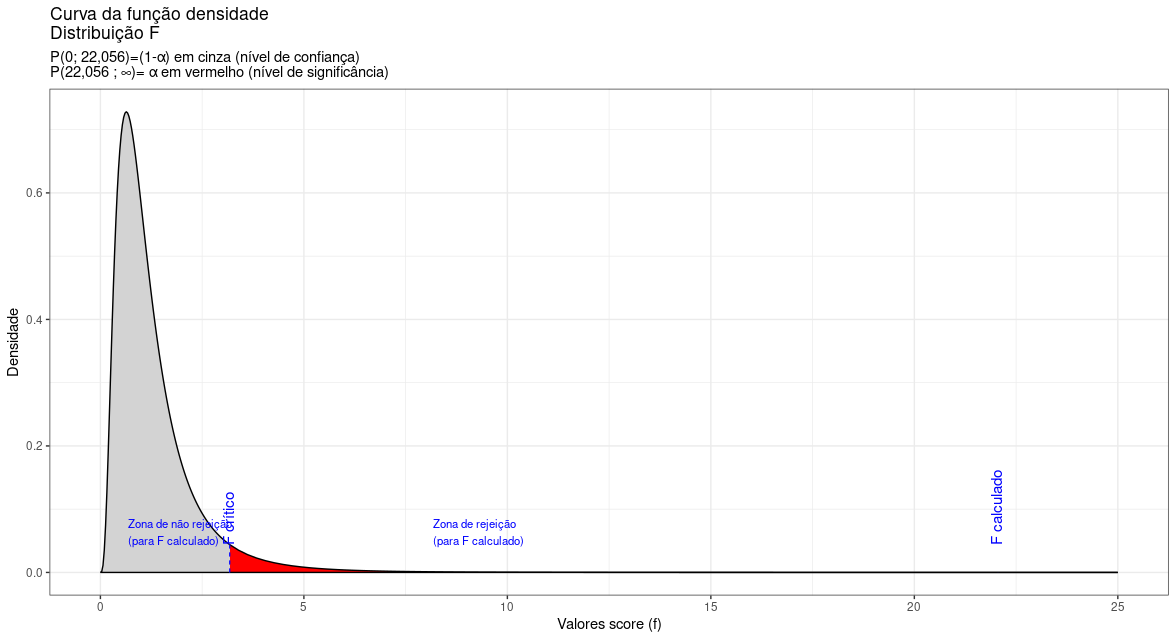
Figure 11.25: O valor calculado da estatística de teste (\(F_{calc}=3,18\)) situa-se na região significante do teste, permitindo a rejeição da hipótese nula de que as variâncias sejam iguais sob o nível de confiança estabelecido.

Conclusão: não se pode aceitar a hipótese de que as variâncias sejam iguais a um nível de significância de 5% (cf. figura 11.25).

Estatística do teste: \(T \sim t_{(\nu)}\) considerando que as variãncias populacionais não podem ser, estatisticamente, admitidas como iguais:

\[ t_{calc} = \frac{(\stackrel{-}{x}_{1} - \stackrel{-}{x}_{2})-\Delta_{0}} { \sqrt{\frac{S^{2}_{1}}{n_{1}}+\frac{S^{2}_{2}}{n_{2}}}} \]

em que:

• \(\mu_{1} , \mu_{2}\) são as médias das populações em teste;
  
• \(\stackrel{-}{x}_{1}=70,90, S_{1}^{2}= 25,339^{2} , n_{1}=10\) são a média, a variância e o tamanho amostral 1;
  
• \(\stackrel{-}{x}_{2}=84, S_{2}^{2}= 5,395^{2} , n_{2}=10\) são a média, a variância e o tamanho amostral 2;
  
• \({t}_{tab \left(\frac{\alpha }{2};\nu \right)}\) ou \({t}_{tab \left(\alpha ;\nu \right)}\): o quantil associado na distribuição ``t’’ de Student ao nível de significância pretendido no teste, com graus de liberdade \((\nu)\).

A aproximação dos graus de liberdade (\(\nu\)) é dada por uma combinação linear das variâncias de amostras independentes (equação de Welch-Satterhwaite, 1946):

\[ \nu=\frac{{\left(\frac{{S}_{1}^{2}}{{n}_{1}}+\frac{{S}_{2}^{2}}{{n}_{2}}\right)}^{2}}{\frac{{\left(\frac{{S}_{1}^{2}}{{n}_{1}}\right)}^{2}}{{n}_{1}-1}+\frac{{\left(\frac{{S}_{2}^{2}}{{n}_{2}}\right)}^{2}}{{n}_{2}-1}}=10 \]

(aproximar o resultado para o inteiro superior mais próximo).

Cálculo da estatística do teste:

\[ t_{calc} = \frac{(\stackrel{-}{x}_{1} - \stackrel{-}{x}_{2})-\Delta_{0}} { \sqrt{\frac{S^{2}_{1}}{n_{1}}+\frac{S^{2}_{2}}{n_{2}}}}=-1,599 \]

Da tabela `t’’ de Student obtemos o valor crítico bicaudal da estatística:

\[ |{t}_{tab \left(\frac{\alpha }{2};\nu \right)}| = |{t}_{tab \left(\frac{0,025}{2};10 \right)}| = 2,22 \]

alfa=0.05

prob_desejada1=alfa/2
df=8
t_desejado1=round(qt(prob_desejada1,df ),df)
d_desejada1=dt(t_desejado1,df)

prob_desejada2=1-alfa/2
df=8
t_desejado2=round(qt(prob_desejada2, df),df)
d_desejada2=dt(t_desejado2,df)

t_calculado=-1.599
d_calculado=dt(t_calculado,df)


ggplot(NULL, aes(c(-4,4))) +
  geom_area(stat = "function", 
            fun = dt,
            args=list(df), 
            fill = "red", 
            xlim = c(-4, t_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(t_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "lightgrey", 
            xlim = c(0, t_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dt, 
            args=list(df), 
            fill = "red", 
            xlim = c(t_desejado2,4),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de t", breaks = c(t_desejado1, t_desejado2))  +
  labs(title= 
         "Regiões críticas sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P(-2,22, 2,22)=(1-\u03b1) em cinza (nível de confiança=0,95) \nP(-\U221e; -2,22)= P(2,22; \U221e)= \u03b1/2 em vermelho (nível de significância/2=0,025) ")+ geom_segment(aes(x = t_desejado1, y = 0, xend = t_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
 geom_segment(aes(x = t_desejado2, y = 0, xend = t_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=t_desejado1-0.1, y=d_desejada1, label="valor crítico=-2,101", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=t_desejado2+0.3, y=d_desejada2, label="valor crítico=2,101", angle=90, vjust=0, hjust=0, color="blue",size=3)+
 annotate(geom="text", x=t_desejado1-2, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
 annotate(geom="text", x=t_desejado2+0.5, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
 annotate(geom="text", x=t_desejado1+2, y=0.2, label="Região de não rejeição da hipótese nula \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
 geom_segment(aes(x = t_calculado, y = 0, xend = t_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
 annotate(geom="text", x=t_calculado-0.1, y=d_calculado, label="valor da estatística do teste=-1,599", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()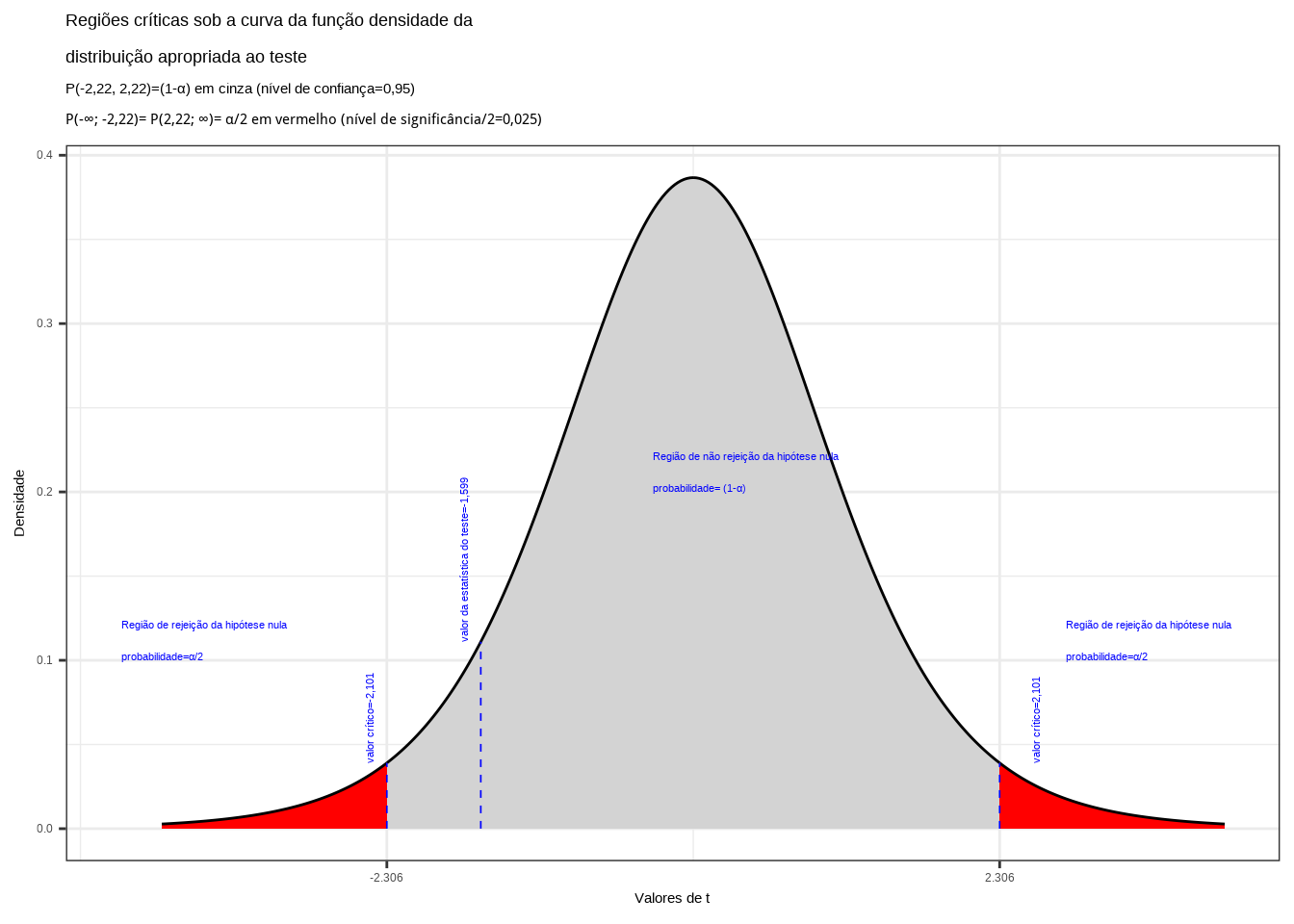

Figure 11.26: Regiões de rejeição da hipótese nula para o teste bilateral (tipo: diferente de) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valores críticos da estatística do teste: \(t_{crit} =\pm 2,22\). O valor calculado da estatística (\(t_{calc}=-1,599\)) não se situa na faixa de significância do teste, não nos permitindo a rejeição da hipótese nula sob aquele nível de confiança

Conclusão: Os resultados obtidos pela análise estatística de comparação de médias das duas amostras colhidas das notas de testes de matemáticas realizados em duas escolas diferentes (1 e 2) não nos permitem rejeitar a hipótese de que suas médias sejam iguais a um nível de confiança de 5% (cf. figura 11.26.