11.10 Teste de uma proporção amostral

A aproximação de uma população sob distribuição Binomial pela distribuição Normal pode ser realizada desde que atendidas às seguintes condições:

a amostra é colhida de modo aleatório, os ensaios são independentes e com probabilidade de ``sucesso’’ constante;
se a amostra é colhida sem reposição, o tamanho da população deve ser ao menos 10 (20) vezes o tamanho da amostra ($N \ge 10,20 \cdot n$);
tamanho de amostra deve ser de ao menos 30 ($n \ge 30$);
a proporção populacional não extrema (próxima a 0 ou 1);
o número de ``sucessos’’ deve ser de ao menos 5 ($n \cdot \pi_{0} \ge 5$); e,
o número de ``fracassos’’ deve ser de ao menos 5 ($n \cdot (1-\pi_{0}) \ge 5$).

11.10.1 Estruturas possíveis para as hipóteses

Teste bilateral (tipo: diferente de)

\[ \begin{cases} H_{0}: \pi = \pi_{0}\\ H_{1}: \pi \ne \pi_{0}\\ \end{cases} \]

Teste unilateral à esquerda (tipo: menor que)

\[ \begin{cases} H_{0}: \pi \ge \pi_{0}\\ H_{1}: \pi < \pi_{0}\\ \end{cases} \]

Teste unilateral à direita (tipo: maior que)

\[ \begin{cases} H_{0}: \pi \le \pi_{0}\\ H_{1}: \pi > \pi_{0}\\ \end{cases} \]

Estatística do teste:

\[ Z=\frac{p-\pi_{0} }{\sqrt{\frac{\pi_{0} \left(1-\pi_{0}) \right)}{n}}} \sim \mathcal{N}(0,1) \]

em que:

onde:

$p$ é a proporção observada na amostra, uma estimativa da proporção populacional $\pi$;
$\pi_{0}$ o valor (desconhecido) inferido à proporção populacional, a ser testado frente à proporção amostral; e,
$n$: é o tamanho da amostra.

11.10.2 Probabilidade dos intervalos de confiança para os testes de hipóteses com o uso da estatística Z ($Z \sim \mathcal{N}(0,1)$):

Teste de hipóteses bilateral (tipo: diferente de):

\[\begin{align*} P[\left|Z_{calc}\right| \le {Z}_{tab\left(\frac{\alpha }{2}\right)}|\pi= \pi_{0}] & =(1-\alpha) \\ P( -{Z}_{tab\left(\frac{\alpha }{2}\right)} \le Z_{calc} \le {Z}_{tab\left(\frac{\alpha }{2}\right)} ) & =(1-\alpha)\\ \end{align*}\]

Teste de hipóteses unilateral à esquerda (tipo: menor que):

\[\begin{align*} P[Z_{calc} \ge {Z}_{tab\left(\alpha \right)}|\pi \ge \pi_{0}] & =(1-\alpha)\\ P( Z_{calc} \ge {Z}_{tab\left(\alpha \right)}) & = (1-\alpha)\\ \end{align*}\]

Teste de hipóteses unilateral à direita (tipo maior que):

\[\begin{align*} P[Z_{calc} \le {Z}_{tab\left(\alpha \right)}|\pi \le \pi_{0}] & =(1-\alpha)\\ P( Z_{calc} \le {Z}_{tab\left(\alpha \right)}) & = (1-\alpha)\\ \end{align*}\]

Nas figuras 11.8, 11.9 e 11.10 observam-se:

as regiões de rejeição da hipótese nula (subdivididas nos dois ou em apenas um dos lados) sob a curva da função densidade de probabilidade da distribuição adequada ao teste com probabilidades iguais ao nível de significância $\alpha$ ;
a região de não rejeição da hipótese nula (delimitada à esquerda e à direita ou apenas em um dos lados) com probabilidade igual ao nível de confiança $(1-\alpha)$; e,
os valores críticos da estatística do teste.

Exemplo: Um relatório de uma companhia afirma que 40% de toda a água obtida a partir de poços artesianos no nordeste é salobra. Há muita controvérsia sobre essa informação, alguns dizem que a proporção é maior, outros que é menor. Para dirimir essa dúvida, 400 poços foram sorteados e observou-se em 120 deles que a água era salobra. Qual seria a conclusão a um nível de significância de 3%?

O problema nos pede um teste bilateral (tipo: diferente de):

\[ \begin{cases} H_{0}: \pi = 0,40\\ H_{1}: \pi \ne 0,40\\ \end{cases} \]

Iremos verificar se a informação amostral obtida nos permite rejeitar a hipótese nula que afirma ser a proporção dos poços com água salobra é de 40%, fazendo então valer a hipótese alternativa que afirma ser diferente de 40%.

Verificação das condições:

nada se afirmou sobre o tamanho da população para se verificar: $N ge 10n$);
tamanho de amostra $n \ge 30$: nossa amostra é de 400 poços;
proporção populacional não extrema (próxima a 0 ou 1): a afirmação é de que $\pi=0,40$; e,
$(n \cdot \pi)$ e $(n \cdot (1-\pi)$ são maiores que 5 (160 e 240, respectivamente).

Assim, a estatística do teste fica definida como sendo:

\[ Z=\frac{p-\pi_{0} }{\sqrt{\frac{\pi_{0} \left(1-\pi_{0}) \right)}{n}}} \sim \mathcal{N}(0,1) \]

em que:

$p=0,30$ é a proporção amostral, uma estimativa da proporção populaciona $\pi$;
$\pi_{0}=0,40$ é o valor (desconhecido) inferido à proporção populacional, a ser testado frente à proporção amostral; e,
$n=400$: é o tamanho da amostra.

Da tabela da distribuição Normal padronizada obtemos o valor crítico bicaudal: $|{Z}_{tab\left(\frac{\alpha }{2}\right)}|=2,17$. Pelo cálculo, a estatística do teste é $z_{calc}=-4,082$.

alfa=0.03

prob_desejada1=alfa/2
z_desejado1=round(qnorm(prob_desejada1),4)
d_desejada1=dnorm(z_desejado1, 0, 1)

prob_desejada2=1-alfa/2
z_desejado2=round(qnorm(prob_desejada2),4)
d_desejada2=dnorm(z_desejado2, 0, 1)

z_calculado=-4.082
d_calculado=dnorm(z_calculado, 0, 1)


ggplot(NULL, aes(c(-5,5))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-5, z_desejado1),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado1,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado2),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado2,5),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de z", breaks = c(z_desejado1,z_desejado2))  +
  labs(title= 
         "Regiões críticas sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P(-2,17, 2,17)=(1-\u03b1) em cinza (nível de confiança=0,97) \nP(-\U221e; -2,17)= P(2,17; \U221e)= \u03b1/2 em vermelho (nível de significância/2=0,015) ")+
  geom_segment(aes(x = z_desejado1, y = 0, xend = z_desejado1, yend = d_desejada1), color="blue", lty=2, lwd=0.3)+
  geom_segment(aes(x = z_desejado2, y = 0, xend = z_desejado2, yend = d_desejada2), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_desejado1-0.1, y=d_desejada1, label="valor crítico=-2,17", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.3, y=d_desejada2, label="valor crítico=2,17", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1-1.5, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado2+0.5, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1/2", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  annotate(geom="text", x=z_desejado1+1.3, y=0.2, label="Região de não rejeição da hipótese nula \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  geom_segment(aes(x = z_calculado, y = 0, xend = z_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_calculado-0.1, y=d_calculado, label="valor da estatística do teste=-4,082", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()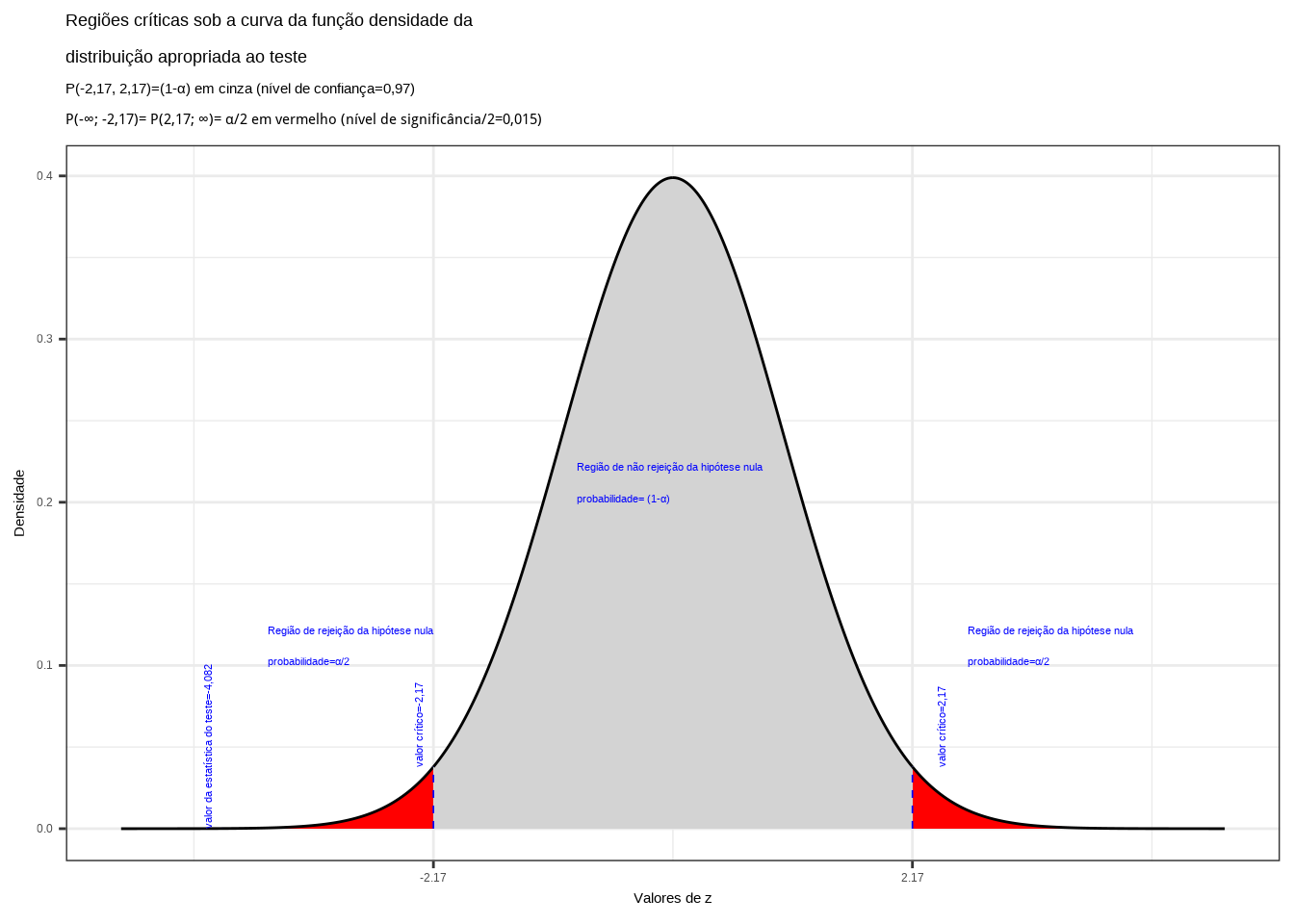

$Regiões de rejeição da hipótese nula para o teste bilateral (tipo: diferente de) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valores críticos da estatística do teste: $z_{crit} =\pm 2,17$. O valor calculado da estatística ($z_{calc}=-4,082$) situa-se na faixa de significância do teste, possibilitando a rejeição da hipótese nula sob aquele nível de confiança$

Figure 11.27: Regiões de rejeição da hipótese nula para o teste bilateral (tipo: diferente de) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valores críticos da estatística do teste: $z_{crit} =\pm 2,17$. O valor calculado da estatística ($z_{calc}=-4,082$) situa-se na faixa de significância do teste, possibilitando a rejeição da hipótese nula sob aquele nível de confiança

Conclusão: Os resultados obtidos na análise estatística realizada nos permitem rejeitar a hipótese de que a proporção de poços com água salobra é de 40% sob um nível de confiança de 97%. A proporção de poços com água salobra no Nordeste é diferente de 40% (Figura 11.25).

Teste unilateral à esquerda (tipo: menor que)

\[ \begin{cases} H_{0}: \pi \ge 0,40\\ H_{1}: \pi < 0,40\\ \end{cases} \]

Iremos verificar se a informação amostral obtida nos permite rejeitar a hipótese nula que afirma ser a proporção igual ou maior a 40%, fazendo então valer a hipótese alternativa que afirma ser a proporção menor que 40%.

Da tabela obtemos o valor crítico monocaudal: $Z_{tab\left(\alpha\right)}=-1,88$. Pelo cálculo, a estatística do teste é $Z_{calc}=-4,082$.

alfa=0.03
prob_desejada=alfa
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)

z_calculado=-4.082
d_calculado=dnorm(z_calculado, 0, 1)




ggplot(NULL, aes(c(-5,5))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(-5, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado,0),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(0, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(z_desejado,5),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de z", breaks = c(z_desejado))  +
  labs(title= 
         "Região crítica sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P( -1,88,\U221e,)=(1-\u03b1) em cinza (nível de confiança=0,97) \nP(-\U221e; -1,88)=\u03b1 em vermelho (nível de significância=0,03) ")+
geom_segment(aes(x = z_desejado, y = 0, xend = z_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
annotate(geom="text", x=z_desejado-0.1, y=d_desejada, label="valor crítico=-1,88", angle=90, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado-2, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1", angle=0, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado+1, y=0.2, label="Região de não rejeição da hipótese nula  \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  geom_segment(aes(x = z_calculado, y = 0, xend = z_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_calculado-0.1, y=d_calculado, label="valor da estatística do teste=-4,082", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()

$Regiões de rejeição da hipótese nula para o teste unilateral à esquerda (tipo: menor que) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valor crítico da estatística do teste: $z_{crit} = -1,88$. O valor calculado da estatística ($z_{calc}=-4,082$) situa-se na faixa de significância do teste, o que nos permite a rejeição da hipótese nula sob aquele nível de confiança$

Figure 11.28: Regiões de rejeição da hipótese nula para o teste unilateral à esquerda (tipo: menor que) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelos valor crítico da estatística do teste: $z_{crit} = -1,88$. O valor calculado da estatística ($z_{calc}=-4,082$) situa-se na faixa de significância do teste, o que nos permite a rejeição da hipótese nula sob aquele nível de confiança

Teste unilateral à direita (tipo: maior que)

\[ \begin{cases} H_{0}: \pi \le 0,40\\ H_{1}: \pi > 0,40\\ \end{cases} \]

Iremos verificar se a informação amostral obtida nos permite rejeitar a hipótese nula que afirma ser a proporção igual ou meor a 40%, fazendo então valer a hipótese alternativa que afirma ser a proporção maior que 40%.

Da tabela obtemos o valor crítico monocaudal: $Z_{tab\left(\alpha\right)}=1,88$. Pelo cálculo, a estatística do teste é $Z_{calc}=-4,082$.

alfa=0.97
prob_desejada=alfa
z_desejado=round(qnorm(prob_desejada),4)
d_desejada=dnorm(z_desejado, 0, 1)

z_calculado=-4.082
d_calculado=dnorm(z_calculado, 0, 1)




ggplot(NULL, aes(c(-5,5))) +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "lightgrey", 
            xlim = c(-5, z_desejado),
            colour="black") +
  geom_area(stat = "function", 
            fun = dnorm, 
            fill = "red", 
            xlim = c(z_desejado,5),
            colour="black") +
  scale_y_continuous(name="Densidade") +
  scale_x_continuous(name="Valores de z", breaks = c(z_desejado))  +
  labs(title= 
         "Região crítica sob a curva da função densidade da \ndistribuição apropriada ao teste", 
       subtitle = "P( -\U221e; 1,88)=(1-\u03b1) em cinza (nível de confiança=0,97) \nP(1,88; \U221e)=\u03b1 em vermelho (nível de significância=0,03) ")+
geom_segment(aes(x = z_desejado, y = 0, xend = z_desejado, yend = d_desejada), color="blue", lty=2, lwd=0.3)+
annotate(geom="text", x=z_desejado-0.1, y=d_desejada, label="valor crítico=-1,88", angle=90, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado+1, y=0.1, label="Região de rejeição da hipótese nula \nprobabilidade=\u03b1", angle=0, vjust=0, hjust=0, color="blue",size=3)+
annotate(geom="text", x=z_desejado-2.5, y=0.2, label="Região de não rejeição da hipótese nula  \nprobabilidade= (1-\u03b1)", angle=0, vjust=0, hjust=0, color="blue",size=3)+
  geom_segment(aes(x = z_calculado, y = 0, xend = z_calculado, yend = d_calculado), color="blue", lty=2, lwd=0.3)+
  annotate(geom="text", x=z_calculado-0.1, y=d_calculado, label="valor da estatística do teste=-4,082", angle=90, vjust=0, hjust=0, color="blue",size=3)+
  theme_bw()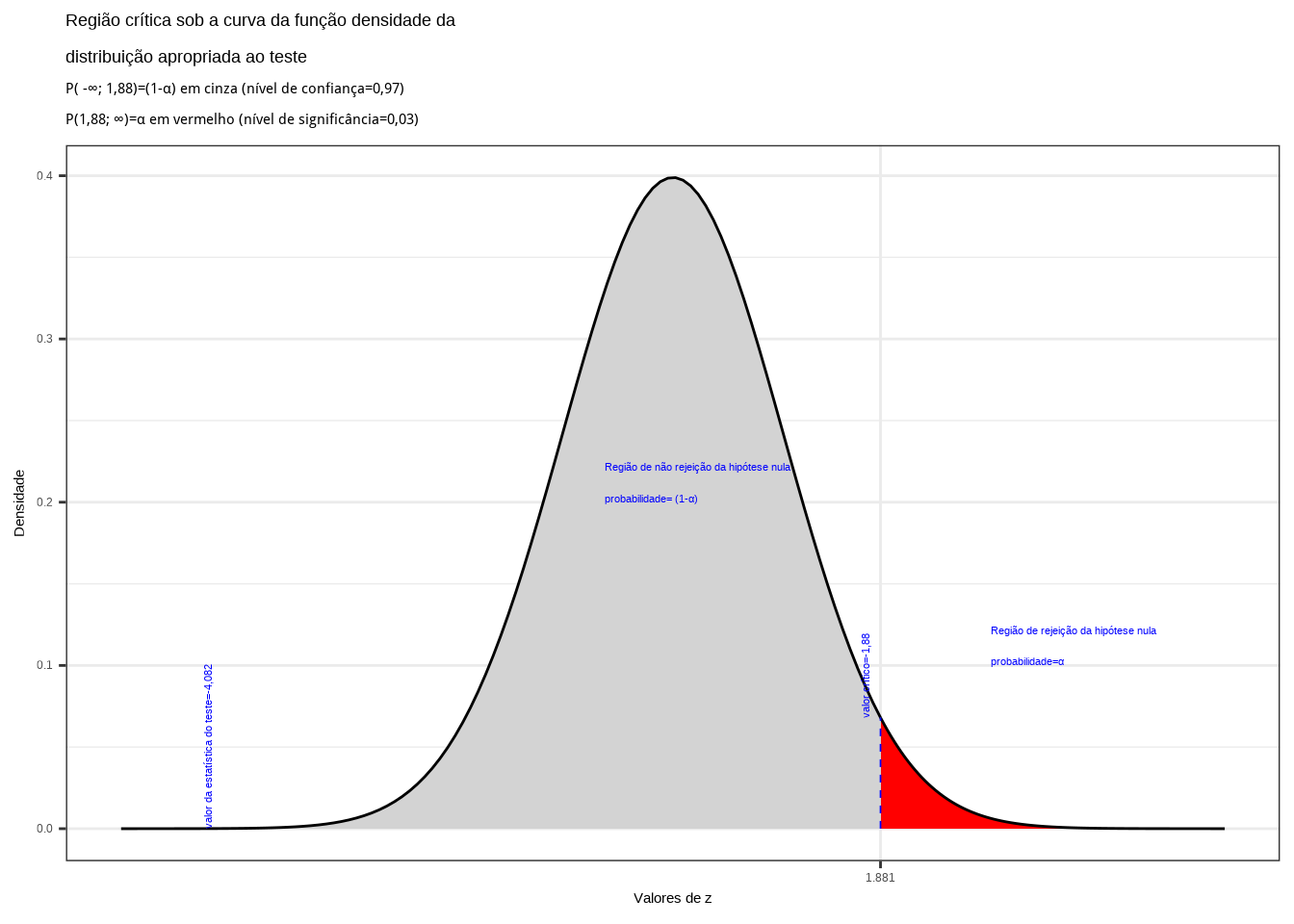

$Região de rejeição da hipótese nula para o teste unilateral à direita (tipo: maior que) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $z_{crit} = 1,88$. O valor calculado da estatística ($z_{calc}=-4,082$) situa-se na faixa de não significância do teste, não possibilitando a rejeição da hipótese nula sob aquele nível de confiança$

Figure 11.29: Região de rejeição da hipótese nula para o teste unilateral à direita (tipo: maior que) realizado: a região de não rejeição da hipótese nula (região de não significância do teste) está delimitada pelo valor crítico da estatística do teste: $z_{crit} = 1,88$. O valor calculado da estatística ($z_{calc}=-4,082$) situa-se na faixa de não significância do teste, não possibilitando a rejeição da hipótese nula sob aquele nível de confiança

Conclusão: Os resultados obtidos na análise estatística realizada não nos permitem rejeitar a hipótese de que a proporção de poços com água salobra seja menor ou igual a 40% sob um nível de confiança de 97%. (cf. Figura 11.27).

UNIVERSIDADE ESTADUAL DE LONDRINA
CCE - Centro de Ciências Exatas
DSTA - Departamento de Estatística (sala 11)
Prof. M.e Eng.\(^{o}\) Felinto Junior Da Costa
fjcosta@uel.br

11.10 Teste de uma proporção amostral

11.10.1 Estruturas possíveis para as hipóteses

11.10.2 Probabilidade dos intervalos de confiança para os testes de hipóteses com o uso da estatística Z (\(Z \sim \mathcal{N}(0,1)\)):